一种基于共轭梯度法的广义单隐层神经网络
孙 峰,龚晓玲,张炳杰,柳毓松,王延江
(中国石油大学(华东), 山东 青岛 266580)
0 引言
人工神经网络是一种模仿人脑神经元的结构和信息传递过程所建立的数学模型,具有学习、记忆等功能.近三十年来神经网络得到迅速的发展并在模式识别等领域有着广泛的应用,尤其在未来智能化城市发展中会起到关键作用.其中,应用最广泛的就是采用了反向传播(back propagation)学习算法[1]的前馈神经网络,这种网络也称为BP神经网络,自1986年被提出之后,至今仍在神经网络中占据重要地位.该网络在训练时信息从前向后逐层传播,而网络中的权重则通过误差反向传播来调整.这种算法结构简单且能够以任意精度逼近任意非线性函数[2-3],但也存在一些缺陷:由于网络收敛速度慢,导致训练花费时间过长;由于采用梯度下降法易陷入局部极小值;易过拟合训练使其泛化能力变差等.
为了加快网络的训练速度,黄广斌等提出了一种针对单隐层前馈神经网络的快速构建与学习算法[4],因其快速特性而称之为超限学习机(extreme learning machine, ELM).ELM算法的整个学习过程一次完成,使得网络训练大大简化,运算速度几十倍甚至几千倍于BP算法[5-6],ELM在许多领域都取得了突出成果[7-9].虽然网络训练效果很好,但ELM相对于传统的神经网络,需要更多的隐层节点才能达到同样的训练精度[10].由于使用大量隐层节点,计算工作量会大大增加,特别是样本超高维时,测试速度明显变慢;过多的隐层节点也会使网络过拟合而降低泛化能力.
针对ELM存在的问题,文献[11]提出了用梯度下降法来选择合适权值的upper-layer-solution-aware(USA)算法.使用最速下降法来更新从输入层到隐层的权值.它与传统的神经网络的区别在于是用广义逆一步得出,相当于传统BP算法和ELM算法的结合.与BP神经网络相比,它的速度大大提高了;与ELM算法相比,它需要的隐层节点数减少了.相比于ELM,它在训练上需要浪费一些时间,但是实际应用中,往往测试时间比训练时间更加关键,减少隐层节点数,有利于缩短测试时间,更符合实际工程需要.
笔者借鉴ELM的一次学习思想,提出了一种基于共轭梯度法的快速学习算法,由于共轭梯度法计算复杂度不高于最速下降法,但是收敛速度优于最速下降法,使得笔者算法在保持快速这一优势前提下,网络训练精度得到进一步提高.
1 ELM和USA算法描述
在介绍笔者算法前,先简单介绍一下ELM的基本算法以及ELM算法和BP算法相结合的USA算法.这两种算法都应用于单隐层前馈神经网络且有良好的数值表现,ELM算法随机赋予输入层到隐层的权值,无需迭代,因此训练时间极快.USA算法用最速下降法对输入层到隐层的权值进行优化,虽训练时间稍慢,但达到相同网络训练精度所需隐层节点个数要大大少于ELM.
1.1 超限学习机

(1)
式中:wi=[wi1,wi2,…,win]T为连接输入层到隐层第i个单元之间的权值;ui=[ui1,ui2,…,uin]T为连接隐层第i个单元到输出层之间的权值;bi为第i个隐节点的阈值.
如果这个网络可以零误差地学习这N个样本,即
(2)
上式表示成矩阵的形式为:
HU=T,
(3)
式中:H为隐层输出矩阵[12-13].
(4)

U=H-1T,
(5)

U=H†T,
(6)
式中:H†=(HTH)-1HT.
通过以上原理,可以看出ELM最大的优点在于它无需迭代,一步就能求出隐层权值U.
1.2 最速下降法
USA算法是文献[11]中提出的一种算法.下面简单介绍其原理.
(7)
然后沿负梯度方向优化W,即
(8)
式中:η为学习率.
这样在每次迭代后只优化更新连接输入层和隐藏层的权值W,使误差逐步减小,达到可接受误差或最大迭代次数时迭代结束,得到了优化的网络结构.
2 笔者工作
要想降低网络的隐层节点个数,一种有效方法就是对其权值进行优化.从最优化原理来说,优化权值的方法有最速下降法、共轭梯度法、牛顿法等.BP算法就是采用最速下降法达到优化权值的目的.
2.1 共轭梯度法
共轭梯度法是一类效果较好的共轭方向法,最早由Hestenes和Stiefel提出并用于求解线性方程组[14],后来被Fletcher和Reeves引入求解无约束最优化问题[15].共轭梯度法的原理是:在寻优过程中,利用当前点xk处的梯度向量g(xk)和前一迭代点xk-1处的搜索方向dk-1对最速下降方向进行如下修正:
dk=-g(xk)+βkdk-1,
(9)
并保证新的搜索方向dk与之前的搜索方向dk-1,dk-2,…,d0之间满足共轭关系.其中,修正系数βk的不同又进一步形成了不同的共轭梯度法.
共轭梯度法与最速下降法同样用到一阶导数信息,但它克服了梯度下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点.其优点是所需存储量小,具有有限步收敛性,稳定性高,而且不需要任何外来参数.
2.2 笔者算法

(10)
隐层到输出层间的权值矩阵为:
(11)
那么该网络的隐层输出矩阵为:
H=g(WTX),
(12)
式中:g(·)为隐层激活函数,一般选用Sigmoid函数.根据输出值是否包含负值,分为Log-Sigmoid函数和Tan-Sigmoid函数,本算法选用函数值在0~1的简单Log-Sigmoid函数,即
(13)
网络的输出层激活函数为简单线性函数,则网络的实际输出为:
Y=UTH.
(14)
对于确定网络的权值U,可以将网络结构看成一个线性系统,
UTH=T.
(15)

U=(HT)†TT=(HHT)-1HTT.
(16)
由于H=g(WTX),所以隐层到输出层的权值U可以看作是输入层到隐层的权值W的函数.本算法采用共轭梯度法来对输入层到隐层之间的权值W进行优化.网络的误差函数可以定义为:
(17)
首先求误差函数的梯度,由式(14)和式(17)得:
(18)
再将式(16)带入式(18),得到梯度的计算公式为:
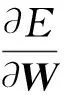
=2X[HTo(I-H)To[H†(HTT)(TH†-TT(TH†))]],
(19)
式中:
H†=HT(HHT)-1.
(20)
本算法采用F-R共轭梯度法,搜索方向为:
(21)
式中:gk即为第k次迭代的梯度,修正项系数为:
(22)
从输入层到隐层的权值W的更新公式为:
Wk+1=Wk+ηkdk,
(23)
式中:学习率ηk通过线搜索的方式获得.
3 数值试验
将笔者提出的算法与USA算法[11]、ELM算法[4]在3种数据库上进行实数值试验,验证算法效果.为了公平评判算法的性能,网络的初始权值均相同,并重复选取不同的随机初始权值进行10次试验,从训练及测试误差(函数拟合)或精度(分类)、训练时间几个方面来评价试验结果(结果为平均值).因为测试时间仅与隐藏层节点数有关,与算法无关,所以在这里不做比较.
3.1 数据库介绍
Sin C函数表达式为:
(24)
Sin C数据的产生方法为在(-10,10)内随机产生5 000组训练样本和5 000组测试样本.通过网络在训练集及测试集上的误差可以衡量网络的学习能力.
MNIST手写数字数据库也是一种衡量分类算法性能的数据库,它源于美国国家标准与技术局收集的NIST数据库,数字图像已被标准化为一张28×28的图片.该数据库以矩阵的形式存放,其中每个样本即每个手写数字都是一个1×784的向量,向量中的每个元素都是0~255的数字,代表的是该像素点的灰度值.MNIST数据库一共有60 000个训练样本和10 000个测试样本.
3.2 试验结果
在Sin C数据库上的试验选取网络的隐层节点数为30,在Diabetes数据库上的试验选取网络的隐层节点数为150,在这两个数据库上USA和笔者算法的迭代次数为10次.训练及测试结果见表1和表2.可以看出,ELM算法训练时间最短,符合ELM算法原理.笔者算法在训练时间与USA 算法相当的情况下,训练及测试误差是3种算法中最小的,精度是3种算法中最高的.
由于MNIST数据库较大,分别选取隐层节点个数为:64、128、256、512、1 024进行试验,计算相应的分类精度.USA和笔者算法的迭代次数为15次.训练及测试结果见表3.可以看出在时间上本算法虽然没有优势,但是精度相比于其他两种算法有所提高.
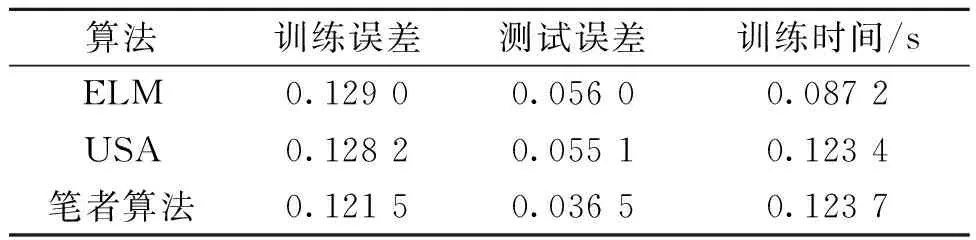
表1 不同算法在Sin C数据库上的误差比较
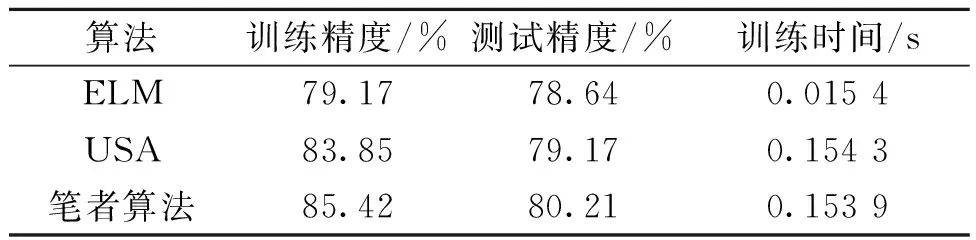
表2 不同算法在Diabetes数据库上的精度比较
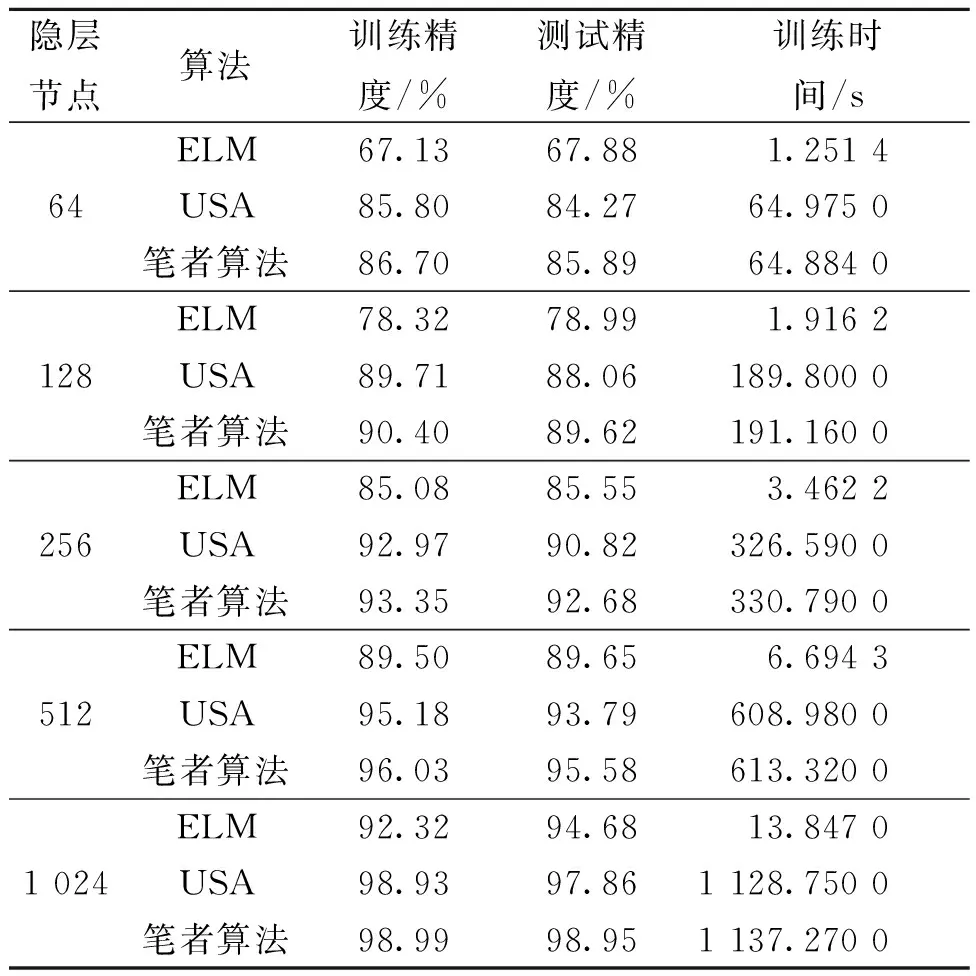
表3 不同算法在MNIST数据库上的误差比较
从表3中一方面可以看出,若要达到相同的测试精度,如90%,ELM大约需要512个隐节点,USA算法大约需要128个隐节点,而笔者算法大约需要90个隐层节点.说明笔者算法在保证相同精度的前提下,可有效地减少了隐层节点数,简化了网络结构,增强了网络的泛化能力.另一方面,对于相同的隐层节点个数,ELM、USA和笔者算法的测试精度依次增高,且USA算法和笔者算法的精度均明显高于ELM算法.说明笔者算法在保证训练时间不是太长的情况下,有效地优化了初始权值,使网络在相同的隐层节点个数下,得到更高的训练精度.
4 结论
针对前馈神经网络中传统算法所需时间过长,而ELM算法所需要的隐层节点数过多的缺陷,笔者算法在保证算法训练速度的前提下,有效提高了网络的精度和泛化能力.从各类数据库的试验可以证明,笔者算法是一个更有效的单隐层前馈神经网络学习算法.
参考文献:
[1]WERBOS P J. Beyond regression: new tools for prediction and analysis in the behavioral sciences[D]. Harvard University, Cambridge,1974.
[2]HORNIK K. Approximation capabilities of multilayer feedforward networks[J]. Neural networks,1991, 4 (2): 251-257
[3]LESHNO M, LIN V Y, PINKUS A, et al. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function[J]. Neural networks, 1993, 6 (6): 861-867.
[4]HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(123): 489-501.
[5]BARTLETT P L. The sample complexity of pattern classification with neural networks: the size of the weights is more important than the size of the network[J]. IEEE trans. Inf. theory, 1998, 44 (2): 525-536.
[6]WIDROW B, GREENBLATT A, KIM Y, et al. The No-Prop algorithm: a new learning algorithm for multilayer neural networks[J]. Neural networks, 2013(37): 182-188.
[7]郝向东, 毛晓波, 梁静. ELM与Mean Shift相结合的抗遮挡目标跟踪算法[J]. 郑州大学学报(工学版), 2016, 37(1):1-5.
[8]王杰, 苌群康, 彭金柱. 极限学习机优化及其拟合性分析[J]. 郑州大学学报(工学版), 2016, 37(2):20-24.
[9]邓万宇, 李力, 牛慧娟. 基于Spark的并行极速神经网络[J]. 郑州大学学报(工学版), 2016, 37(5):47-56.
[10] ZHU Q Y, QIN A K, SUGANTHAN P N, et al. Evolutionary extreme learning machine[J]. Pattern recognition, 2005, 38(10): 1759-1763.
[11] YU D, DENG L. Efficient and effective algorithms for training single-hidden-layer neural networks[J]. Pattern recognition letters, 2012, 33(5):554-558.
[12] HUANG G B, BABRI H A. Upper bounds on the number of hidden neurons in feedforward networks with arbitrary bounded nonlinear activation functions[J]. IEEE transactions on neural networks,1998, 9 (1): 224-229.
[13] HUANG G B. Learning capability and storage capacity of two hidden-layer feedforward networks[J]. IEEE transactions on neural networks, 2003, 14 (2): 274-281.
[14] ARMIJO L. Minimization of functions having Lipschitz continuous first partial derivatives[J]. Pacific journal of mathematics, 1966(16):1-3.
[15] GOLDSTEIN A. On steepest descent[J]. SIAM journal on control, 1965(3):147-151.

