一种自适应确定隐层节点数的增量半监督超限学习机算法

梅 颖，沈 洋，叶思语，卢诚波

(1.丽水学院 工学院，浙江 丽水 323000; 2.温州医科大学 公共卫生与管理学院，浙江 温州 325035)

1 研究背景

随着信息技术的高速发展，人类采集信息、利用数据的能力得到了大幅度地提高。对得到的数据进行挖掘，搜索隐藏于其中的信息，获取有价值的信息和知识，是众多应用领域的共同需求。通常，收集到的数据样本分为标记样本和未标记样本，“标记”指的是数据样本对应的输出，例如，在回归问题中，“标记”通常指的是数据样本的输出值，在分类问题中，“标记”通常指的是数据样本的类标签。目前的学习算法中更多的是利用标记样本进行训练，实际上，收集到的数据样本中，往往是标记样本和未标记样本并存，甚至多是未标记样本占多数的，未标记样本通常需要使用特殊设备或经过不菲且非常耗时的人工标记才能转换为标记样本。例如，在人工智能辅助诊断肺结节的应用中，可以从医疗数据库中获得海量的肺部影像资料作为训练样本，但受人力和物力的限制，无法人工将所有的结节一一标记出来。在许多应用中，未标记样本往往大量存在，其获取成本也相对较低，这些未被标记的数据样本仍然含有有价值的信息，对于辅助学习有很大的帮助。目前，利用未标记样本进行学习的算法主要分为半监督学习、直推学习、生成式模型等学习方法。这些方法的出发点都是利用未标记样本辅助标记样本进行学习，具体思路各不相同，作为解决这一问题的关键技术，半监督学习受到了国际机器学习和数据挖掘领域的研究人员的高度重视，近年来，基于分歧方法的半监督学习[1]、半监督支持向量机[2]、图半监督学习[3]中的代表性论文先后获得代表机器学习学术界最高水平的“国际机器学习大会(International Conference on Machine Learning, ICML)”的“十年最佳论文”奖[4]。Belkin等[5]将流形正则化引入半监督学习的框架中，直接基于局部光滑性假设对定义在标记样本上的损失函数进行正则化，使学得的预测函数具有局部光滑性[4]。Huang等[6]将流形正则化引入超限学习机(Extreme Learning Machine, ELM)[7]的框架中，设计了一种称为“半监督超限学习机(Semi-Supervised ELM, SS-ELM)”的学习方法，利用未标记样本辅助提升了超限学习机的泛化性能。然而，半监督超限学习机仍然需要解决如下的问题: 1) 如何自适应确定合理的隐层节点个数；2) 当隐层节点数增加后，如何重新训练网络。本文基于流形正则化，在半监督超限学习机的基础上，提出了一种增量半监督超限学习机(Incremental SS-ELM, ISS-ELM)算法。对于给定的学习精度，该算法能够逐个或者成批地增加隐层节点，并自适应确定隐层节点数量。在此过程当中，网络的外权矩阵不需要重新训练，只需逐步更新，当隐层节点数较大时，能大幅减少半监督超限学习机的训练时间。

2 相关工作

本文在超限学习机和半监督超限学习机的基础上提出了一种增量半监督超限学习机算法，下文先简单介绍超限学习机和半监督超限学习机。

超限学习机是一种单隐层前馈网络学习算法，网络的内权和隐层偏置随机给定，外权通过解优化问题得到，具有学习速度快、人工干预少且泛化性能好等特点。

超限学习机中，训练样本x的隐层输出表示为一个行向量

h(x)=[G(a1,b1,x),G(a2,b2,x),…,G(ak,bk,x)]。

(1)

式中:aj,bj(j=1,2,…,k)为随机给出的第j个隐层节点对应的学习参数；k为隐层节点个数；G(x)为激励函数。给定N个训练样本(xi,ti)，xi∈m,ti∈n，超限学习机的数学模型为

Hβ=T。

(2)

式中:H为隐层输出矩阵，且

(3)

β为外权矩阵；T为目标矩阵。该模型的解为

(4)

为了提高学习器的泛化性能，Deng等[8]给出了该模型的岭回归版本:

Subject toHβ=T-ε。

(5)

(6)

式中:c为参数；I为单位矩阵。

半监督超限学习机的学习过程如下[6]:

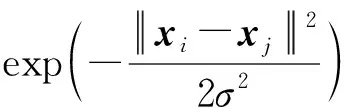
通过解如下优化问题确定半监督超限学习机的外权矩阵β:

(7)

上述优化问题的解为

(8)

式中：Ik为k阶单位矩阵。

3 ISS-ELM算法

对于给定的l个标记样本和u个未标记样本，设初始隐层节点个数为k0，初始隐层输出矩阵为H0，考虑式(8)中l>k的情形(l≤k的情形类似可得)，则初始外权矩阵

(9)

当增加δ0=k1-k0个隐层节点时，

(10)

则Ik0+H0T(C+λL)H0的Schur补为

P(P=(Iδ0+ΔH0T(C+λL)ΔH0)-ΔH0T(C+λL)H0(Ik0+H0T(C+λL)H0)-1H0T(C+λL)ΔH0)。

选取适当的参数λ，使得矩阵P可逆，由2×2块矩阵的逆矩阵表达式[9]可得

将上式代入式(10)可得

(11)

特别地，当λ=0时，式(11)退化为文献[10]中的“隐层节点增加和增量学习的最小化误差的超限学习机”(Error Minimized Extreme Learning Machine with growth of hidden nodes and incremental learning, EM-ELM)，即无未标记样本的增量算法。

为避免重复计算，式(11)中的Q0,R0,U0,V0可按照以下顺序计算:

①P-1(ΔH0T(C+λL)H0)→P-1(ΔH0T(C+λL)H0)β0(=U0);

② (Ik0+H0T(C+λL)H0)-1(H0T(C+λL)ΔH0)→(Ik0+H0T(C+λL)H0)-1(H0T(C+λL)ΔH0)U0(=Q0);

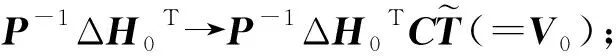
④ (Ik0+H0T(C+λL)H0)-1(H0T(C+λL)ΔH0)V0(=R0)。

利用式(11)，我们给出增量半监督超限学习机(ISS-ELM)算法:

输出:β

阶段1: 初始阶段

ⅰ) 对于给定的l个标记样本和u个未标记样本，确定初始隐层节点个数为k0，随机给定第j个隐层节点的学习参数aj和bj(j=1,2,…,k0)；

ⅱ) 计算初始隐层输出矩阵

ⅲ) 利用式(9)计算初始外权矩阵β0；

ⅴ) 设i=0。

阶段2: 隐层节点增长阶段

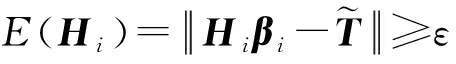
ⅰ)i=i+1;

ⅱ) 增加δi-1个隐层节点，隐层节点总数为ki个，随机给定第j个隐层节点的学习参数aj和bj(j=k0+1,k0+2,…,k1)，相应的隐层输出矩阵Hi+1=[Hi,ΔHi]，

ⅲ) 外权矩阵β调整为

(12)

返回阶段2。

4 仿真实验

4.1 数据集信息

本节选用9个在机器学习当中经常出现的数据集作为测试数据集，其中1个为人工数据集“SinC”，另外8个为实际问题的数据集(4个用作回归，4个用作分类)，用来评估半监督超限学习机(SS-ELM)算法、无未标记样本的增量超限学习机(EM-ELM)算法与增量半监督超限学习机(ISS-ELM)算法的性能。数据集的具体信息见表1。数据集采用5-折交叉验证，每次实验从训练集中随机挑选10%的样本作为有标记样本，其余为无标记样本。运行30次，实验结果取平均值。回归问题用测试集上的均方根误差(Root Mean Square Error, RMSE)ERMS来度量，分类问题用测试集上的分类精确度λACC来度量。

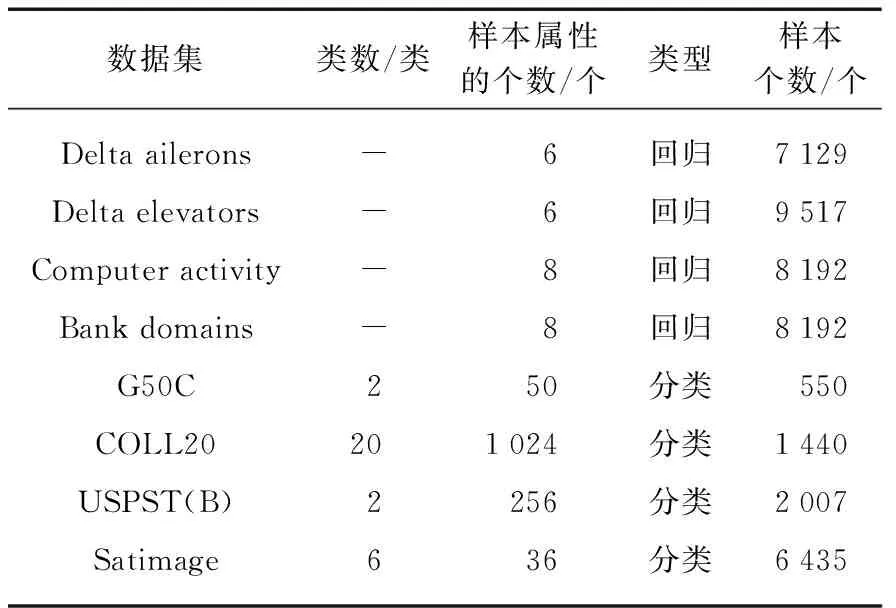
表1 实验数据集细节

人工数据集“SinC”的表达式:

数据产生方法: 在区间(-10，10)内随机生成10 000个样本，在训练样本上加取值范围为[-0.2,0.2]的随机噪声，测试样本不加噪声。

4.2 实验设置

对于人工数据集“SinC”，初始隐层节点个数设为5，每次增加1个隐层节点，增加至30个隐层节点。其他数据集的实验中: 对于回归问题，训练集的目标均方根误差设置为0.01，最大隐层节点个数设置为300；对于分类问题，训练集的目标分类精度设置为90%，最大隐层节点个数设置为300。

实验中激励函数采用sigmoid函数。使用的仿真软件为Matlab R2018b，实验的环境为Window 10 64bit操作系统，Intel Core i7-6700，CPU主频为3.40 GHz，16 GB内存。

4.3 实验结果

图1给出了“SinC”数据集上SS-ELM、EM-ELM与ISS-ELM3种学习机的均方根误差的结果。从图1中可以看出，由于未标记样本的辅助学习，ISS-ELM与SS-ELM比EM-ELM具有更好的泛化性能。图2对“SinC”数据集上SS-ELM、EM-ELM与ISS-ELM3种学习机的训练时间进行了比较。可以看出，SS-ELM的训练时间最长，并且随着隐层节点个数的增加，训练时间随之增加，这是由于SS-ELM在每次增加新的隐层节点时，没能利用旧的外权矩阵构造新的外权矩阵，而是完全重新计算外权矩阵，导致训练时间增加。与之不同的是，EM-ELM和ISS-ELM只是对旧的外权矩阵进行了部分更新和替换，因此训练时间要少得多。另外，由于ISS-ELM使用了未标记样本进行辅助学习，所以训练时间要略多于EM-ELM的训练时间，但考虑到ISS-ELM泛化能力上的优势，综合分析，在“SinC”这个数据集的实验中，ISS-ELM算法的表现最好。

图1 算法在SinC上的均方根误差Fig.1 RMSE of the algorithm on SinC

图2 算法在SinC上的训练时间Fig.2 Training time of the algorithm on SinC

从表2中可以发现，在这3种学习机中，EM-ELM由于没有利用未标记样本进行辅助学习，因此达到相同的训练均方根误差或分类精度经常需要更多的隐层节点，导致网络的规模变大。而ISS-ELM与SS-ELM所需的隐层节点个数相似，但ISS-ELM的优势是可以通过迭代的方法确定最优的隐层节点个数，从而控制网络的规模。

表2 3种方法在测试集上的均方根误差/精确度、隐层节点个数的比较

5 结 语

本文在半监督超限学习机的基础上，提出了一种简单高效的增量半监督超限学习机算法，该算法利用未标记样本进行辅助学习，并且能够自适应确定最优的隐层节点个数，从而得以控制网络规模；同时，在增加隐层节点的过程中，单隐层前馈网络中的外权矩阵不需要重新计算，只需要作局部调整就可以得到新的外权矩阵，加快了学习速度。