强规划的最小期望权值求解算法∗
袁 润 文中华 戴良伟 陈秋茹
(1.湘潭大学信息工程学院 湘潭 411105)(2.湖南工程学院湖南省风电装备与电能变换协同创新中心 湘潭 411104)(3.湘潭大学智能计算与信息处理教育部重点实验室 湘潭 411105)
1 引言
智能规划是人工智能近年来研究的一个重要领域[1~2]。随着人工智能的快速发展,智能规划中的不确定规划问题逐渐成为国内外学者的研究热点[3]。目前,对不确定规划问题的研究在国内外都取得了许多的研究进展[4~5]。最初,Cimatti等在文献[6]给出了不确定规划问题的强规划解,弱规划解和强循环规划解的定义以及说明,并提出用模型检验的方法来求解强规划问题。之后,也有学者提出利用模式识别技术求弱、强、强循环规划解[7],具体地通过反向搜索算法求强规划解,但其不足在于,搜索过程由于缺少引导信息,进行了大量的无用搜索以及冗余计算操作,大大地降低了求解效率。文献[8]则提出了一种简单快速的完全可观测的不确定规划问题的强循环规划求解算法。文献[9]中探讨了在部分可观察下的规划问题,提出一种约减观察变量的方法。文献[10~12]提出了用分层法求最小权值规划解的方法,该方法是基于状态分层设计的一种方法,相对于文献[1]提出的反向搜索,通过实时更新所需搜索层数的上界和下界,从而避免了大量无用搜索和冗余计算,一定程度上提高了求解效率。
在实际生活中,由于受外部环境的干扰,不同状态之间转移和到达结果都是随机的、不确定的,而且不同状态在执行不同的动作时所要耗费的代价也是不同的。针对这一问题,本文对不确定规划问题中的动作赋权值,用概率来表示状态转移的不确定性。在求强规划解过程时,文献[13]提出了一种最小权值求强规划解的方法,该方法以耗费代价总和最小为目标函数,通过简单地累加规划解中动作权值来求得最小权值强规划解,意义不大。在分析现实生活中统计得到的数据时,用数学期望是为了准确地预期某件事未来可能的发展趋势。最小数学期望的研究首先开始于经济理论的研究,经济理论中的一个重要的研究课题是如何度量不确定环境下人们的偏好问题,与本文所提的不确定环境下的最优路径规划问题有类似之处。因此,本文尝试将最小期望权值引入来解决智能规划领域的问题。文献[14]提出了期望权值的概念,该文将其作为求解强循环规划解这一类问题的评判指标。该方法的主要思想是使用深度优先搜索求出规划问题的所有强循环规划解,再将解分别转换成以状态到目标状态的期望权值为变元的线性方程组,最后使用高斯消元法解方程组,从而找出最小期望权值强循环规划解。结合文献[13~14],本文提出求动作权值总和的期望值最小的强规划解,即最小期望权值强规划解。在执行强规划解时,因为每次从初始状态到达目标状态所执行过的动作个数是随机的,对应的所有动作的权值总和呈概率分布,此时动作的期望权值代表的是动作实际执行时所耗费的平均代价值。
本文首先将不确定规划问题中的目标状态集并入已搜索状态集,运用反向搜索求最小期望权值强规划解;在搜索过程中,需不断将最小期望权值所对应状态并入已搜索状态集,并更新未搜索状态集,迭代上述搜索步骤,直到已搜索状态集不变化为止,最后找出最小期望权值强规划解。
2 相关定义
定义1(规划领域)规划领域是一个不确定的状态转换系统,其中每个状态转换都有一定的概率分布;它可以表示成一个四元组,即∑=<S,A,γ,P>,其中:
S是一个有限状态集。
A是一个带权值的有限动作集。每个动作的执行是有耗费权值的,执行动作a用耗费权值cost[a](a∈A)表示。
γ.S×A→2S是一个状态转换函数。γ用来表示不确定性:γ=(s,a)表示状态s执行动作a所可能得到的结果状态集合;若γ=(s,a)非空,则称动作a在状态s下是可执行的。在状态s下可执行的动作集合记作 A(s)={a:∃s'∈γ(s,a)};其中,称 s'是s可达的,称(s,a)为状态动作序偶。
P是一个概率分布。对于动作a∈A以及状态s和s'∈S,Pa(s'|s)表示在状态s下执行动作a之后得到的结果状态是s'的概率。对于任意的s∈S ,若存在 a∈A 和 γ=(s,a)={s1',s2',…,sx'},那么就有
定义2(规划问题)规划问题是一个三元组Pro=<∑,S0,Sg>,其中 ∑ 是规划领域,S0⊆S是初始状态集合,Sg⊆S是目标状态集合。
定义3(执行结构)执行结构是一个二元组K=<Q,T>,其中,Q⊆S和T⊆S×S是满足以下条件的最小集合:
若s∈S,那么s∈Q。
若s∈Q且存在某个动作a使得(s,a)∈π,那么对所有的 s'(其中 s'∈γ(s,a))都有 s'∈Q 且(s,s')∈ T 。
状态s∈Q是K的一个终止状态当且仅当不存在状态s'∈Q,使得(s,s')∈T。 K是一个有向图,其中,Q是在执行规划解时能够到达的所有状态集合,T表示所有可能的状态转移。显然,K的终止状态代表规划执行的终止,这里用Sterminal(K)表示执行结构K的终止状态集。
定义4(强规划解)设 ∑=<S,A,γ,P>是一个规划领域,Pro=<∑,S0,Sg>是∑上的一个规划问题,π是规划领域∑中的一个状态动作序偶表,K=<Q,T>是π从S导出的执行结构。那么:
S是Pro的强规划解当且仅当K是无环的,且
若Pro有强规划解,则称可以从初始状态集强到达目标状态集;从初始状态集开始搜索强规划解,最终强到达目标状态集的过程称作强规划。
定义5(强规划的最小期望权值)设∑=<S,A,γ,P> 是 一 个 规 划 领 域 ,Pro=<∑,S0,Sg>是 ∑上的一个规划问题,则 Eπ是Pro的强规划的最小期望权值之和(简称最小期望权值)。当且仅当π、π'是Pro的强规划解,且对于 ∀π',都满足 Eπ≤Eπ'。 Eπ定义为
其中,cost[a](a ∈Act(si) )表示所需的代价,即执行动作a所耗费权值;E[sx]表示未搜索状态中新加入的状态所对应的期望权值之和,E[sl]表示sk所能到达的除sx的其他状态所对应的期望权值之和;由于状态之间的转换都是不确定的,所以Paj(sl|sk)表示由状态sk到达状态sl的概率。
3 算法思想及实现
由最小期望权值的定义(定义5)可知,执行最小期望权值强规划解的状态动作序偶集合πmin,不但可以保证系统能从初始状态到达目标状态,而且所需动作的期望权值最小。
3.1 算法思想
经济学中,数学期望是度量不确定环境下人们的偏好问题。那么本文所提的不确定环境下的最优路径规划问题也可类比应用数学期望来解决。由于是求解不同状态之间的最优路径,状态与状态转换之间的动作是不确定的、有概率的,我们将动作赋予权值,那么动作权值的最小期望即路径最小。
针对上述问题,本文设计了强规划的最小期望权值求解算法(LEC)。由于该算法首先将目标状态集Sg加入已搜索状态集Sgoal,然后反向搜索未加入中Sgoal的状态,从中找到能强到达Sgoal,且所需期望权值最小的状态;找到之后,将其加入Sgoal,并更新剩余未加入Sgoal中的状态到达已搜索状态集的最小期望动作权值;再迭代上述搜索步骤,直到Sgoal不再变化为止。
3.2 算法实现
设带权值的不确定规划问题P的状态集St中含有 n 个状态其中 Act(si)是从状态
si出发的动作集;E[si](1 ≤i≤n)用于保存从状态si出发到达目标状态的强规划解的最小期望权值,(即强规划解中的最小的期望权值之和);sAct[si](1 ≤i≤n)用于保存以状态si为初始状态的最小期望权值强规划解;sSet为已经求得的到达目标状态集且具有最小期望权值强规划解的状态集合;Sg表示目标状态集,Sgoal表示已搜索状态集目标状态集。
强规划的最小期望权值求解函数如下。
1)初始化;
2)更新到达已搜索状态集Sgoal所需的最小期望权值;
3)找强到达目标状态集且所需的期望权值最小的状态。
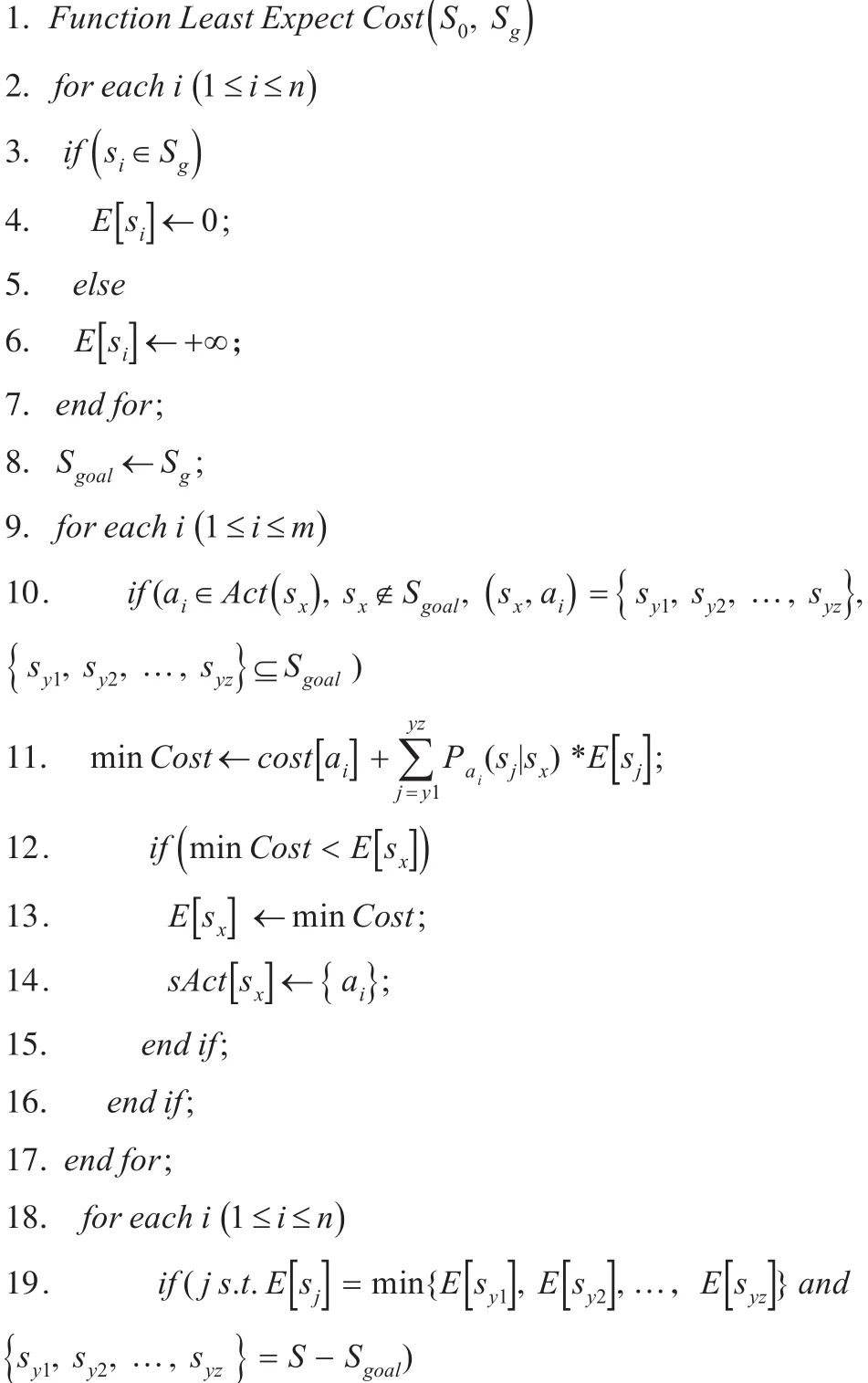

29. end if;
30. end if;
31. end for;
32.end for;
33.return E,sAct;
34.end;
第2~7行是初始化所有状态到达目标状态集的最小期望权值。其中,目标状态到达目标状态集的最小权值初始化为0;其余的状态到达目标状态集的最小权值初始化为+∞。
第8行是把目标状态集Sg加入到已搜索状态集Sgoal。
第9~17行是更新 S–Sgoal集合中的状态到达已搜索状态集Sgoal所需的最小期望权值。其中,第10行是对于动作ai,如果它是状态Sx下可执行的动作,且Sx尚未加入Sgoal,并且Sx执行动作ai所可能到达的状态集合,则执行第11行代码,计算状态Sx执行动作ai后,强到达目标状态集Sg所需的期望权值minCost。第12行是判断执行动作ai的方案是否优于已有的方案(即是否有,如果是,则在13、14行更新 E 和sAct;否则,保持原有方案。
第18~32行通过迭代来更新已搜索状态集Sgoal。每次迭代之后,都会从尚未加入Sgoal的状态中,将到达目标状态集所需期望权值最小的状态加入Sgoal;并更新其余尚未加入Sgoal到达目标状态集所需的最小期望权值。
第19~22行是从集合S–Sgoal中找到能强到达目标状态集且所需的期望权值最小的状态Sx,将其加入Sgoal。
第23~31行是在 Sx加入Sgoal之后,更新其余尚未加入Sgoal的状态强到达目标状态集所需的最小期望权值。其中第24行是判断尚未加入Sgoal的状态SK是否存在动作a能够通过Sx强到达Sgoal;如果是,则在第25行计算通过Sx强到达目标状态集的最小期望权值minCost;如果第26行判断minCost小于原来方案的值,则在第27-28行更新E[sk]和sAct[sk]。这里之所以强调是通过Sx强到达目标状态,是因为每次迭代都只在Sgoal中加入了Sx这个新元素;所以只需关注它所带来的改变就可以了;这样不但保证了算法本身的完备性,同时也减少了计算量。
3.3 算法时间复杂度分析
该算法分为三个步骤:1)初始化;2)更新到达已搜索状态集Sgoal所需的最小期望权值;3)找强到达目标状态集且所需的期望权值最小的状态。设有限状态集大小为n,带权值的有限动作集为m。
1)给定初始化部分算法复杂度为O(n)。
2)更新到达已搜索状态集Sgoal所需的最小期望权值。
若所有的 si执行动作 aj都到达 Sgoal,且mincost小于si的期望值,更新其mincost值,此时为次优解,其算法复杂度为O(m*n);若只有唯一一个Sgoal满足条件,即最优解,其算法复杂度为O(m)。
3)找强到达目标状态集且所需的期望权值最小的状态。
首先,需要计算状态集合中所有状态下的最小期望权值,并比较得出最小值;其次,迭代更新其余尚未加入Sgoal但却可以强到达目标状态集的状态,求出其所需的最小期望权值,此时如果尚未加入Sgoal的状态SK不存在动作a能够通过Sx强到达Sgoal条件,则算法取得最优解,其算法复杂度为O(n2);若满足该条件,同时计算出来的最小期望权值均小于当前状态的期望权值,则为次优解,次数复杂度为O(n3)。
4 算法实例分析
1)如图1所示,是一个带权值的不确定规划领域 ∑=<S,A,γ> 。 Pro=<∑,S0,Sg> 是 ∑ 上的一个规划问题。其中,S0={}s1是初始状态集合,是目标状态集合。规划问题Pro是在规划领域∑上求出从初始状态集合S0出发到达目标状态集合Sg的最小期望权值强规划解。
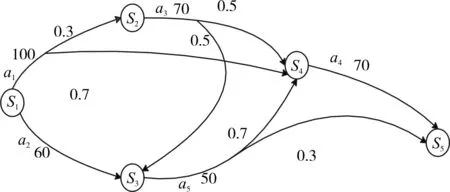
图1 带权值的不确定规划领域
算法首先对所有状态到达Sg的E[si]进行初始化。由上述可知,S1是初始状态,S5是目标状态,那么E[s5]=0+∞。

第二次搜索:将上一次搜索得到的状态S4并入Sgoal中,遍历其余状态,找到一个到目标状态的最小期望权值的状态。此时,Sgoal={s4,s5}。

第三次搜索:将上一次搜索得到的状态S3并入Sgoal中,遍历其余状态,找到一个到目标状态的最小期望权值的状态。因为 s1∉Sgoal,a1∈Act(s1γ(s,所以根据minCost公式,可得到E[s1]=159,sAct[s1]={a2, a5, a4} 。
然后再循环,执行第四次、第五次搜索等,直到已搜索状态集合S0中的所有状态不再变化为止。
通过上述搜索,最终得到从由S1到S5的强规划期望权值解为期望权值为159。
2)如图2所示,通过增加不确定规划问题的状态数与动作数,重新按照上述步骤进行求解,我们同样可以获得最小期望权值强规划解。
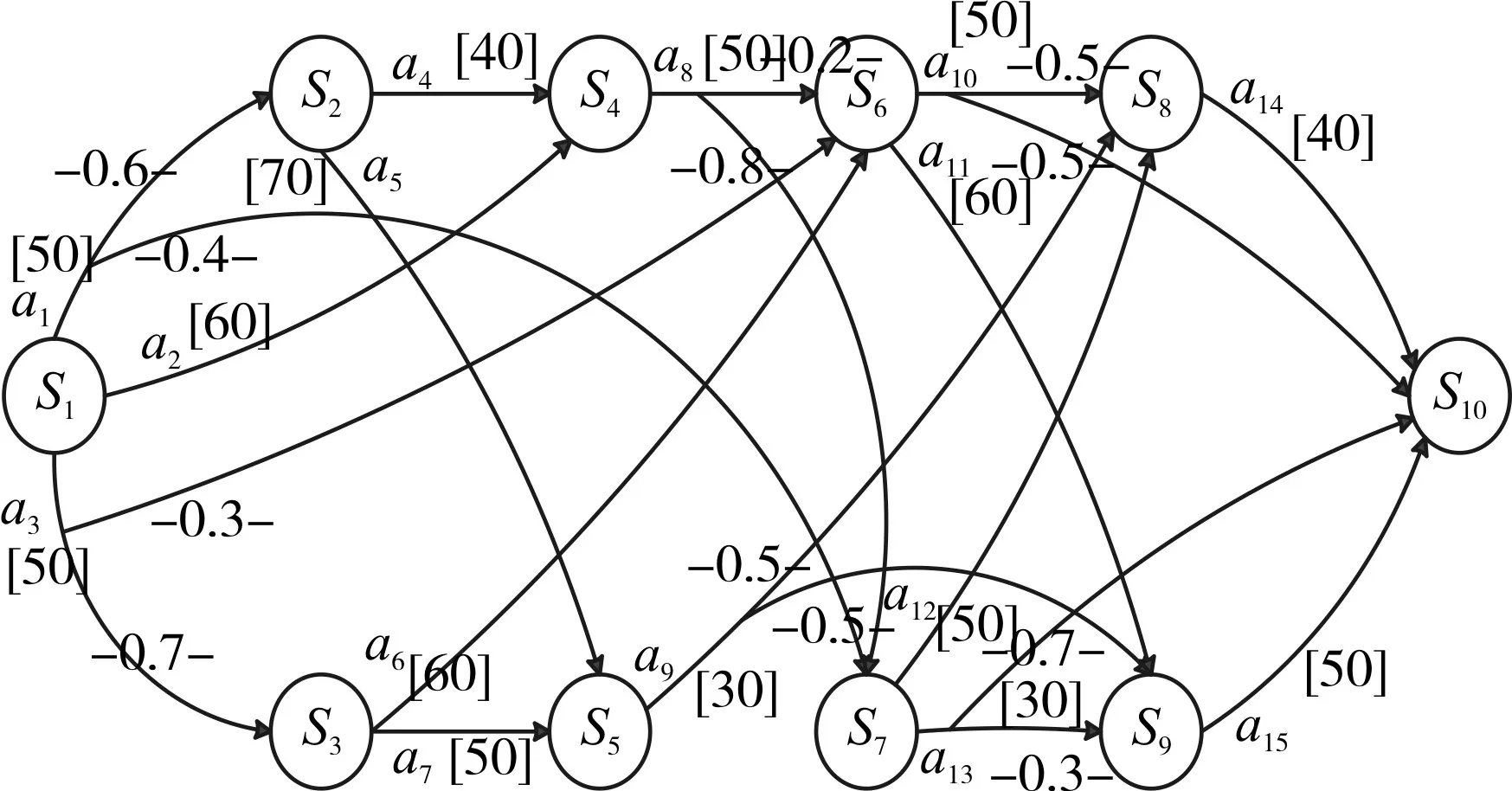
图2 增加状态数与动作数后的带权值不确定规划
S1是初始状态,S10是目标状态,那么E[s10]=0,均为+∞。

第二次搜索:将上一次搜索得到的状态S8并入Sgoal中,遍历其余状态,找到一个到目标状态的最小期望权值的状态。此时,Sgoal={s8,s10}。

然后再循环,执行第四次、第五次搜索等等,直到已搜索状态集合S0中的所有状态不再变化为止。
通过上述搜索,最终得到从由S1到S10的强规划 期 望 权 值 解 为 :最小期望权值为162。
5 算法实验分析
本文的实验环境为:Windows10+Intel®CoreTMi5-4590@3.3GHz+4GB内存。
根据本文提出的LEC算法设计实验,可以较快地求出不确定规划问题的强规划解,且所需要的期望权值之和近似最小。文献[13]最早提出最小权值强规划解的概念,本文所设计的LEC算法与其进行运行时间的比较,文献[13]的算法在试验中用“算法1”表示,本文算法用“算法2”表示。通过几组不同的状态数的不确定规划下进行50组实验数据的平均运行时间比较,如表1所示。
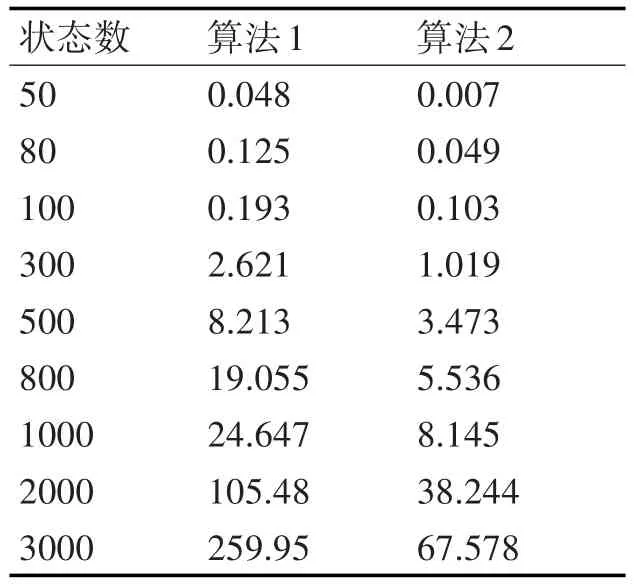
表1 求解最小权值强规划解的运行时间比较
上述实验是在状态数与动作数相等的条件下进行比较,为了更进一步评判本文所提出的LEC算法,在状态数相同的情况下,通过增加动作数进行实验比较时间代价,通过几组不同的状态数以及不同的动作数进行50组实验数据的平均运行时间比较,如表2所示。
表1的试验中“算法1”和“算法2”分别用了分层策略和LEC权值两种不同的策略进行算法设计,从实验结果分析来看,在动作数和状态数相同的情况下,“算法2”的实验时间代价明显低于“算法1”。
现实生活中,不确定的动作数往往是大于其状态数的,表2的实验中,通过状态数相同,增加动作数的实验来比较其时间代价。实验预期结果是:当状态数一样,大量增加不确定动作数时,计算最小期望权值的时间会较繁琐,其时间代价会迅速增加。但是,表2的实验结果却显示其时间代价增长较缓。通过进一步的分析研究,大量增加动作数后,算法只会选择符合已加入Sgoal的最小期望权值,其余不满足条件的,算法直接将其过滤,从而节省了一部分时间。
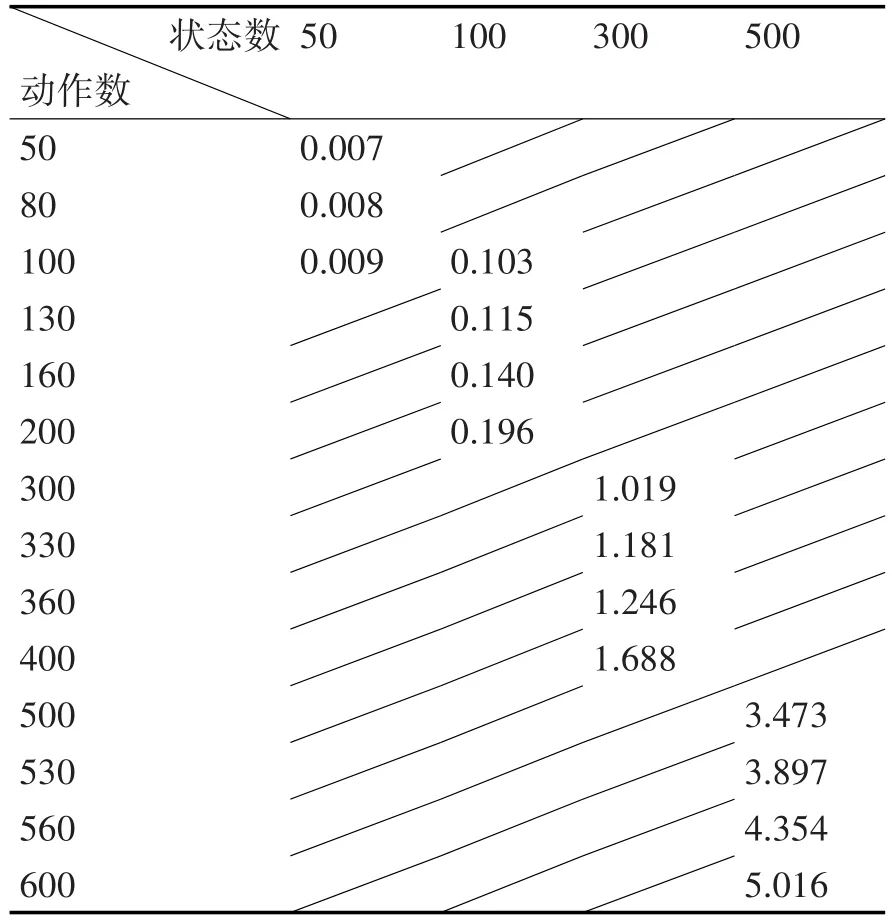
表2 状态数相同动作数不同的运行时间比较
通过与文献[13]在状态数与动作数相等的情况以及状态数相同、动作数增加的两组对比试验,我们可以得到以下结论:1)通过LEC算法求解最小权值强规划解减少了时间代价;2)LEC算法加入不确定因素,更满足实际情况,加入后随着动作数的增加,时间代价增加较缓,这是因为不确定规划下不确定的动作增加使得要求的最小期望权值更明确,从而能在众多的动作下选择最小期望权值的强规划解。
6 结语
针对不确定规划问题,本文设计了LEC算法。该算法通过将不确定规划问题中的目标状态集并入已搜索状态集,然后通过反向搜索各状态到达目标状态的最小期望权值强规划解,直到求出初始所有的状态的最小期望权值强规划解,停止搜索。实验结果表明,使用本文设计求强规划解算法,可以求出最小期望权值强规划解,从而验证了算法的正确性,同时在符合实际条件下,该算法规避了许多不确定的动作数,算法效率更高。今后可以从以下方面进行研究:
1)将求解最小期望权值强规划解的思想应用到多Agent规划领域;2)改进本文所设计的算法,用于求解最小期望权值弱规划解;3)将状态分层与本文所设计方法相结合,进一步提升强规划解求解的速度与精度。
[1] Ghallab M,Nau D,Traverso P.Automated Planning The-ory and Practice[M].[S.l.]:Massachusetts:Morgan Kaufmann Publishers,2004:1101-1132.
[2]丁德路,姜云飞.智能规划及其应用的研究[J].计算机科学,2002,29(2):100-103.DING Delu,JIANG Yunfei.Intelligent Planning and its Application[J].Journal of computer sci-ence,2002,29(2):100-103.
[3]Kuter U,Nau D,Reisner,et al.Using Classical Planners to Solve Nondeterministic Planning Problems[C]//Proc.of the 18th IntConf on Automated Planning and Sched-uling.Menlo Park,CA:AAAI press,2008:190-197.
[4]M.Ghallab,D.Nau,P.Traverso.Automated Planning:Therory and Practice[M].Handbook of Knowledge Representation,2004.
[5]饶东宁,蒋志华,姜云飞,等.对不确定规划中观察约见的进一步研究[J].软件学报,2009,20(5):1254-1268.RAO Dongning,JIANG Zhihua,JIANG Yunfei,et al.Further Research on Observation Reduction in Non-Deterministic Planning[J].Journal of software,2009,20(5):1254-1268.
[6]Cimatti A,Roveri M,Traverso P.Strong planning in nondeterministic domains via model check-ing[C]//Proceedings of the 4th International Conference on Artificial Intelligence Planning Sys-tems(AIPS’98).USA:Carnegie Mellon Univer-sity,1998:36-43.
[7]CIMATTI A,PISTORE M,ROVVERI M,et al.Weak,strong,and strong cyclic planning via symbolic model checking[J].Artificial Intelligence,2003,147(1-2):35-84.
[8]Fu J,Bastani F B,et al.Simple and fast strong cyclic planning for fully-observable nondeterministic planning problems[C]//IJCAI Proceedings-International Joint Conference on Artificial Intelligence.2011:1949-1954.
[9]周俊萍,殷明浩,谷文祥,等.部分可观察强规划中约减观察变量的研究[J].软件学报,2009,20(2):290-304.ZHOU Junping,YIN Minghao,GU Wenxiang,et al.Research on Decreasing Observation Varaiable for Strong Planning underPartialObservation [J].Journalof soft-ware,2009,20(2):290-304.
[10]Bertoli P,Cimatti A,Roveri M,et al.Strong planning un-der partial observability[J].Artificial Intelligence,2006,170(4/5):337-384.
[11]陈建林,文中华,朱江,等.正向搜索方法求强规划解[J].计算机工程与应用,2011,47(6):52-54.CHEN Jianlin,WEN Zhonghua,ZHU Jiang,et al.Strong planning solution via forward search[J].Computer Engi-neeringand Applications,2011,47(6):52-54.
[12]伍小辉,文中华,李洋,等.分层法求最小权值强规划解[J].计算机科学,2015,42(2):228-232.WU Xiaohui,WEN Zhonghua,LI Yang,et al.Solving Minimal Cost Strong Planning Solution by Hierarchical Algorithm[J].Computer Science,2015,42(2):228-232.
[13]陈建林,文中华,马丽丽,等.一种求解最小权值强规划的方法[J].计算机工程,2011,37(17):167-171.CHEN Jianlin,WEN Zhonghua,MA Lili,et al.Method of Solution Minimal Cost Strong Planning[J].Computer Engineering,2011,37(17):167-171.
[14]李洋,文中华,伍小辉,等.求最小期望权值强循环规划解[J].计算机科学,2015,04:217-220,257.LI Yang,WEN Zhonghua,WU Xiaohui,et al.Solving Strong Cyclic Planning with Minimal Expectation Weight[J].Journal of computer science,2015,04:217-220,257.

