追踪与目标航天器相对位姿参数四元数的解析算法
冯 春 吴洪涛 陈 柏 乔 兵
南京航空航天大学,南京,210016
0 引言
利用计算机视觉进行空间目标物位姿估计是当前光学测量和航天工程等领域的研究热点之一。基于视觉的相对位姿确定方法在机器人视觉伺服、卫星编队和航天器交会对接等方面有着广泛的应用[1-2]。在航天器空间交会的最后阶段,通常采用CCD相机进行追踪和估计航天器与目标航天器间的相对位姿,国内外学者已经就相关问题开展了大量的研究工作[3-13],其中传统的方法就是利用单目视觉进行测量,该方法简单、可靠且方便,是双目和多目视觉测量方法的基础。
Mukundan等[7]提出采用3个非共线特征点,利用四元数理论得到一个一元四次方程,求解方程获得追踪航天器与目标航天器间的相对位置和姿态的解析解,但求解四次方程时会出现多值问题,需要加以区分和判别,带来了识别方面的困难,且在特定形式下会出现奇异值。李建锋等[8]采用5个非共面特征光点,选取其中3个对称特征光点为一组,共两组,每一组利用数值迭代的方法求解相应的参数并将两组结果取平均值作为最后计算值,该方法是原始问题研究中的一个进步,解决了多解判断的问题,但迭代方法存在实时性、准确性及收敛性等困难。
本文采用5个非共面特征光点构成两组均为3个“T”形配置的目标航天器非共线特征光点,基于单目视觉获取四元数分量和2个航天器之间距离的5个方程。然后对这些方程进行变量替换,求出相对位置和姿态参数的解析解,同时对所求得的解析解进行修正,从而有效解决了文献[7]中的多值问题和奇异值问题,避免了文献[8]中采用迭代方法计算时的初值选取、迭代实时性和收敛困难等问题,是对文献[7]和文献[8]的一种改进。最后利用数学仿真验证了本文算法的有效性,是当前这类问题一种理想的解决方案。
1 位姿测量系统结构
利用光学相机进行最后阶段航天器交会对接相对位姿测量的系统结构如图1所示。特征目标是在目标航天器上以固定几何关系分布的特征点光源。相对位姿参数测量系统主要包括:相机标定、图像采集、图像畸变校正及滤波、特征点提取、相对位姿解算等步骤。

图1 位姿参数测量系统结构图
对于特征光点的结构,本文采用5个非共面特征光点构成特定几何关系配置的形式,这是考虑到利用3个非共线的特征点(其确定的平面不与相机的光轴正交)就可以唯一确定相对姿态参数,但为了保证任何时刻光学相机视场范围内至少有3个非共线的特征光点,故特征光点的设计采用了图2所示的结构和坐标,该结构既便于测量,又能使目标特征光点具有一定的冗余性[7-8]。

图2 特征光点设置及航天器和相机坐标系
2 单目视觉相对位姿确定算法
为了分析问题方便,建立了图2中的三种坐标系,即目标航天器坐标系o(x,y,z)、摄像机坐标系O(X,Y,Z)和像平面坐标系Oi(U,V)。三坐标系具有的特点如下:
(1)目标航天器坐标系o(x,y,z)定义在目标航天器的特征点上,采用3个特征光点构成“T”形,坐标轴可依据所需特征光点的几何关系设定。
(2)摄像机坐标系O(X,Y,Z)将原点O作为摄像机的光心,X、Z轴分别与图像坐标系的U、V轴平行,Y轴为摄像机的光轴,与图像平面垂直。
(3)图像坐标系Oi(U,V)是以像素为单位的坐标系,U、V是每一像素在图像中的列值和行值,它的原点Oi是摄像机光轴与图像平面的交点,它与摄像机坐标系原点O之间的距离即为摄像机的焦距f。
2.1 单目视觉四元数位姿测量方法
假定相机已经精确标定,并且特征光点位置坐标与图像坐标均正确匹配,则在相机坐标系中的像平面可以表示为Y=-f。为完整起见,本文仿照文献[8]并加以推广,将特征光点s i(x i,y i,zi)在相机坐标系中的对应点坐标标记为S i(X i,Y i,Zi),从而由刚体的旋转和平移变换可得

式中,R为旋转矩阵;t为平移矩阵。
用四元数表示的旋转矩阵为
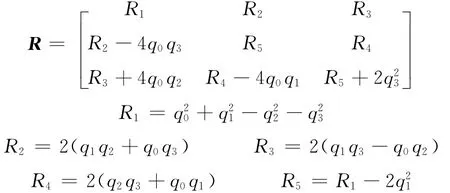
单位四元数的4个参数qi(i=0,1,2,3)的约束方程为

在图2中取“T”形结构的3个特征光标点s1、s2、s3,它们在目标坐标系中的坐标可表示为

目标航天器上的特征光点在相机坐标系中的坐标S i(Xi,Y i,Zi)(i= 1,2,3)与 图 像 坐 标 系(U i,V i)(i=1,2,3)之间的关系可利用透视投影变换方程表示为
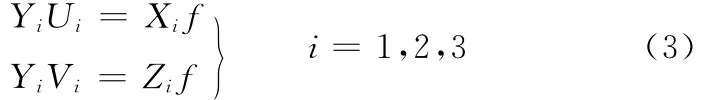
实际应用中两航天器之间的距离ty远远大于特征光点之间的深度差(即a,b≪t y,则有Y i≈t y),故上述方程变换为

将特征光点s i(x i,y i,zi)代入式(1),则其在相机坐标系中的坐标值为

将式(4)代入式(5)、式(6)、式(7),可得四元数的4个分量与ty的关系表达式:

同理,“T”形结构的3个特征光标点s4、s2、s5在目标坐标系中的坐标可表示为

四元数的4个分量与t y的关系式为
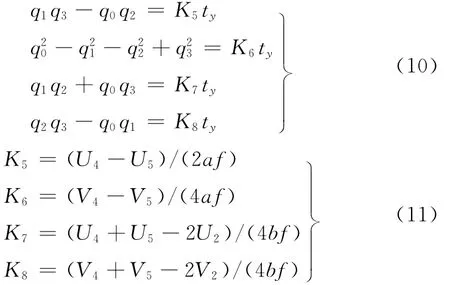
联立式(8)和式(10)有等式

考虑到t y一般为正,因此取正平方根,而且Ki(i=1,2,…,8)不会同时为零,故有
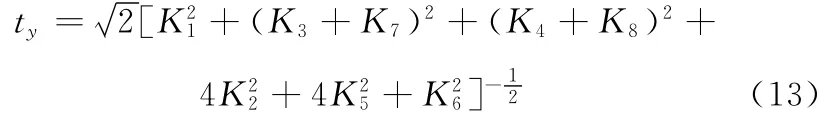
另外2个参数tx、tz和另外4个未知量的求解表达式为
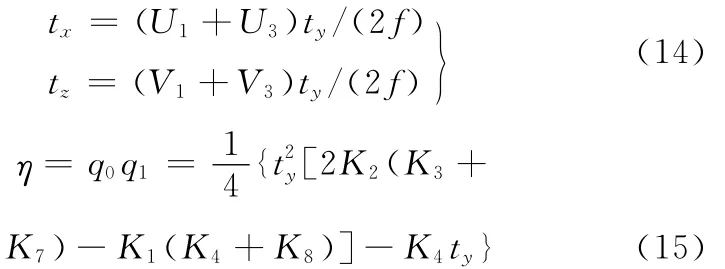
由式(8)和式(2)可得

由式(15)、式(16)可得
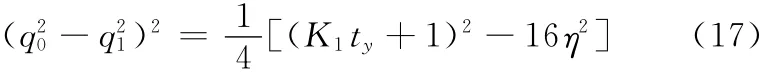
考虑到2个航天器之间的旋转角度不应该太大,而当旋转角满足|φ|<90°时有q0>q1,故此时式(17)选择正的平方根,即
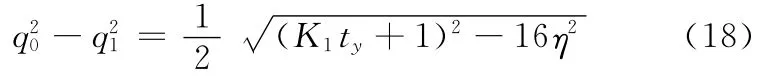
通过式(15)、式(16)和式(18)可得
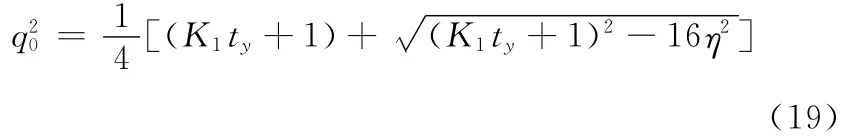
由于数学上q0取正号或者负号的时候,获取的相应四元数表示绕同一旋转轴的相同旋转,经验值一般选取q0>0,故有表达式:
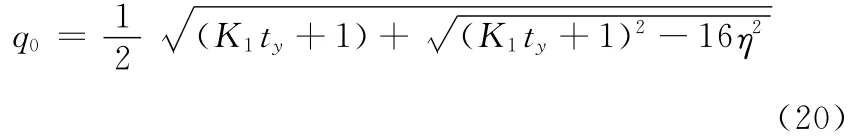
由η=q0q1可得

得到q0、q1后,若式(17)右端不为0,则可利用式(8)和式(10)求得q2、q3,其表达式为
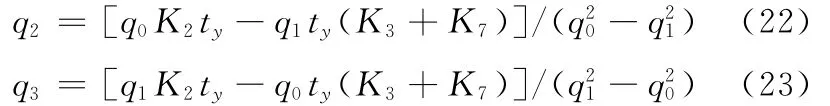
2.2 正交比例投影误差修正
在两航天器之间距离ty远大于特征点景深(Y i-Y j)(i≠j)条件下,正交比例投影可以作为透视投影的近似,即利用式(4)代替式(3)进行近似计算。图2选定的5个特征光点中的s1、s3、s4、s5处于同像平面平行的平面内,而s2在距离该平面b处,故式(4)的结果会存在误差,需要进行修正,其表达式为

相应地,式(8)的第三分式和第四分式与式(10)的第三分式和第四分式变为

则式(15)修正为
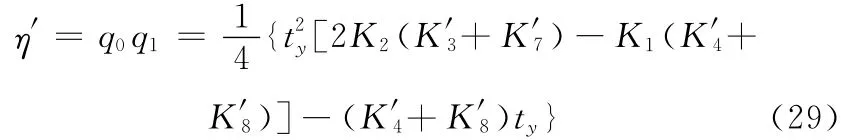
将修正的η′代入式(20)和式(21)计算得到修正后的q0、q1,四元数的另外2个分量的修正表达式为

在完成了上述四元数各分量的求取后,根据欧拉角与姿态矩阵元素的对应关系,可以得到四元数的4个分量与航天器相对姿态角θ(俯仰)、ψ(偏航)、φ(滚动)的关系表达式:
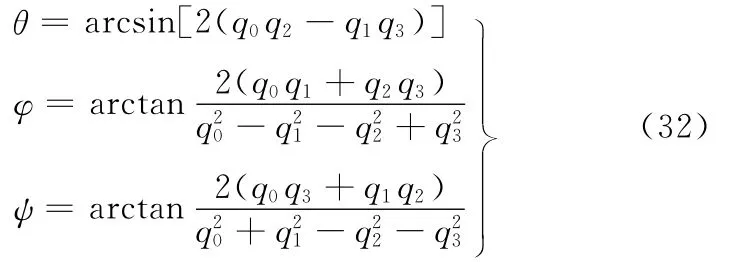
上述分析表明:文献[7]的本质是将一元四次方程的四元数特征和两组特征点化为一组递进的一元二次方程组,并经优化选择,从而获得(ty,q0,q1,q2,q3)5个变量的唯一解。本文将几何、数学和光学测量方法相结合,采用显式方式求取5个变量的唯一解,避免了数值方法的初值选取与收敛性判断等繁复不便。
进一步,当两航天器距离越来越接近,即正交比例投影的近似条件不再满足时,相关Ki系数需要修正,此时解析方程组形式不变,仍可用上述方程求解。
3 数值仿真
为了验证本文算法获取的航天器位姿参数解析解的有效性,选用MATLAB软件对该算法进行数学仿真。仿真的相关条件参照文献[7]进行设置。仿真结果如图3、图4、图5所示。
目标航天器上的特征光点为s i(x i,y i,zi)(i=1,2,…,5),目标坐标系中的坐标值表达式为

图3 修正前的相对位姿参数估计误差

图4 修正后的相对位姿参数估计误差

相机的焦距f=0.1m。假定两航天器姿态一致,即四元数q=[1 0 0 0],3个坐标轴的相对平移量为t x∶t y∶tz=5.2∶20∶2,目标航天器与相机距离从20m变化到1m(在交会对接的最后阶段,两航天器相对姿态比较小,可以作上述假设)。图3为未修正之前的位姿参数误差仿真结果。

图5 位置不变时的相对位姿参数误差
图4为修正后的相对位姿参数估计误差,从图中可以看出,通过对解析解的修正,相对姿态的参数估计精度有了较大的改善,修正后的相对姿态角估计误差在5m以外时小于0.7°。随着相对距离的减小,相对姿态参数估计误差逐渐增大,在小于5m时,误差急剧增大。原因是比例正交投影近似的条件是两航天器之间的距离ty需远大于特征点的景深(Yi-Y j)(i≠j)。
下面分析两航天器相对姿态大小对其相对位姿测量参数误差的影响,假定两航天器之间相对位置关系不变,即t=[5.2 20 2],固定3个姿态参数的其中2个,增大另一个,使单轴姿态角变化20°。由图5仿真结果可知,相对位置最大估计误差为0.022m,相对姿态最大估计误差为0.63°。由于修正项是基于标称相对位置和姿态得出的,所以当相对姿态偏差较小时,本文的算法完全可以满足测量精度的要求。
4 结语
本文提出的解析算法简化了相对位姿参数确定问题的计算过程,计算量小,计算速度快,可以满足航天器交会对接单目视觉测量的实时性要求。通过数学仿真,验证了本文提出的交会对接最后阶段相对位姿参数估计算法的可行性和有效性。
[1]John L J,Declan C H,Karim P W,et al.Visionbased Navigation for Rendezvous,Docking and Proximity Operations[R].Cranfield:American Astronomioal Society,1999.
[2]Beard R W,Lawton J,Hadaegh F Y.A Coordination Architecture for Formation Control[J].IEEE Transactions on Control System Technology,2001,9(6):777-790.
[3]Philip N K,Ananthasayanam M R.Relative Position and Attitude Estimation and Control Schemes for the Final Phase of an Autonomous Docing Mission of Spacecraft[J].Acta Astronautica,2003,52:511-522.
[4]林来兴,李灿.交会对接最后逼近阶段CCD相机的测量方法[J].宇航学报,1994,15(2):24-34.
Lin Laixing,Li Can.CCD Camera-based Measurement for the Final Phase of RVD Mission[J].Journal of Astronautics,1994,15(2):24-34.
[5]杜小平,赵继广,崔占忠,等.基于计算机视觉的航天器间相对状态测量系统[J].光学技术,2003,29(6):664-666.
Du Xiaoping,Zhao Jiguang,Cui Zhanzhong,et al.Optical Method for Position-attitude Determination between Spacecrafts Based on Computer Vision[J].Optical Technique,2003,29(6):664-666.
[6]张庆君,胡修林,叶斌,等.基于双目视觉测量的航天器相对位置和姿态的测量方法[J].宇航学报,2008,29(1):156-161.
Zhang Qingjun,Hu Xiulin,Ye Bin,et al.Binocular Vision Based Relative Position and Attitude Determination between Spacecrafts[J].Journal of Astronautics,2008,29(1):156-161.
[7]Mukundan R,Ramakrishnan K R.A Quaternion Solution to the Pose Determination Problem for Rendezvous and Docking Simulations[J].Mathematics and Computers in Simulation,1995,39:143-153.
[8]李建锋,杜小平,张彗星.基于四元数的航天器间相对姿态光学测量方法研究[J].航天控制,2011,29(2):46-51.
Li Jianfeng,Du Xiaoping,Zhang Huixing.The Research on Spacecraft Relative State Optical Measurement Based on Quaternion[J].Aerospace Control,2011,29(2):46-51.
[9]徐文福,梁斌,李成,等.基于立体视觉的航天器相对位姿测量方法与仿真研究[J].宇航学报,2009,30(4):1421-1428.
Xu Wenfu,Liang Bin,Li Cheng,et al.The Approach and Simulation Study of the Relative Pose Measurement between Space-crafts Based on Stereo Vision[J].Journal of Astronautics,2009,30(4):1421-1428.
[10]王保丰,李广云,陈继华,等.航天器交会对接中测量靶标的两种设计方法[J].宇航学报,2008,29(1):162-166.
Wang Baofeng,Li Guangyun,Chen Jihua,et al.Two Methods of Coded Targets Used in Rendezvous and Docking[J].Journal of Astronautics,2008,29(1):162-166.
[11]Wilson J R.Satellite Hopes Ride on Orbital Express[J].Aerospace America,2007,45(2):30-35.
[12]Tafazoli M.A Study of on-orbit Spacecraft Failures[J].Acta Astronautica,2009,64(2/3):195-205.
[13]徐文福,梁斌,李成,等.空间机器人捕获非合作目标的测量与规划方法[J].机器人,2010,32(1):61-69.
Xu Wenfu,Liang Bin,Li Cheng,et al.Measurement and Planning Approach of Space Robot for Capturing Non-cooperative Target[J].Robot,2010,32(1):61-69.
(编辑 何成根)

