无人机动平台着陆惯性/视觉位姿歧义校正算法
尚克军,郑 辛,王旒军,扈光锋,刘崇亮
(1.北京理工大学 自动化学院,北京 100086;2.北京自动化控制设备研究所,北京 100074)
长航时无人机由于其留空时间长,多采用太阳能结合储能电池系统作为动力能源,因而要求结构质量尽量轻,结构设计上多采用取消起落架配置,能够满足长航时无人机减小起飞重量、简化结构设计的需求[1]。在移动平台上设置合作目标并敷设回收网,通过对无人机速度和位置的精确控制,使无人机平稳降落至柔性的回收网中,实现无人机的回收,是有效可行的回收方式之一。
以视觉二维码作为合作目标,使用单目相机只进行一次观测即可解算出相机与二维码之间的相对位置和姿态(即为典型的PnP(Perspective-n-Point)问题),具有很强的便利性和灵活性。视觉二维码已成为机器人、无人车与无人机领域常用的位姿估计手段。
针对PnP 问题有许多经典的解法,诸如使用三对点的P3P、直接线性变换(Direct linear transformation,DLT)、EPnP 和UPnP 等。由于单个二维码是平面目标,四个三维角点满足共面约束,二维码平面与图像平面之间变换为单应矩阵(Homography),进而使用二维码进行位姿解算是平面位姿估计(Plane-based Pose Estimation,PPE)问题。
PPE 问题的求解包含两类主要方法:其主流解法是首先估计二维码平面与图像平面之间变换为单应矩阵,然后使用单应阵分解(Homography Decomposition,HD)求得相对位姿的解析解;另一类常用求解方法将PPE 视为PnP 问题的特例直接使用PnP 求解方法计算相对位置和姿态。
理论上,使用任意三点不共线的四个共面点(如方形二维码四个角点)进行6 自由度位姿解算具有唯一解。实际上,尽管PPE 问题有许多成熟的求解方法,但是基于二维码的位姿解算深受位姿歧义的困扰,约25%情况位姿解算结果具有歧义性[2]。
目前解决PPE 问题位姿歧义有以下几类常用方法:
1)添加额外二维码组成二维码序列[3]。一种方案是添加多个共面二维码组成组合二维码:如果各二维码之间位置关系已知,则直接使用4n(n为检测到的二维码个数)个3D-2D 对应点对计算相对位姿。如果各二维码之间位置关系未知,则需要先求出每个二维码的位姿结果,然后再利用所有二维码的位姿一致性选取正确的结果;另一种方案是添加多个非共面二维码:如果一副图像中识别出多个二维码,则多个3D-2D点对打破了共面条件的约束,该PnP 问题具有唯一解。
需要注意的是,不论添加额外的共面还是非共面二维码,能解决位姿歧义问题的前提是组合二维码在图像中成像面积足够大,否则就会陷入单个二维码位姿歧义的场景,多个二维码与单个二维码的作用效果没有差别。
2)基于时间序列滤波的方法[4,5]。使用卡尔曼滤波器、扩展卡尔曼滤波器或粒子滤波器等方法建模相机运动模型,对当前位姿结果进行预测,选取符合模型的结果。
基于滤波的方法假设二维码位姿的变化具有时间连续性,而位姿歧义会导致位姿解算结果随机震荡,导致不能建立准确的运动模型,使得滤波器能减少正确位姿之间错误的位姿估计,但是如果初始位姿估计错误,则滤波平滑后的相机运动轨迹可能一直为错误估计。
无人机动平台着网回收场景下二维码合作目标与机载相机都在运动,其相对位姿关系没有确定的模型,并且着网回收过程起始于无人机与二维码目标距离较远的地方,位姿歧义可能频繁出现,基于滤波方法结果的不确定性会导致灾难性的后果。
3)利用深度信息矫正位姿歧义[6]。使用双目或RGBD 相机可以获取二维码目标的深度信息,融合二维码的深度信息可提升位姿估计精度并解决位姿歧义问题。
但是目前RGBD 相机有效作用距离为5 m 左右,且在室外日光条件下深度传感器无效。无人机动平台着网回收场景起始于无人机与二维码目标距离较远的地方,远超出双目或RGBD 相机有效作用距离,不能消除位姿歧义。
本文针对无人机移动平台着网回收应用场景,通过构建非共面二维码合作目标,并融合IMU 传感器信息,提出了一套基于二维码的惯性/视觉位姿歧义校正算法,重点解决无人机回收过程中位姿解算歧义问题,提升无人机动平台回收的导航精度、鲁棒性与实用性。
1 二维码合作目标设计
目前常用的二维码大致可分为方形二维码、圆形二维码和异形二维码等。方形二维码具有正方形的外边界,一般由黑色边框包围,内部含有二进制或特定视觉模式等编码信息,利用方形二维码外边界的四个角点可进行位姿解算。常见的方形二维码有ARToolKit、AprilTags[7]和ArUco[8]等;圆形二维码使用圆轮廓作为识别特征,编码信息包含于圆形扇面或者同心圆环中。圆形二维码通常只有圆心点特征,单个圆形码不能进行位姿解算。常见的圆形二维码有Intersense 和CCTag[9]等;除方形和圆形二维码外,还有一些不规则形状的二维码,如STag[10]和TopoTag[11]等。
方形码由于其具备简单的编码方式,并且单个码即可提供四个角点用于位姿估计,在增强现实和机器人技术等领域应用广泛,在各型二维码中占主导地位。本文基于方形码设计了一套组合二维码。
该组合码包含三个方形二维码,二维码内部使用简单的二进制编码,并且以不同的打印尺寸组合成立体码,其主要设计理念如下:
1) 为了适应无人机着网回收远距离(≥20m)识别定位的需求,二维码内部使用简单的9位二进制编码,易于远距离分辨识别;
2) 无人机着网回收过程末段二维码与机载相机的距离较近,可能会使单个二维码成像不完整,导致识别与位姿解算失败。本文使用不同尺寸的二维码以一定的空间关系排布形成组合二维码(见图1(a)),只要识别大于或等于一个任意二维码就能确定相机与组合码的相对位姿关系。较大尺寸的2#码主要用于远距离识别定位,而0#和1#码设计较小的尺寸主要用于近处的识别定位,组合二维码详细尺寸见图1。该组合二维码同时具备作用距离远和近处防遮挡的特性;
3) 使用单幅图像中共面的特征点进行位姿估计会得到四个不同的解,根据“Cheirability”约束可以剔除其中的两个错误解,最终获得两个可能的解。大多数视角下可以使用最小化重投影误差判别两个解中正确的一个,然而当相机与二维码距离较远时,利用重投影误差等手段不足以判别两个解的正确性,从而导致姿态的歧义[13]。本文通过将0#和1#码上抬45 °构建非共面组合二维码,并结合IMU 传感器,用于优化相对位姿解算并解决位姿歧义问题(详细分析见第2 节)。
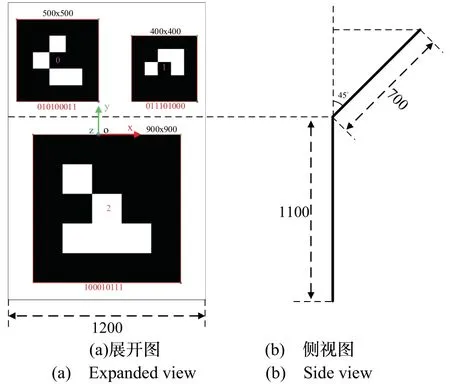
图1 组合二维码设计示意图Fig.1 Schematic diagram of marker map design
2 位姿歧义校正算法
2.1 位姿歧义问题
以平面二维码为合作目标进行位姿解算时,多数情况下通过比较返回位姿结果的重投影误差并使用最小重投影误差可以判别正确的位姿解,但是当二维码合作目标尺寸较小或相机与二维码的距离远远大于相机的焦距时,二维码角点检测结果不可避免地携带较大的噪声干扰。这时,二维码在成像平面投影透视效应很弱(Weak-Perspective),二维码平面与图像平面之间单应矩阵近似为仿射变换(Affine Transformation),仅利用重投影误差手段不足以判别两个可能解的正确性,从而导致位姿解算的歧义。
如图2所示,红色圆区域表示二维码角点可能的检测误差范围,左右两种颜色的立方体表示两个可能的位姿结果T和T′(T与T′是以相机光心和二维码中心连线为法线的平面的一对翻转)。由于角点成像噪声影响,无法区分这两种位姿投影产生的成像结果,位姿解算结果会在T和T′这两种结果之间随机震荡,使得位姿解算具有歧义性。此种情况下,尽管2D 像素位置几乎没有差别,但解算得出的两3D 位姿差别较大。因此,通过随机选取一个解或者计算两个解的中间值都不是可行的方案。
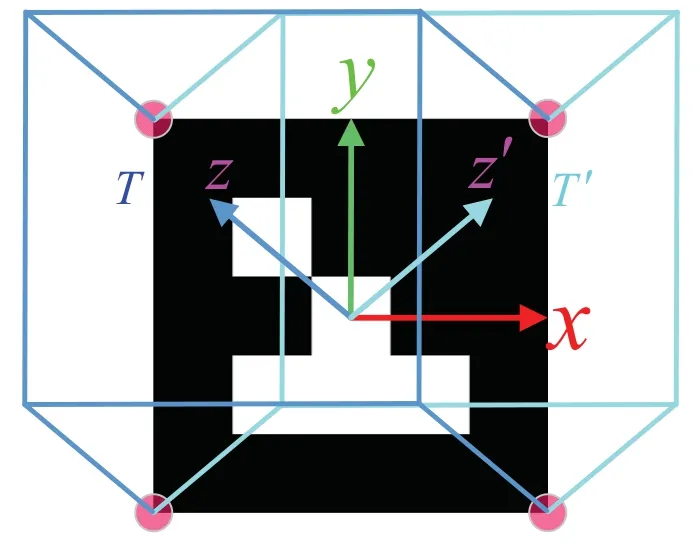
图2 位姿歧义示意图Fig.2 Pose ambiguity
2.2 位姿解算与歧义校正
针对无人机动平台着网回收应用场景,本文通过添加额外的二维码构建组合二维码,并将0#和1#码上抬45 °构建非共面二维码序列,使用非共面3D-2D 点对打破共面约束,用于优化较近距离(≤10m)位姿解算。此外,通过融合IMU 传感器引入姿态约束,解决无人机着网回收过程中的相对位姿解算歧义问题。
使用文献[3]方法进行二维码的检测识别,获取各二维码角点坐标以进行后续的位姿解算。位姿解算与歧义校正流程如图3所示,主要包含二维码角点坐标优化、极小化平面位姿估计算法(IPPE)、位姿歧义校正和位姿优化等步骤。
2.2.1 角点坐标优化
精确的角点坐标有利于提升位姿解算的精度,并能一定程度抑制位姿歧义的发生。二维码识别步骤获取了各二维码粗略的角点坐标,携带较大的噪声干扰,需要进行角点亚像素坐标优化。
考虑到二维码四个角点为其四条边线交点的事实,单纯通过设定近邻窗口进行角点的亚像素优化可能不满足二维码设计时的几何约束。本文使用二维码每个边上的轮廓点进行最小二乘拟合获取四条边的直线方程,然后通过两两直线求交点计算四个角点的亚像素坐标。角点坐标优化效果如图3中所示,红色角点为二维码识别步骤获得的粗略坐标,绿色点为亚像素优化后的角点坐标,可以看出经过坐标优化,角点坐标更加准确,可以提升位姿解算精度,并在一定程度上避免位姿歧义的产生。
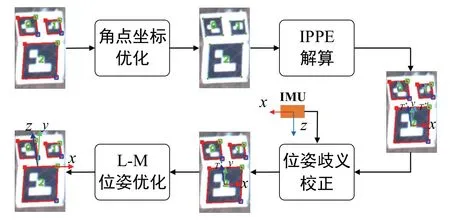
图3 位姿解算与歧义校正处理流程Fig.3 Pose estimation and ambiguity correction
2.2.2 IPPE 位姿解算
IPPE(Infinitesimal Plane-based Pose Estimation)算法[14]是一种利用n(n≥ 4)个3D-2D 对应点对计算平面目标三维位姿的快速求解方法。IPPE 针对PPE问题进行优化,对PPE 问题进行解析求解,其求解速度比通用PnP 求解方法要快得多,并且大多数情况下精度也更高。此外,IPPE 算法在处理位姿歧义情况时具有显著的优势:IPPE 算法总是返回两个候选位姿解算结果及其各自的重投影误差,并且位姿结果使用重投影误差进行排序,第一个返回结果具有较小的重投影误差。如果第二个结果的重投影误差比第一个要大得多,则选取第一个解作为位姿解算结果。如果两个解的重投影误差差别不大,则面临位姿歧义的情况,仅依靠重投影误差不能判别两个可能解的正确性,事实上,由于此时重投影误差包含较大噪声,正确的位姿结果可能还具有较大的重投影误差,需要额外的约束条件来判别正确的位姿结果。
将组合二维码坐标系设定为世界坐标系(见图1),设各二维码坐标系到世界坐标系的变换矩阵为Ti w,i= 0,1,2s 。假设某张图像中检测识别到n个(n≥1)二维码,首先使用IPPE 算法对每个检测到的二维码计算相对位姿,IPPE 返回两个可能的解,记为Ti与Ti′,i∈ [0,1,2],两个解对应的重投影误差分别记为ei与ei′,i∈ [0,1,2]。
接下来使用所有检测到角点的平均重投影误差初步筛选位姿解算结果。设相机内参矩阵:

式中f x,fy分别为相机焦距,[p x,py]T为相机主点坐标。
记所有检测到的原始图像坐标系二维码角点坐标为p j,j= 0,1 ⋅⋅⋅ 4n,对应的二维码角点世界坐标为Pj,j= 0,1 ⋅⋅⋅ 4n,定义单个二维码平均重投影误差:
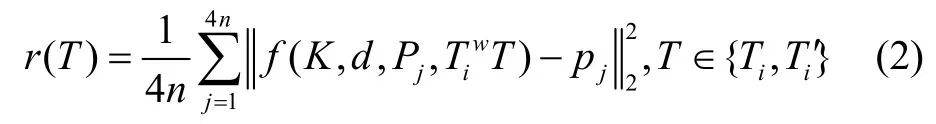
式中d=(k1,k2,p1,p2,k3)为畸变参数,f(K,d,Pj,Ti wT)使用变换矩阵Ti wT将世界坐标系3D点投影为图像坐标系2D 点。
选取使所有的3D-2D点对平均重投影误差最小的二维码位姿T*与T*′作为最优候选解算结果。
2.2.3 位姿歧义校正
比 较最 优 候选位姿T*与T*′对 应的e*与e*′,令σ=e*′ /e*。当σ≥5.0(较大阈值)时认为位姿解算结果没有歧义,否则进行位姿歧义校正。本文提出了引入机载IMU 水平姿态约束进行二维码位姿歧义校正算法。
如图4(a)所示,设最优候选位姿对应二维码中心在图像平面的投影为pm:

式中pi,i∈ [0,1,2,3]为原始图像坐标系的二维码亚像素角点坐标。
设过相机光心的铅垂线在图像平面的投影点为pv,使用北东地(NED)坐标系下过光心的铅垂线上一点V= [0,0,1]T求取pv。
相机与IMU 的坐标轴定义与安装关系如图4(a)所示,相机与铅锤面的夹角为30 °,则IMU 到相机的方向余弦矩阵为:

式中,R(·)为旋转矩阵。
设 IMU 的滚动角为φ,φ∈[ -π,π],俯仰角为θ,θ∈ [ -π/ 2,π/2],航向角为ψ,ψ∈[ -π,π],则北东地坐标系到IMU 的方向余弦矩阵为:
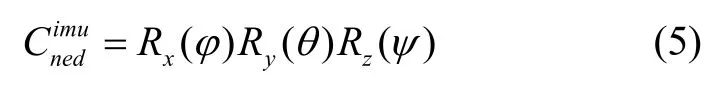
式中,R(·)为旋转矩阵。
点V在相机坐标系下的坐标V′为
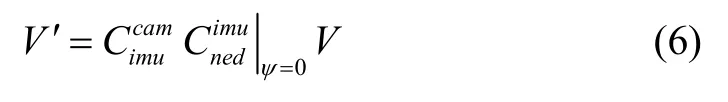
由于算法只关心IMU 提供的水平姿态,不依赖其航向角,因此,计算时可将ψ置为零,所以本文歧义校正算法不依赖于GPS 信息且消费级别的IMU 即可满足算法需求。
点V在图像平面的投影点pv为:

式中K为相机内参矩阵,d为相机畸变参数,repj()表示投影变换,将相机坐标系3D 点投影到图像坐标系2D 点。需要说明的是投影点pv坐标值可以超出图像边界而不影响后续计算结果。
点p m,pv的俯视示意图如图4(b)所示(以2#码为例)。记二维码坐标系x轴与二维码边线交点的图像坐标为px,y轴与二维码边线交点的图像坐标为py,则:

记图像坐标系中x轴与y轴向量为:


式中·符号表示向量点积。
将二维码位姿矩阵分解为旋转与平移两部分:
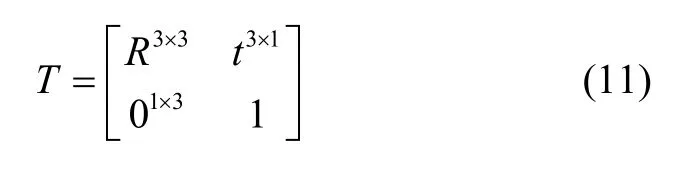
则相机在二维码坐标系下的平移向量可表示为tc=-RTt= [tx,t y,tz]T。由着网回收场景硬件配置可知,二维码在相机视野中时tz≥ 0恒成立。利用p m,pv的相对坐标关系即cosα,cosβ的符号可以确定t x,ty的符号,进而可以从T*与T*′中选取正确的位姿解。
由图4(b)中所示点pv与点pm的坐标关系可知,cosα> 0,cosβ< 0。设T*与T*′对应的相机在二维码坐标系下的平移向量分别为t c与tc′,t c与tc′ 的坐标分布如图5(a)中所示,tc位于第四象限,tc′位于第二象限。由cosα> 0,cosβ< 0可知真实的平移向量位于第四象限,则与tc对应的T*为正确的位姿结果。
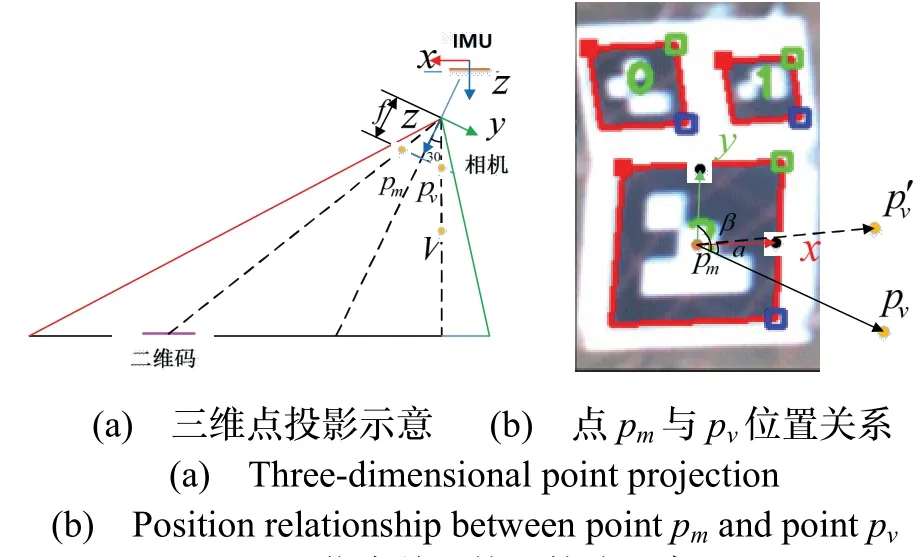
图4 位姿歧义校正算法示意图Fig.4 Pose ambiguity correction
由于IMU 精度限制和相机IMU 安装误差等原因,存在这样的情况:相机在二维码坐标系下的平移t c与tc′某个轴的分量值非常小,如图4(b)中pv′点所示。pv′点y轴坐标值接近于零,其值可能主要由误差组成,导致计算值与真实值反号,如图5(b)所示。这时t c与tc′ 均不满足 IMU 约束条件,需要特殊处理。选取cosα,cosβ中绝对值较大的一个,优先保证与其对应的坐标轴分量,放宽另一个轴的符号使其满足最接近的真实解。

图5 通过IMU 约束选取正确结果示意图Fig.5 Select the correct pose through IMU constraints
2.2.4 L-M 位姿优化
经过位姿解算与歧义校正步骤获取了正确的组合二维码位姿解算结果,为了充分利用所有检测到的二维码信息,利用所有二维码角点构建位姿优化问题,对IPPE 解算结果进行微调。Levenberg-Marquadt[15]性能优异,是常用的非线性优化方法,本文使用L-M 算法进行位姿优化。
设检测识别到二维码个数为n,记所有检测到的原始图像坐标系二维码角点坐标为p j,j= 0,1 ⋅⋅⋅ 4n,对应的世界坐标为Pj,j= 0,1 ⋅⋅⋅ 4n,经过位姿解算与歧义校正得到的初始位姿解为T*,位姿优化的目标函数为:

式中K为相机内参矩阵,d为畸变参数,i为T*对应的二维码ID,f(K,d,Pj,Ti wT)将世界坐标系3D点投影为图像坐标系2D 点。
在实际应用中,由于可能存在异常二维码识别的情况,将导致优化中存在一条误差很大的边,它的梯度也很大。如果对这种错误的边不加限制,将会导致整体优化结果偏向于误匹配的边,导致优化结果失败。本文使用Huber 鲁棒核函数解决这个问题:

可以看到,当误差e>δ时,误差函数增长由二次形式变为一次,有效地限制了梯度的最大值,同时,Huber 核函数又是光滑的,便于求导。
3 实验验证
3.1 实验设置
以大疆经纬M600 Pro 旋翼无人机为飞行载体,搭载英伟达Jetson TX2 嵌入式平台、Bobcat1921 可见光相机、SBG Ellipse-D IMU 和OEM615 卫星接收机等对本文算法进行实验验证。可见光相机最大分辨率为1920 ×1080,顺时针旋转90 °安装,其全局快门(Global shutter)设计有利于高速飞行时图像采集,相机镜头焦距f=8mm,实验时F 数(F No.)设为4。组合二维码由PP 板打印安装并放置于实验场地地面,二维码上方设置红色回收网以模拟回收平台。算法定位精度使用差分卫星(DGPS)接收机来评价,差分接收机由机载OEM615 移动站和地面OEM615 基站组成。

图6 实验无人机平台及回收硬件设置Fig.6 Experimental UAV platform and recycling setup
3.2 定位精度分析
定位精度如图7所示,“DGPS”曲线表示差分GPS定位结果,为定位真值,“OpenCV-PnP”曲线表示使用OpenCV 库solvePnP 函数解算结果,“Our-IPPE”曲线表示使用去除位姿歧义校正步骤的位姿解算流程计算结果,“Our-IPPE-disambiguation”曲线表示添加位姿歧义校正步骤后计算结果。

图7 定位精度曲线Fig.7 Positioning accuracy curve
由图7可知(时间区间[28585,28605]秒无人机飞越二维码合作目标,二维码不可见)“OpenCV-PnP”方法解算结果在x,y,z轴方向上均出现了大的坐标值反转(歧义),并在x轴分量上有许多小的坐标值歧义存在;“Our-IPPE”方法消除了大部分的小尺度坐标值歧义,但是仍旧含有大的坐标歧义存在;由“Our-IPPE-disambiguation”曲线可知,在添加位姿歧义校正步骤后有效地杜绝了各坐标轴方向上的解算歧义,实现了无人机定位结果的平滑与大幅精度提升。
为了对定位精度进行量化分析,引入绝对轨迹误差(Absolute Pose Error,APE)根据时间差直接测量真实轨迹和估计轨迹点之间的差异。统计其均方根误差(Root Mean Square Error,RMSE)、平均误差(Mean)、中值(Median)、标准差(Std)、误差最小值(Min)和最大值(Max)等,各误差统计数据见表1。
由误差统计结果可知,由于位姿解算歧义的存在,“OpenCV-PnP”与“Our-IPPE”方法具有非常大的误差最大值,在破坏位姿解算连续性的同时导致多项误差统计指标增大;“Our-IPPE-disambiguation”在标准差和均方根误差等多项结果中均具有最小定位误差,在整个无人机回收实验过程中取得了0.245 m 的标准差与0.022 m 的最小定位误差,具有非常好的定位结果。

表1 各方案定位误差统计(单位:m)Tab.1 Positioning error statistics (unit: m)
使用本文提出的“Our-IPPE-disambiguation”完备位姿解算与歧义校正方案在多架次飞行实验中的定位数据统计如表2所示。可以看出,三架次飞行实验导航作用距离均大于30 m,回收全过程标准差均0.3 m左右,最小定位误差仅为0.02 m 左右,定位精度完全满足无人机动平台着网回收控制需求,且各飞行架次定位结果差异不大,证明本文提出的导航算法具有较好的鲁棒性。

表2 多架次数据统计(单位:m)Tab.2 Multiple flight data statistics (unit: m)
4 结 论
本文针对无人机动平台着网回收应用场景,提出了一套基于二维码合作目标的惯性/视觉位姿歧义校正解决方案。设计了易于远距离辨识的9 位编码防遮挡方形二维码序列,并将0#与1#二维码抬起一定角度构建了非共面组合二维码,用于优化相对位姿解算与位姿歧义问题。通过二维码角点坐标优化、IPPE 位姿解算、位姿歧义校正和L-M 位姿优化等步骤实现了快速鲁棒位姿解算与歧义校正。室外多架次飞行实验表明本文方法相较于OpenCV 库与原生IPPE 算法消除了位姿解算歧义,提升了定位精度与鲁棒性,导航作用距离大于30 m,回收末段最小定位误差仅为2 cm左右,完全满足无人机动平台着网回收控制需求,具有较好的应用前景。

