基于因子图的船用导航系统信息融合算法
张崇猛,邓福建,杨 涛,兰晓阳
(1.中国船舶航海保障技术实验室,天津 300131;2.天津航海仪器研究所,天津 300131)
舰船导航系统通常包括捷联惯性导航系统(SINS)、北斗(BD)、多普勒(DVL)和天文导航(CNS)等,其中任何单一导航设备都具有一定的局限性,而相互之间输出信息又具有冗余性和互补性。为满足舰船长期航行中高精度和高可靠性的要求,有必要进行多源融合组合多导航设备的量测信息,克服单一导航设备存在的不足,提高导航系统的可靠性。对于多源导航信息融合算法,目前常用的有联邦滤波和因子图等[1]。国内外学者对联邦滤波的研究起步较早,已取得丰硕的成果,如文献[2]利用混合粒子联邦滤波方法,解决具有非线性系统的组合导航信息融合问题,文献[3]设计一种自适应联邦滤波算法,并基于支持向量机设计一种故障检测隔离算法,提高组合导航的稳定性。联邦滤波算法通常要求各导航设备连续工作且具有相同的信息更新频率。然而舰船众多导航设备通常具有不同的信息更新频率,且各导航设备的可用性随环境动态改变,如舰船在深水域航行时多普勒计程仪(DVL)无法测得绝对速度,北斗导航系统(BD)和天文导航系统(CNS)的可观测星数目受环境影响等,这些情况使得联邦滤波需要频繁调整融合周期和架构,增加组合导航系统设计的复杂性,使组合导航系统的灵活性和可扩展性降低。
文献[4]针对自主水下航行器(AUV)异步传感器的信息融合问题,提出一种基于因子图的多源信息组合导航算法,实现连续稳定的输出导航结果。文献[5]针对地面车辆在GNSS 拒止环境下精确导航定位的需求,提出基于因子图的即插即用融合算法,快速组合可用量测信息获得健壮的导航性能。文献[6]提出一种基于因子图的异步信息融合算法,应用于无人定翼机种,满足各种条件下多源信息融合的需要,获得精确可靠的定位结果。文献[7]采用卫导输出的伪距、伪距率构建惯导/卫导因子图组合模型,利用信息矩阵的稀疏性进行优化求解以满足实时性的要求。文献[8]针对微型无人机中多导航设备信息更新频率不同和导航设备非线性问题,提出基于因子图的信息融合算法,并搭建试验系统验证算法的有效性。文献[9]采用贝叶斯树的增量推理因子图算法,自适应判断需要迭代优化的节点数量,提高计算效率。因子图通过把导航设备量测信息抽象为因子节点,用图模型描述融合问题,提供一个统一的导航设备接口和融合算法以适应各种复杂环境。目前关于因子图组合算法的研究正在逐步深入,在因子图组合算法中当某个导航设备出现故障时如何进行容错设计还缺乏研究。
综上,针对船载导航设备信息更新频率不同和可用性随环境动态改变问题,本文设计一种基于因子图的船用导航系统信息融合及容错算法,实现不同类型导航设备的即插即用和异步信息融合;采用增量平滑算法,利用先前步骤的计算结果,减少计算量;设计基于因子图的容错算法,并用于导航设备的故障检测,避免故障信息污染组合导航系统。最后开展数值仿真和半实物车载试验验证所提算法的有效性。
1 船用导航系统信息融合因子图架构
基于捷联惯性导航系统(SINS)、北斗(BD)、多普勒计程仪(DVL)和天文导航(CNS)的船用导航系统因子图融合架构如图1所示。图中惯性测量单元因子节点fIMU连接相邻时刻的导航状态变量节点,北斗因子节点fBD、多普勒计程仪因子节点fDVL和天文导航因子节点fCNS分别经故障检测与隔离模块(FDI)与相应时刻导航状态变量节点和系统误差变量节点连接,同时,系统误差因子节点ferr连接相邻时刻的系统误差变量节点,因子图模型随量测信息的不断接入而拓展。
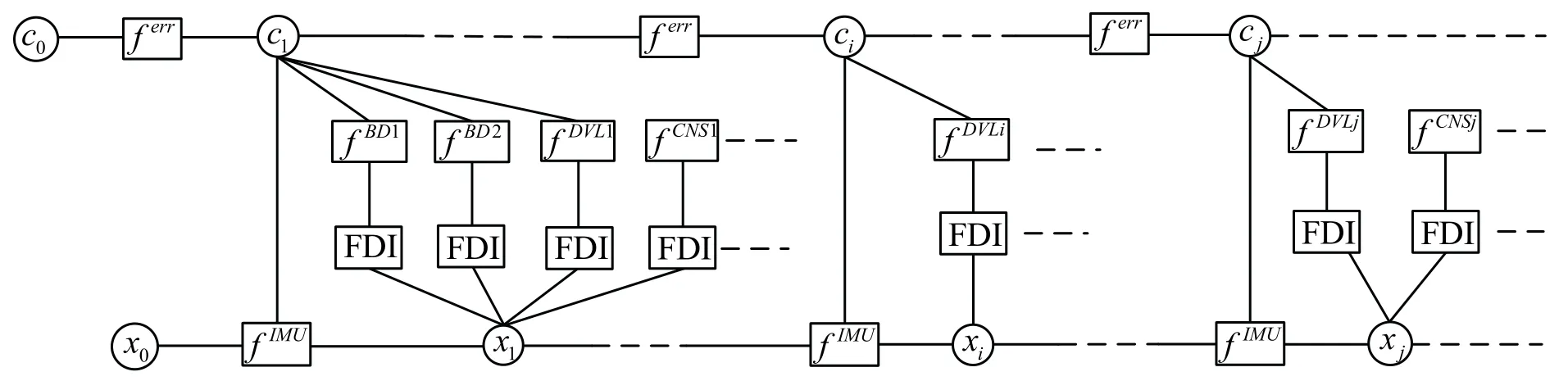
图1 基于因子图的船用导航系统融合架构Fig.1 Integrated architecture of ship navigation system based on factor graph
定义ti时刻的导航状态变量为xi和各导航设备的系统误差变量为ci,其中导航状态变量xi包括载体的姿态四元数、速度和位置,即xi=[qiViPi]T,系统误差变量包括陀螺常漂εn和加速度计常偏 ∇n、北斗接收机钟差δtu和钟漂δtf、多普勒计程仪刻度系数误差δk。定义从初始时刻t0到当前时刻tk的导航状态变量和系统误差变量的集合;定义从初始时刻t0到当前时刻tk的量测信息集合为其中zi为ti时刻接收到的量测信息集合,记分别表示惯性测量单元因子节点fIMU、北斗因子节点fBD、多普勒计程仪因子节点fDVL、天文导航因子节点fCNS在ti时刻的输出,则zi为集合的子集,其中北斗导航系统的量测为伪距、伪距率,多普勒计程仪的量测为速度,天文导航的量测为高度角。
惯性测量单元因子节点可表示为:
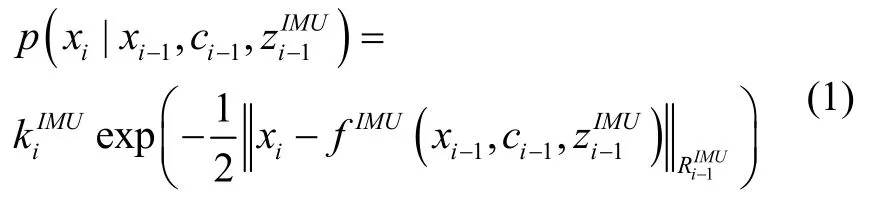
式(1)中,fIMU表示导航状态运动方程,导航状态之差只是形式上的表式,对于姿态四元数,具有乘性性质。表示马氏距离,表示惯性测量单元的测量噪声误差协方差矩阵,表示归一化系数。
系统误差因子节点可表示为:
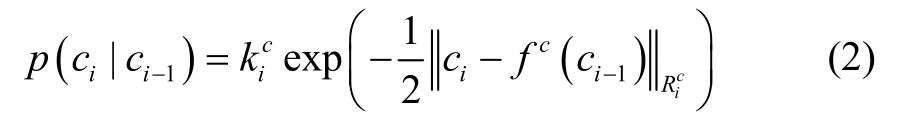
式(2)中fc表示系统误差传递规律方程,Ric表示系统误差的估计误差协方差矩阵。
根据载体连续时间运动微分方程:
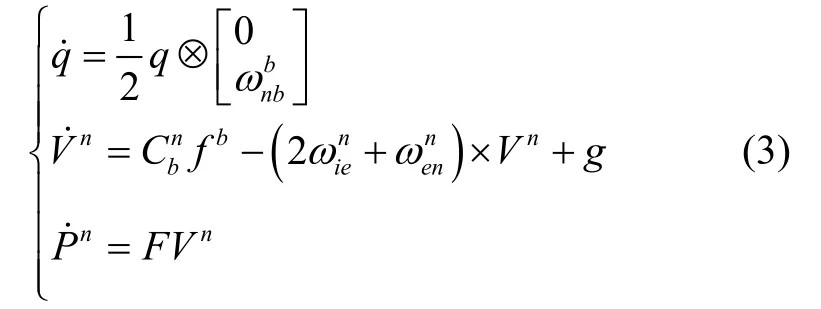
式中,C bn为b系到n系姿态转换阵,ω ie为地球自转角速度,R M、R N分别为舰船位置点处子午圈、卯酉圈曲率半径,h为当地高度,L为当地纬度。

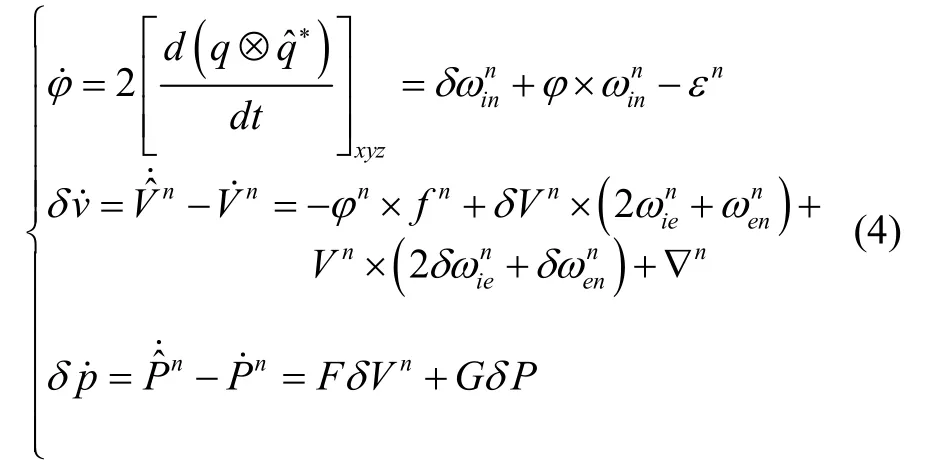
[ ˙]xyz表示只取四元数的虚部组成的三维向量,φ表示姿态角误差。
陀螺和加表随机漂移可建模如下:

式(5)中,εw和∇w分别为陀螺和加表的测量白噪声,εbn和 ∇bn为陀螺和加表随时间缓慢变化的偏置误差,满足下式:

εbw和∇bw分别为陀螺和加表偏置误差的驱动噪声。北斗接收机钟差钟漂和DVL 刻度系数误差微分方程如下:
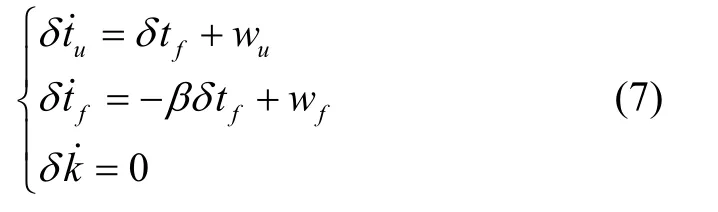
定义ti时刻误差向量
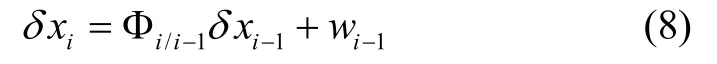
将式(3)离散化,可得载体离散时间运动方程
假设根据载体离散时间运动方程推算ti时刻导航状态估计,ti时刻导航状态估计,则IMU 因子节点残差定义为:

北斗、DVL 和天文导航因子节点具有如下形式:
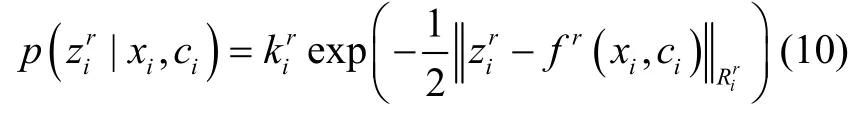
式中,r分别表示卫星无线电导航系统(RNSS),DVL和CNS;fr分别表示北斗、DVL 和天文导航的量测方程,将式(10)在导航状态变量估计值和系统误差变量估计值处作一阶泰勒展开,定义变量节点ui=[x ici],则各因子节点可表示如下:
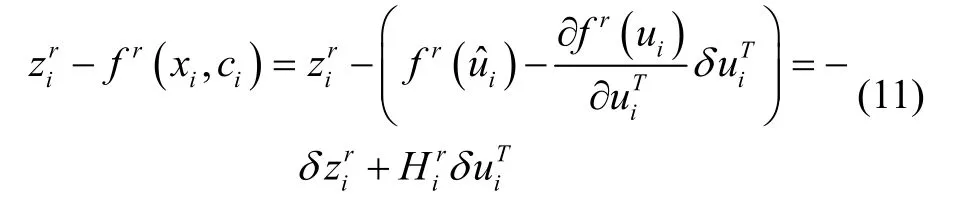
北斗第j颗卫星的伪距和伪距率量测方程为:
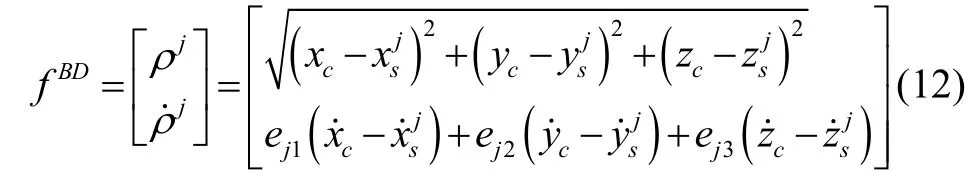
式中,xc、yc、zc和分别表示舰船在地心地固坐标系中的位置和速度,和分别表示第j颗卫星在地心地固坐标系中的位置和速度,ej1、ej2和ej3分别表示第j颗卫星到舰船的方向余弦向量。
北斗第j颗卫星的量测矩阵为:
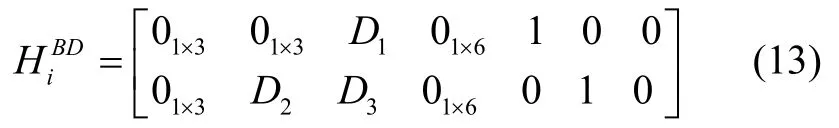
式中,各符号定义为:
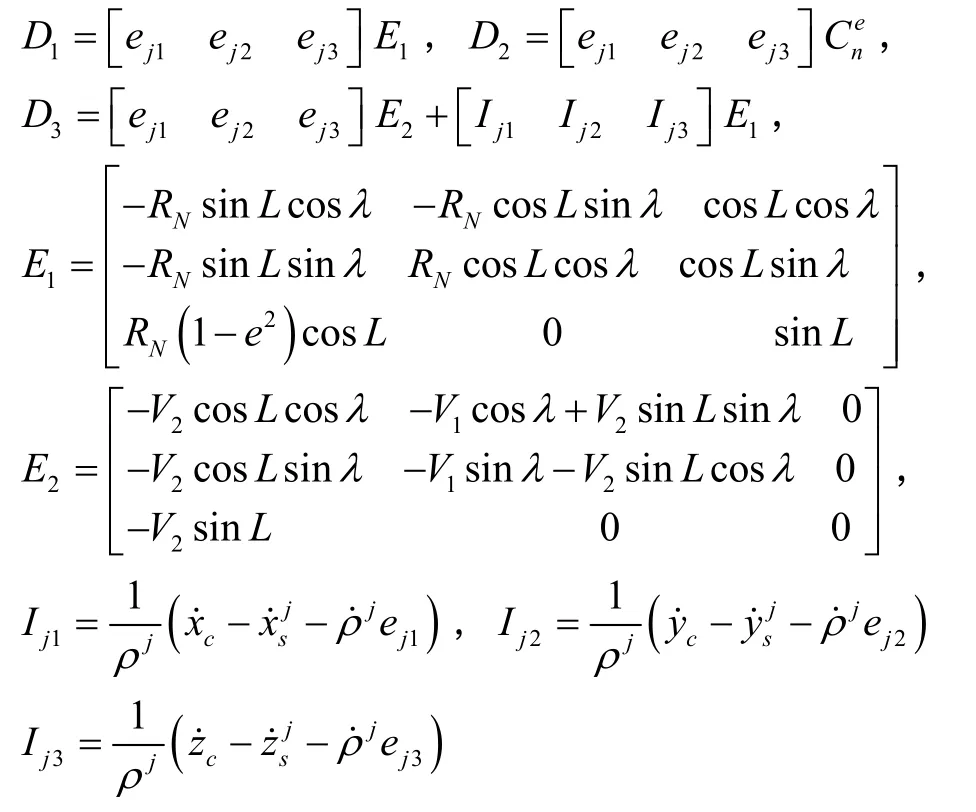
DVL 速度量测方程为:
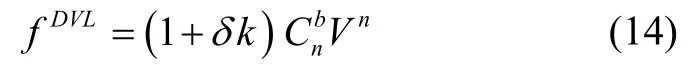
式中,δk为刻度系数误差。
DVL 量测矩阵为:

为简化三角函数运算量,以高度角的正弦值作为间接观测量。天文导航量测方程为:
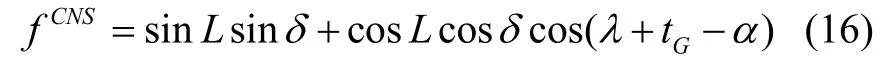
式中,α为可观测星的天球赤经,δ为天球赤纬,tG为本初子午线赤经。对于第j颗可观测星,量测矩阵如下:

式中,

综上,基于所有时刻量测信息Zk的联合概率密度函数为:

根据最大后验概率估计,各时刻导航状态和系统误差变量的最优估计值如下:
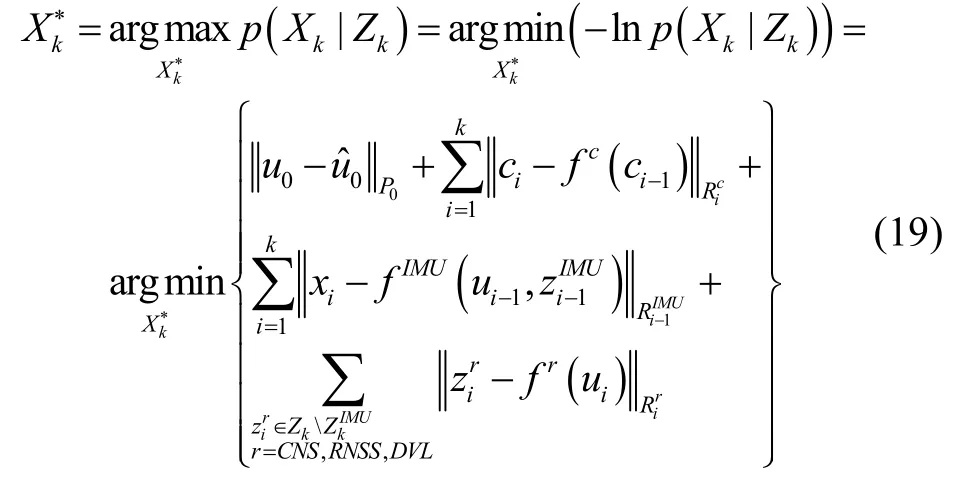
采用无约束非线性最小二乘优化理论求得式(19)的最优解,即可获得各时刻导航状态量的最优值Xk*。
2 基于因子图的信息融合算法
2.1 增量平滑融合算法
对于SINS/BD/DVL/CNS 的融合问题,每插入一个新的量测因子节点,就相当于在式(19)线性化建立的雅克比矩阵中增加一行,随着导航时间的增加,雅克比矩阵的维数也将越来越大,式(19)求解的计算量也逐渐增大。由于只有部分变量节点受新因子节点的影响[10],因此在计算过程中可重复利用先前步骤的计算结果进行增量更新。
将式(19)中马氏距离转化为2-范数,即:
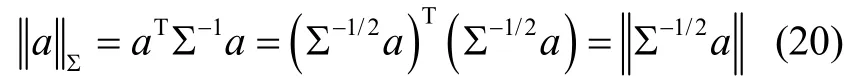
将式(19)转化为标准最小二乘的优化问题,并线性化建立雅克比矩阵J,雅克比矩阵中每一行对应因子图中的一个因子节点,如式(21)所示。
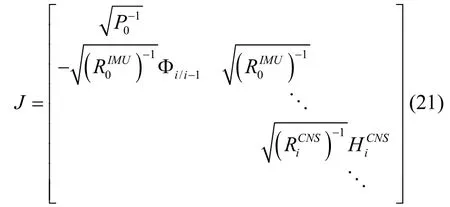
对应的右侧向量为:
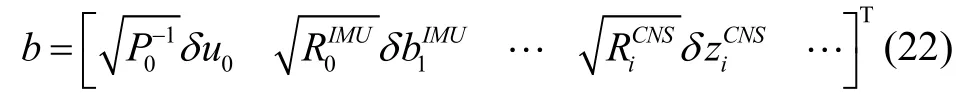
采用对联合概率密度函数进行变量消元的方式实现对雅克比矩阵J的更新,将联合概率密度函数分解为如下条件概率密度形式:
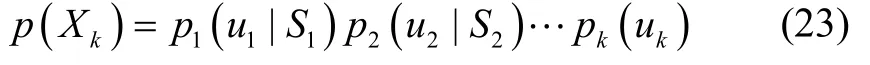
其中Si是与变量xi相关的分离器,选定变量消元顺序后,逐步对变量和其分离器采用部分QR 分解算法依次进行消元,直至将雅克比矩阵J分解为上三角形矩阵R和正交矩阵Q。当插入新的因子节点后,识别受新因子节点影响的变量节点,然后只对受影响的变量节点及其分离器进行部分QR 分解,完成受影响变量节点的消元过程。消元步骤完成后,反向回代计算受影响的变量节点的估计值。然后在更新后的状态变量估计值处重新线性化,迭代计算导航状态变量的最优值,实现导航状态变量的更新。增量更新算法如下:
1) 根据初始信息建立先验因子节点P(u0),设置变量节点初值;
2) 插入因子节点:接收到BD、DVL 或CNS量测信息时,建立相应因子节点并连接相关变量节点,接收到IMU 量测信息时建立IMU因子节点和当前时刻变量节点,并与前一时刻变量节点连接;
3) 识别受新因子节点影响的变量节点集合;
4) 根据IMU 测量信息计算新增变量节点初始估计值,并在状态变量估计值处线性化建立雅克比矩阵J和右侧向量b;
5) 采用变量消元方式求解状态变量误差估计值δui,并更新变量节点,令
2.2 容错算法
全局雅克比矩阵J经QR 分解后得到上三角形矩阵R,在矩阵R中包含有导航状态和系统误差的误差协方差信息,记∑为所有时刻导航状态和系统误差的误差协方差矩阵[11],则:

记tk-1时刻导航状态和系统误差的误差协方差矩阵为Pk-1,在R的维数较大时为减少计算量可采用回代算法计算Pk-1。假设Pk-1的维数为n,定义,则关于X的方程RTRX=B的解的最后一个n×n矩阵块即为Pk-1。定义:
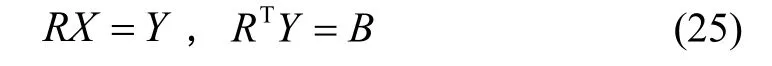
其中Y为中间过渡变量,因R是上三角矩阵,采用回代算法可快速求解未知矩阵X。
设tk时刻接收到量测信息zkr后,根据tk-1时刻的变量节点最优估计和IMU 量测进行预测,得tk时刻的导航状态变量节点预测值和系统误差变量节点预测值,可知不受量测信息zkr的影响,的估计误差协方差矩阵:
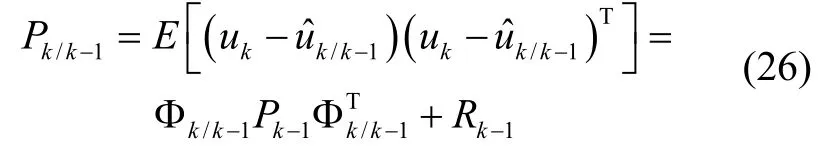
定义残差:
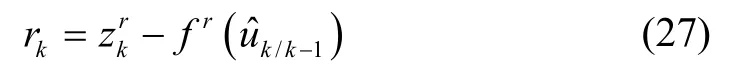
则系统无故障时残差应为零均值的高斯白噪声,残差rk的协方差矩阵为:
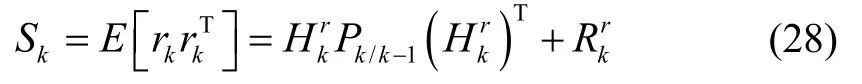
定义统计量:

则λk服从χ2分布,由奈曼-皮尔逊准则可知,当限定误警率P f=α时,可由解出使得漏检率达到最小的门限TD。则判定准则为:

故障检测与隔离模块(FDI)插入在量测因子节点和变量因子节点之间,通过式(29)计算的统计量λk和式(30)的判定准则判断新接收到的量测信息是否有故障,最后决定是否将该因子节点插入到相应的变量节点上。
3 仿真试验与分析
为了验证本文提出的基于因子图的船用导航系统信息融合及容错算法的性能,分别进行了仿真验证和半实物车载试验验证;同时采用有重置的联邦滤波算法与所设计的因子图算法进行对比。
3.1 仿真试验
设置仿真时长3600 s;IMU 更新频率为200 Hz,陀螺仪常值漂移误差0.01 °/h,角度随机游走系数;加速度计常值漂移误差100 µg,速度随机游走系数;北斗更新频率1 Hz,伪距测量噪声均方根值2 m,接收机钟差等效测距误差300 m,伪距率测量噪声均方根值0.1 m/s;DVL 更新频率10 Hz,刻度系数误差0.001,速度测量噪声误差均方根值0.1 m/s;天文导航更新频率2 Hz,高度角测量噪声均方根值10 "。由于在复杂导航环境下,DVL因工作环境限制易发生间断性失效,北斗和天文导航易受环境和天气影响;捷联惯导是一种自主导航系统,且惯导本身可以采用余度技术提高可靠性,因此设置各导航设备工作状况如表1。分别采用因子图算法和有重置联邦滤波算法对SINS/BD/DVL/CNS 进行信息融合,仿真结果如图2~4,导航参数误差以及定位误差(径向误差)的均方根值(RMS)如表2所示。
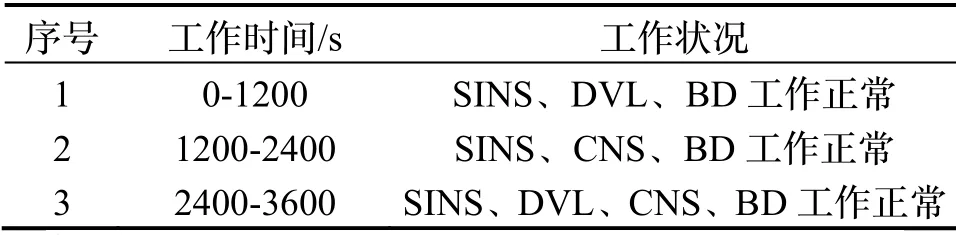
表1 各导航设备工作状况Tab.1 Working condition of each sensor

图2 因子图与联邦滤波的姿态误差角对比曲线Fig.2 Comparison on attitude errors between factor graph and federated filter
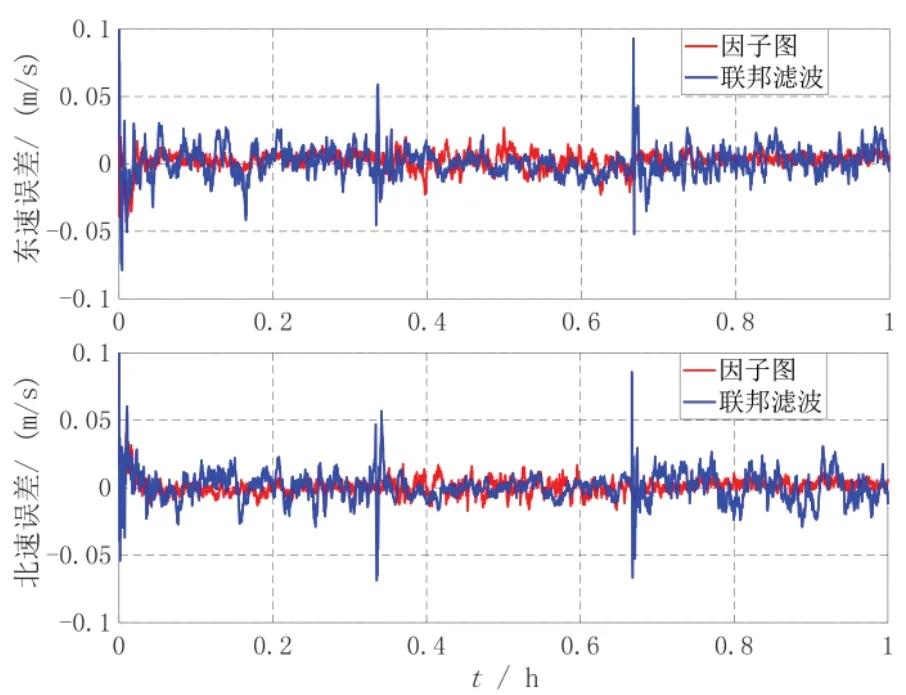
图3 因子图与联邦滤波的速度误差对比曲线Fig.3 Comparison on velocity errors between factor graph and federated filter
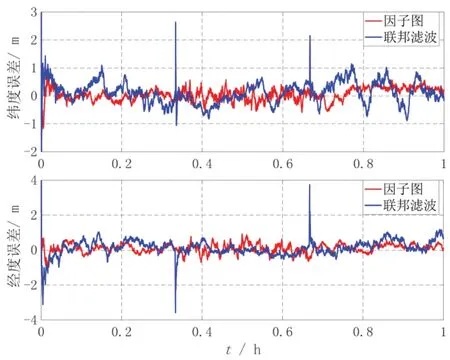
图4 因子图与联邦滤波的位置误差对比曲线Fig.4 Comparison on position errors between factor graph and federated filter

表2 因子图和联邦滤波算法定位性能比较Tab.2 Comparison of location performance between factor graph and federated filter algorithm
由图2~4 的误差曲线可以看出,因子图与联邦滤波都能保持较高的定位精度,位置误差收敛在5 m 以内,速度误差收敛在0.1 m/s 以内,姿态误差收敛在1ʹ以内,具有较好的融合精度。
船用导航系统通常采用高精度导航设备,可近似视为线性系统。由于因子图算法是一种最小残差优化算法,对于线性系统,联邦滤波是一种最小化状态误差协方差矩阵的估计算法,在理论上因子图算法和联邦滤波算法具有相当的导航精度。对比表2中导航参数误差的均方根值,因子图姿态估计精度稍优于联邦滤波,因子图的定位误差为0.74 m,联邦滤波的定位误差为0.88 m,速度误差均为0.01 m/s,可知因子图与联邦滤波导航定位精度相当。
联邦滤波由于需要调整融合周期而舍弃部分量测信息,而因子图可将全部量测信息作为因子节点插入到图中,因为姿态为间接观测量,误差估计较慢,因子图通过引入更多速度量测信息而具有稍高的姿态估计精度,速度和位置为直接观测量,误差能够快速校正,更高频率的速度更新对精度影响不大,仿真验证结果和理论分析一致。
联邦滤波需要通过主滤波器对各子滤波器的信息进行融合,然后再根据信息分配原则将主滤波器的全局估计重新分配给各子滤波器,使得联邦滤波的融合周期为各子滤波器融合周期的最小公倍数,当导航设备可用性动态改变时,联邦滤波需要根据当前可用的导航设备进行系统重构。因子图算法则是在任一时刻接收到导航设备的量测信息时建立相应的量测因子节点,并将该量测因子节点插入到相应时刻的变量节点上,同时对更新后的因子图进行优化求解,实现多导航源的信息融合。因此,因子图算法具有异步信息融合和导航设备可用性动态改变时的即插即用能力,可根据导航设备的可用性增减相应因子节点,在保证与联邦滤波导航精度相当的前提下提高系统的灵活性和扩展性,满足复杂环境下的导航信息融合。
为验证所设计容错算法的性能,对各导航设备设置如表3所示故障,进行仿真验证。仿真结果如图5~6所示。

表3 各导航设备故障设置Tab.3 fault settings of each sensor
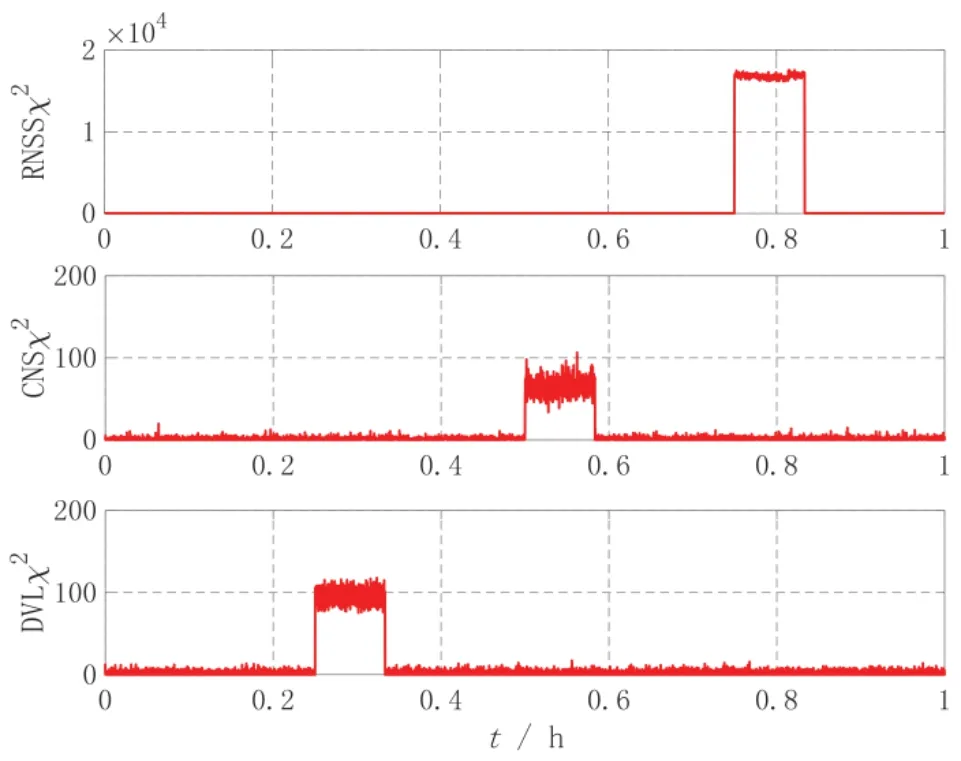
图5 χ 2统计量曲线Fig.5 χ 2statistics curve
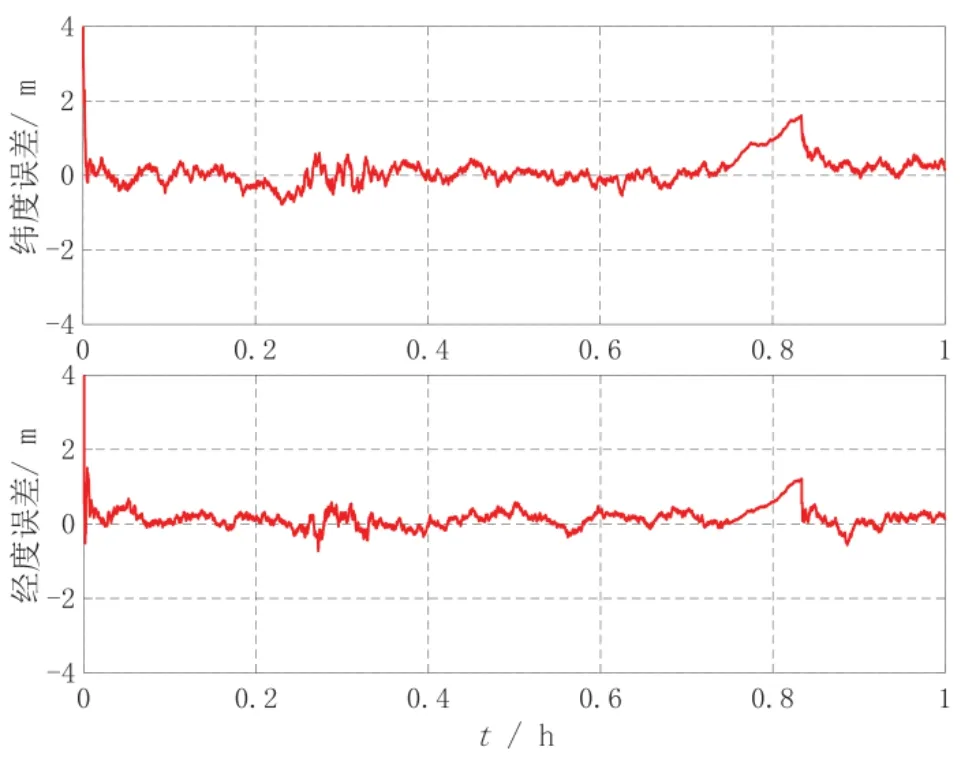
图6 因子图位置误差曲线(导航设备有故障)Fig.6 Position errors based on factor graph(multi-sensor with fault)
由图5可知,当某个导航设备发生故障后,χ2统计量迅速增大,本文所设计的基于因子图的容错算法能够有效识别出发生故障的导航设备,进而将故障导航设备进行隔离。从图6可以看出,带有故障的量测信息已被隔离,组合导航系统不受故障导航设备的污染,使位置误差保持在5 m 以内。
3.2 半实物车载试验
为进一步验证所设计的基于因子图的融合与容错算法的性能,开展跑车试验。因受跑车试验条件限制,开展惯导、白光测速仪和北斗的融合进行试验验证。试验以诺瓦泰差分接收机输出的速度位置作为参考信息,输出频率为1 Hz;并同步采集惯导、北斗和白光测速仪的数据,其中惯导输出频率100 Hz,白光测速仪输出频率10 Hz,北斗输出频率1 Hz。设置在1200-2400 s 白光测速仪不可用,运用因子图算法和联邦滤波算法分别对惯导/北斗/白光测速仪进行信息融合,得融合结果如图7、图8和表4所示。
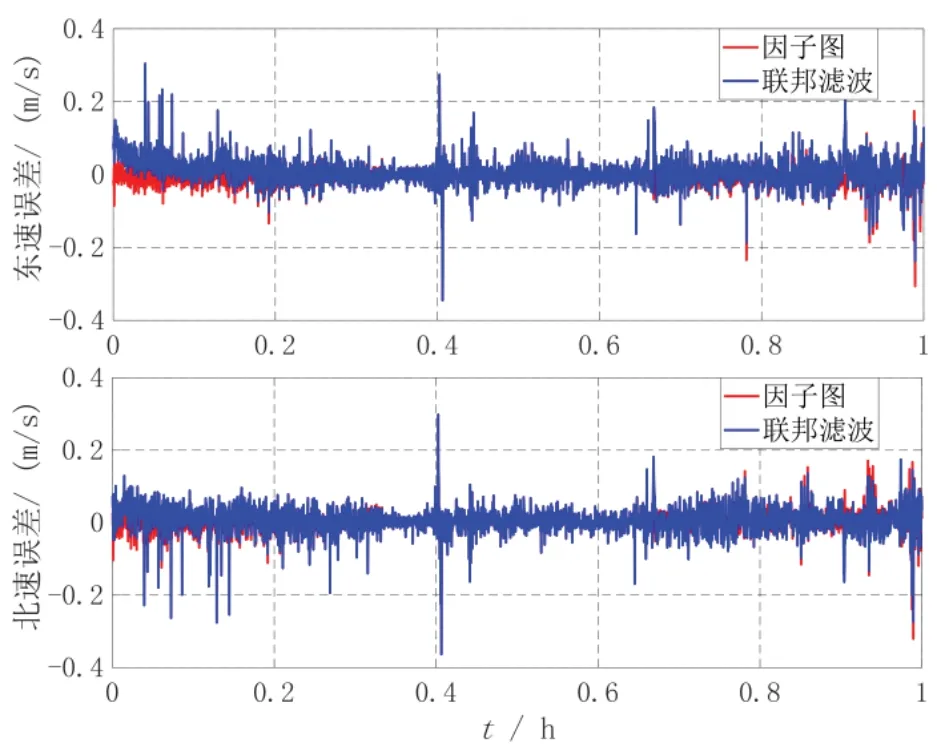
图7 因子图与联邦滤波的速度误差对比曲线Fig.7 Comparison on velocity errors between factor graph and federated filter

图8 因子图与联邦滤波的位置误差对比曲线Fig.8 Comparison on position errors between factor graph and federated filter
从图7、图8可以看出,因子图和联邦滤波水平定位误差在5 m 以内,速度误差在0.1 m/s 以内;由表4可知,因子图算法的定位误差为0.79 m,联邦滤波定位误差0.80 m,可知因子图与联邦滤波导航精度相当,半实物车载试验结果与上节仿真验证结果一致。但在导航设备工作状态发生改变时,联邦滤波需要重构,因子图算法可通过增减相应导航设备的因子节点实现,具有更好的异步信息融合和即插即用能力,组合系统具有更强的灵活性和扩展性。

表4 因子图、联邦滤波算法定位性能比较Tab.4 Comparison of location performance between factor graph and federated filter algorithm
为验证所提因子图容错算法,在900-1200 s 北斗注入定位误差 200 m,速度测量误差 0.3 m/s,2100-2400 s 白光测速仪注入测量定位误差3 m/s,验证因子图容错算法的性能。结果如图9和图10 所示。
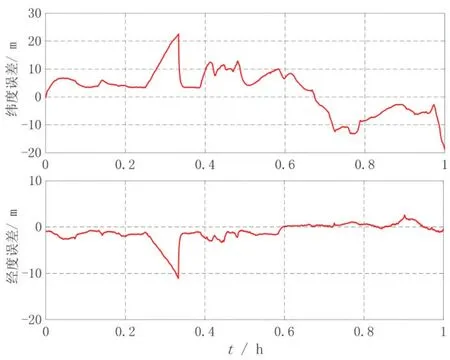
图9 因子图位置误差曲线(导航设备有故障)Fig.9 Position errors based on factor graph(multi-sensor with fault)
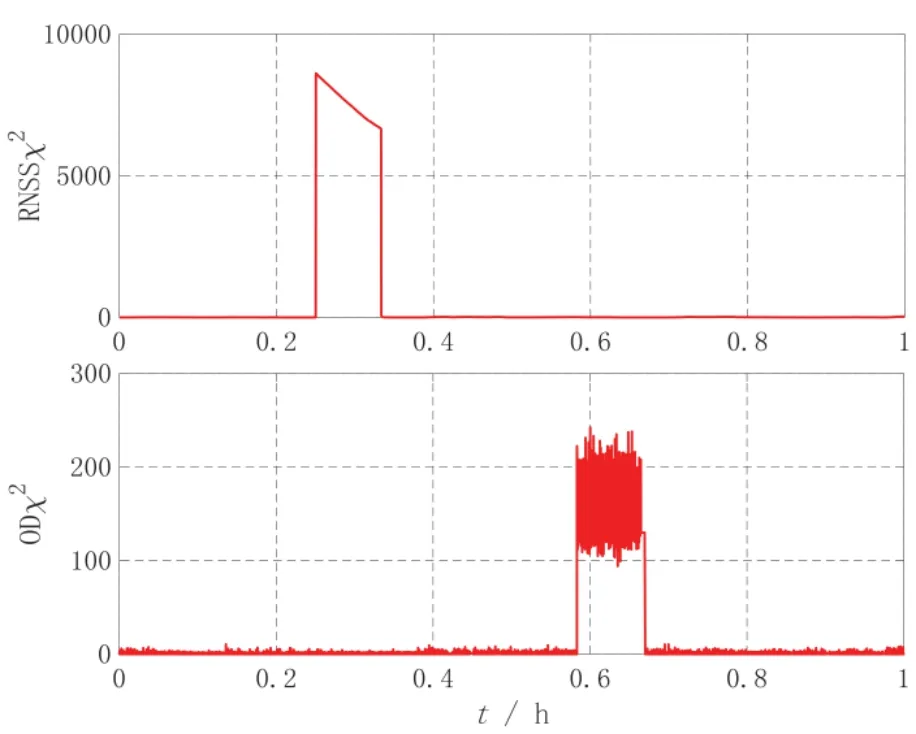
图10 χ 2统计量曲线Fig.10 χ 2statistics curve
从图9和图10 可知,当导航设备发生故障后,所设计的容错算法能够有效识别和隔离故障导航设备信息,使组合系统不受污染,并利用无故障导航设备信息进行定位,保持高精度的导航定位。
4 结 论
本文针对舰船导航系统的不同导航设备之间异步的信息更新频率以及可用性随环境动态改变的多源融合问题,提出一种基于因子图的融合与容错组合导航方案。设计基于SINS/BD/DVL/CNS 因子图融合与容错模型,并与有重置联邦滤波器的导航性能进行对比。该方法与有重置联邦滤波的导航精度相当,但却可以灵活组合异步量测信息,以及在导航设备随环境发生可用性动态改变时实现即插即用,有效实现船用导航系统的信息融合;同时实现对导航设备进行故障检测和隔离,保证组合导航系统不受故障导航设备的影响。最后,通过开展数值仿真和半实物车载试验,验证本文所提算法的有效性。

