基于因子图的无人机集群分布式协同导航方法
陈明星,熊 智,2,刘建业,2,王 融,2,熊 骏
(1.南京航空航天大学自动化学院导航研究中心,南京 211106;2.先进飞行器导航、控制与健康管理工业和信息化部重点实验室,南京,211106)
近年来,无人机集群技术得到了行业内的广泛关注,与单个无人机相比,无人机集群通过无人机之间的信息交互、相互协作能够完成更加复杂多样的任务,拥有功能分布化、体系生存率高、效率高等优势,具备极大的潜在应用价值[1-3]。
在无人机集群飞行过程中,高精度的位置信息是高效可靠地执行各项任务的关键所在。对于密集集群无人机系统来说,使用的无人机一般为旋翼飞行器,受到成本和载荷的限制,为所有无人机配备高精度导航设备是非常困难的[4]。因此,可通过无人机之间信息交互进行协同导航,从而提升无人机群的定位精度[5-8]。
国内外学者对无人载体协同导航进行了针对性的研究。文献[9]提出一种融合惯性、磁力计、可用卫星伪距、合作无人机位置、单目相机信息的协同导航方法,有效提高了无人机群在GPS 受限情况下的导航性能,但所使用的传感器数量较多。文献[10]提出了一种基于集成超宽带(UWB)和GNSS 的车载协同定位方案,能获得比分米级更好的定位精度。文献[11]提出了一种混合式协同定位方法,结合卡尔曼滤波和置信传播算法的优势,实现了无人载体网络的协同定位。文献[12]提出了一种基于因子图和积算法的多AUV协同导航方法,试验结果表明其定位精度优于EKF 和UKF 算法,但其是一种集中式的处理方法。
本文提出了一种基于图优化的密集集群无人机分布式协同导航方法,结合无人机自身的GNSS 信息和无人机之间的距离信息建立了协同导航因子图,并通过消息迭代实现了因子图的分布式处理,最后通过仿真验证了所提出方法的有效性。
1 集群无人机协同导航方案
在密集集群的情况下,为了防止无人机之间发生碰撞,无人机的位置精度显得尤为重要。Real-time kinematic (RTK) 载波相位差分技术虽然能达到厘米级的定位精度,但为集群中所有无人机全部配备RTK设备的成本太高。本方案中,为了获得更高的定位精度,为少量无人机配备高精度RTK 设备,其他无人机配备普通的卫星导航设备,在飞行过程中,无人机可通过数据链与相邻无人机进行信息的交互,进而实现协同信息的融合与定位结果的优化。协同导航方案如图1所示。
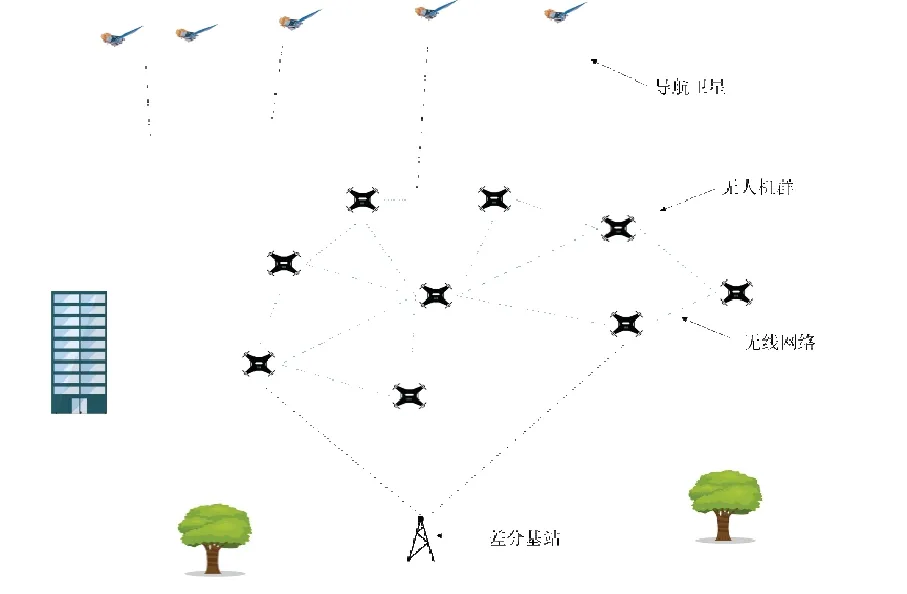
图1 无人机群协同导航方案Fig.1 Cooperative navigation scheme for UAV swarm
2 基于图优化的协同导航方法
2.1 系统模型与问题描述
假设所有无人机可通过卫星导航设备接收到自身的位置信息,同时可以跟相邻的无人机进行信息交互。x表示无人机的位置状态,可定义集群无人机的位置变量为:
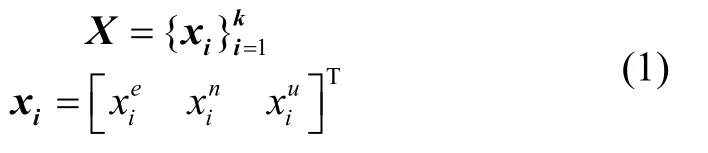

其中,Z为无人机群接收到的所有量测值,包括GNSS信息和无线测距信息。由此可得位置变量X的最大后验估计为:
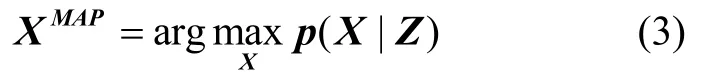
以图2所示的6 架无人机为例,对各无人机的空间相关性进行建模,可以得到如图3所示的因子图模型。因子图是一种双边图,其包含两种类型的节点:因子节点fi,j和变量节点xi。
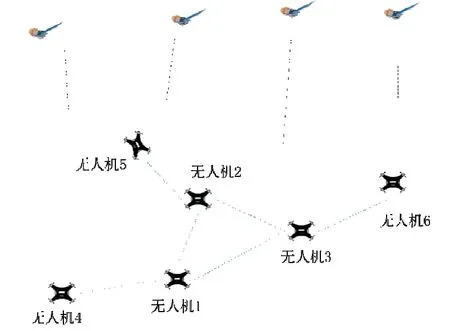
图2 无人机群协同示意图Fig.2 Diagram of cooperative navigation for UAV swarm
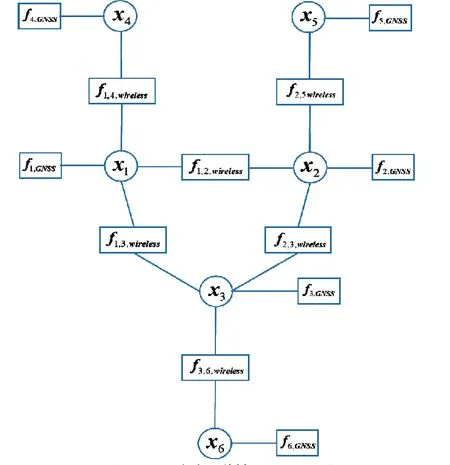
图3 无人机群协同因子图Fig.3 Cooperative factor graph for UAV swarm
根据文献[13]和文献[14],可以得到:
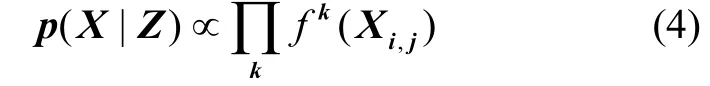
式中,Xi,j表示变量集合X中与因子fk相关的变量,k为因子的编号。对于高斯噪声分布,假设每个因子fk都具备如下形式[13]:
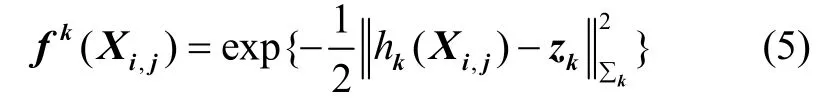
其中,hk(⋅)为测量函数,zk为真实的量测值,∑k为量测误差的协方差矩阵,为马氏距离。只需要将式(5)取对数,就可以将求最大后验估计问题转化为最小化非线性最小二乘的和的问题:
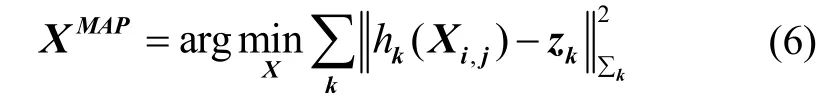
2.2 因子节点模型描述
本文中的传感器主要包括GNSS 设备和无线测距设备,本节将推导这两种传感器测量模型的因子公式。
2.2.1 GNSS 因子
对于GNSS 的位置量测,一般可建模为:
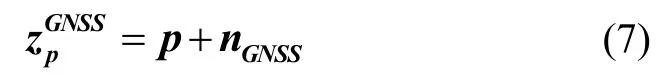
式中,p为载体的真实位置,n GNSS为GNSS 测量噪声。因此,GNSS 因子可表示为:
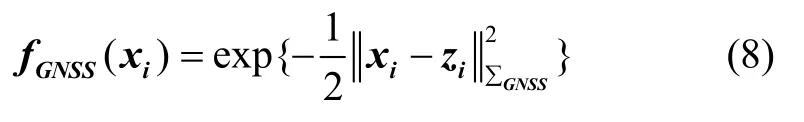
2.2.2 测距因子
无人机i和无人机j的无线测距值可建模为如下形式:

其中,di,j为i和j之间的真实距离,nwireless为测距噪声。而观测函数h(Xi,j)为:
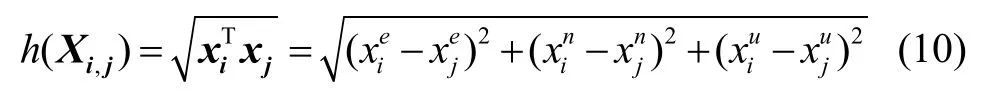
综上,测距因子可以表示为:
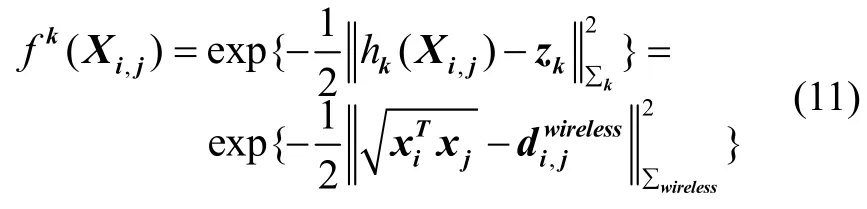
2.3 基于消息迭代策略的协同导航分布式处理方法
2.3.1 集中优化
通过泰勒展开将最小二乘目标函数线性化:
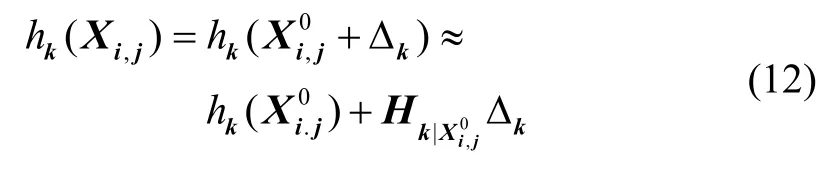
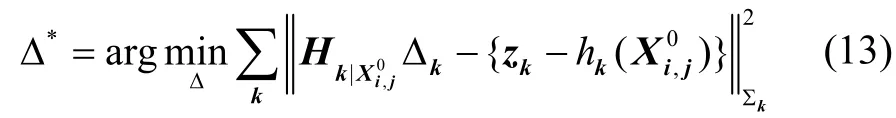
为了将不同的代价函数合并,需要对上式中的雅可比矩阵和预测误差进行“白化”,即将马氏范数转换为2-范数,从而消去观测噪声协方差矩阵∑k:
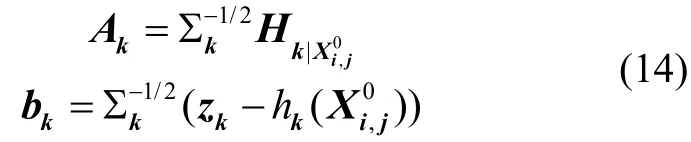
结合无人机群所有的GNSS 位置观测和无线测距值进行集中优化,得到如下标准最小二乘问题:
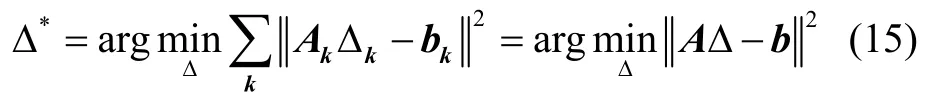
将式(15)对Δ 求偏微分并使其等于零,得到:

式(16)可通过高斯牛顿法进行求解,具体过程可参考文献[15]。
2.3.2 分布式优化
对于密集集群无人机来说,集中优化时雅可比矩阵A 的规模与无人机数量相关。假设无人机数量为n,测距信息数量为m,则A 的维数将达到(3n+m)×3n,因此,集中优化的计算量非常庞大,且非常依赖中心节点,中心节点的故障将会导致整个系统瘫痪,鲁棒性不强。
为了解决集中优化计算资源不足、过度依赖中心节点的问题,可以将2.3.1 节所述的因子图集中优化问题分散到所有无人机上进行分布式计算。每架无人机仅处理自身的GNSS 信息和相邻无人机之间的协同信息,并通过消息迭代的方式实现无人机群的位置优化,消息迭代的内容就是每架无人机的位置估计值和位置协方差。以图2中的无人机1 为例,在每次优化的初始时刻,可通过机载GNSS 设备获取自身位置信息,并利用无线网络播发位置信息和GNSS 位置量测协方差信息;当接收到相邻无人机的位置、位置协方差和距离量测之后,结合自身位置x1和相邻无人机位置x2、x3、x4可以建立局部状态、局部雅可比矩阵A1以及局部误差向量b1,从而得到如式(17)所示方程,并由此构建局部因子图。

同理可得如下方程:

通过高斯牛顿法可对x1的位置进行初步更新优化,对A1进行QR 分解A1=QR,优化后的X1的误差协方差可由式(19)求得:
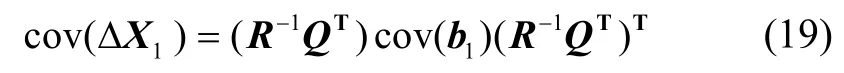
从上述误差协方差矩阵中取出相应的行和列即可获得x1的协方差。将更新后精度得到提高的位置信息及位置协方差播发出去,同时接收其他无人机播发的更新后的消息,结合自身和接收到的信息构建新的因子图,这就是消息迭代过程。重复因子图优化和消息迭代过程,直至满足迭代退出条件为止。可设置阈值来检测前后两次迭代的位置之差,以此判断是否可退出迭代。算法流程如表1所示。
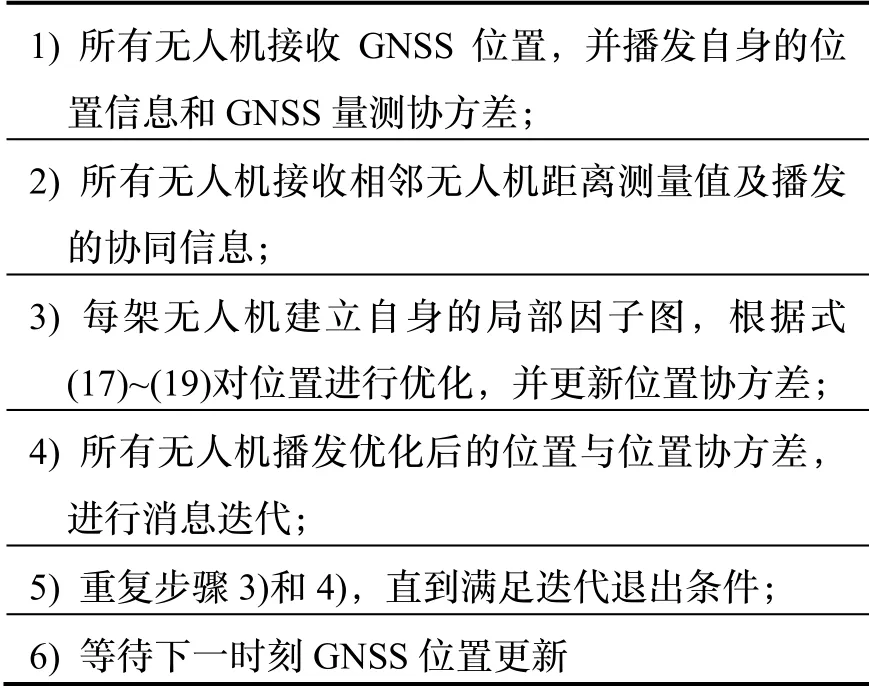
表1 基于消息迭代的协同导航分布式处理方法流程Tab.1 Process of distributed processing method for cooperative navigation based on message iteration
3 仿真分析
3.1 仿真条件设置
利用MATLAB 仿真无人机群的运动,验证算法的可行性。仿真条件如下:在200 m×100 m×200 m的范围内遍布18 架无人机,这些无人机均配备卫星导航接收机、超宽带测距模块(UWB)与通信设备,其中3 架无人机配备高精度的RTK 设备,量测噪声均考虑为高斯噪声,UWB 考虑晶振误差和信号处理时间的存在设置了晶振误差比例系数[4][5],所有无人机可与自身100 m 范围内的相邻无人机测距和通信。无人机群的初始位置如图4所示,其中一架无人机的运动轨迹如图5所示,为方便显示无人机之间的相对位置和距离,图4以(118 °,32 °,0 m)为坐标原点,三维尺度全部转化成m。表2列出了无人机所搭载设备的仿真参数。
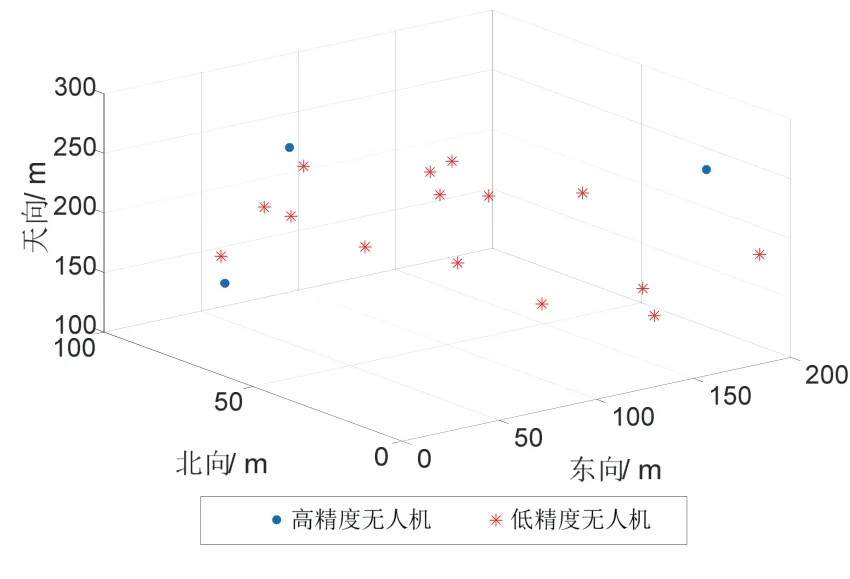
图4 无人机群初始位置Fig.4 Initial position of UAV swarm

图5 无人机1 运动轨迹Fig.5 Trajectory of UAV 1

表2 传感器配置与仿真参数Tab.2 Sensor configuration and simulation parameters
3.2 仿真结果与分析
基于上述仿真条件,对配备低精度GNSS 设备的15架无人机的定位精度进行分析。将每架无人机100m范围内的其他无人机称为可交互无人机,15 架无人机的可交互无人机个数及其中的高精度无人机个数如表3所示。
为了综合分析可交互无人机个数对优化精度的影响,选取无人机1、无人机7、无人机12 和无人机13来进行对比。对下列三种情况进行仿真,仿真结果如图6所示。
· 不进行优化而仅利用GNSS 定位;
· 仅进行一次优化而不进行消息迭代;
· 进行消息迭代优化。
蓝线表示无优化而仅GNSS 定位下的仿真结果,绿线表示仅进行一次优化而不做消息迭代下的仿真结果,红线表示迭代优化的仿真结果。

表3 可交互无人机个数Tab.3 Number of interactive UAVs


图6 定位误差对比曲线Fig.6 Comparison on position error
由图6可以看出,本文所提出的方法的定位精度相比纯GNSS 定位得到明显提升,为了定量地分析三种情况下的定位误差,对无人机定位均方根误差(RMSE)进行了统计,结果如表4所示。表4中的位置估计误差的计算公式如式(20)所示:
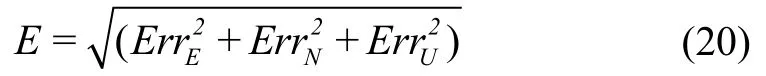
从表4可以看出,通过与相邻无人机进行信息交互和测距,可以提升无人机群的定位水平。即使在仅进行一次优化而不进行消息迭代的情况下,无人机的定位精度也得到了提高。优化后的定位精度与可交互无人机的数量存在正相关关系,对比无人机7 和无人机13 可以看出,在仅进行一次优化时,由于无人机13 存在两架高精度的可交互无人机,因此其优化效果要优于无人机7,而随着迭代的进行,可交互无人机的定位精度不断提高,无人机7 的定位精度逐渐接近无人机13 的定位精度。迭代优化后定位精度相比于未优化时无人机1、无人机7、无人机12 和无人机13分别提升了3.37、4.53、7.38、6.35 倍。
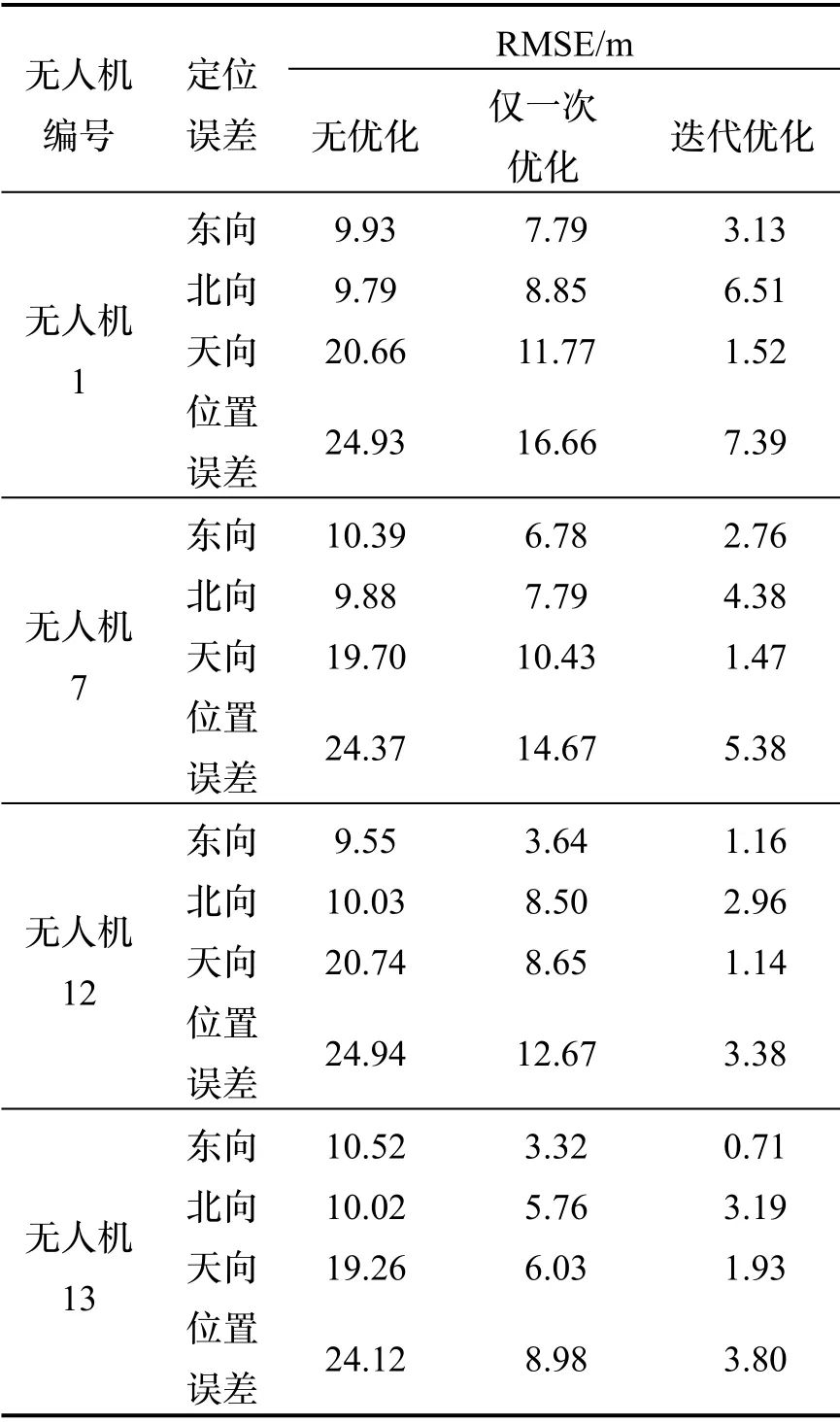
表4 定位误差统计结果Tab.4 Statistics of position error
4 结 论
本文以无人机密集集群时的协同导航为背景,研究了基于图优化的分布式协同导航方法,该方法将无人机的位置状态抽象成变量节点,将GNSS 传感器的位置量测和测距传感器的距离量测抽象成因子节点,建立了无人机群协同导航的因子图,并通过消息迭代的方式实现了因子图的分布式优化。仿真结果表明,基于图优化的密集集群无人机分布式导航方法能够实现定位解算过程的分布式处理,且可以明显地提升无人机的定位精度,减少编队中高精度导航设备的配置数量,适用于大规模无人机密集编队应用场景。本文假设量测噪声满足高斯分布,下一步将对非高斯量测噪声和相对测距存在非视距误差条件下的无人机群分布式导航方法进行深入研究。

