基于虚拟圆球法向量的极区惯性导航算法
刘 潺,吴文启,冯国虎,王茂松
(国防科技大学 智能科学学院,长沙 410073)
随着极区航线的开发,近年来极区导航已经成为了一个研究热点问题。由于惯性导航拥有极好的自主性,并且不受极区地磁变化和太阳风暴的影响,因此惯性导航已经成为极区重要的导航手段。极区子午线密集汇聚引起经度退化,极点附近纬度的正切正割计算奇异,使得传统的当地水平地理坐标系下的惯性导航解算误差急剧增大。
目前极区惯性导航的主流解决方案有格网坐标系和横坐标系导航算法。这两种算法在圆球模型下会不可避免地产生原理性误差,而采用椭球模型进行导航解算则会使计算过程变得复杂[1,2]。文献[3]提出了虚拟圆球的概念,利用虚拟圆球模型简化极区导航力学编排,其精度与椭球模型一致。
格网坐标系导航算法在赤道附近无法正常工作,横坐标系算法会在赤道产生新的极点,因此二者都不具备全球导航能力。另外,格网坐标系与横坐标系导航算法不能用统一的全球误差模型分析其误差特性,特别在穿越极区的应用场景中,都需要与传统的地理坐标系导航算法进行切换,这样会带来积分过程的变化,对于阻尼算法和组合导航滤波算法,切换过程会影响内部算法的连续性与一致性,同时还极大地增加算法复杂度。间接混合导航算法[4,5]通过对不同坐标系导航算法输出参数的结合实现全球导航,但是一致性问题仍然没有完全解决,算法复杂度偏高。
文献[6]强调要解决全球适用的问题,需要选择一个完全独立于地球形状和系统位置的导航坐标系,例如地球坐标系。文献[7]提出了一种非奇异的法向量(n-vector)水平位置表示方法。文献[8]根据法向量方法实现了具有全球适用性的力学编排方案,但是该方法在法向量更新算法中仍需要引入北向和东向速度,导航结果转换到其他坐标系比较复杂。
在此基础上,本文提出了虚拟圆球模型下的法向量四元组位置表示方法,研究一种形式更简洁、实现更简便的适用于全球的惯性导航力学编排方案,分别从垂直通道和水平通道分析其误差特性并基于实际航海导航数据进行了仿真验证。
1 基本定义与基本原理
1.1 横地理坐标系力学编排的局限
当载体处于极区时,通常采用横经度λt和横纬度tL表征水平位置,用横坐标系进行导航解算。如图1所示,横地球坐标系的xte轴与原地球坐标系的ze轴重合,yte轴与xe轴重合,zte轴与ye轴重合。因此地球坐标系e与横地球坐标系et的方向余弦表示为:

横地理坐标系(nt系)北向与当地水平地理坐标系(n系,东北天)北向与之间的夹角为β,则由定义可得方向余弦矩阵表示为[1]:
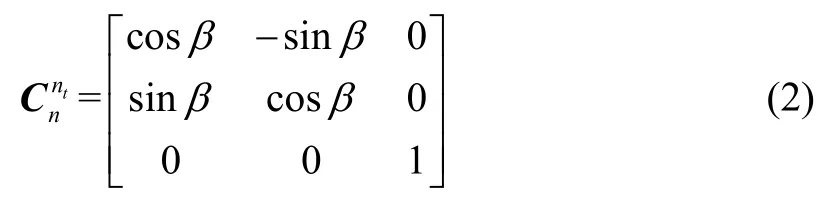
其中


图1 横坐标系示意图Fig.1 Sketch of transversal frame
横地理坐标系相对于地球系的转动角速度在横地理坐标系下的投影,如果采用圆球模型进行导航解算会存在原理性误差,而采用参考椭球模型时表示为[1]:
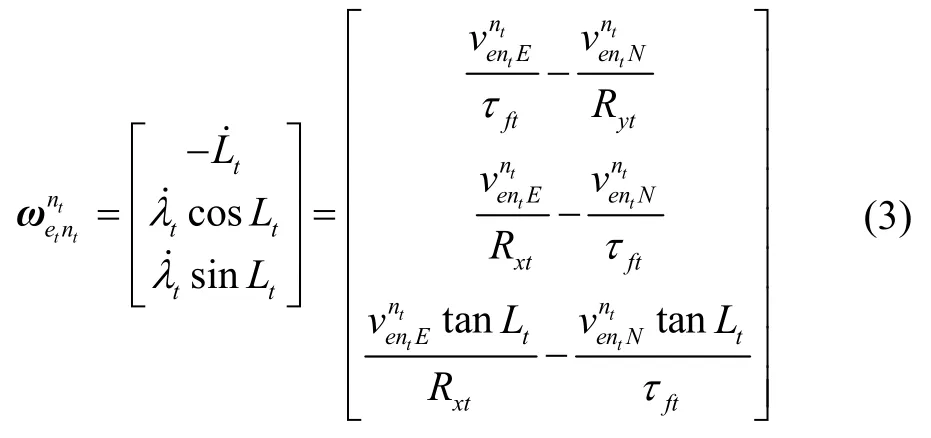
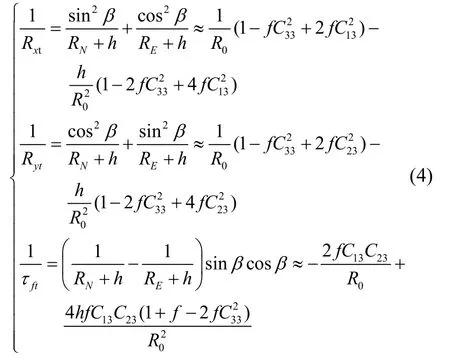
因此采用横坐标系进行导航解算会遇到一些问题:一是涉及多个方向的曲率半径,计算过程比较复杂;二是近极点处的sinβ、cosβ以及曲率半径由于经线汇聚无法精确得到,极区姿态解算、速度解算存在误差,当惯导系统本身已经存在位置误差时,由此造成的误差就会更加显著。
1.2 格网坐标系力学编排的局限
格网坐标系Gn如图2所示,σ为格网坐标系Gn北向与地理系n北向之间的夹角,记顺时针方向为正。由定义可得方向余弦矩阵表示为:

其中

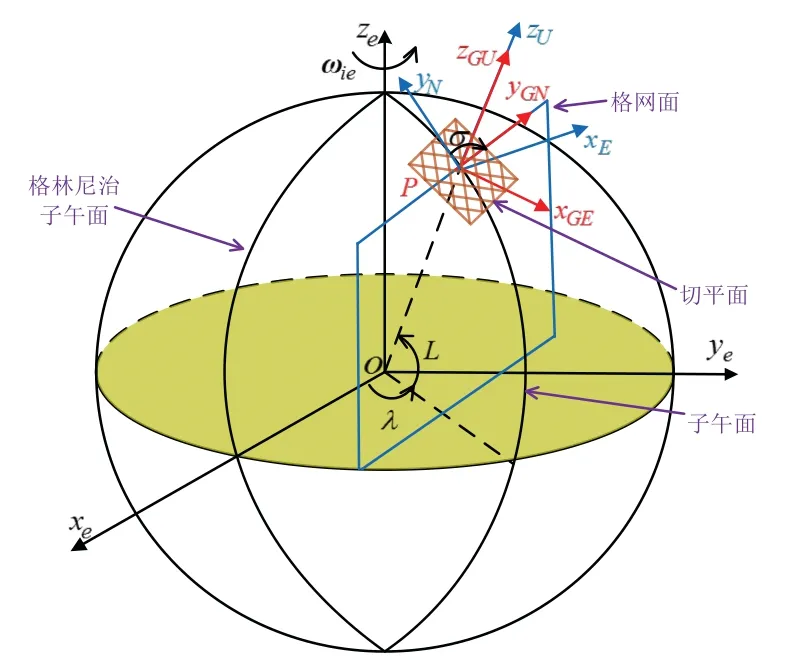
图2 格网坐标系示意图Fig.2 Sketch of grid frame
格网坐标系相对于地球系的转动角速度在格网坐标系下的投影表示为[2]:


对比两种坐标系下的计算过程,算法结构本质上是一致的,具有相同的天向坐标轴,只是格网北向与横地理坐标系北向的定义不同。因此,格网坐标系下的计算存在和横坐标系相同的问题。
1.3 虚拟圆球法向量模型
目前传统的位置表示方法是使用经纬度(横经度横纬度)高程表征位置。然而由于所有经线在极点处交汇,因此极点处的经度没有定义,经纬度位置表示方法存在奇异性,而当载体接近极点时,这种表示方法会导致极区导航算法的精度降低。此外,当载体位于180 °经线时,经度表示位置不连续,会影响计算的连续性。同理,横经度横纬度的表示方法会在赤道上产生新的极点,同样不适用于全球导航算法。虽然地心直角系的位置表示方法具备全球适用性,但这种方法不能直接表示载体相对地球参考椭球表面的高度、横向位置及其变化,得到的导航结果在需要进行坐标系转化时比较复杂。
为了解决传统位置表示方法的奇异性问题,本文在虚拟圆球模型的基础上,提出用四维向量表示三维位置的方法,如图3所示。
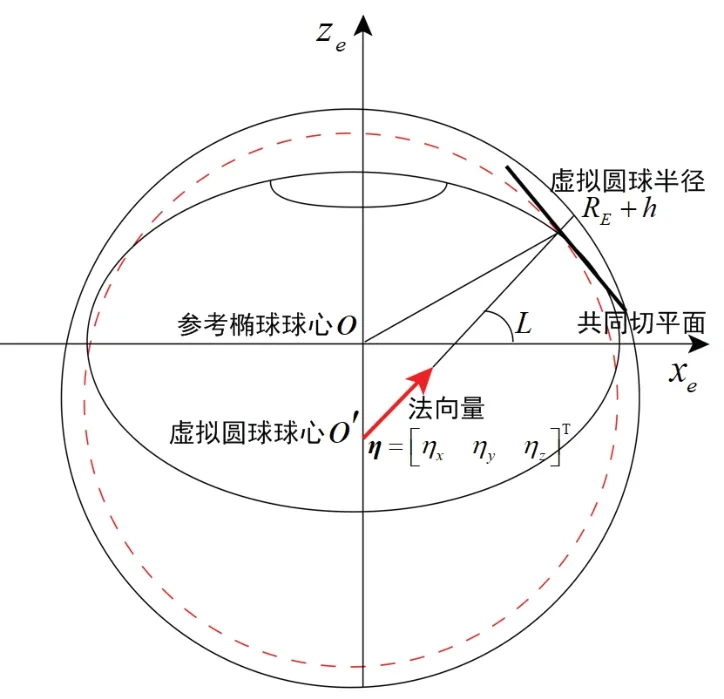
图3 虚拟圆球法向量示意图Fig.3 Sketch of virtual sphere N-vector
由载体对应参考椭球位置的卯酉圈构造一个虚拟圆球,其球心为对应卯酉圈的圆心,圆球半径为卯酉圈半径ER与大地高度h之和。
在新的虚拟圆球模型下,用包含法向量的四元组Pη=[ηxη yηzh]T表示载体位置。法向量η= [η xη yηz]T是虚拟圆球球心指向载体位置的单位矢量,实质上也就是当地水平面法向量在地球坐标系下的投影,用来表征载体的水平位置。大地高度h即载体位置相对地球椭球模型表面的高程,表征载体的垂直位置。由法向量定义可得:
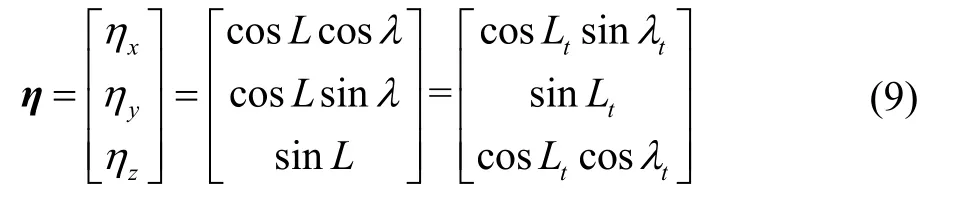
四元组Pη与地球坐标系下载体到地心的位置矢量的转换关系可以表示为:
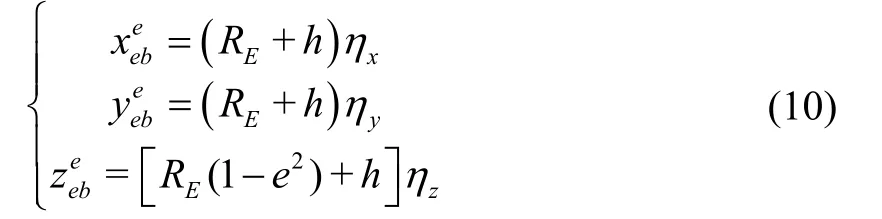
采用地理坐标系n进行导航解算,将式(6)代入方向余弦矩阵可得:

由式(2)(8)可以推导出e系与nt系的方向余弦矩阵得:

由式(4)(8)可以推导出e系与nG系的方向余弦矩阵得:

由于虚拟圆球法向量模型在地球坐标系下的惯性导航力学编排只需要涉及参考椭球模型中的精确的子午圈和卯酉圈半径计算,避免了复杂的沿其他方向的曲率和扭曲率半径计算,避开了计算横地理坐标系和格网坐标系相对地球的转动角速度的复杂过程,有利于提高极区导航位置、速度姿态微分方程的解算精度。此外,虚拟圆球法向量的位置表示方法还能够方便地得到地球坐标系与横向、格网导航坐标系的方向余弦矩阵,便捷地将导航参数转换为各种坐标系下的导航参数。
2 基于虚拟圆球法向量的力学编排
2.1 位置微分方程
基于虚拟圆球法向量的导航力学编排方案选取地球坐标系为导航坐标系,用四元组代替经纬高进行位置更新。
在垂直方向上,由于虚拟圆球法向量与载体垂直高度方向一致,因此载体垂直方向上的微分方程为:

在水平方向上,根据式(6)(7)可以推导出虚拟圆球法向量η的微分方程用子午圈半径RN、卯酉圈半径RE与大地高度h表示为:

即位置微分方程整理可得:

式中KR为参考椭球变换为虚拟圆球的尺度系数矩阵,kR为尺度变换系数,与文献[3]一致,即:

观察位置微分方程的物理意义可得,虚拟圆球的球心为对应卯酉圈的圆心,半径为RE +h。
2.2 速度微分方程
地球坐标系下的速度微分方程为:

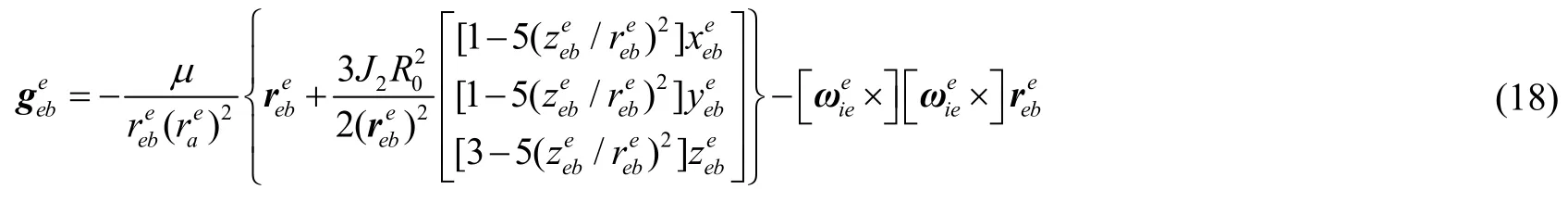
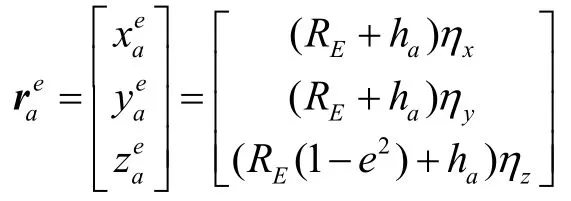
2.3 姿态微分方程
地球坐标系下的姿态微分方程为:

综上,基于虚拟圆球法向量的惯性导航力学编排如图4。
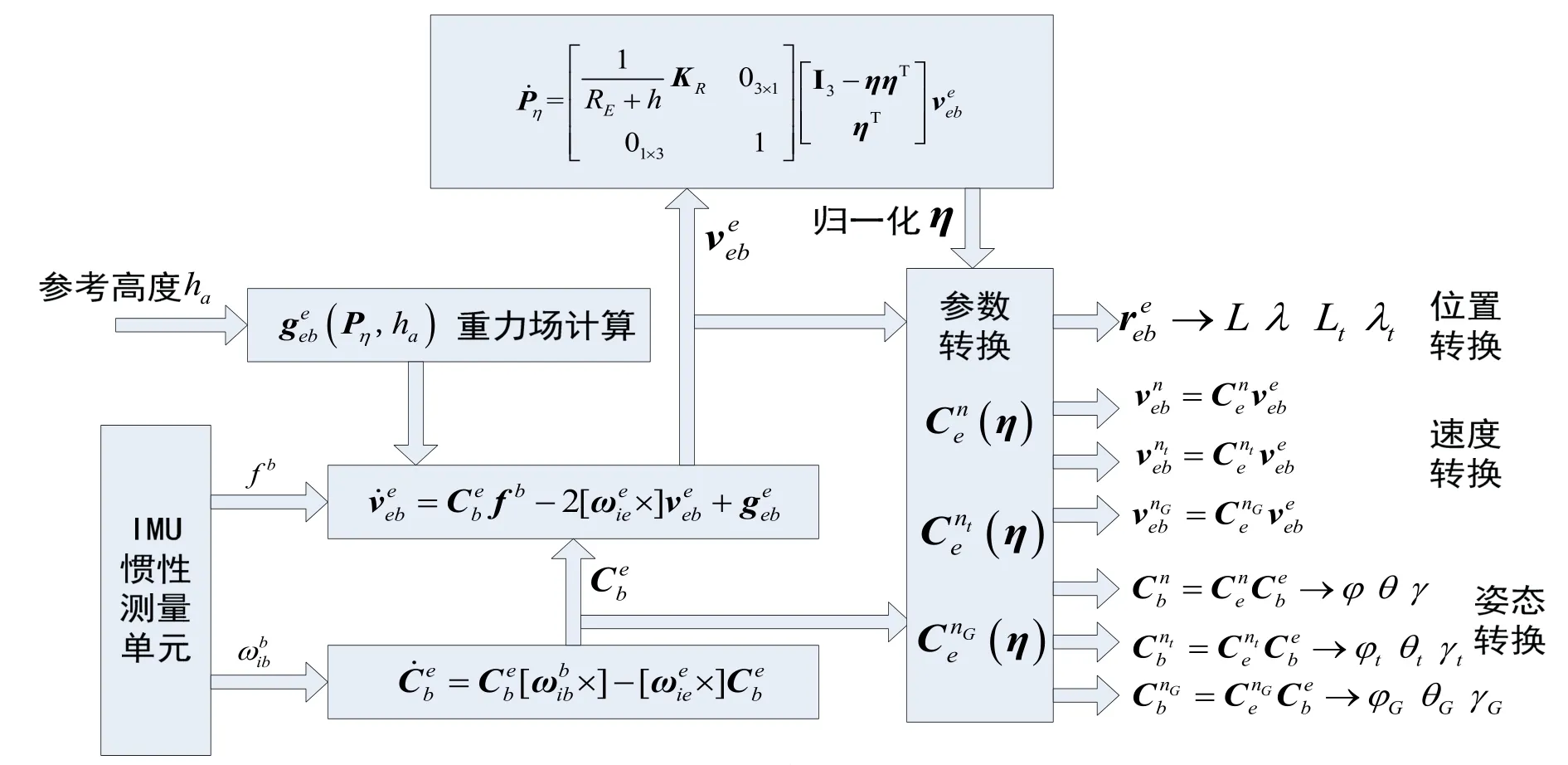
图4 力学编排框图Fig.4 Diagram of mechanization
综上,基于虚拟圆球法向量的极区惯性导航力学编排的姿态微分方程、速度微分方程与地球坐标系下的解算方程形式基本一致,而位置微分方程则是四元组Pη的方程。由于η是当地水平面法线方向单位矢量在地球坐标系下的投影,无论在极区或非极区都不会出现退化问题,使新的力学编排具备了全球适用性。上述力学编排不需要涉及多个方向的曲率半径的计算,而且在各个坐标系下的导航参数转换方便,在保证精度的同时,复杂度相对较低。
3 基于虚拟圆球法向量的算法误差特性分析
为了分析新模型下的导航性能,同时为以后的阻尼工作做准备,推导其误差方程如下。
vh为当地垂直方向的速度,即
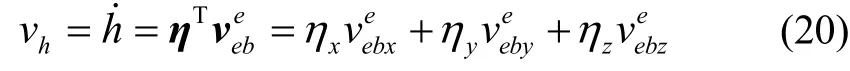
为水平方向速度在地球坐标系中的投影,即

由速度微分方程式(14)(17)(18)可得:
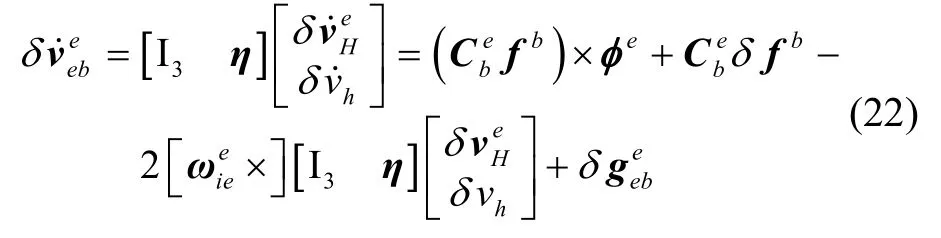
3.1 垂直方向误差微分方程
观察静基座的高度通道,用ωs表示舒勒周期角频率,由近似算法可得:

由式(17)(19)(20)可以得到:

3.2 水平方向误差微分方程
同理,在静基座的水平通道上,忽略小项后整理得速度误差微分方程为:
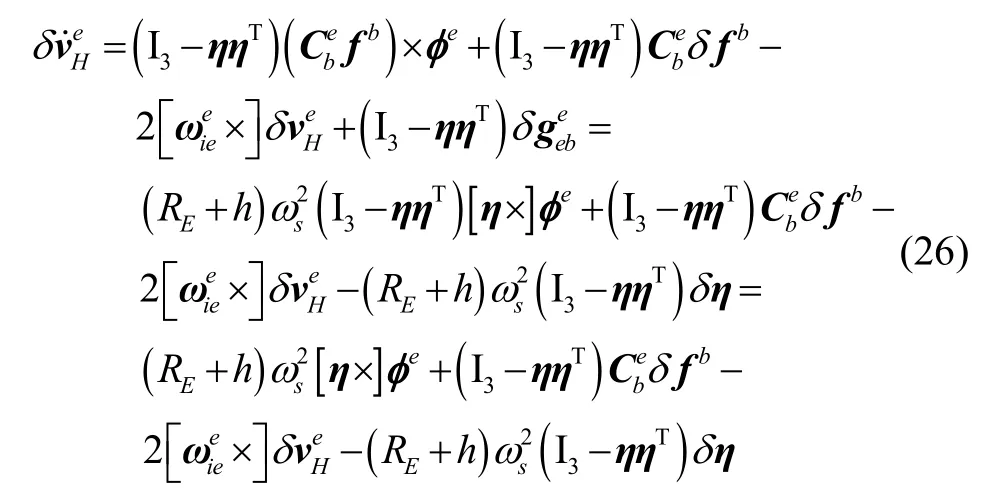
另外,姿态误差微分方程为:
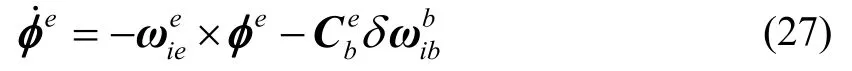
水平位置误差微分方程为:
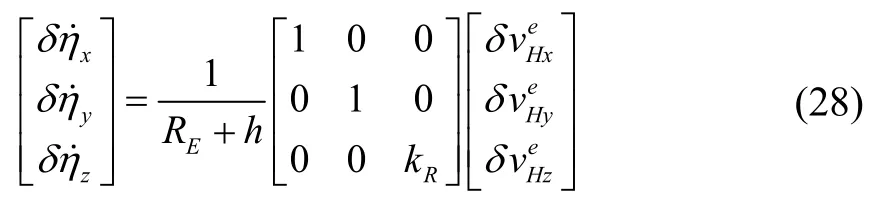
整理式(26)(27)(28)得到水平通道的误差微分方程式:
因此由式(20)(24)可以得到静基座下高度通道的速度、位置误差微分方程:

因此,可以得到状态转移矩阵的特征方程:


在配方过程中忽略和项,可以得到
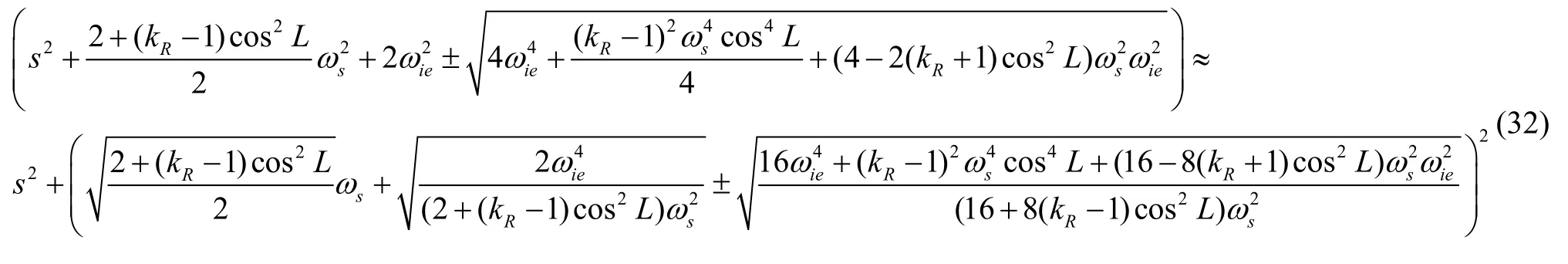
观察特征方程根的情况,除3 个零根外,有一对虚数根 ±jω ie,即地球周期振荡对应的角频率。另外由得到的两对虚数根可以得到角频率ω1与角频率ω2。
角频率ω1为:
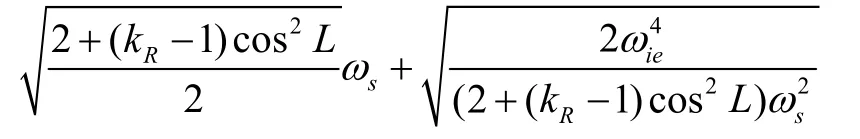
角频率ω2为:

由定义可得kR的取值范围为[0.9933,1],而,因此ω1≈ωs,也就是舒勒周期对应的角频率;ω2≈ωiesinL,也就是傅科周期对应的角频率,特别是当靠近极点时,傅科周期退化为地球周期。
4 仿真实验
4.1 三种算法的静态仿真实验
考虑到极区导航实验的特殊性,文献[9]提出了一种“极区高度仿真”的数据转换方法,将低纬度实际航行的导航数据转换成高纬度仿真数据。为了与文献[1]的横坐标系算法、文献[2]的格网坐标系算法做对比,采用这种转换方法将80 h 静态数据(200 Hz)转换至北纬85°做极区静态纯惯导仿真,纵坐标用归一化误差表示,横向位置误差如图5所示。
由图5可以看出,格网坐标系与横坐标系的导航解算结果重合,本文所提出的新方法的精度略有提高,同时避免了出入极区时的切换操作。另一方面,由于新模型不需要计算格网坐标系或横坐标系在椭球模型下的多个方向的曲率半径,因此计算耗时较少。如表1所示,以格网系的算法耗时为标准,横坐标系的算法耗时与格网系相当,而新算法的耗时大约节省了20%。
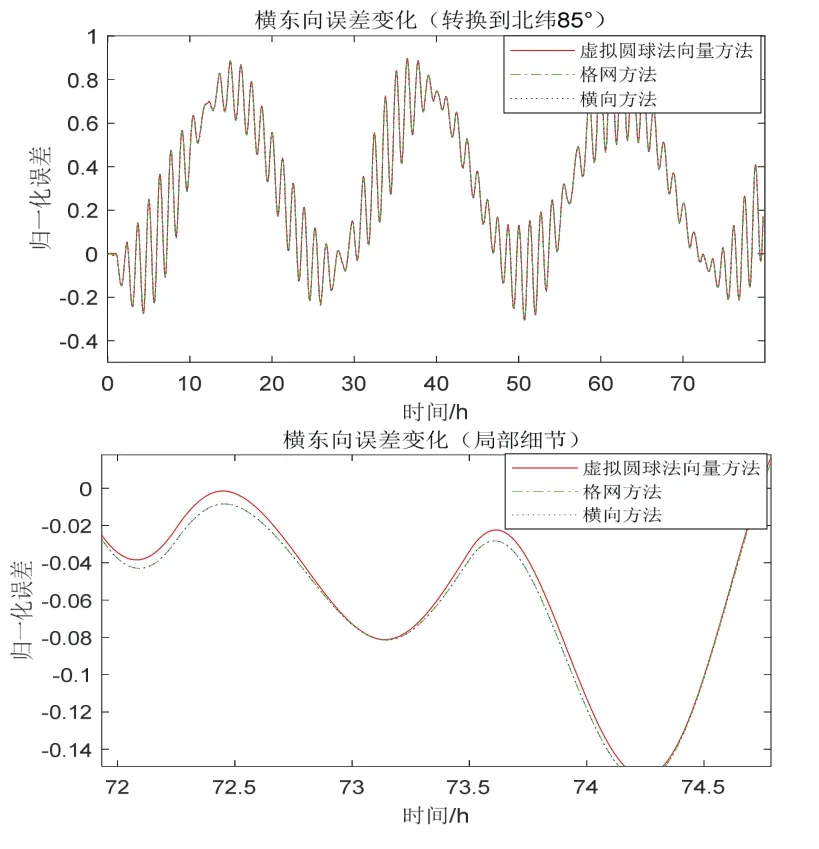

图5 横向位置误差Fig.5 Transversal position error

表1 三种方法的耗时Tab.1 Time spent on three algorithms

表2 多次仿真的结果对比Tab.2 Results of multiple simulations
为了验证算法的有效性,分别将初始位置转换到极区多个地方进行了仿真验证,多次仿真结果如表2所示。实验结果表明,转换到极点时,新算法和格网坐标系、横坐标系的解算结果重合,而转换到北纬85°时,归一化误差大约减小了0.0025。根据式(3)(5),在极点处传统极区导航算法没有曲率半径的近似计算误差,而随着位置偏离极点,近似误差逐渐增大,与实验结果相一致。
4.2 三种算法的动态半实物仿真实验
将起始位置(28.22° N,112.99° E)的15000 s 实际航行数据转换至极区(85° N,0° E)即横经度5° 横纬度0°进行动态仿真实验,基于虚拟圆球法向量的算法与极区传统导航算法的轨迹与横向位置误差如图6所示。
由图6可以看出,本文所提出的新方法与格网坐标系、横坐标系导航算法的轨迹基本重合,精度略优于格网坐标系、横坐标系下的算法。图中误差曲线可以看到一些突起,这是由于参考真值(GPS)的跳变所导致的。
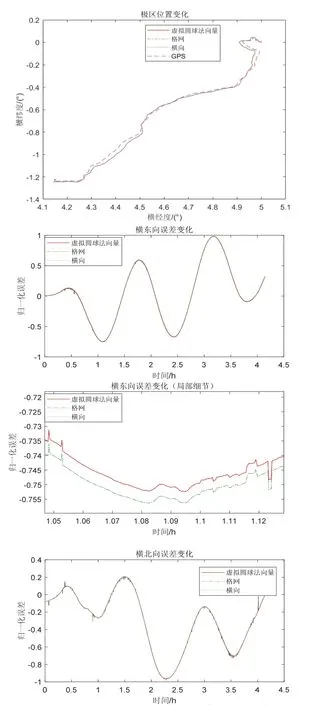
图6 极区的航迹与横向位置误差Fig.6 Track and transversal position error in polar region
综上,基于虚拟圆球法向量的极区惯性导航算法适用于穿越极区的场景,具有全球适用性。算法的性能与格网坐标系或横坐标下的算法相比,实现方便,耗时较少,精度略优。
5 结 论
为了解决全球适用性问题,本文提出了虚拟圆球法向量的四元组载体位置表示方法。在此基础上,实现了精度较高复杂度较低适用于全球的惯性导航力学编排方案,分析了误差特性,为下一步的阻尼工作打下了基础。通过静态与动态半实物仿真实验,新算法与传统极区算法相比,形式简洁容易实现,避免了出入极区的复杂切换,具有全球适用性。

