多支撑区域模式化融合角点检测算法仿真
宋智礼,张家齐
(上海应用技术大学,上海 201418)
1 引言
近年来人工智能技术高速发展,计算机视觉相关技术成为研究者们关注的焦点。经过多年的研究,在对图像的处理中,特征检测的重要地位逐渐建立起来。在图像的众多特征中,特征点因其具有旋转不变性、尺度不变性等优点而备受研究者的青睐。目前对于特征点并没有严格的定义,相对公认的理解[1]是从广义和狭义两个方面定义的。广义上来讲,特征点是图像中某种特性的位置,不需要满足物理上对特征的定义。狭义上来讲,特征点代表一种常规特征属性,反映该点相对于其小范围邻域内的其它点的特殊性。本文算法检测的角点属于狭义特征点范畴。
到目前为止,角点检测根据检测机理不同,可大致分为两类,分别是基于灰度的角点检测算法[2]和基于轮廓的角点检测算法[3-4]。本文角点检测算法是基于图像轮廓的。基于图像轮廓的角点检测算法通常是利用轮廓曲线上某点的几何位置信息或者曲率来衡量曲线上该点所在位置的弯曲程度,以此判断该点是否为较角点。早期此类算法中较为经典的是Mokhtarian等人于1988年提出的CSS(Curvature Scale Space)算法[5],该算法利用轮廓曲线上每个像素点的曲率值来衡量角点响应程度。该算法的突出贡献在于它引入了曲率尺度空间的定义,实现了在不同尺度下检测和定位角点。后来的研究者在此基础上提出了一系列改进算法[6-7]。2008年,Awrangjeb等人提出CPDA(Chord-to-Point Distance Accumulation)算法[8],该算法利用轮廓曲线上点到弦距离的累加和来计算角点响应值。随后学者在此基础上进行了改进和应用[9-11]。Rosenfeld等人提出了k-余弦曲率算法[12],用轮廓曲线上点与其邻域内的点所成夹角的余弦值作为该点曲率的度量,以此来判断该点是否为角点。
本文算法在k-余弦曲率算法为基础,创新性的提出了多支撑区域模式化融合的角点检测算法,在一定程度上解决了以往基于图像轮廓的角点检测算法中阈值选择的困难,有效的提高了角点检测的精度。
2 k-余弦曲率算法
2.1 曲线的描述
提取图像轮廓后,得到闭合轮廓曲线,为曲线像素点的集合,即
L={pi=(xi,yi)|i=0,1,…,N-1}
(1)
其中,N为组成轮廓曲线的像素点的个数,pi和pi+1是曲线上相邻的两个像素点。
2.2 支撑区域的定义
记曲线L上任意一点pi为点A,Pi-k为点B,Pi+k为点C。
(2)
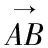
(3)
在计算cik时,需要在一个区域n内选择一个合适的k值,这里的n(n≥k)被定义为支撑区域。
2.3 k-余弦曲率算法的描述
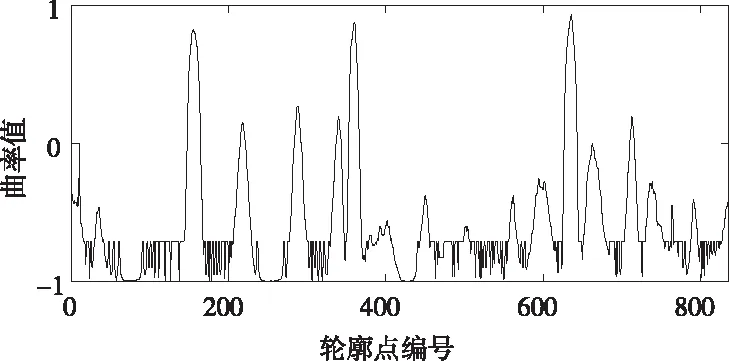
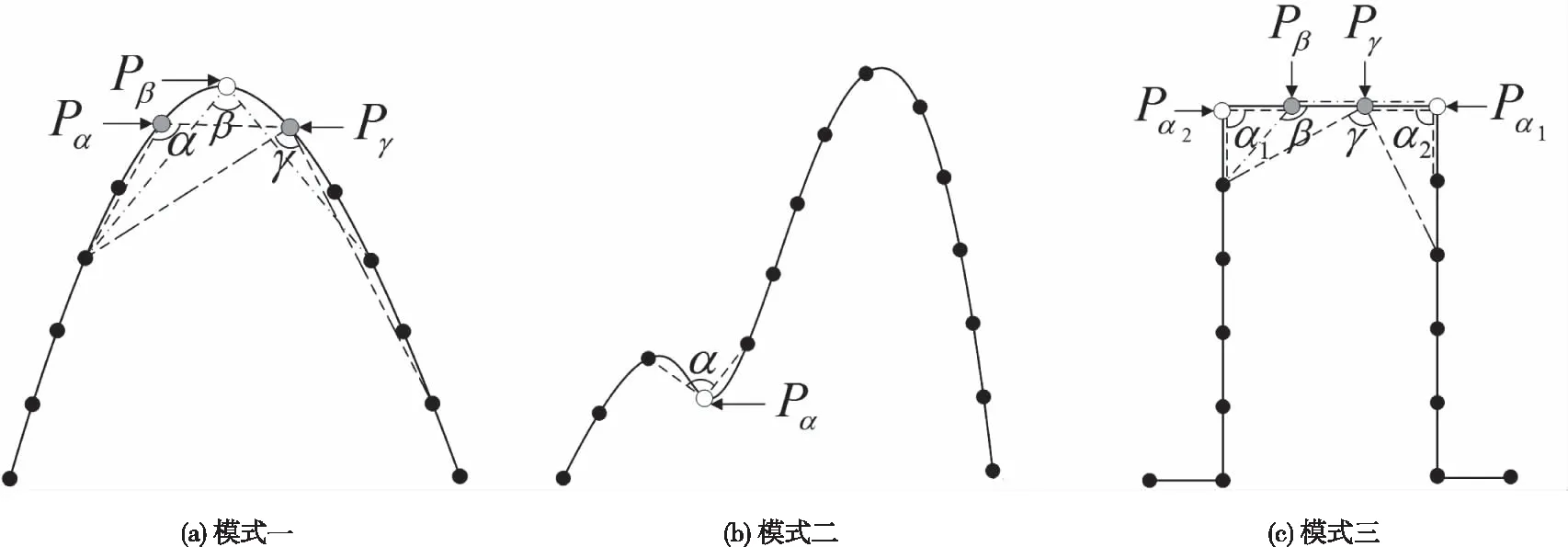
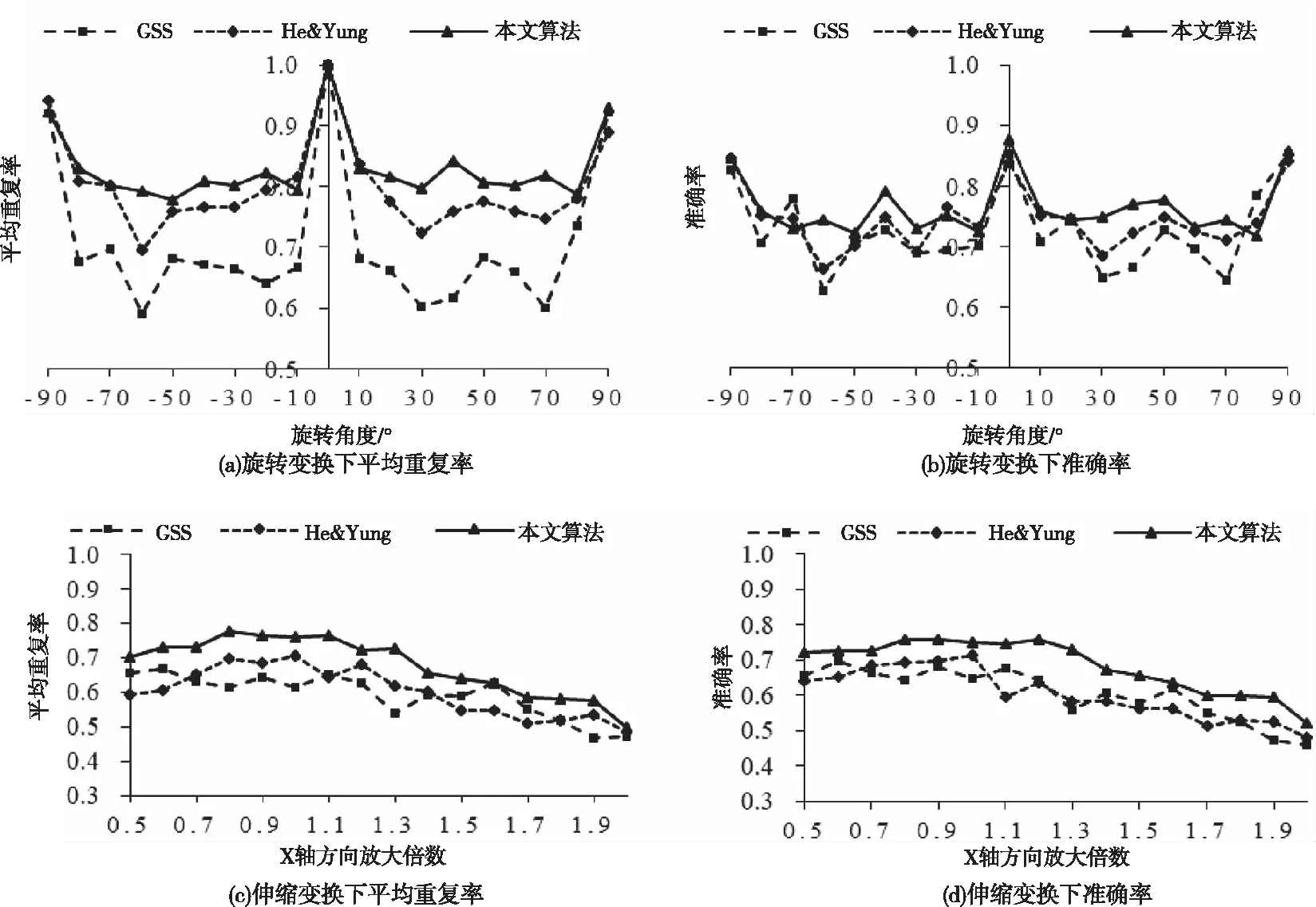
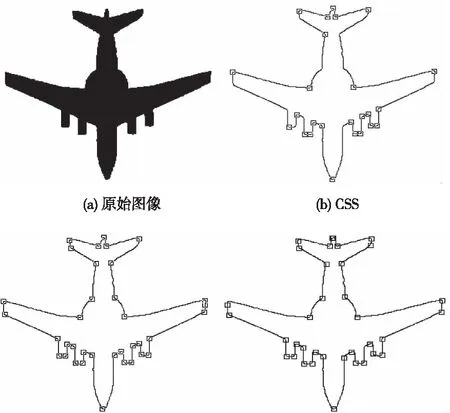
1)任取支撑区域n 2)对曲线L上的每一个点pi计算cik,k=1,2,3,…,n。 3)选取最大余弦值cih来代表pi处曲率的大小,记为ci,即cih≥cik,1≤k≤n且k≠n。 4)对于满足|i-j|≤h/2的所有j,如果有ci≥cj,则pi为曲线L上的一个角点。 在重复的试验中可以发现,支撑区域取值越小,越容易检测到轮廓曲线上局部的微小变化(如图1上的点P),而难以检测到轮廓曲线上的较大的弯曲(如图1上的点Q)。反之,支撑区域取值越大,越难以检测到曲线上的微小变化。显然,想要准确得出曲线上的所有角点,对于曲线上各个局部就需要选取不同的支撑区域。本文在传统的k-余弦曲率算法的基础上进行了改进,使用多个不同的支撑区域计算曲率,减小了曲率选择不当带来的误差,提高了角点检测的准确率。 图1 轮廓曲线上不同局部的弯曲程度不同 本文算法的具体步骤如下: 1)提取图像轮廓曲线; 2)先任选一个支撑区域,按照k-余弦曲率算法对曲线上每一个点计算ci,i=0,1,…,N-1;某条轮廓曲线上各店曲率值如图2所示。 图2 轮廓曲线上各点曲率值图 3)选择一个较为宽松的阈值T对曲线上的点进行初步筛选,保留ci>T的点,经过筛选后保留下的点称为初选角点; 4)对初选角点进行分组; 5)在每组中选取一个或多个点作为备选角点; 6)选取不同的支撑区域,重复步骤2)-4); 7)将多个备选角点集进行模式化融合,删除重复、多余的角点。 3.2.1 分组的方法 经过3.1节的步骤3的初步筛选,能够大致确定曲线上角点的位置,此时保留下来的点数量较多,需要进一步筛选。可以发现,初选角点集中分布在真实角点的附近。将曲线上位置相近的点划分为一组。具体方法如下: 1)将第一个初选角点的分组编号设为1; 2)从第二个初选角点开始,依次判断是否与上一个初选角点相邻(本文算法中设定在曲线上相距3个像素以内即判断为相邻),如果相邻,则与上一个初选角点划分为同一组;如果不相邻,该点为下一个分组的起始点,直到遍历所有初选角点。分组结果如图3所示。 图3 分组结果示意图 3.2.2 备选角点的选取 备选角点的选取在每组点中独立进行,每一组点中选出一个或多个备选角点。在某组中,对于满足|i-j|≤r/4的所有j,如果有ci≥cj,则pi为一个备选角点,其中,r代表该组中点的个数。 3.2.3 支撑区域的选取 本文2.4节部分描述了支撑区域的选取和曲率计算结果的关系。本文算法中需选取m个大小不同的支撑区域。最小的支撑区域决定了算法可检测到的曲线上最小的弯曲程度,本文取为5。考虑到如果支撑区域取值太大,会对程序执行时间产生较大影响,本文算法最大的支撑区域取为min{N/20,20}(N表示构成轮廓曲线的点的个数)。其余支撑区域选取从最小值开始依次乘以2。本文实验中选取m=3,故支撑区域依次为5,10,20。 3.2.4 轮廓曲线模式划分及角点融合方法 根据不同的支撑区域会选取多个备选角点集,需要将这些点集进行有效的融合,保留正确的角点,删除重复和错误的角点。本文算法将曲线上的复杂变化概括为以下三种模式,在不同的模式下使用相应的方式进行角点的融合,以m=3(即选取3个不同支撑区域)的情况进行说明,三个支撑区域由小到大分别为α,β,γ,在每种模式中检测出的角点分别为Pα,Pβ,Pγ,示意图中正确检测到的角点用白色点表示,重复或错误的角点用灰色点表示。 模式一:曲线上较大的弯曲处,如图4(a)所示,这种情况下,选取最小的支撑区域时,难以准确检测到角点,选取其它较大的支撑区域时都可以较为准确的检测到角点。此时在真实角点附近会出现m个或m个以下备选角点,只需要任选一点或选取曲率最大值点作为角点,删除其它备选角点即可。 图4 轮廓曲线模式图 模式二:曲线上微小波动处,如图4(b),这种情况下,只有在选取最小的支撑区域时可以检测到角点的存在,此时在真实角点附近只有1个备选角点,保留即可。 模式三:曲线上的方形突起处,如图4(c),这种情况下,当选取较小的支撑区域时,可以准确的检测到每一个角点,如图4(c)中的Pα1点和Pα2点,当选取较大的支撑区域时,只能检测两个真实角点之间的某一个点,如图4(c)中的Pβ点和Pγ点。此时,在真实角点附近会出现大于或等于m个备选角点,保留两边的备选角点,删除其它的备选角点即可。 为验证本文算法的有效性和准确性,在PC机(Inter(R)Core(TM)i5-5200 CPU @ 2.20GHz,4G内存)上进行实验,所用软件为Visual Studio 2017。分别对He&Yung,CSS以及本文算法进行性能评估。 实验所用原始图像来自文献[13]。每幅原始图像经过旋转变换和伸缩产生多幅测试图像。旋转变换从-90°到90°,每隔10°旋转一次,每幅原始图像会产生18幅旋转变换图。伸缩变换中,x方向放大倍数从0.5到2,相应地,y方向放大倍数从1.8到0.3,每幅原始图像会产生16幅伸缩变换图。 实验采用了两种性能评价指标,分别为平均重复率(average repeatability)[14]和准确率(accuracy)[15]。用R代表平均重复率,A代表准确率,Nr是指在原始图像和变换图像中都被检测到并且匹配的角点数目,No是指在原始图像中被检测到的角点数目,Nt是指在变换图像中被检测到的角点数目,Na是指变换图像中被检测出的正确角点数目,Ng是指在原始图像中标注的正确角点数目。 Ro为Nr和No的比值,Rt为Nr和Nt的比值,Ro和Rt都可以表示重复率,但是问题在于这两种方法都对检测到的错误角点个数高度敏感。在极端情况下,如果角点检测器认为原始图像中所有的点都是角点,此时Nr=Nt,Rt=100%;如果角点检测器认为变换图像中所有的点都是角点,此时No=Nt,Ro=100%。为了降低错误角点个数对性能评估的影响,本实验采用Ro和Rt的平均值作为重复率的评价指标,称作平均重复率,其定义如下: (4) At为Na和Nt的比值,Ag为Na和Ng的比值。如果角点检测器检测到的角点个数很多,这意味着错误角点个数也会增加,此时At接近于0,而Ag接近于100%;如果角点检测器检测到的角点个数很少,那么正确的角点个数也会减少,此时At接近于100%,而Ag接近于0。为了更加准确的评估角点检测器是否能够尽可能多的检测到正确的角点,同时避免检测到错误的角点,本实验采用At和Ag的平均值作为准确率的评价指标,其定义如下: (5) 本文算法与其它两种算法比较结果如图5所示,图5(a),图5(b)显示了三种算法在旋转变换下的平均重复率和准确率,图5(c),图5(d)显示了在伸缩变换下的平均重复率和准确率。观察发现,旋转变换下,本文算法的平均重复率表现最佳,He&Yung次之,准确率三种算法相差不大,本文算法总体表现略高于其它两种算法。在伸缩变换下,本文算法的平均重复率和准确率都有较好的表现。这是由于本文算法采用了多支撑区域的方式,可以检测到轮廓曲线上不同弯曲程度下的角点,又在角点融合过程中删除了不正确的角点。 图5 实验结果图 图6展示的是三种算法检测结果的直观对比,此图像轮廓细节丰富,不同局部弯曲程度差异较大,角点检测难度较高,可以直观的体现算法角点检测性能强弱。可以看出,就此图像而言,CSS算法对于飞机机翼前侧细节检测效果较好,而对飞机机身以及飞机尾部几处明显的角点并没有检测到。He&Yung算法和本文算法能够较好的兼顾图像轮廓上不同局部的检测效果,而本文算法有更少的误检测点。综上所述,本文算法检测效果最佳。 图6 检测结果直观对比图 本文提出了一种多支撑区域模式化融合的角点检测算法,通过选取不同阈值计算出多组备选角点,以选取不同弯曲程度下的角点,提取曲线上跟多的有效信息,再对其进行模式化融合,删除多余重复的角点。该方法在一定程度上解决了阈值选择的问题,提高了对复杂曲线角点检测的能力。从实验结果可以看出,有效提高了角点检测的准确性,但在应对噪声以及效率方面有略有不足,下一步可以考虑针对此缺陷进行优化。本算法可应用于图像配准、形状分析、目标检测等领域。2.4 k-余弦曲率算法的的不足与改进

3 新算法实现
3.1 算法基本思路
3.2 算法的具体描述

4 实验结果分析
5 结论

