椭圆余弦波的位移法分析

吴锋 孙雁 姚征 钟万勰

摘要：

为研究线性浅水波理论的适用范围，基于位移浅水波方程的椭圆余弦波解，计算在不同水深h、波高η0和波长L条件下，非线性椭圆余弦波与线性余弦波的相对差。数值计算结果表明：η0/h越小或h/L越大，浅水波的非线性效应越弱；当η0≤0.42h且η0L2/h3≤5.34-12.85η0/h時，非线性椭圆余弦波与线性余弦波的相对差小于0.05，可满足工程需要。

关键词：

椭圆余弦波； 线性； 非线性； 浅水波理论； 位移法

中图分类号： O352； O353.2

文献标志码： A

Analysis on cnoidal wave using displacement method

WU Feng1， SUN Yan2， YAO Zheng3， ZHONG Wanxie1

（1. Department of Engineering Mechanics， Dalian University of Technology， Dalian 116023， Liaoning， China；

2. School of Naval Architecture， Ocean & Civil Engineering， Shanghai Jiaotong University， Shanghai 200240， China；

3. Transportation Equipment and Ocean Engineering College， Dalian Maritime University， Dalian 116026， Liaoning， China）

Abstract：

To study the scope of linear shallow water wave theory， the relative difference between nonlinear cnoidal wave and linear cnoidal wave is calculated by the cnoidal wave solutions of displacement shallow water equation in different water depth h， wave height η0 and wave length L. The numerical calculation results show that， the nonlinear effect of shallow water wave declines when η0/h decreases or h/L increases； the relative difference of nonlinear and linear cnoidal wave is less than 0.05 when η0≤0.42h and η0L2/h3≤5.34-12.85η0/h， which can satisfy the engineering requirement.

Key words：

cnoidal wave； linearity； nonlinearity； shallow water wave theory； displacement method

收稿日期： 2017-11-24

修回日期： 2017-12-08

基金项目：

国家自然科学基金（11472076，51609034，51278298）；中央高校基本科研业务费（DUT17RC（3）069）

作者简介：

吴锋（1985—），男，江苏靖江人，副教授，博士，研究方向为周期结构与计算动力学，（E-mail）vonwu@dlut.edu.cn

0 引 言

在波长为L的波浪由深海向近海传播的过程中，随着水深h逐渐变小，水平位移在垂向的梯度可忽略不计，此时可以用浅水波理论进行分析。浅水波理论包括线性和非线性2类。当使用线性浅水波理论时，需同时假定：（1） h远小于L；（2） 波高η0小于h。文献[1]第七章指出：对于许多实际海岸问题，假定（2）往往不能满足，需要研究非线性浅水波理论。与线性浅水波理论相比，非线性浅水波理论更加精确；然而，从数值计算的角度来看，非线性浅水波方程的求解比线性浅水波方程的求解复杂得多。本文对使用线性浅水波理论的ε=η0/h取值范围展开研究。

浅水波理论可分为基于Euler坐标和基于Lagrange坐标2类。法国学者

VENANT提出第一个非线性浅水波方程，采用Euler坐标。BOUSSINESQ[2]基于Euler坐标，首次提出同时考虑色散和非线性的浅水波方程。在此基础上，学者们通过摄动方法，提出种类繁多的BOUSSINESQ类方程[3-4]。2006年，钟万勰等[5-7]首先在Lagrange坐标下研究浅水波问题，提出包含竖向动能影响的位移浅水波方程，并给出位移孤立波解。位移浅水波方程的特点是保辛，可更好地体现浅水动力系统能量不变、体积不变等物理特性，其解的保真度更好。LIU等[8]在钟万勰等的研究基础上，将位移浅水波方程扩展到二维浅水波问题，并研究了二维位移浅水波方程的对称性[9]和解析解[10]。文献[11-15]研究位移浅水波方程的数值计算，并提出多种保辛计算格式。文献[16]研究二维位移浅水波方程并给出相应的二维位移孤立波解。文献[17]给出位移浅水波方程的椭圆余弦波解，该解可退化为孤立波解。

与BOUSSINESQ类浅水方程相比，位移浅水波方程的解保辛，可以更好地保持水波的能量、质量等物理量。本文基于位移浅水波方程的椭圆余弦波解，研究ε=η0/h对线性浅水波和非线性浅水波解的影响，进而研究线性浅水理论的适用范围。

1 位移椭圆余弦波

根据文献[5]和[6]，位移浅水波方程可以写为

-

h23

xx-ghuxx+3ghuxuxx=0

（1）

式中：g和u分别为重力加速度和水平位移；x为空间坐标。水面可以表示为

η=-hux

（2）

将式（1）中非线性项略去，得到线性位移浅水波方程为

-

h23

xx-ghuxx=0

（3）

式（3）中的第二项体现了垂直方向的动能影响，而普通线性解不考虑垂直方向的动能影响，不出现这一项。须构造式（1）的非线性椭圆余弦波和式（3）的线性余弦波，要求两者的波幅和波长均相同。

1.1 线性余弦波解

构造式（3）的特解，要求其水面为余弦波。若η=-hux是余弦波，则u是正弦波，可设

ul（ξl）=

u0sin（kx-ωt）=u0sin（kξl）

cl=ω/k

ξl=x-clt

（4）

式中：u0待定；ω为频率；k为波数；cl为波速；t为时间。将式（4）代入（3）可得线性浅水波的色散关系为

c2l=3ghk2h2+3

（5）

根据式（4）可知其水面高度为

ηl=-hux=-hu0kcos（kξl）

（6）

式（6）为线性余弦波。波高和波长分别为η0和L，有

2πk=L，-hu0k=η02（7）

水面高度可写为

ηl=

η02coskξl=η02-1+2cos2k2ξl

（8）

cl可写为

c2l=3ghk2h2+3=3ghL2（42h2）+3L2

（9）

1.2 非线性椭圆余弦波解

分析非线性位移浅水波方程的椭圆余弦波，要求其波高和波长分别为η0和L。椭圆余弦波是行波解，于是令

un=f（ξn），ξn=x-cnt

（10）

将式（10）代入式（1）可得

c2d2f2dξ2-c2h23d4f4dξ4-ghd2f2dξ2+3ghdfdξ d2f2dξ2=0（11）

根据文献[17]，式（11）的解可写为

f·（ξn）=λ2+（λ3-λ2）cn2（Κξn，m）

Κ2=3g（λ1-λ3）4hc2n

（12）

式中：cn为Jacobi椭圆余弦函数；m∈0，1为cn的模数，表示为

m2=λ2-λ3λ1-λ3

（13）

式（13）中λ1>λ2>λ3满足式（14）所示的3个恒等式。

-（λ1+λ2+λ3）=c2n-ghgh

λ1λ2+λ1λ3+λ2λ3=-2J1gh

λ1λ2λ3=2J2gh

（14）

式中：J1和J2为待定常数。结合式（2）、（10）和（12）可得水面高度表达式为

ηn（ξn）=-hf·=

-h（λ2+（λ3-λ2）cn2（Κξn，m））（15）

式（15）即为位移椭圆余弦波解。

椭圆余弦波为周期解，η0可定义为波峰与波谷之差。根据式（15），η0可表示为

η0=h（λ2-λ3）或λ2-λ3=ε

（16）

将式（16）代入式（13）可得

m=ελ1-λ3

（17）

联合式（14）和（16）可得

c2n=gh-gh（λ1+2λ3+ε）

J1=-gh2（（λ1+λ3）（λ3+ε）+λ1λ3）

J2=gh2λ1（λ3+ε）λ3

（18）

式（18）表明J1和J2可由λ1和λ3确定。根据Jacobi椭圆函数的性质可知，位移椭圆余弦波的波长为

L=2Κ（m）Κ， Κ（m）=∫π20dφ1-m2sin2φ（19）

式中：Κ（m）为第一类完全椭圆积分。仅依据式（19）无法确定λ1和λ3。考虑体积不变，即在一个波长内要求

∫L0ηn（ξn）dξn=0

（20）

将式（15）代入上式可得

-hλ2L+Lhε-hε2Κ

Κ（m）-E（m）m2=0

E（m）=∫π201-m2sin2φdφ

（21）

式中：E（m）为第二类完全椭圆积分。根据式（19）可知Κ=L-12Κ（m），代入式（21）可得

-λ2+ε-εΚ（m） Κ（m）-E（m）m2=0（22）

再將式（16）和（17）代入式（22）有

E（m）Κ（m）=λ1λ1-λ3

（23）

结合式（16）、（17）和（23）可得

λ1=E（m）Κ（m）

εm2

λ3=E（m）Κ（m）-1εm2

λ2=E（m）Κ（m）-1εm2+ε

（24）

将式（24）代入式（18）可得

c2n=gh-gh（λ1+λ3+λ2）=gh-

gh3E（m）Κ（m）εm2-2εm2+ε（25）

将式（25）和（24）代入式（12）可得

Κ2=3Κ（m）ε4h2（Κ（m）（m2+2ε-m2ε）-3E（m）ε）

（26）

再将式（26）代入式（19）可得

Lεh=43Κ（m）（m2+2ε-m2ε）-3E（m）εΚ（m）（27）

依据式（27）可以计算出m。将式（24）代入式（15）可得

ηn（ξn）

=h-εE（m）Κ（m）-11m2+1+

εcn2Κξn，m=

-η0E（m）Κ（m）-11m2+1+

η0cn2（Κξn，m）

（28）

从式（27）可见，m是无量纲参数，与h不直接相关，主要由参数Lε/h决定。该参数实际上是ε与h/L的比值，其平方即为Ursell参数U=L2η0/h3（见文献[1]的第七章）。如果Lε/h→∞，此时必有Κ（m）→∞，则m→1，那么解退化为孤立波解；如果Lε/h→0，有m→0，那么解退化为线性余弦波，此时

limm→0Κ=πL，

limm→0E（m）K（m）-11m2=-12（29）

所以其极限成为线性余弦波

limm→0ηn（ξn）=-η02+η0cosπLξn

（30）

2 数值比较

进行数值分析，比较非线性椭圆余弦波与线性余弦波之间的差异，进而研究线性浅水波理论的适用范围。定义椭圆余弦波与线性余弦波之间的相对差eη为

eη=ηl-ηn2ηn2=∫L0（ηl-ηn）2dξ∫L0（ηn）2dξ0.5（31）

式中：η2表示2范数。从式（8）和（28）可以看出，h和g的取值对eη没有影响，只有η0/h和h/L对eη有影响。在数值计算时，h和g为一组常数，即h=10 m，g=10 m2/s，而η0和L取不同值，以研究η0/h和h/L对eη的影响。

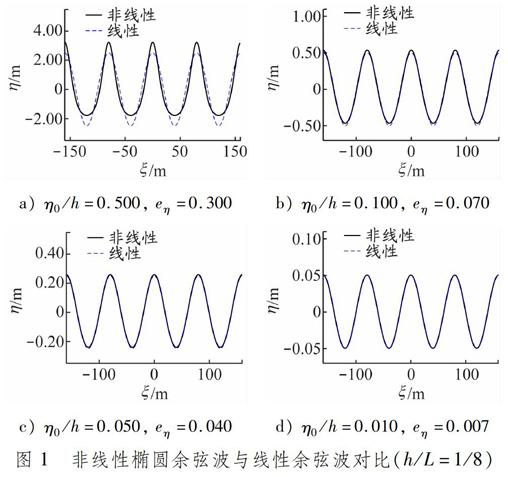
取h/L=1/8，η0/h=0.500、0.100、0.050和0.010进行计算，相应的U分别为32.00、6.40、3.20和0.64，计算得到的非线性椭圆余弦波与线性余弦波对比见图1。由此可知，随着η0/h的减小，U也逐渐减小，非线性椭圆余弦波逐渐退化为线性余弦波。当η0/h=0.050时，eη为0.040，已经小于工程要求的相对误差5%。

图 1 非线性椭圆余弦波与线性余弦波对比（h/L=1/8）

取h/L=1/20，η0/h=0.500、0.100、0.050和0.010进行分析，相应的U分别为200.00、40.00、20.00和4.00，计算得到的非线性椭圆余弦波与线性余弦波对比见图2。

图 2 非线性椭圆余弦波与线性余弦波对比（h/L=1/20）

图2表明，随着η0/h的减小，U逐渐减小，非线性椭圆余弦波逐渐退化为线性余弦波。当η0/h=0.010时，eη为0.040，已经小于工程要求的相对误差5%，即此时可以使用线性浅水波方程分析。比较图1和2可以发现，在相同η0/h的

条件下，随着h/L由1/8减小到1/20，U逐渐增大，浅水波的非线性程度亦增加。当η0/h=0.050时，h/L=1/8所对应的椭圆余弦波与线性余弦波的差异已经很小，而h/L=1/20所对应的eη为0.19，表明此时非线性效应还很强，线性理论还不适用。当h/L=1/20且η0/h=0.500时，U为200.00，此时的椭圆余弦波类似于一组孤立波。

为进一步研究h/L对非线性效应的影响，取h/L=1/30计算，此时η0/h取0.100、0.050、0.010和0.005，相应的U分别为90.00、45.00、9.00和4.50，计算得到的非线性椭圆余弦波与线性余弦波对比见图3。

图 3 非线性椭圆余弦波与线性余弦波对比（h/L=1/30）

从图3也可发现，随着η0/h的减小，U逐渐减小，非线性椭圆余弦波逐渐退化为线性余弦波。综合比较图 1～3可进一步说明，当η0/h不变时，随着h/L逐渐减小，U逐渐增大，非线性效应逐渐增加。当取h/L=1/30、η0/h=0.500时，计算得到的非线性椭圆余弦波与线性余弦波对比见图4，此时U为450.00，线性与非线性解的相对差达到1.06，非线性椭圆余弦波基本可视为由一组孤立波构成。

图 4 非线性椭圆余弦波与线性余弦波对比

（h/L=1/30，η0/h=0.500）

由图1～3可知：η0/h越小、h/L越大，非线性效应越小，即Lε/h越小，非线性效应越小。通过给定不同的η0/h和h/L，可以计算出eη的等值线，见图5。图中实线表示eη=0.050的等值线，每条eη的等值线都几乎为直线，所以η0L2/h3与η0/h基本是线性关系。采用线性关系拟合eη与η0/h以及η0L2/h3的关系，可以近似写为

eη=0.120 4η0h+0.009 4η0L2h3

（32）

图 5 eη的等值线

如果将eη=0.050視为线性浅水波理论适用的允许误差，在eη=0.050等值线左边是线性浅水波理论的适用区域，则该区域大致可描述为

η0h≤0.42， η0L2h3≤5.34-12.85η0h

（33）

即当η0≤0.42h，且U满足U≤5.34-12.85η0/h时，线性浅水波理论是适用的。

3 结 论

本文基于位移浅水波方程，通过数值比较非线性椭圆余弦波与线性余弦波的相对差，研究线性理论在浅水波分析时的适用范围。研究结果表明：

（1） η0/h和h/L对浅水波的非线性效应有重要影响。η0/h越小或h/L越大，浅水波的非线性效应越弱。当h/L不变时，随着η0/h的逐渐减少，非线性椭圆余弦波会逐渐退化为线性余弦波。

（2） 当η0≤0.42h且U≤5.34-12.85η0/h时，非线性椭圆余弦波与线性余弦波的相对差小于0.05，即线性浅水波理论满足工程需要。

参考文献：

[1] 梅强中. 水波动力学[M]. 北京： 科学出版社，1984.

[2] BOUSSINESQ J. Theory of wave and swells propagated in a long horizontal rectangular canal and imparting to the liquid contained in thiscanal[J]. Journal of Mathematics Pure and Applied. 1872， 17（2）： 55-108.

[3] 吴云岗， 陶明德. 水波动力学基础[M]. 上海： 复旦大学出版社， 2011.

[4] 邹志利. 水波理论及其应用[M]. 北京： 科学出版社， 2005.

[5] 钟万勰， 姚征. 位移法浅水孤立波[J]. 大连理工大学学报， 2006， 46（1）： 151-156. DOI： 10.3321/j.issn：1000-8608.2006.01.028.

[6] 钟万勰. 应用力学的辛数学方法[M]. 北京： 高等教育出版社， 2006.

[7] 钟万勰， 陈晓辉. 浅水波的位移法求解[J]. 水动力学研究与进展（A辑）， 2006， 21（4）： 486-493.

[8] LIU P， LOU S Y. A （2+1）-dimensional displacement shallow water wave system[J]. Chinese Physics Letters， 2008， 25（9）： 3311-3314.

[9] LIU P， LI Z L， LUO R Z. Modified （2+1）-dimensional displacement shallow water wave system： Symmetries and exact solutions[J]. Applied Mathematics and Computation， 2012， 219（4）： 2149-2157.

[10] LIU P， FU P K. Modified （2+1）-dimensional displacement shallow water wave system and its approximate similarity solutions[J]. Chinese Physics B， 2011， 20（9）： 90203. DOI： 10.1088/1674-1056/20/9/090203.

[11] 吴锋. 基于位移的水波数值模拟——辛方法[M]. 大连： 大连理工大学出版社， 2017.

[12] 吴锋， 钟万勰. 不平水底浅水波问题的位移法[J]. 水动力学研究与进展（A辑）， 2016， 31（5）： 549-555. DOI： 10.16076/j.cnki.cjhd.2016.05.004.

[13] 吴锋， 钟万勰. 浅水动边界问题的位移法模拟[J]. 计算机辅助工程， 2016， 25（2）： 5-13. DOI： 10.13340/j.cae.2016.02.002.

[14] WU F， ZHONG W X. On displacement shallow water wave equation and symplectic solution[J]. Computer Methods in Applied Mechanics and Engineering， 2017， 318： 431-455. DOI： 10.1016/j.cma.2017.01.040.

[15] 吴锋， 钟万勰. 浅水问题的约束Hamilton变分原理及祖冲之类保辛算法[J]. 应用数学和力学， 2016， 37（1）： 1-13. DOI： 10.3879/j.issn.1000-0887.2016.01.001.

[16] WU F， YAO Z， ZHONG W X. Fully nonlinear （2+1）-dimensional displacement shallow water wave equation[J]. Chinese Physics B， 2017， 26（5）： 54501. DOI： 10.1088/1674-1056/26/5/054501.

[17] 姚征， 鐘万勰. 位移法浅水波方程解的解及其特性[J]. 计算机辅助工程， 2016， 25（2）： 1-4. DOI： 10.13340/j.cae.2016.02.001.