基于CAXA的盘类凸轮CAD/CAM应用

解太林

传统的盘形凸轮廓形绘制主要有图解法和解析法，加工方法有手工画线加工和数控铣削加工，大批量生产亦可采用仿形铣。图解法直观、简单，但是手工作图选取的等分数有限、精度差。以此为基础的手工画线加工的精度和加工表面精度都比较低。解析法设计虽然解决了凸轮精度问题，但要得到完整的凸轮轮廓曲线就要编制复杂的程序。因此它的应用也就受到了很大的限制。利用CAD软件的强大作图功能，可以十分方便地进行凸轮的廓形设计，精度好效率高。本文介绍了利用CAXA系列CAD/CAM软件进行余弦盘形凸轮的绘制、编程与模拟加工。

一、建立数学模型

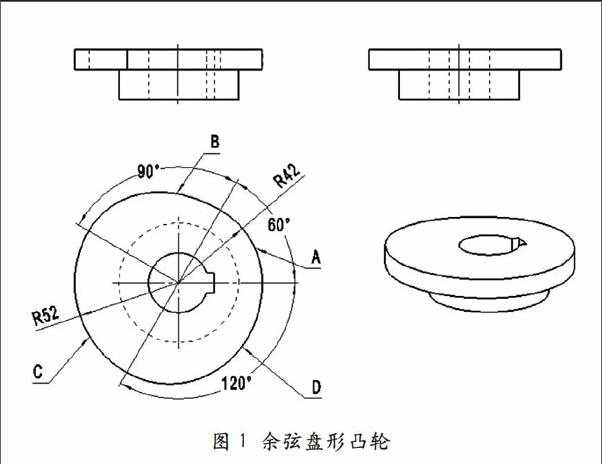
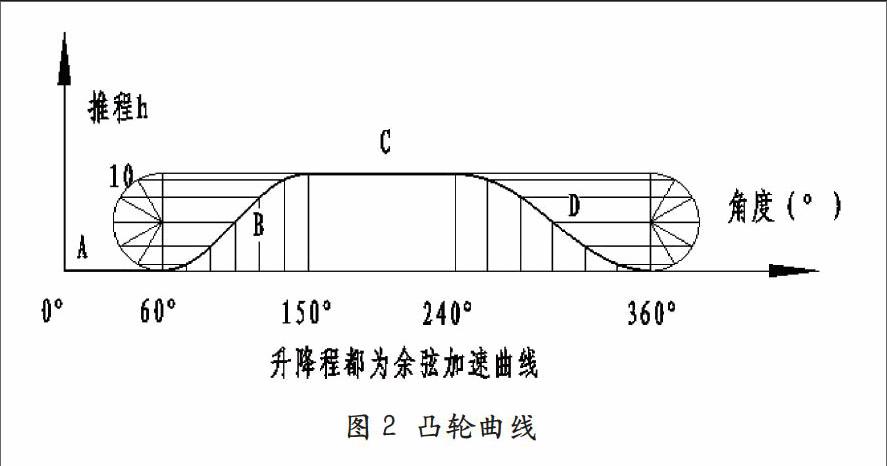
以图1余弦盘形凸轮为例，由图2凸轮曲线图可知，凸轮曲线由四段曲线组成，A段为R42圆弧，B段为升程余弦曲线，C段为R₅₂圆弧，D段为降程余弦曲线。余弦曲线的通用公式s=h[1-cos（πδ/δ%*p%*p₀%*b）]/2，其中s为推程，h为总推程，t为升程角，t₀为总升程角。

由图l所示，由图可知凸轮的基圆半径为42，而B段和D段余弦曲线升程起始角均不为0，故在作这两段余弦曲线时就不能直接套用通用公式。

如果设凸轮的基圆半径为r，余弦曲线升程起始角为t₁，那么，余弦曲线通用公式s=h[l-cos（πt/t₀）]/2就要变形为s=r+h[l-cos（π（t-t₁）/t₀）]/2，故可得B段余弦曲线公式和D段余弦曲线公式。

B段余弦曲线公式：

p（t）=42+（10*（1-cos（180*（t-60）/90））/2）

D段余弦曲线公式：

p（t）=52-（10*（1-cos（180*（t-240）/120））/2）

二、图解法绘制余弦盘形凸轮廓形

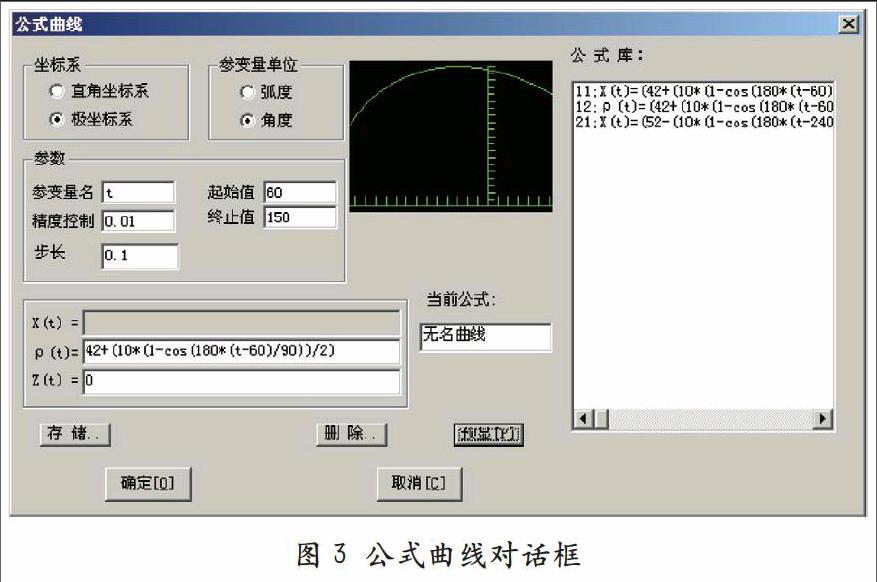
打开CAXA二维CAD软件后，点击公式曲线按钮，弹出如图4对话框，发现绘制曲线的方式有很多，这里主要介绍极坐标系/角度和直角坐标系/角度两种方法。

1.极坐标系/角度

（l）B段余弦曲线。

在图3对话框中填人参数t、p（t）和Z（t），这时在对话框预览中就出现了B段余弦曲线，然后可以点击确定按钮再点击CAD软件界面中的凸轮基圆圆心就可以了。

t=60-150

p（t）=42+（10*（1-cos（180*（t-60）/90））/2））

Z（t）=0

（2）D段余弦曲线。

在图4对话框中填人参数t、p（t）和Z（t），这时在对话框预览中就出现了D段余弦曲线，然后可以点击确定按钮，再点击CAD软件界面中的凸轮基圆圆心就可以了。

t=60-150

p（t）=52（10*（l-cos（180*（t240）/120））/2））

Z（t）=0

2.直角坐标系/角度

（1）B段余弦曲线。

在图5对话框中填人参数t、X（t）、Y（t）和Z（t），这时在对话框预览中就出现了B段余弦曲线，然后可以点击确定按钮，再点击CAD软件界面中的凸轮基圆圆心就可以了。

t=60-150

X（t）=（42+（10*（1-cos（180*（t60）/90））/2））*cos（t）

Y（t）=（42+（10*（1-cos（180*（t60）/90））/2））*sin（t）

Z（t）=0

（2）D段余弦曲线。

在图6对话框中填人参数t、X（t）和Y（t），这时在对话框预览中就出现了D段余弦曲线，然后可以点击确定按钮，再点击CAD软件界面中的凸轮基圆圆心就可以了。

t=240-360

X（t）=（52-（10*（1-cos（180*（t240）/120））/2））*cos（t）

Y（t）=（52-（10*（1-cos（180*（t-240）/120））/2））*sin（t）

三、用CAXA的CAM软件完成其加工

在CAXA中打开“加工”下拉菜单中，生成加工轨迹，如图7所示。最后，在“加工”下拉菜单，点击“模拟加工”，软件将进行动态模拟加工，如图8所示.