基于主S—N曲线法的T形接头疲劳评估和试验验证

俞壮壮 孙振轩

摘要：

以T形焊接接头为研究对象，将可能发生疲劳破坏的焊趾截面和焊喉截面的节点力转换为相对于中面焊线的等效节点力和弯矩，并利用平衡等效原理转化为线力和线弯矩，基于材料力学公式求出截面的结构应力，解决应力对网格尺寸敏感的难题。从焊缝疲劳破坏的机理出发，基于Paris断裂力学公式推导以等效结构应力为变量的一条主S-N曲线，评估焊缝的疲劳寿命。分析结果发现：采用主S-N曲线法评估的寿命与试验值最接近且破坏位置准确，该主S-N曲线法准确性较高。

关键词：

主S-N曲线； 焊趾； 焊喉； 疲劳； 网格敏感

中图分类号： TG405

文献标志码： B

Fatigue evaluation and test verification of T-shape joint

based on master S-N curve method

YU Zhuangzhuang， SUN Zhenxuan

（School of Traffic and Transportation Engineering， Dalian Jiaotong University， Dalian 116028， Liaoning， China）

Abstract：

Taken T-shape weld joint as object， the nodal stresses of weld toe cross section and weld throat section where fatigue damage may occur are converted to the equivalent nodal stress and bending moment related to middle surface welding line， and it is converted to line stress and line bending moment. The section structure stress is obtained based on material mechanics formula. The problem that the stress is sensitive on the mesh size is solved. Based on the Paris fracture mechanics formula， the master S-N curve taking equivalent structural stress as variable is derived to evaluate the weld fatigue life. The analysis results show that the fatigue life evaluated using the master S-N curve is the closest to the test value and the failure location is accurate. The accuracy of the master S-N curve method is high.

Key words：

master S-N curve； weld toe； weld throat； fatigue； mesh sensitivity

收稿日期： 2017-11-27

修回日期： 2017-12-19

作者簡介：

俞壮壮（1993—），男，山东聊城人，硕士研究生，研究方向焊接结构疲劳强度，（E-mail）huhuwai@vip.qq.com

0 引 言

焊接结构疲劳评估存在2个难点：一是有焊接结构的位置往往是结构刚度变化较大的地方，应力集中十分明显，常规有限元法计算的应力结果往往不精确；二是焊接接头的标准难以选择。国际焊接学会根据试验结果给出一组相互平行的S-N曲线，每一条曲线代表某种受载情况下的接头，这些曲线是疲劳寿命计算的依据。当应力变化范围Δσ确定后，选择不同的S-N曲线计算出的疲劳寿命差异很大，这就要求在选择S-N曲线时要充分考虑接头的几何情况和受载状况，但是在实际情况中很多焊接结构的几何形状十分复杂，受载情况也复杂多样，很难准确选择。主S-N曲线法是基于断裂力学基本原理和大量的接头疲劳试验提出的一种焊缝疲劳评估的新方法。此方法采用网格不敏感的结构应力法和一条S-N曲线，解决应力对网格的敏感性和焊接接头与S-N曲线难以一一对应的问题，提高焊缝疲劳评估的精度。基于结构应力的主S-N曲线方法已经被相关规范采纳[1]，并在实际工程中得到广泛应用。

1 主S-N曲线法

1.1 结构应力的定义和计算

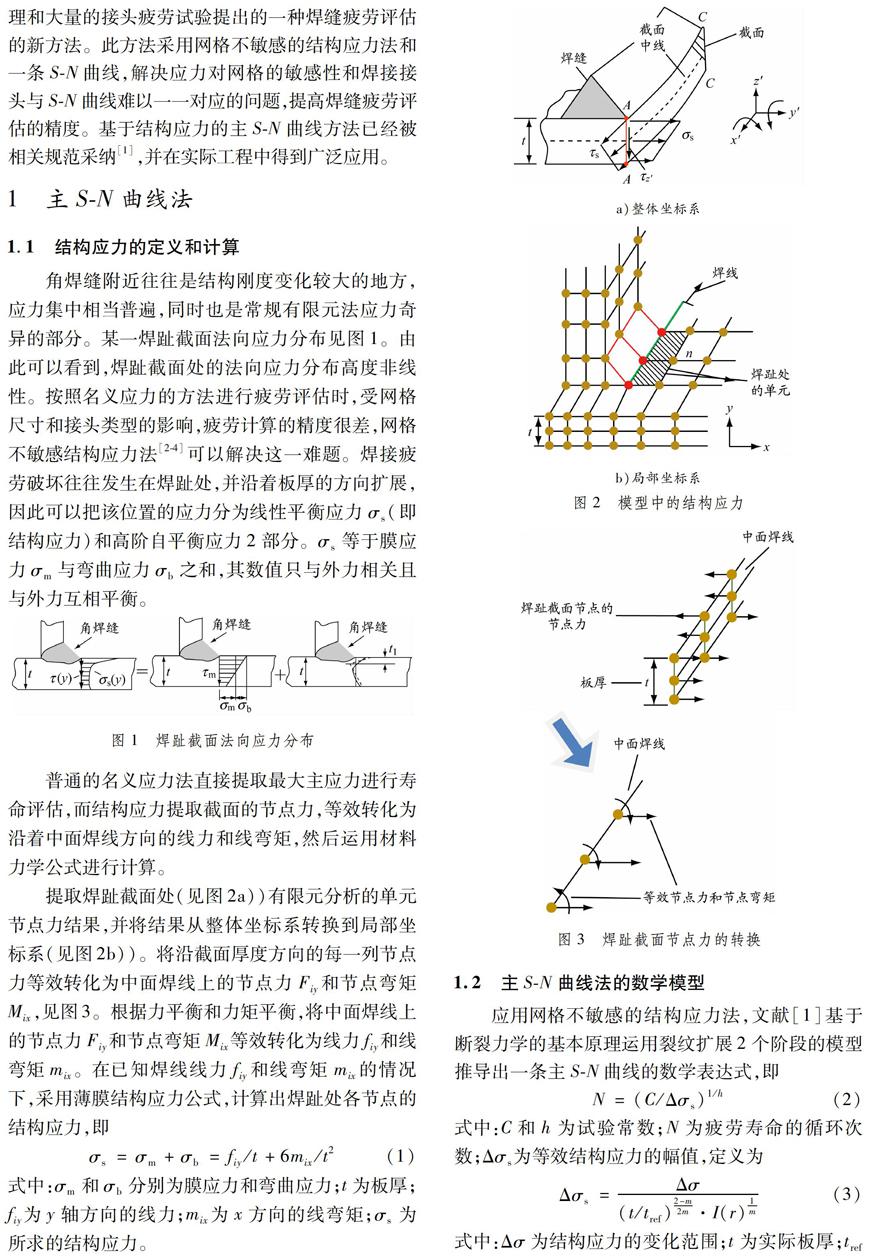
角焊缝附近往往是结构刚度变化较大的地方，应力集中相当普遍，同时也是常规有限元法应力奇异的部分。某一焊趾截面法向应力分布见图1。由此可以看到，焊趾截面处的法向应力分布高度非线性。按照名义应力的方法进行疲劳评估时，受网格尺寸和接头类型的影响，疲劳计算的精度很差，网格不敏感结构应力法[2-4]可以解决这一难题。焊接疲劳破坏往往发生在焊趾处，并沿着板厚的方向扩展，因此可以把该位置的应力分为线性平衡应力σs（即结构应力）和高阶自平衡应力2部分。σs等于膜应力σm与弯曲应力σb之和，其数值只与外力相关且与外力互相平衡。

图 1 焊趾截面法向应力分布

普通的名义应力法直接提取最大主应力进行寿命评估，而结构应力提取截面的节点力，等效转化为沿着中面焊线方向的线力和线弯矩，然后运用材料力学公式进行计算。

提取焊趾截面处（见图2a））有限元分析的单元节点力结果，并将结果从整体坐标系转换到局部坐标系（见图2b））。

将沿截面厚度方向的每一列节点力等效转化为中面焊线上的节点力Fiy和节点弯矩Mix，见图3。

根据力平衡和力矩平衡，将中面焊线上的节点力Fiy和节点弯矩Mix等效转化为线力fiy和线弯矩mix。

在已知焊线线力fiy和线弯矩mix的情况下，采用薄膜结构应力公式，计算出焊趾处各节点的结构应力，即

σs=σm+σb=fiy/t+6mix/t2 （1）

式中：σm和σb分别为膜应力和弯曲应力；t为板厚；fiy为y轴方向的线力；mix为x方向的线弯矩；σs为所求的结构应力。

a）整体坐标系

b）局部坐标系

图 2 模型中的结构应力

图 3 焊趾截面节点力的转换

1.2 主S-N曲线法的数学模型

应用网格不敏感的结构应力法，文献[1]基于断裂力学的基本原理运用裂纹扩展2个阶段的模型推导出一条主S-N曲线的数学表达式，即

N=（C/Δσs）1/h （2）

式中：C和h为试验常数；N为疲劳寿命的循环次数；Δσs为等效结构应力的幅值，定义为

Δσs=Δσ（t/tref）2-m2m·I（r）1m （3）

式中：Δσ为结构应力的变化范围；t为实际板厚；tref为单位板厚，取值为1；r为弯曲比，即弯曲应力占结构应力的比重；I（r）为表示载荷影响的函数；m为材料常数，取值为3.6。

虽然式（2）形式与其他普通的疲劳计算公式一样，分子为由试验确定的常数项，分母为由外载荷确定的应力幅值，但式（2）引入一个新的变量“等效结构应力幅值Δσs”。Δσs不仅考虑到应力集中的影响和载荷模式的影响，还考虑到焊接接头的板厚对疲劳寿命的影响。[5-6]

美国Battelle实验室分析1947年以来数千个焊接结构疲劳数据，这些焊接结构囊括不同的焊接接头、载荷状况和板厚等，取得很好的效果，可证明主S-N曲线的适用性。[7]

2 网格不敏感性证明

以无焊缝熔深的T形焊接接头为例，仿真试件基板的尺寸为270 mm×50 mm×20 mm，立柱尺寸为20 mm×50 mm×40 mm，焊脚尺寸为8 mm×8 mm。T形焊接接头几何模型见图4。施加载荷为25 200 N，4点加载，支撑跨距为270 mm，施加载荷跨距为100 mm。

图 4 T型焊接接头几何模型，mm

为证明不同网格尺寸对应力的影响，分别建立网格尺寸为2、4和6 mm的有限元模型见图5。分别对3种情况的最大主应力、von Mises应力和结构应力进行对比（见图6），并得出3種不同网格尺寸情况下右侧焊趾截面结构应力随焊线长度变化的曲线（见图7）。结果表明：随着网格尺寸的增大，最大主应力和von Mises应力降低十分明显，而结构应力并不以网格尺寸的变化而变化，体现出良好的网格不敏感性。

图 5 网络模型对比

图 6 不同尺寸网格计算出的应力对比

图 7 焊趾结构应力随焊线长度变化

3 不同评估方法对比

分别运用主S-N曲线法、名义应力法和热点应力法对T形接头进行疲劳寿命评估。名义应力法分别采用英国钢结构疲劳设计与评估标准[8]和国际焊接学会焊接接头及其部件疲劳设计标准[9]。热点应力法采用英国BS标准和IIW标准中的热点应力[8-9]计算。

对于T形接头，由于细节特征不同，其薄弱位置可能为焊趾截面或焊喉截面[10]（见图8），因基于结构应力的主S-N曲线法仅使用一条S-N曲线，故可以只对2个截面的等效结构应力进行比较。根据模型的几何结构和载荷特征，选取T形接头的右侧焊缝进行评估。

a）接头的截面定义

b）焊缝局部有限元模型

图 8 截面定义和局部有限元模型

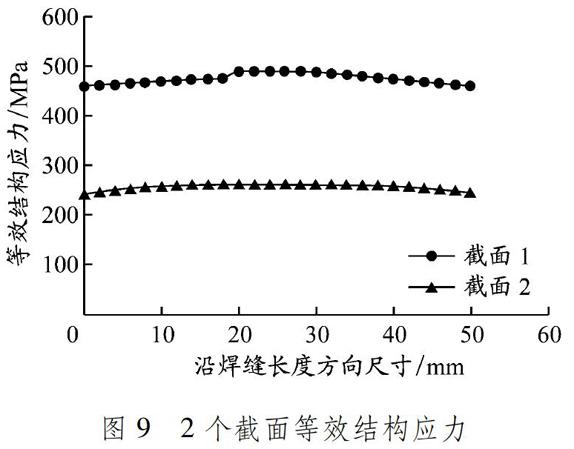
计算得到当前焊缝尺寸下2个截面的等效结构应力，见图9。由此可以发现：截面1的等效结构应力大于截面2的结构应力，因此截面1为当前焊缝的危险截面，此焊缝为焊趾破坏。

图 9 2个截面等效结构应力

采用不同评估方法得出的循环次数N见表1。因为工程中的疲劳寿命评估较为保守，所以计算-2σ存活率（98%）下的疲劳寿命。计算结果表明：采用主S-N曲线计算的寿命值明显大于其他方法，而且根据图7推测，疲劳破坏可能首先发生在焊缝的中部。

表 1 不同评估标准计算循环次数对比

4 仿真分析与试验对比

为检验基于主S-N曲线法评估疲劳的准确性，制作4个Q460钢制T形接头进行试验验证。为使疲劳试验的结果更偏向于工程实际，该批试件按照工厂实际生产的工艺参数进行自动化焊接。试验载荷F为28 000 N，应力比R为0.1，频率为4.2 Hz，4点加载。4个试验样本均为焊趾发生破坏，见图10。

a）

b）

图 10 试件损坏形式

发生疲劳破坏的平均循环次数N为99 384，标准差为23 538。按照正态分布统计，在存活率98%的情况下计算结果为52 308，试验结果见表2。试验统计结果与仿真分析的结果对比见图11。

使用主S-N曲线法评估得到的寿命与试验统计结果最为接近，与BS标准和IIW标准相比，主S-N曲线法准确度更高。

表 2 试验统计数据

图 11 仿真结果与试验结果对比

5 结 论

（1）基于网格不敏感的结构应力法，将焊趾截面或焊喉截面的节点力转换为相对于中面焊线的等效节点力和弯矩，再利用平衡等效原理转化为线力和线弯矩，然后基于材料力学公式求出截面的结构应力，最后基于Paris断裂力学表达式，推导出以等效结构应力为变量的一条主S-N曲线评估焊缝的疲劳寿命。

（2）对T形接头构建2、4和6 mm等3种不同网格尺寸的有限元模型，并分别进行应力计算，结果表明：3种应力中只有结构应力基本没有差值且分布规律基本一致；结构应力法体现出良好的网格不敏感性。

（3）分别采用名义应力法、热点应力法和结构应力法对T形接头进行疲劳评估，并与试验结果对比，结果发现在存活率98%时结构应力法的循环次数最大，与试验值最接近。网格不敏感的结构应力法评估疲劳的精度最高，值得在工程领域进行推广应用。

（4）主S-N曲线法可为焊接结构的抗疲劳设计提供新的理论方法。

参考文献：

[1] DONG P， HONG J K， OSAGE D A， et al. Master S-N curve method for fatigue evaluation of welded components[J]. Welding Research Council Bulletin， 2002（474）： 1-44.

[2] DONG P. A robust structural stress method for fatigue analysis of offshore/marine structures[J]. Journal of Offshore Mechanics and Arctic Engineering， 2004， 127（1）： 68-74. DOI： 10.1115/1.1854698.

[3] 兆文忠， 魏鸿亮， 方吉， 等. 基于主S-N曲线法的焊接结构虚拟疲劳试验理论与应用[J]. 焊接學报， 2014， 35（5）： 75-78.

[4] NIE C G， DONG P S. A traction stress based shear strength definition for fillet welds[J]. Journal of Strain Analysis for Engineering Design， 2012， 47（8）： 562-575.

[5] 武奇， 邱惠清， 王伟生. 基于结构应力的焊接接头疲劳分析[J]. 焊接学报， 2009， 30（3）： 101-106. DOI： 10.3321/j.issn：0253-360X.2009.03.026.

[6] 李向伟. 基于主S-N曲线法的焊接结构疲劳寿命预测系统开发和关键技术[J]. 计算机辅助工程， 2014， 23（4）： 46-52. DOI： 10.13340/j.cae.2014.04.010.

[7] 李向伟， 兆文忠. 基于Verity方法的焊缝疲劳评估原理及验证[J]. 焊接学报， 2010， 31（7）： 8-12.

[8] Code of practice for fatigue design and assessment of steel structures： BS 7608—1993[S].

[9] IIW Joint Working Group. Recommendations for fatigue design of welded joints and components： IIW-1823-07[S].

[10] 兆文忠， 李向伟， 董平沙. 焊接结构抗疲劳设计理论与方法[M]. 北京： 机械工业出版社， 2017： 23-25.