三通管内冷热掺混流动下的温度场预测

李泽伟 蒋彦龙 王合旭 陈冀 王瑞琪

摘要：

对三通管内冷热水的掺混流动过程进行试验研究，得到在30 ℃温差、不同进口流量比条件下掺混流域的温度场数据；提出基于BP神经网络的温度场预测模型，并将预测结果与实测数据进行对比。结果表明：掺混流域温度场特性的预测结果与试验数据吻合度较高，对温度振荡功率谱密度的分析也得到同样的结果，这对进一步研究管道热波动引起的管道热应力，以及进行管道热疲劳分析与寿命评估具有指导意义。

关键词：

三通管； 热掺混； 温度振荡； BP神经网络； 温度场预测； 功率谱密度

中图分类号： TM623

文献标志码： B

Temperature field prediction of cold and hot mixed flow

in three-way pipe

LI Zewei1， JIANG Yanlong1， WANG Hexu1， CHEN Ji1， WANG Ruiqi2

（

1. College of Aerospace Engineering， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China；

2. 609 Research Institute of Chinese Aeronautical Establishment， Nanjing 211106， China）

Abstract：

Test study on the cold and hot mixed flow in three-way pipe is carried out， and the temperature field data of mixing basin under 30 ℃ temperature difference and different inlet flow ratio is obtained； the temperature field prediction model based on BP neural network is proposed， and the prediction results are compared with measured data. The results show that the prediction of temperature field characteristics of mixing basin in mixing process is highly consistent with the test data. The same results of temperature oscillation power spectral density analysis are obtained. It is instructive to further study the thermal stress of pipes caused by thermal fluctuation， as well as thermal fatigue analysis and life evaluation.

Key words：

three-way pipe； thermal mixing； temperature oscillation； BP neural network； temperature field prediction； power spectral density

收稿日期： 2017-12-14

修回日期： 2018-01-12

基金项目：

南京航空航天大学研究生创新基地（实验室）开放基金（kfjj20170123）；中央高校基本科研业务费专项基金

作者简介：

李泽伟（1993—），男，山东胶州人，硕士研究生，研究方向为人机与环境工程和对流传热与传质，（E-mail）823023274@qq.com；

蒋彦龙（1977—），男，浙江金华人，教授，博导，研究方向为人机与环境工程，（E-mail）jiang-yanlong@nuaa.edu.cn

0 引 言

近年来，随着我国国民经济的持续增长和节能减排的迫切需求，能源结构调整迫在眉睫，核电作为一种经济高效、节能环保的新能源，發展迅猛。如何保障核电站建设和运行过程中的安全性和可靠性，是当下急需解决的首要问题之一。核电站拥有大量的热力管线，其中三通管连接各种管线，组成庞大的管路系统。当三通管的主管与支管流体温度不同时，就会在三通管下游段发生冷热水掺混，管道近壁面流体温度不断波动，使管材承受交变的温度载荷，诱发管道穿透裂纹，造成管道的热疲劳失效。[1]

国内外对三通管内冷热掺混展开大量的试验研究。MIYOSHI等[2]用148个热电偶测量三通冷热水掺混过程的壁面温度并计算热应力，认为：温度振荡范围主要集中在主管道内壁，应力的空间分布与壁面温度的空间分布相似；大应力波动由热点运动引起，运动频率约为0.1 Hz。KAMIDE等[3]利用热电偶和粒子图像测速技术测定三通冷热水掺混过程的温度场和速度场，将三通管内的流型分为壁射流、偏转射流和冲击射流等3类，对应各自的温度脉动曲线；当主、支管之间的动量比相同时，温度振荡的无量纲功率谱密度（power spectral density， PSD）相似。SELVAM等[4]研究在主管与支管恒定质量比为4∶1、温差分别为65和143 ℃工况下的热掺混特性，并与大涡模拟结果进行对比，平均温度、热波动和频率分布与实测数据均吻合较好，热波动的PSD没有表现出明显的特征频率，能量主要在0.1～2.0 Hz频率范围内。王海军等[5]对不同射流与主流流速比下三通管冷热水掺混过程进行研究，得到流动的基本特性以及不同流速比下局部点的温度振荡特性。

为评估核电管道的寿命，须测得管道的温度场，但核电管道中很难布置大量测温热电偶，需要从试验数据中寻找三通管内冷热掺混的特性及规律，并预测实际运行的核电三通管道冷热掺混过程中的温度场分布。只有掌握切实有效的温度场预测方法，才能进一步计算热波动引起的热应力，进行管道热疲劳分析与寿命评估。

在以往的研究过程中，研究者常用计算流体力学数值仿真模拟求解温度场，作为热应力分析的输入，但计算流体力学数值仿真计算中存在着许多误差，包括：控制方程简化误差、经验数据的误差、模型方程数值解的数值误差、边界条件与实测流量不完全一致所造成的误差等。[6]当一个含时间变量的控制方程组的初值有微小变化时，一段时间后结果会发生巨大变化，而更为复杂的N-S方程也会出现类似问题。

随着研究的不断深入，人工神经网络已广泛应用于模式识别、机器控制、预测估计等问题，国内外许多学者将人工神经网络应用在温度预测问题上。MATIC等[7]通过建立神经网络模型预测路面温度，ZHOU等[8]使用粒子群算法的BP神经网络预测电缆接头温度，张旭东等[9]建立BP神经网络模型预测纳卫星轨道温度。

本文采用BP神经网络方法对三通管内冷热掺混流动下的温度场进行

预测。BP神经网络是一种采用反向传播算法的多层感知机网络[10]，本质上可看作一种函数逼近器，三通管内冷热掺混过程中的温度场分布与进口参数之间必然存在一种函数关系，直接对这种函数关系进行理论分析难度巨大，而BP神经网络能够根据输入的进口参数与目标输出温度数据自行学习和存储这种函数映射关系，无须预先确定具体的函数关系。搭建三通管内冷热掺混试验系统，测量得到在30 ℃温差、不同进口流量比条件下掺混段管道近壁面流体温度，并采用一种基于BP神经网络的三通管内冷热掺混近壁面温度场预测方法，用试验得到的温度场数据训练BP神经网络，从而预测三通管内冷热掺混近壁面温度场分布情况。

1 试验过程

1.1 试验装置和方法

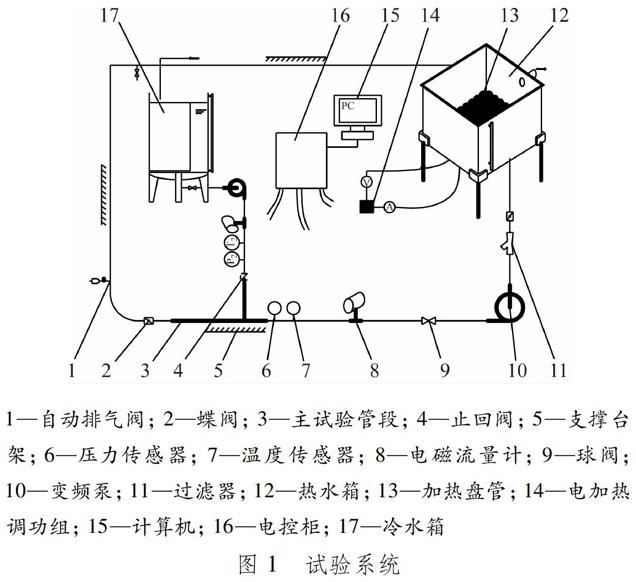
试验系统（见图1）采用水作为工质，由2条流动回路组成：一条为主管热水流动回路，另一条为支管冷水流动回路。采用一体化电控箱设计，由计算机的控制系统控制加热器、变频泵开关和工作功率，加热热水箱内的水，调节主管和支管的流量。流量计、温度传感器、压力传感器采集的数据都反馈到计算机中存储。

1—自动排气阀； 2—蝶阀； 3—主试验管段； 4—止回阀； 5—支撑台架； 6—压力传感器； 7—温度传感器； 8—电磁流量计； 9—球阀； 10—变频泵； 11—过滤器； 12—热水箱； 13—加热盘管； 14—电加热调功组； 15—计算机； 16—电控柜； 17—冷水箱

图 1 试验系统

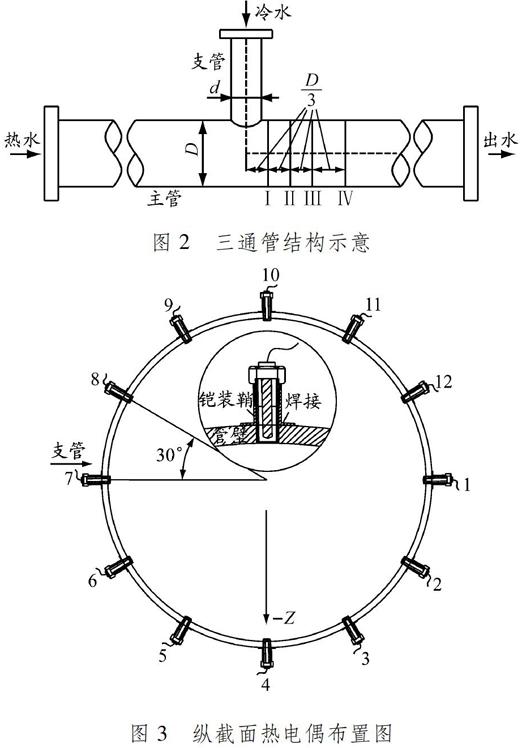
三通管结构示意见图2。

D为主管直径，取220 mm；d为支管直径，取98 mm；

主管与支管内径比为2.2。测温热电偶布置在主管道下游距离支管轴线D/3、2D/3、D、1.5D的Ⅰ～Ⅳ 这4个截面上。每个截面上以与主管轴线夹角间隔30°均匀安装有12个测温热电偶，7号热电偶为支管冷水射入方向，-Z为重力方向，纵截面热电偶布置见图3。热电偶铠装鞘焊接在管道钻孔中并做好密封处理。

图 2 三通管结构示意

图 3 纵截面热电偶布置图

首先用加热器加热主管回路和热水箱中的水，使其与支管回路冷水温差达到30 ℃；然后通过调节主管和支管回路中的变频泵来调节主管与支管流量比，并调节加热器功率使热水回路温度保持稳定，记录三通管内冷热水掺混整个过程中的管道近壁面温度数据。

1.2 试验结果和讨论

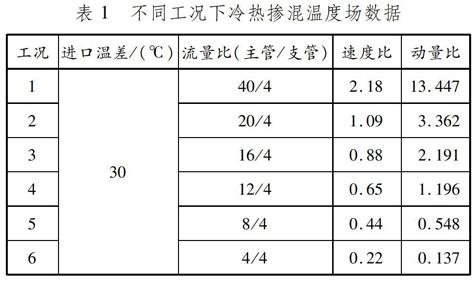
通过试验得到不同工况下冷热掺混温度场数据，见表1。在冷热水温差为30 ℃，主管与支管流量比为8/4，速度比为0.44的工况（工况5）下，截面Ⅰ～Ⅳ各有效测点的温度数据见图4。

表 1 不同工况下冷热掺混温度场数据

a） 截面Ⅰ

b） 截面Ⅱ

c） 截面Ⅲ

d） 截面Ⅳ

图 4 工况5条件下截面Ⅰ～Ⅳ各有效测点的温度

由图4可知：在掺混过程中，管道下游各测温截面上均表现出明显的温度振荡，其中主管内循环着热水，当支管内冷水射入主管时，受冷水射流影响较大的测点主要为1～3号和10～12号，这些测点温度发生明显下降，测点位置主要集中在与支管对面的一侧，说明冷水流穿过主管中心，已经影响到支管对面一侧的管壁附近，而支管一侧的7号测点受冷水射流影响较小，说明冷水射流核心区已远离支管一侧的近壁面，該处温度波动不明显。在截面Ⅰ和Ⅱ上，4、5、8、9号测点发生较强的周期性温度振荡，说明在支管一侧靠近管道上、下内壁面的位置，冷水射流破碎与主管热流混合，发生冷热水的传质；在截面Ⅲ和Ⅳ上，除支管一侧，基本整个内壁面测点都存在周期性的温度振荡，但振荡的幅度相比上游位置有所降低。横向来看，相同位置的测温点在不同截面上温度振荡的幅度不同，波动频率不同也使管道横向承受热应力，管壁纵向圆周和管壁横向都存在温度分布不均匀和温度振荡，引起管道的疲劳开裂。根据动量比计算公式

MR=4DρmV2mπdρbV2b（MR为主管与支管动量之比；ρm、ρb分别为主管和支管密度；Vm、Vb分别为主管和支管流速），在工况5条件下，计算动量比为0.548。根据KAMIDE等[3]的研究成果，当0.35

2 三通管内冷热掺混温度场预测模型的训练和验证

2.1 BP神经网络结构和算法

BP神经网络拓扑结构包括输入层、隐含层和输出层，见图5。层内神经元之间互不相连，相邻层间各神经元之间全连接，并用权值大小反映层间神经元之间的连接强度，其算法的核心思想是将输入数据正向传播，误差反向反馈以修改网络，不断迭代直至网络精度达到要求。选用单隐含层构建BP神经网络，隐含层使用Sigmoid函数作为传递函数。

图 5 BP神经网络拓扑结构

Sigmoid函数能识别高度非线性问题，输出层使用线性传递函数，分别为

f1（n）=11+e-n和f2（n）=n，n为传递函数的输入。BP算法通过将输入信号正向传播，误差反向传播，采用最陡梯度下降规则进行权值更新，使网络实际输出与期望输出均方误差最小，从数学角度阐释其原理[11]如下。

（1）输入信号为

p，BP神经网络共有M层，第m层权值、阈值、传递函数分别为

Wm、

bm、

fm，输入信号在各层间正向传播，

a为传递函数的输出，前一层输出

am又作为下一层的输入，各层输入与输出关系为

a0=

p

（1）

am+1=

fm+1（

Wm+1

am+

bm+1），m=0，1，…，M-1

（2）

a=

aM

（3）

nm+1=

Wm+1

am+

bm+1

（4）

（2）计算

a与期望输出

t的近似均方误差

（x）作为BP算法的性能指标。

（x）=（

t（k）-

a（k））T（

t（k）-

a（k））=

eT（k）

e（k）

（5）

式中：

e为期望输出与实际输出的误差。

（3） 定义

sm为

对m层输入的敏感性，敏感性反向传播，所以

sm=

nm

（6）

对式（6）进行矩阵推导，得

sM=-2

M（

nM）（

t-

a）

（7）

sm=

m（

nm）（

Wm+1）T

sm+1，m=M-1，…，2，1

（8）

（4） 采用最陡下降规则更新各层权值和阈值。

Wm（k+1）=

Wm（k）-α

sm（

am-1）T

（9）

bm（k+1）=

bm（k）-α

sm

（10）

式中：α为学习率。

（5） 迭代以上过程直到误差满足要求。

由于基本的BP算法存在收敛速度太慢和初始权值选取可能导致算法陷入局部极小点的问题，因此采用附加动量法和可变学习率法加强算法稳定性，提高算法学习速度。

2.2 建立预测模型

三通管内冷热掺混过程中温度场变化会受到流体温度和流动模式的影响，随时间周期性波动。王海军等[5]用速度比界定三通混流的流动模式，认为速度比不变时三通混流的流动模式也基本一致，但试验中并没有考虑管径变化对流动模式是否有影响；韩方军等[12]研究表明，不同管径比会对流动压力和流速产生影响；KOK等[13]用质量流量比界定流动模式，但忽略了密度对流动模式的影响；JUD等[14]研究2种密度比流体分层流动特性，得知密度对混合界面的界面深度、表面斜率和表面波动高度有影响。

采用动量比界定三通掺混的流动模式，综合管径、流体密度和速度比对流动模式的影响，具有更好的泛化能力。截取每个工况从掺混开始50～350 s时间段内的数据，此时掺混流动已经度过冷水刚射入主流时各测温点温度下降的阶段，温度的波动状态趋于稳定。输入层含有3个神经元，分别对应动量比、冷热水温差、时间这3个输入参数，根据Kolmogorov定理，当输入层神经元为m个时，隐含层神经元为2m+1个，足以逼近任意函数。选8个隐含层神经元，以加快网络训练过程中的收敛

速度。隐含层使用Sigmoid函数作为传递函数；输出层神经元数量为45个，对应45个温度测点的温度值。为验证温度场预测模型的预测效果，利用工况1、2、3、4、6的1 500组数据训练网络，工况5的300组数据进行验证。

2.3 结果对比及验证

三通管内冷热掺混温度场预测模型建立后，可输入动量比、温差和时间参数，得到对应的45个测点的温度值，将工况5的参数输入进预测模型中，得到在动量比为0.548、温差为30 ℃条件下300 s内的三通掺混温度场预测数据，并用试验实测数据验证预测模型的可靠性。选取不同截面上周期性温度振荡较为明显的不同位置（4、5、8、9号）测温点的预测和实测数据进行对比，预测结果与实测数据对比见图6。

a） 截面Ⅰ

b） 截面Ⅱ

c） 截面Ⅲ

d） 截面Ⅳ

图 6 预测结果与实测数据对比

由图6可知，各截面上不同位置测温点的预测结果与实测数据在温度振荡趋势和波动幅度方面均較吻合。截面Ⅰ、Ⅱ的5号和9号测温点的预测结果与实测数据PSD对比见图7。

PSD图可以显示在掺混过程中温度振荡的特征频率，由此可知：预测结

果与实测数据的PSD基本吻合，且可看出各点预测结果与实测数据主频率一致，均集中在0.02～0.05 Hz。由此可知，基于BP神经网络的温度场预测模型能够较好的对三通管内冷热掺混过程温度场进行预测。

a）截面Ⅰ

b）截面Ⅱ

圖 7 预测结果与实测数据PSD对比

3 结束语

通过搭建三通管内冷热掺混试验系统，测量不同进口流量比掺混下掺混流域管道近壁面温度数据，数据显示三通内冷热掺混过程中存在明显的周期性温度振荡。利用温度场数据对基于BP神经网

络建立的三通冷热掺混温度场预测模型进行训练，并用独立的试验数据对该模型进行验证。结果表明：对掺混过程中掺混流域温度场特性（包括温度振荡趋势和波动幅度等）的预测，与试验数据吻合度较高，对温度振荡PSD的分析也得到同样的结果。基于BP神经网络的温度预测模型的有效性得到验证，对进一步研究管道热波动引起的管道热应力，以及进行管道热疲劳分析与寿命评估具有指导意义。

参考文献：

[1]METZNER K J， WILKE U. European THERFAT project — thermal fatigue evaluation of piping system “Tee”-connections[J]. Nuclear Engineering and Design， 2005， 235（2-4）： 473-483. DOI： 10.1016/j.nucengdes.2004.08.041.

[2] MIYOSHI K， KAMAYA M， UTANOHARA Y， et al. An investigation of thermal stress characteristics by wall temperature measurements at a mixing tee[J]. Nuclear Engineering and Design， 2016， 298： 109-120. DOI： 10.1016/j.nucengdes.2015.12.004.

[3] KAMIDE H， IGARASHI M， KAWASHIMA S， et al. Study on mixing behavior in a tee piping and numerical analyses for evaluation of thermal striping[J]. Nuclear Engineering and Design， 2009， 239（1）： 58-67. DOI： 10.1016/j.nucengdes.2008.09.005.

[4] SELVAM K， KULENOVIC R， LAURIEN E， et al. Thermal mixing of flows in horizontal T-junctions with low branch velocities[J]. Nuclear Engineering and Design， 2017， 322： 32-54. DOI： 10.1016/j.nucengdes.2017.06.041.

[5] 王海军， 陈听宽， 罗毓珊， 等. T型三通管横向射流流动与传热实验研究[J]. 热能动力工程， 2002， 17（1）： 14-16. DOI： 10.3969/j.issn.1001-2060.2002.01.004.

[6] POPE S B. Turbulent flows[M]. Cambridge： Cambridge University Press， 2000.

[7] MATIC′ B， MATIC′ D， C′OSIC′ D， et al. A model for pavement temperature prediction at specified depth[J]. Metalurgija， 2013， 52（4）： 505-508.

[8] ZHOU H， WANG J， LIU K， et al. Temperature prediction study of cable joint conductor based on PSO algorithms of BP neural network[C]//Proceedings of 2015 IEEE International Magnetics Conference （INTERMAG）. Beijing： IEEE， 2015. DOI： 10.1109/INTMAG.2015.7157609.

[9] 张旭东， 李运泽. 基于BP神经网络的纳卫星轨道温度预测[J]. 北京航空航天大学学报， 2008， 34（12）： 1423-1427.

[10] SATISH K. 神经网络[M]. 北京： 清华大学出版社， 2006： 41-69.

[11] HAGAN M T， DEMUTH H B， BEALE M H. 神经网络设计[M]. 戴葵， 等译. 北京： 机械工业出版社， 2002： 11-24.

[12] 韩方军， 孙鑫， 张原. T型三通管内部流场数值模拟与结构优化[J]. 新疆水利， 2010（4）： 1-3.

[13] KOK B， VAROL Y， AYHAN H， et al. Experimental and computational analysis of thermal mixing characteristics of a coaxial jet[J]. Experimental Thermal and Fluid Science， 2017， 82： 276-286. DOI： 10.1016/j.expthermflusci.2016.11.028.

[14] JUD E， CRUA A， BLUMER U R. Experimental investigation of stratified flow in horizontal pipework of nuclear reactors[J]. Nuclear Engineering and Design， 1995， 153（2-3）： 173-181. DOI： 10.1016/0029-5493（95）90009-8.