优化端点条件的平面二次均匀B 样条插值曲线

李军成，刘成志，赵文才

（湖南人文科技学院数学与金融学院，湖南娄底 417000）

B 样条是目前大多数CAD 系统的基础模块，利用B 样条构造插值曲线是工程中经常遇到的问题。反求法是最为常用的一种利用B 样条构造插值曲线的方法，其基本思路是利用B 样条曲线满足的插值条件构造方程，通过求解方程反求B 样条曲线的控制顶点。为使方程存在唯一解，在利用反求法构造B 样条插值曲线时，往往需要补充端点条件。选取的端点条件不同，获得的插值曲线也不同。在实际应用中，端点条件的选取往往较困难。

在CAD 及其相关研究领域，构造光顺的曲线是一项重要的研究课题［1-3］。虽然目前尚无法定量描述曲线的光顺性，需通过能量极小构造平面光顺曲线［4］。例如，利用能量极小构造B 样条［5-6］、插值曲线 曲 面［7-8］、Hermite 插值［4，9-13］、Bézier 曲 线［14-16］、曲面网格［17-18］等。既然在反求法中端点条件为构造B样条插值曲线提供了自由度，那么很自然地想到可对端点条件进行优化，使得构造的B 样条插值曲线满足光顺性要求。

为此，通过极小化曲线的内能，获得具有较好效果的C1连续二次均匀B 样条插值曲线，且所构造的插值曲线是保形的。

1 预备知识

1.1 二次均匀B 样条曲线

给定平面上一列控制顶点pk(k=0，1，…，n)，二次均匀B 样条曲线可表示为［19］

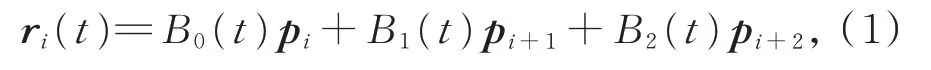
其中，i=0，1，…，n−2；0 ≤t≤1；Bj(t)为基函数，满足

二次均匀B 样条曲线段在端点处满足

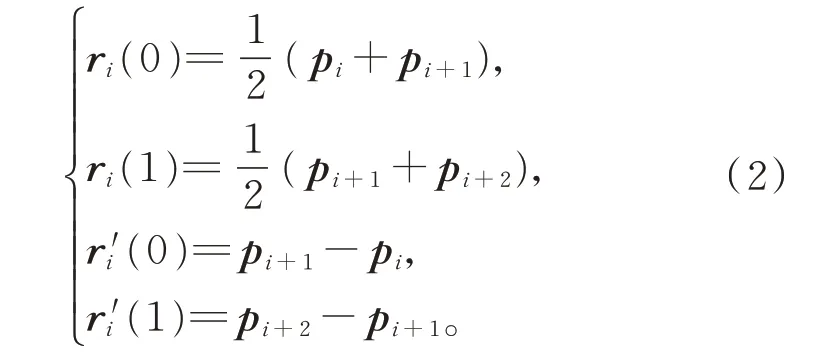
1.2 曲线的内能

拉伸能、应变能与曲率变化能是平面曲线内能的3 种常见形式，分别对应曲线的弧长、曲率和曲率变化率［6，14］。

给定平面参数曲线r(t)，其拉伸能、应变能与曲率变化能可分别定义为［14］

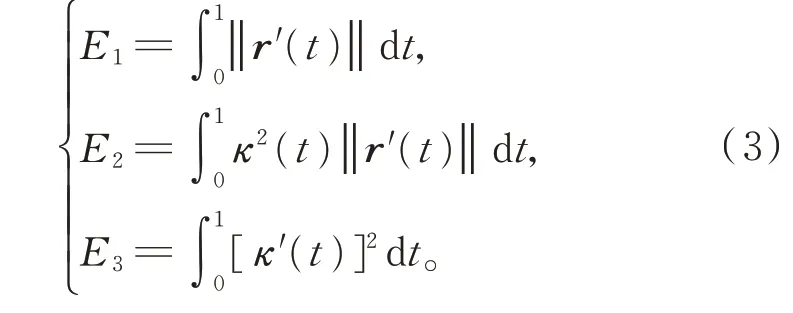
其中，κ(t)为曲线r(t)的曲率。

为简化计算，在实际应用中，常将式（3）近似地表示为［14］

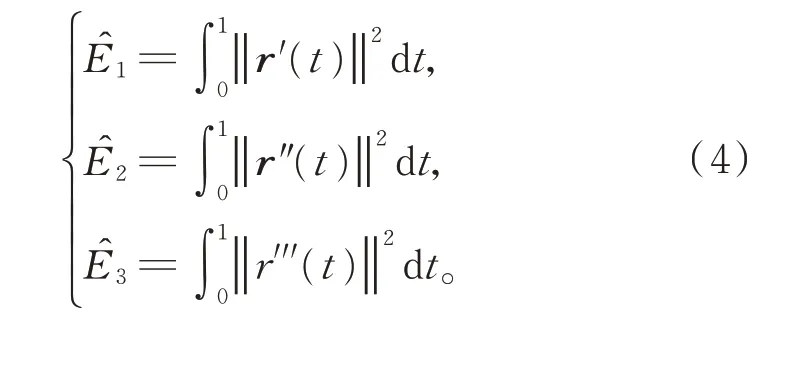
2 问题的提出

所要讨论的问题是：给定平面上n个数据点di(i=1，2，…，n)，如何构造一整条插值于给定数据点且满足C1连续的二次均匀B 样条插值曲线r(t)={ri(t)，i=0，1，…，n−2}。

由式（1）知，要构造插值曲线r(t)，只需确定各段曲线ri(t) (i=0，1，…，n−2)的控制顶点pk(k=0，1，…，n)。由式（2）知，要使曲线r(t)插值于数据点di(i=1，2，…，n)，则必有

由式（5）可得

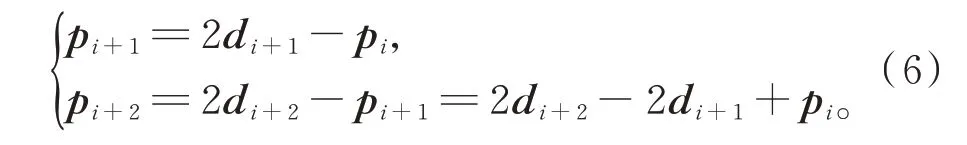
式（6）表明，只要确定了控制顶点p0，便可依次确定其他控制顶点pi(i=1，2，…，n)，或只需确定控制顶点pn，也可依次确定其他控制顶点pn−i(i=1，2，…，n)，这种确定插值曲线控制顶点的方法也称为反求法，p0或pn称为端点条件。由于二次均匀B样条曲线具有对称性［19］，故将p0或pn作为端点条件确定的二次均匀B 样条插值曲线是完全相同的。下面仅讨论将p0作为端点条件的情形。

事实上，当控制顶点p0给定时，控制顶点pi(i=1，2，…，n)可由以下定理确定。

定理1给定控制顶点p0，控制顶点pi(i=1，2，…，n)可表示为

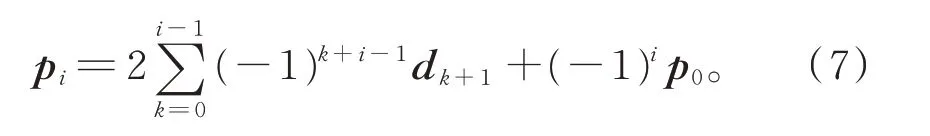
证明用数学归纳法证明。

当i=1 时，由式（6），可得式（7）。 假设当i=m时，有

则当i=m+1 时，由式（6）知

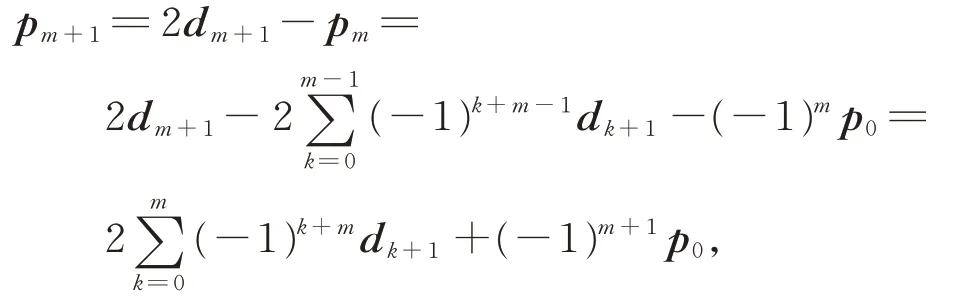
即式（7）成立。

证毕。

由定理1 可知，插值于数据点di(i=1，2，…，n)的C1连续二次均匀B 样条插值曲线r(t)={ri(t)，i=0，1，…，n−2}仅由控制顶点p0（即端点条件）决定。理论上，可通过选取不同的控制顶点p0使插值曲线满足不同需求。当然，也可优化选取控制顶点p0，使构造的C1连续二次均匀B 样条插值曲线满足特定要求。

下面讨论如何利用内能极小优化选取控制顶点p0，构造光顺的C1连续二次均匀B 样条插值曲线。

3 利用内能极小优化端点条件

由于对二次均匀B 样条曲线求三阶导数后归零，故只讨论如何通过拉伸能极小与应变能极小优化选取控制顶点p0，构造光顺的C1连续二次均匀B样条插值曲线。

3.1 利用拉伸能极小优化端点条件

由式（6），式（1）可改写为

由式（8）可得

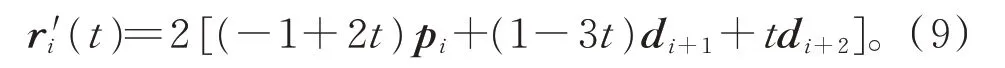
由式（4）与式（9），插值曲线r(t)={ri(t)，i=0，1，…，n−2}的拉伸能可表示为

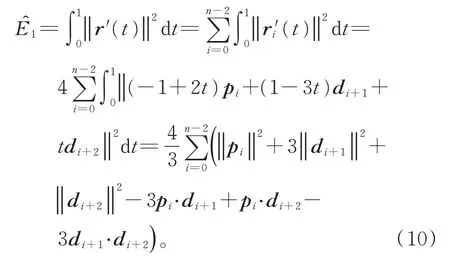
由式（7）知，在式（10）中仅p0为自由变量。因此，为确定最优的p0，插值曲线须具有极小拉伸能，得到无约束优化问题

为求解问题（11），首先给出以下引理。

引 理 1设 向 量a=(ax，ay)，记则有

证明令向量b=(bx，by)，由于a⋅b=axbx+ayby，故有

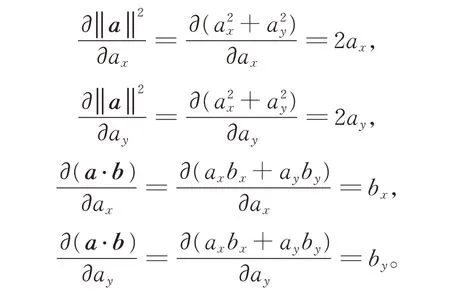
从而有，

于是，由式（7）和式（12），可得

证毕。

定理2要使插值于数据平面上的数据点di(i=1，2，…，n)的C1连续二次均匀B 样条插值曲线r(t)={ri(t)，i=0，1，…，n−2}具有极小拉伸能，控制顶点p0应为

证明当n=2 时，由引理1 和式（10），可得

当n＞2 时，由引理1 和式（10），可得

证毕。

3.2 利用应变能极小优化端点条件

式（8）经计算可得

由式（4）和式（16），插值曲线r(t)={ri(t)，i=0，1，…，n−2}的应变能可表示为

由式（7）可知，在式（17）中仅控制顶点p0为自由变量。为确定最优的p0使得插值曲线具有极小应变能，可得无约束优化问题

定理 3给定平面上的数据点di(i=1，2，…，n)，具有极小拉伸能的C1连续二次均匀B样条插值曲线r(t)={ri(t)，i=0，1，…，n−2}也具有极小应变能。

证明当n=2 时，由引理1 和式（17），可得

当n＞2 时，由引理1 和式（17），可得

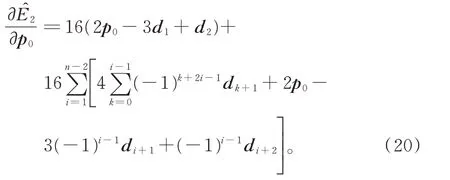
由定理2 可知，当插值曲线r(t)具有极小拉伸能时，控制顶点p0应满足式（13）。将式（13）代入式（19）和式（20），可得，故式（13）也为式（18）的解。因此，具有极小拉伸能的C1连续二次均匀B 样条插值曲线也具有极小应变能。

证毕。

3.3 保形插值

在数据插值中，保形插值一直以来深受重视［20-22］。若给定平面上的数据点di(i=1，2，…，n)，设s(t)：=si(t)=(1−t)di+tdi+1，0 ≤t≤1，显然线性插值s(t)是一种最简单的保形插值［23］。要使插值于数据点di(i=1，2，…，n)的C1连续二次均匀B样条插值曲线r(t)={ri(t)，i=0，1，…，n−2}具有良好的保形性，须对控制顶点p0进行优化，使得r(t)尽可能地接近s(t)，于是，得到无约束优化问题

定理4给定平面上的数据点di(i=1，2，…，n)，具有极小拉伸能或极小应变能的C1连续二次均匀B 样条插值曲线r(t)={ri(t)，i=0，1，…，n−2}为保形插值。

证明由式（8），经计算可得

当n=2 时，由引理1 和式（22），可得

当n＞2 时，由引理1 和式（22），可得

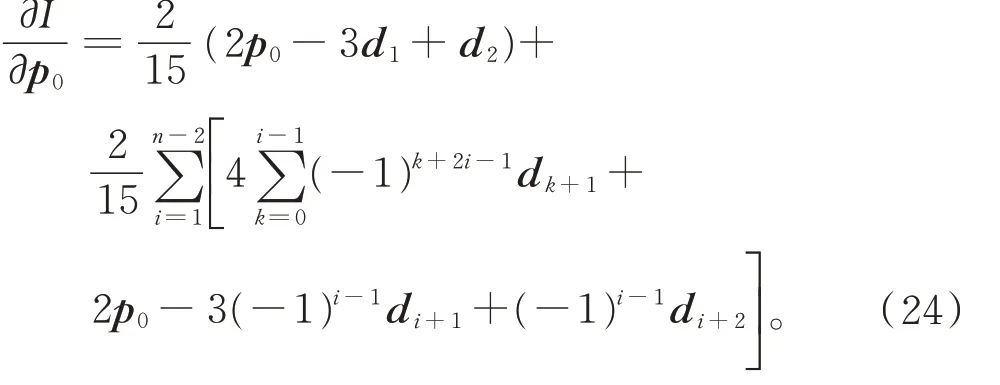
由定理2 可知，当插值曲线r(t)具有极小拉伸能时，控制顶点p0应满足式（13）。将式（13）代入式（23）和式（24），可得=0，故式（13）也为问题（21）的解。因此，具有极小拉伸能的C1连续二次均匀B 样条插值曲线为保形插值。由定理3 可得，具有极小应变能的C1连续二次均匀B 样条插值曲线也为保形插值。

证毕。

综上，利用拉伸能极小或应变能极小构造光顺的C1连续二次均匀B 样条保形插值曲线算法的步骤为：

算法1利用拉伸能极小或应变能极小构造C1连续二次均匀B 样条保形插值曲线。

步骤1输入数据点di(i=1，2，…，n)。

步骤2利用式（13）计算控制顶点p0。

步骤3利用式（7）计算控制顶点pi(i=1，2，…，n)。

步骤4由式（1）生成C1连续二次均匀B 样条插值曲线r(t)={ri(t)，i=0，1，…，n−2}。

4 数值算例与应用

下面通过几个数值算例说明本文算法的有效性。

例1给定数据点

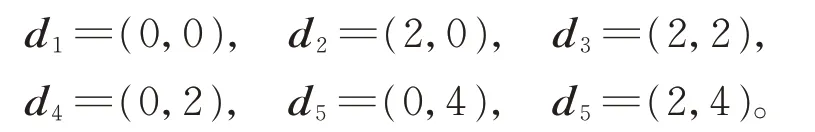
不同控制顶点p0所对应的C1连续二次均匀B 样条插值曲线如图1 所示。

由图1 可知，选取的控制顶点p0不同，所构造的插值曲线也不同。当p0选取不恰当时，构造的插值曲线也不理想，如图1（a）所示。在实际应用中，控制顶点的选取往往比较困难，此时可利用本文算法构造光顺的保形插值曲线，见图2。由式（13），可得p0=(−1，2)。

由图2 可知，本文算法构造的插值曲线较图1（a）中的插值曲线效果更好，较图1（b）中的插值曲线保形性更好。

图1 不同控制顶点p0 所对应的插值曲线Fig.1 The interpolation curves with different p0

图2 光顺的保形插值曲线Fig.2 The fairing shape-preserving interpolation curve

例2设数据di=(xi，yi)取自函数

由式（13），经计算可得p0=(0.130 0，152.760 1)，由本文算法构造的插值曲线（实线）及原函数曲线（虚线）如图3 所示。由图3 知，利用本文算法构造的插值曲线能较好地逼近函数，且具有较好的保形性。

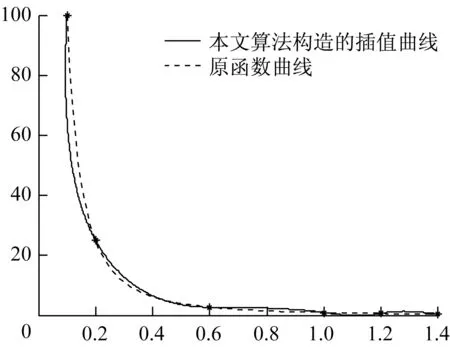
图3 插值于函数的光顺保形曲线Fig.3 The fairing shape-preserving curve interpolating the functional

例3考虑封闭插值曲线情形。设数据di=(xi，yi)取自单位圆

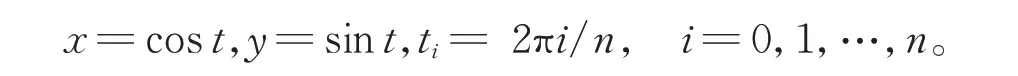
当n=4 时，由式（13）可得p0=(1，−1)；当n=8 时，由式（13）可得p0=(1，−0.414 2)。由本文算法构造的插值曲线（实线）及单位圆曲线（虚线）如图4所示。

图4 插值于单位圆的光顺保形曲线Fig.4 The fairing shape-preserving curve interpolating the unit circle

由图4 可知，即使给定的数据点只有5 个，利用本文算法构造的插值曲线也能较好地逼近单位圆；当给定的数据点为9 时，利用本文算法构造的插值曲线与单位圆几乎重合。

例4考虑特定曲线情形。图5 为利用本文算法生成的α型插值曲线和β型插值曲线，其中β型插值曲线由2 段插值曲线合成。

图5 特定曲线造型Fig.5 The specific curve modeling

为便于实际应用，在MATLAB 平台上设计了算法所对应的图形用户界面（graphical user interface，GUI）。该GUI 主要由生成插值曲线、保存插值曲线、清除数据等按钮，以及输入插值数据点坐标、插值曲线等显示框组成，如图6 所示。

图6 GUIFig.6 The graphical user interface

用户只需在界面指定位置输入插值数据点坐标，点击相应按钮即可生成、保存光顺的C1连续二次均匀B 样条保形插值曲线，如图7 所示。

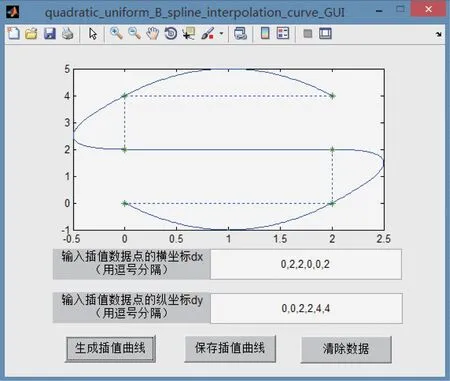
图7 GUI 演示1Fig.7 The graphical user interface demo 1

用户也可在界面指定位置输入插值数据点的横坐标，利用给定函数计算相应纵坐标，点击相应按钮即可生成、保存逼近于给定函数的光顺C1连续二次均匀B 样条保形插值曲线，如图8 所示。

图8 GUI 演示2Fig.8 The graphical user interface demo 2

5 结 语

为构造C1连续二次均匀B 样条插值曲线，首先给出了二次均匀B 样条插值曲线的分控制顶点与首个控制顶点（即端点条件）的递推关系式，然后分别利用拉伸能极小和应变能极小对首个控制顶点进行优化选取，从而构造光顺的插值曲线。事实表明，具有极小拉伸能的C1连续二次均匀B 样条插值曲线也具有极小应变能，且所构造的插值曲线为保形插值。进一步，给出了基于MATLAB 平台设计的GUI，用户只需输入插值数据点坐标并点击按钮即可获得光顺的C1连续二次均匀B 样条保形插值曲线。本文算法及给出的GUI 为B 样条插值曲线的构造提供了新选择。同时注意到，本文只给出了适用于构造C1连续二次均匀B 样条插值曲线的算法，若要构造更高次数或满足更高连续性要求的均匀B样条插值曲线，则需要推导分控制顶点与端点条件之间的递推关系，有待下一步研究。