带2 个形状参数的多项式可展曲面造型
王海波,杨当福,佘卫勤,刘圣军,刘新儒*,陈月安,白燕羽
(1.中南大学工程建模与科学计算研究所,湖南长沙 410083;2.中国航发南方工业有限公司,湖南 株洲 12000)
0 引 言
随着计算机技术的发展,计算机辅助几何设计在机械、航空、建筑等领域得到了广泛应用,曲线曲面表示方法作为计算机辅助几何设计中的重要方法[1],广受学者关注。在曲线曲面表示方法中,基函数的构造尤为重要。
传统的Bézier 基函数、B 样条基函数虽然具有很多优良性质,但一旦曲线曲面的控制顶点确定,其形状也随之确定,而在实际应用中,往往需要对曲线曲面的形状进行微调。文献[2]将权因子引入有理Bézier 曲线,文献[3-4]在线性无关的三角函数生成空间中,构造了带参数的三角Bézier 基函数,通过调节权因子或参数达到调节曲线形状的目的。与有理基函数、三角Bézier 基函数相比,多项式基函数具有易于求导、计算简便等优点。文献[5-8]构造了一系列带形状参数的扩展Bézier 基函数,增加了曲线曲面的自由度,便于调节形状。此外,求插值于给定数据点的Bézier 曲线或B 样条曲线通常通过求解线性方程组实现,此方法虽然可满足曲线光顺、保凸等要求,但求解线性方程组的工作量较大。文献[9-14]分别基于不同的基函数(包括(有理)多项式插值样条基函数、(有理)三角插值样条基函数)构造了保形插值曲线,并推导了形状参数和局部参数的约束条件。另外,通过调节参数大小,可获得光顺性更好的插值曲线。
可展曲面因其独特的性质在工业设计与制造中应用广泛。现有的可展曲面设计方法主要有2 种:(1)将可展曲面看作直纹面的特殊情况,予张量积直纹面以一定的约束,求解特征方程组[15-17];(2)利用点面几何的对偶性设计可展曲面[18]。第1 种方法所形成的特征方程组通常呈非线性,求解较困难;第2 种方法在调节可展曲面的形状上有一定欠缺。文献[19-23]在第2 种方法基础上,构造了一系列带形状参数的可展曲面,一定程度上弥补了第2 种方法的不足。
本文提出一种新的带2 个形状参数的四次多项式基函数。该基函数具有较好的形状调节能力和良好的性质。特别地,当2 个形状参数都等于0 时,该基函数就退化为三次伯恩斯坦基函数。利用此基函数,构造了G1连续插值样条,并讨论了样条曲线的保形性。另外,基于对偶性原理,设计了可展曲面,讨论了构造G0、G1、G2和G3连续曲面时参数的选取条件。最后,用具体实例进行了说明。
1 带2 个形状参数的多项式基函数
定义1对任意的t∈[0,1],λ1,λ2∈[0,1],

为带2 个形状参数λ1,λ2的四次多项式基函数。
1.1 基函数的性质
(ⅰ)退化性:当λ1=λ2=0 时,式(1)退化为三次伯恩斯坦基函数。
(ⅱ)非负性:对任意的λ1,λ2∈[0,1],有Fi,4(t) ≥0,i=0,1,2,3。
证明将式(1)改写为

其 中,Bi,4(t)(i=0,1,…,4)为四次伯恩斯坦基函数,当λ1,λ2∈[0,1]时,矩阵A的元素均非负,而四次伯恩斯坦基函数也非负,故对任意的λ1,λ2∈[0,1],均有Fi,4(t) ≥0,i=0,1,2,3。
(ⅲ)归一性:对任意的λ1,λ2∈[0,1],有
(ⅳ)端点性:对任意的λ1,λ2∈[0,1],有
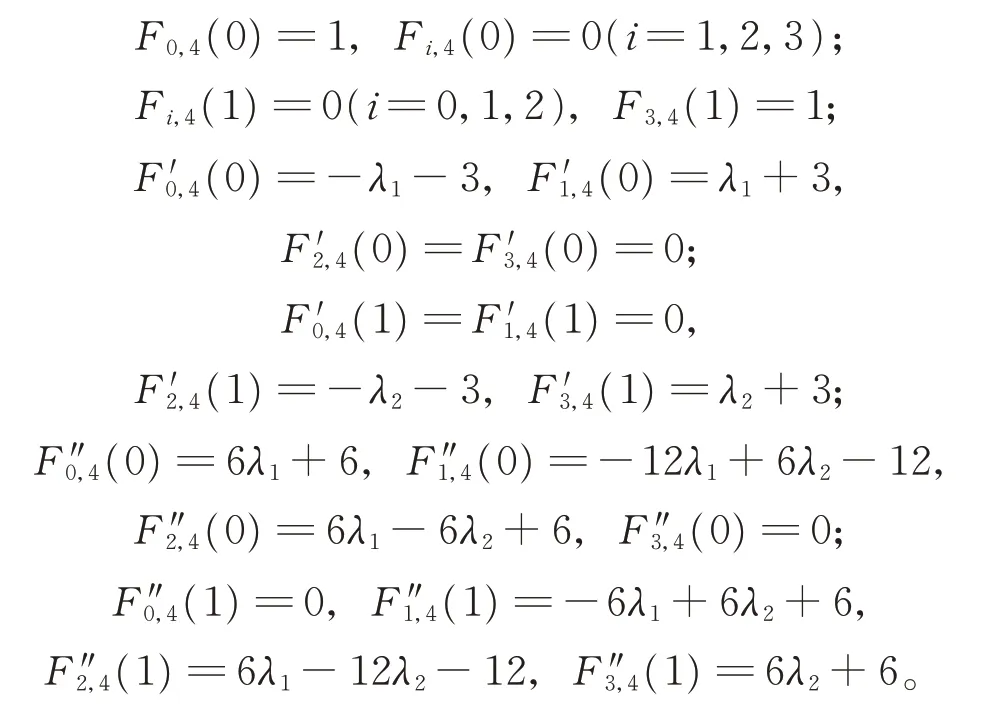
(ⅴ)对称性:当λ1=λ2时,有

(ⅵ)线性无关性:对任意的λ1,λ2∈[0,1],Fi,4(t) (i=0,1,2,3)线性无关。
1.2 逼近性质及形状控制
定义 2给定 4 个控制顶点Pi∈Ru(u=2,3;i=0,1,2,3),带2 个形状参数的曲线表达式为
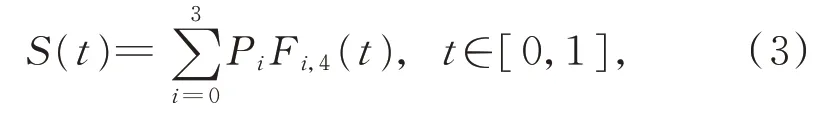
其 中,λ1,λ2∈[0,1],Fi,4(t) (i=0,1,2,3)为 式(1)中定义的基函数。
对任意的λ1,λ2∈[0,1],该曲线有以下性质:
(ⅰ)端点性
端点满足:

端点导数满足:

端点二阶导数满足:

(ⅱ)对称性

(ⅲ)凸包性
所生成的曲线始终位于Pi∈Ru(u=2,3,i=0,1,2,3)所构成的凸包内。
(ⅳ)变差减少性
除包含控制多边形的整个平面外,任意平面与该曲线的交点数均不会超过该曲线与控制多边形的交点数。
(ⅴ)平移与仿射不变性
该曲线满足

其 中,为Ru(u=2,3)中的任意向量,H为任意u×u(u=2,3)阶矩阵。
(ⅵ)形状可调性
该曲线的2 个形状参数λ1,λ2∈[0,1],增加了曲线的自由度。
形状调节可视化效果如图1 所示,其中,黑实线表示控制多边形,图1(a)中,λ2=0,红、绿、蓝、黄、黑、青 虚 线 分 别 表 示λ1=0,0.2,0.4,0.6,0.8,1.0;(b)中,λ1=0,红、绿、蓝、黄、黑、青虚线分别表示λ2=0,0.2,0.4,0.6,0.8,1.0;(c)中,λ1+λ2=1,红、绿、蓝、黄、黑、青 虚 线 分 别 表 示λ1=0,0.2,0.4,0.6,0.8,1.0;(d)中,λ1=λ2,红、绿、蓝、黄、黑、青 虚线分别表示λ1=λ2=0,0.2,0.4,0.6,0.8,1.0。 由图 1 可知,对于固定的t(t∈[0,1]),当只增大λ1时,曲线向控制顶点P2偏移;当只增大λ2时,曲线向控制顶点P1偏移;当增大λ1、减小λ2时,曲线向控制顶点P2偏移;当同时增大λ1和λ2时,曲线向控制多边形靠近。
1.3 保正插值及条件
定义3给定一组数据点(xi,yi)(i=1,2,…,n),其中,x1<x2<…<xn,四次插值样条为
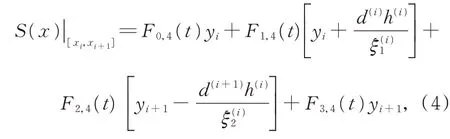
其中,Fj,4(t)(j=0,1,2,3)为式(1)定义的基函数,为插值曲线在xi处的导数值,基于文献[11]中的算术平均方法即式(4)计算得到。记区间[xi,xi+1] (i=1,2,…,n−1)上 的 第i条 曲 线 段为s(i)(x)。

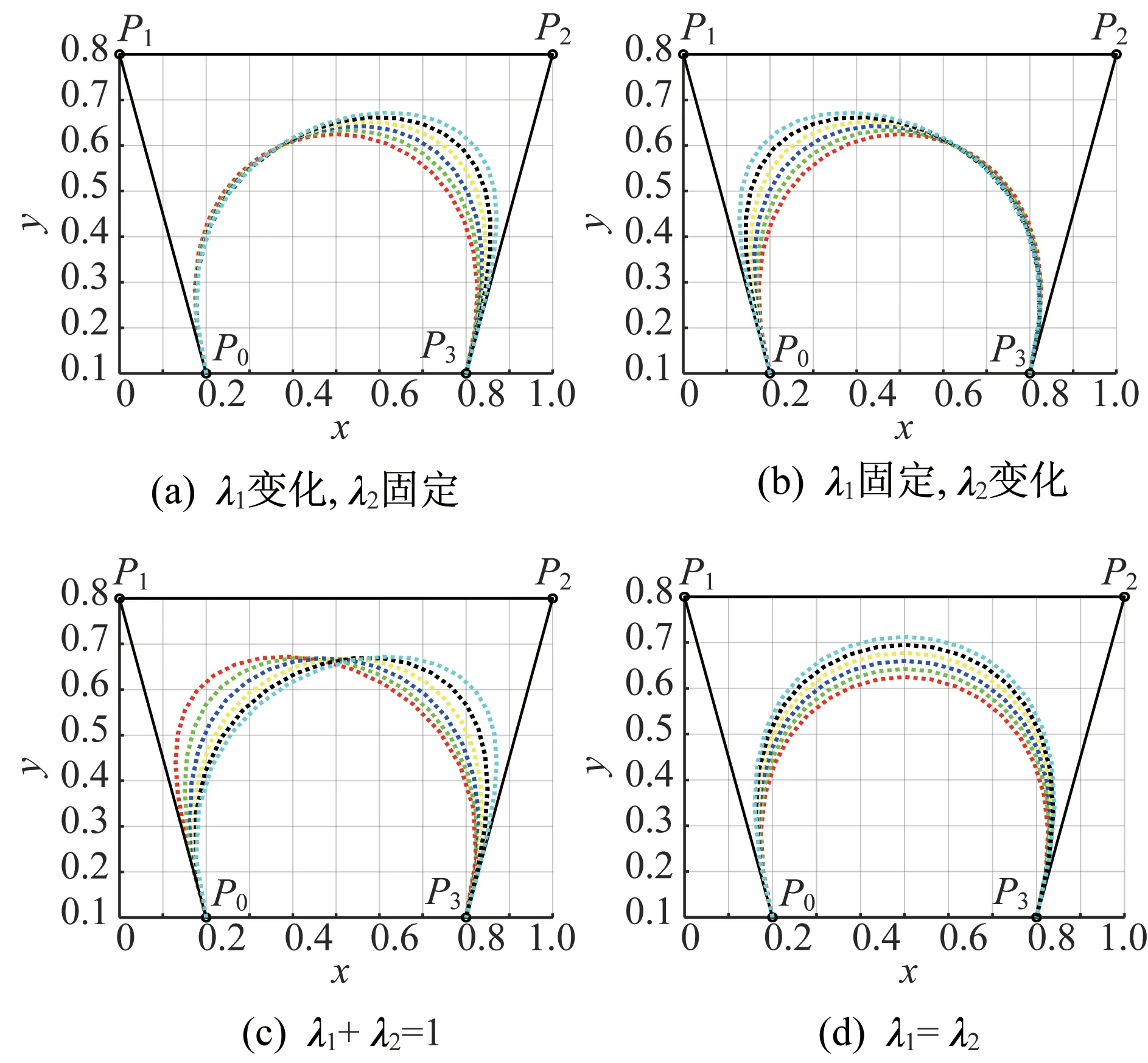
图1 形状参数对曲线的调节作用Fig.1 The adjustment effect of shape parameters on the curve
由基函数的端点性质和式(4)、式(5),有
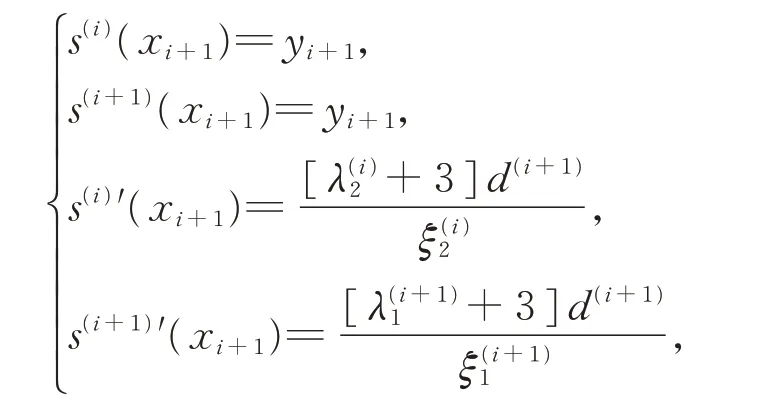
其中,i=1,2,…,n−1。则S(x)插值于所有给定的数据点,而且在相邻曲线段的连接点处可达G1连续。
对于给定的数据点(xi,yi)(i=1,2,…,n),若yi>0(i=1,2,…,n),使 得S(x)>0,x∈[x1,xn],则称插值曲线具有保正性。
不失一般性,考虑区间[xi,xi+1]上的曲线段s(i)(x)(i=1,2,…,n−1)。利用式(2),将式(4)改写为
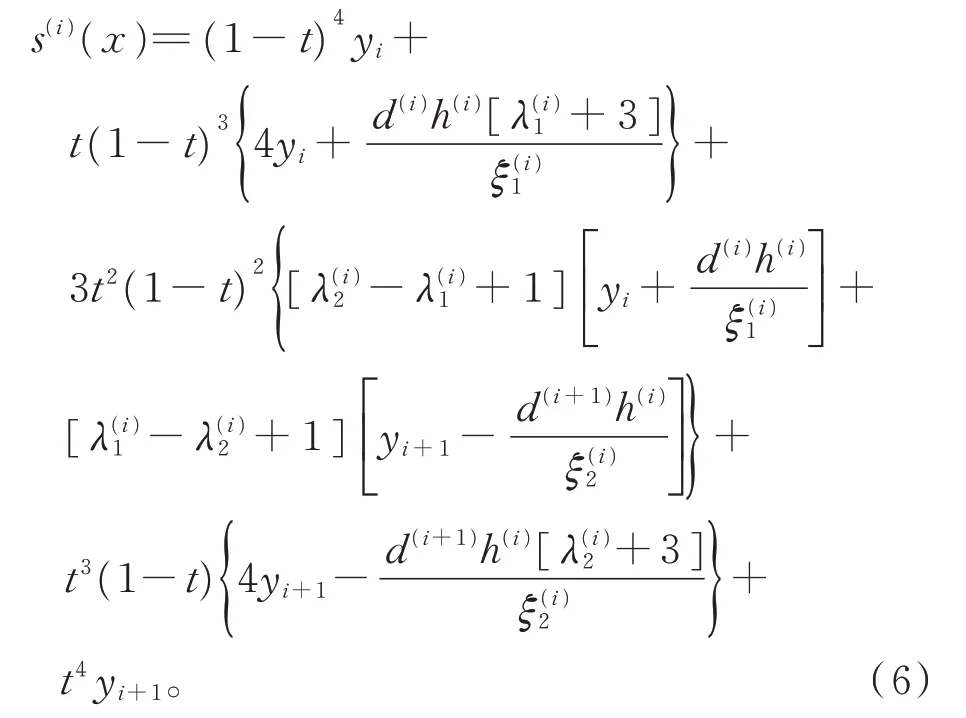
由yi>0(i=1,2,…,n)及式(6),可得使s(i)(x)>0成立的充分条件为


时,有S(x)>0,x∈[x1,xn]。 通过调节可使曲线更加光顺。
1.4 保单调插值及条件
式(4)所定义的插值样条不仅具有保正性,而且在一定条件下还具有保单调性。下面分析插值样条的保单调性及其条件。
对于给定的单调数据点(xi,yi)(i=1,2,…,n),即yi+1≥yi或yi+1≤yi(i= 1,2,…,n−1),x∈[x1,xn],使得S′(x)≥0,则称插值曲线具有保单调性。本文只考虑数据点单调递增的情况,数据点单调递减的情况类似可证。
不失一般性,考虑在区间[xi,xi+1]上的曲线段s(i)(x)(i=1,2,…,n−1),对 式(6)求导,经整理可得

当yi+1≥yi(i=1,2,…,n−1),即Δi≥0 时,由 式(5)可 知,d(i)≥0,故由式(8),得到满足S′(x)≥0(x∈[x1,xn])的充分条件为

(ⅰ)当满足Δi=0,时,有di=di+1=0,则对任意的均 有s(i)′(x)=0,并且在区间[xi,xi+1]上的曲线段s(i)(x)=yi=yi+1。

时,有S′(x)≥0(x∈[x1,xn])。


由式(10)和式(11)可知,当Δi>0 时,取
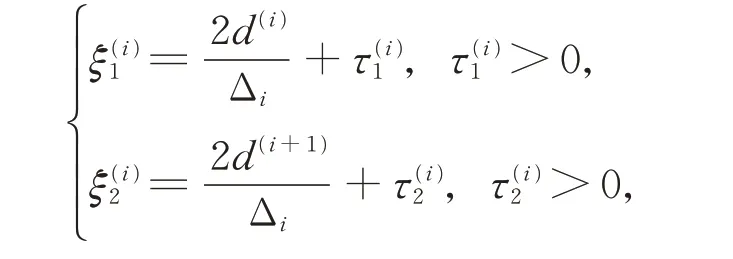
可得S′(x)≥0(x∈[x1,xn])。
2 可展曲面构造
由3D 射影空间中点与平面的对偶性,将式(3)中的控制顶点Pi(i=0,1,2,3)替代为控制平面Qi(i=0,1,2,3),便可得到带2 个形状参数的单参数平面族

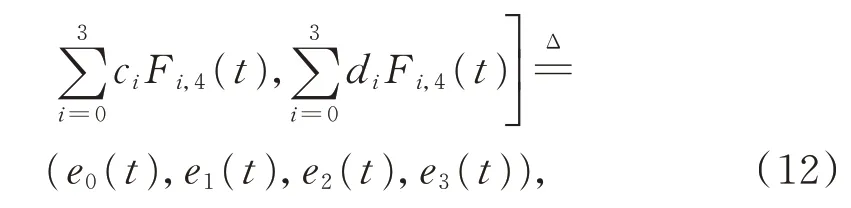
其 中,t∈[0,1],Qi=(ai,bi,ci,di),ai,bi,ci,di∈R(i=0,1,2,3)为控制平面,ai,bi,ci为控制平面上的点,di为(ai,bi,ci)到原点的距离。
2.1 包络可展曲面构造
在式(12)定义的带2 个形状参数的单参数平面族中,2 个相邻的平面相交于一条直线,且该直线位于包络可展曲面上。式(12)中,对应于任意一个t值的平面可表示为向量形式:
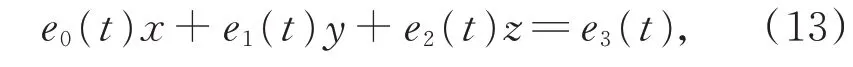
记为E(t)X=e3(t),其中,

对式(13)求一阶导数,得

记为E′(t)X=e′3(t),其中,

则式(13)和式(14)所形成的2 个平面的交线即曲面与t的母线,在可展曲面上,计算该交线L(t)=(u,v),其中,u=E(t)×E′(t)为L(t)的法向量,v=e′(t)E(t)−e(t)E′(t)。设p(t)为直线上与t最接近原点的点,则p(t)=。因而L(t)的方程可用以下参数形式表示:

2.2 脊线可展曲面构造
在式(12)定义的带2 个形状参数的单参数平面族中,3 个相邻平面的交点q(t)称为t的特征点,这些特征点形成的曲线,即为脊线。
对式(13)求二阶导数,得


则q(t)可表示为
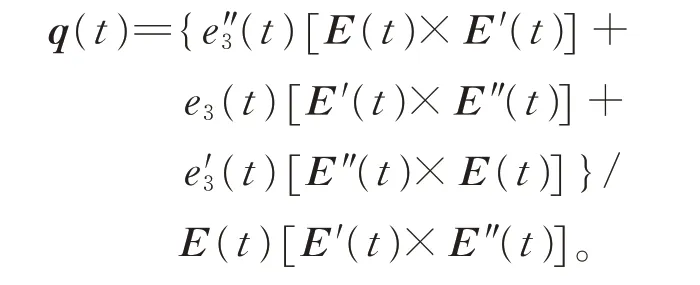
因此,可展曲面的参数表达式为

3 可展曲面的拼接连续性分析
假设待拼接的两可展曲面为

3.1 可展曲面的G0 连续拼接
若S(2)(0)=S(1)(1),则称两曲面G0连续。可得满足G0连续拼接的条件为

3.2 可展曲面的G1 连续拼接
其中,β1>0 为常数,则称两曲面G1连续。可得满足G1连续拼接的条件为

3.3 可展曲面的Farin-Boehm G2 连续拼接
若
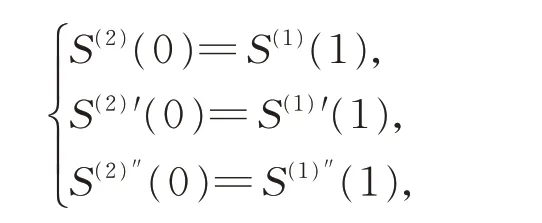
则称两曲面Farin-BoehmG2连续。当1≠0 时,可得满足Farin-BoehmG2连续拼接的条件为
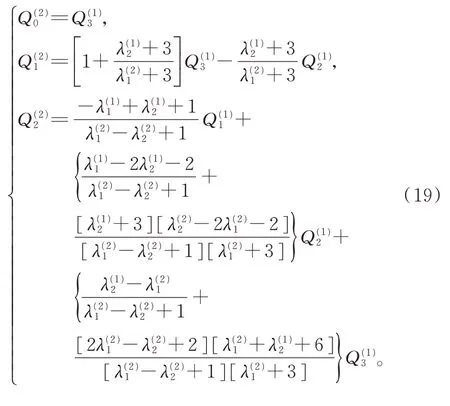
3.4 可展曲面的G2 beta 连续拼接
其中,β1>0,β2为常数,则称两曲面G2beta连续。当时,满足G2beta连续拼接的条件为

3.5 可展曲面的G3 beta 连续拼接
若

其中,β1>0,β2,β3为常数,则称两曲面G3beta 连续。当时,满足G3beta 连续拼接的条件如式(21)所示。
4 实例分析
4.1 形状参数
为更好地说明形状参数的调节作用,图2 给出了4 类曲线的几何造型实例。在图2(a)梨子、(b)蝴蝶中,实线、虚线、双划线所对应的参数值分别为λ1=λ2=0,0.5,1,随着λ1,λ2的增大,梨子、蝴蝶逐渐变大。在图2(c)花瓣、(d)枫叶中,实线、虚线、双划线所对应的参数值分别为λ1=0,λ2=1;λ1=0.5,λ2=0.5;λ1=1,λ2=0,随着λ1,λ2的变化,花瓣、枫叶的形状发生了变化。

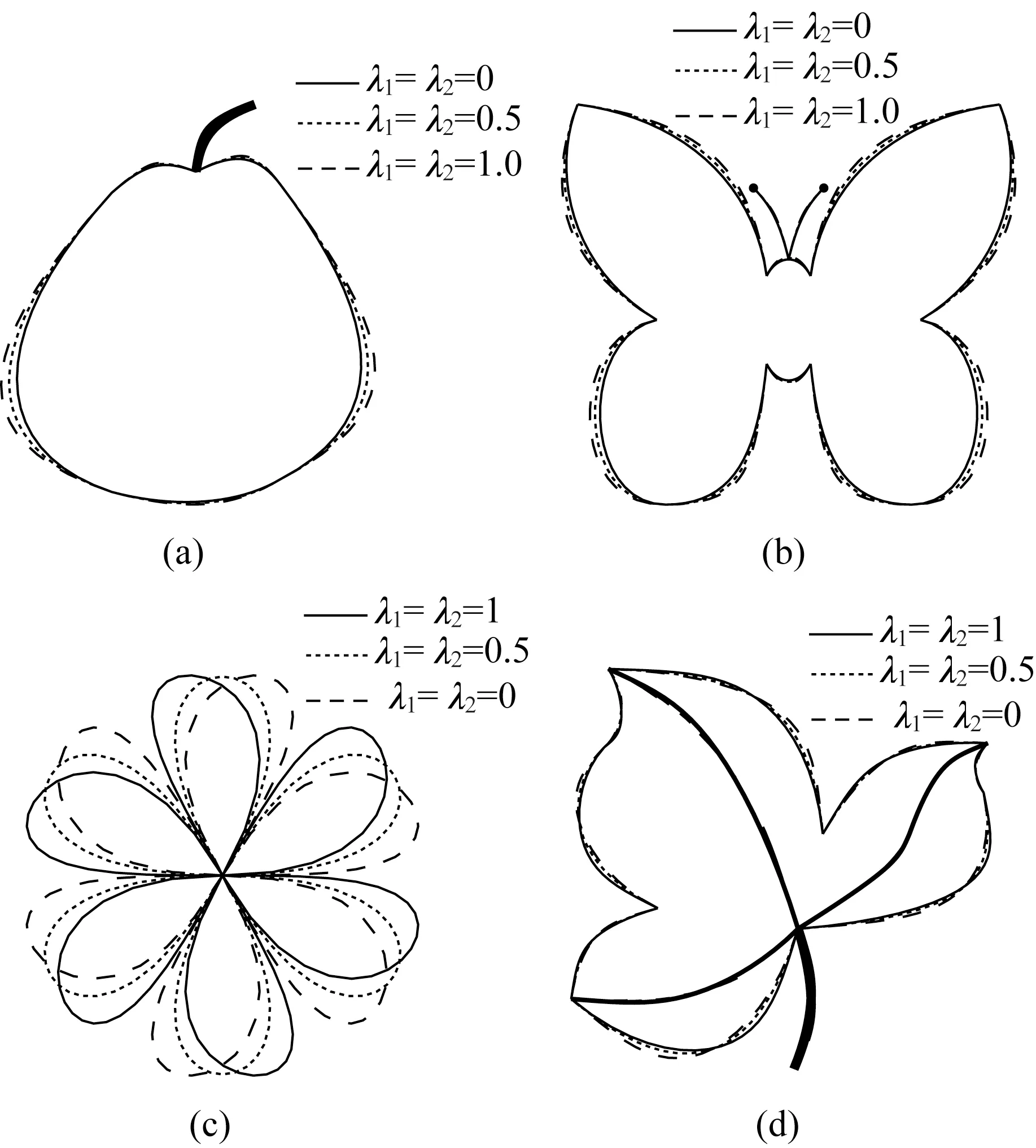
图2 曲线图形造型实例可视化Fig.2 Visualization of curve graphic modeling examples
4.2 插值样条的保正性
表1 所示为文献[12]中的正数据集。图3 为保正插值曲线可视化图,其中,图3(a)中,参数=1(i=1,2,…,6),ξ1=(3,15,1,1,20,10),ξ2=(3,2,1,1,4,5),(b)中,参数λ1=(0,0.9,0.5,0.2,0.8,1.0),λ2=(0,0.6,0.1,0.5,0.5,1.0),ε1=(3,1,3,3,3,8),ε2=(4,0,2,5,5,3)。表2 为文献[14]中的正数据集。图3(c)中,参数=1(i=1,2,…,7),ξ1=(3,1,1,1,1,1,1),ξ2= (3,1,1,1,1,4,1),(d)中,参数λ1=(0,1.0,0.5,0.2,0.8,1.0,0.5),ε1=(3,3.5,3,3,3,1,8),λ2= (0,1.0,0.1,0.5,0.5,1.0,0.8),ε2=(4,3,2,5,5,3,2)。(a)和(c)中的参数是随机选取的,曲线不保正。(b)和(d)中的参数满足式(7),曲线是保正的。
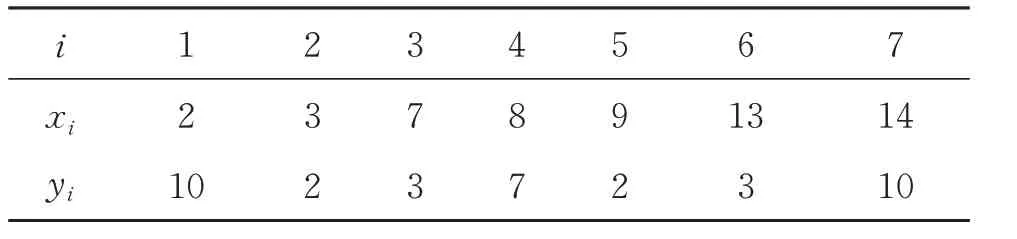
表1 文献[12]中的正数据集Table 1 Positive dataset in paper[12]
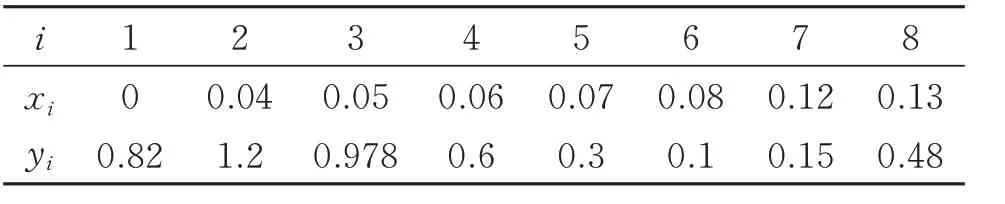
表2 文献[14]中的正数据集Table 2 Positive dataset in paper[14]
4.3 插值样条的保单调性
表3 为文献[12]中的单调递增数据集。图4 为单调递增插值曲线可视化图,其中,图4(a)中,参数=1(i=1,2,3),ξ2=(1,3,1),(b)中,参数λ1= (1,1,1),λ2= (0.1,1,1),τ1= (1,1,5),τ2=(5,1,1)。表4 为文献[14]中的单调递增数据集。图4(c)中,参数=1(i=1,2,…,10),ξ2=(1,3,1,1,1,1,1,1,1,1),(d)中,参数λ1=(1,1,1,1,1,1,1,1,0.2,1),τ1=(1,1,1,1,1,1,1,1,12,1),λ2=1(1,2,…,10),τ2=(1,1,1,1,1,1,1,1,5,1)。(a)和(c)中的参数是随机选取的,为非单调曲线。(b)和(d)中的参数满足式(9),为单调曲线。
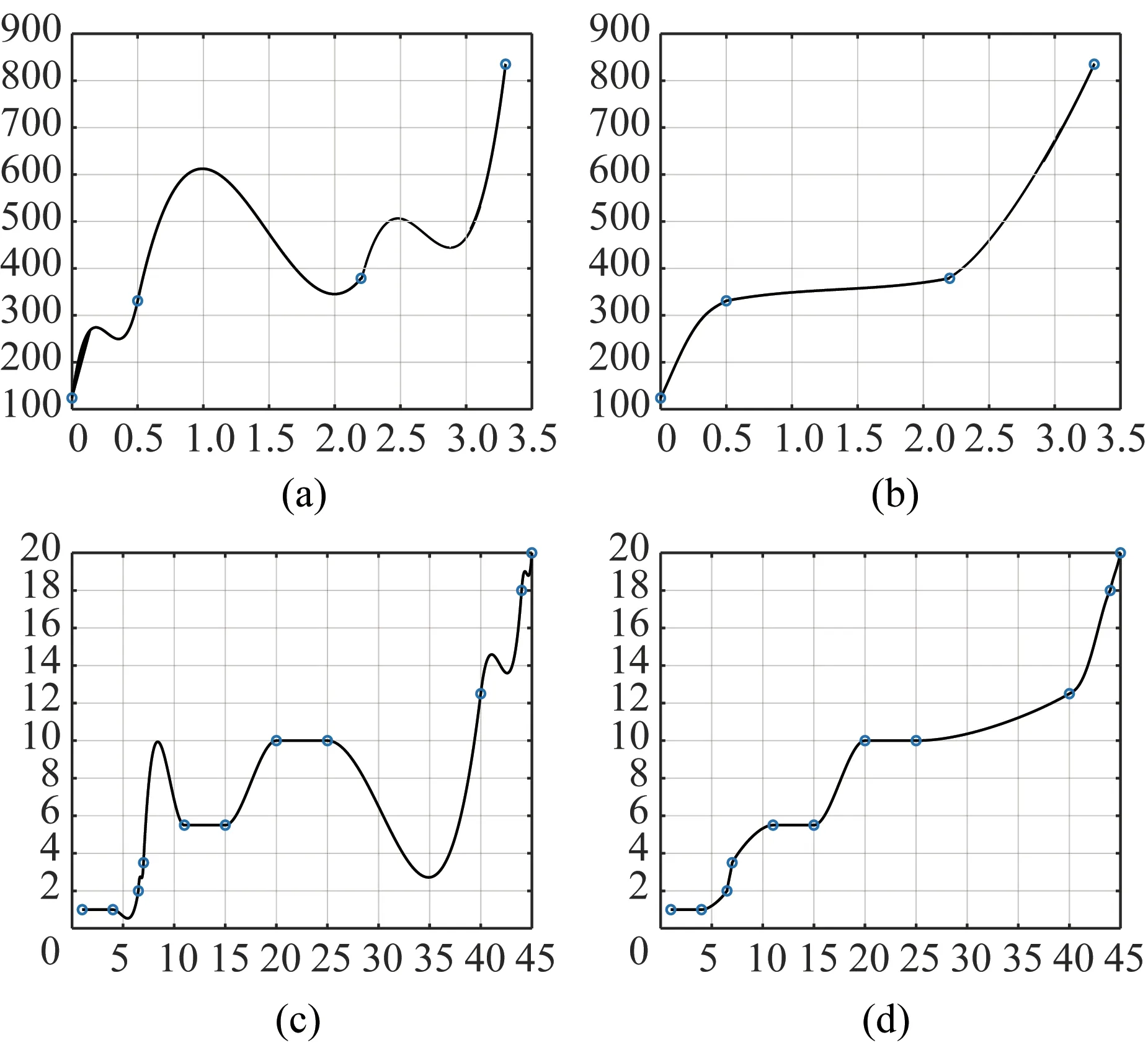
图4 单调递增插值曲线可视化Fig.4 Visualization of monotonically increasing interpolation curve
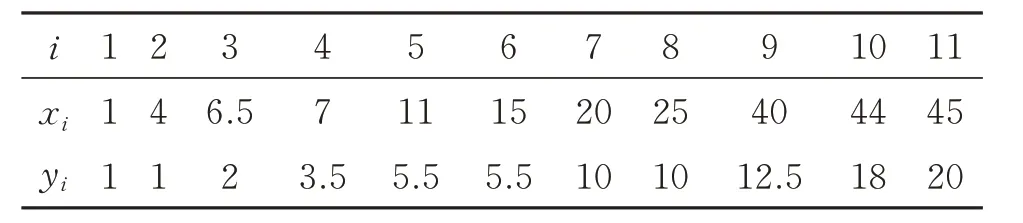
表4 文献[14]中的单调数据集Table 4 Monotonically increasing dataset in paper[14]
4.4 包络可展曲面
由文献[20]中4 个控制平面

所设计的包络可展曲面如图5~图7 所示。由图5可知,当λ2不变时,随λ1的增大,曲面的起始边(t=0)不断变长,终止边(t=1)的卷曲程度不断增加。由图6 可知,当λ1不变时,随λ2的增大,曲面的起始边(t=0)的卷曲程度不断增加,终止边(t=1)不断变长。由图7 可知,当λ1和λ2同时增大时,曲面的起始边和终止边均不断变长,弯曲程度有所增加。

图5 λ1 对包络可展曲面的影响可视化Fig.5 Visualization of the influence of λ1 on the enveloping developable surface

图6 λ2 对包络可展曲面的影响可视化Fig.6 Visualization of the influence of λ2 on the enveloping developable surface
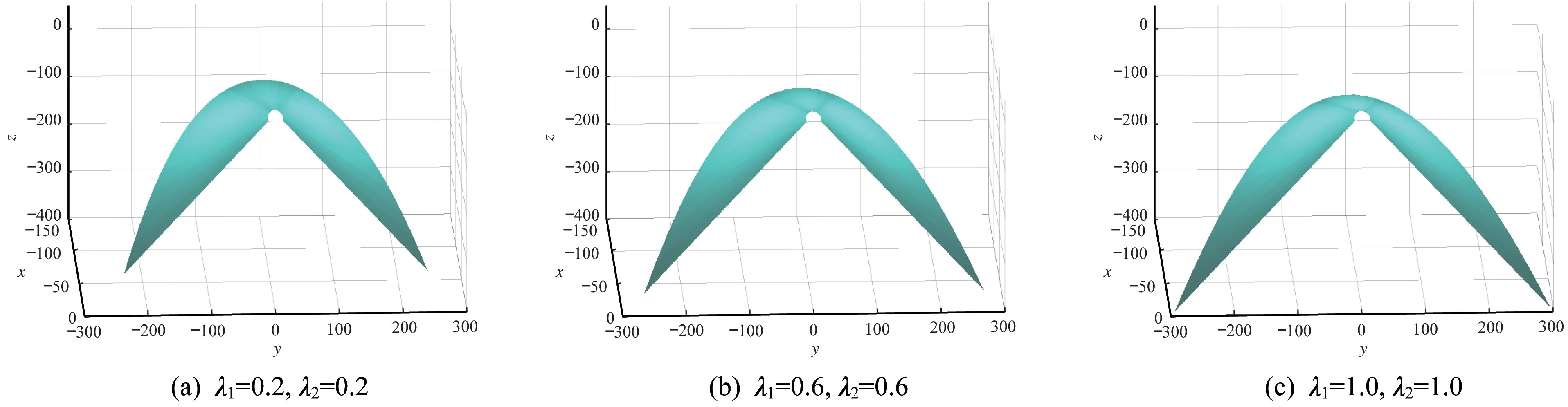
图7 λ1,λ2 对包络可展曲面的影响可视化Fig.7 Visualization of the influence of λ1,λ2 on the enveloping developable surface
4.5 脊线可展曲面
由文献[20]中4 个控制平面

所设计的脊线可展曲面如图8~图10 所示。由图8可知,当λ2不变时,随λ1的增大,曲面的起始边(t=0)不断变短,终止边(t=1)的卷曲程度不断增大。由图9 可知,当λ1不变时,随λ2的增大,曲面的起始边(t=0)的卷曲程度不断增加,终止边(t=1)不断变短。由图10 可知,当λ1和λ2同时增大时,曲面的起始边和终止边都不断变长,弯曲程度有所增加。
4.6 可展曲面的连续性拼接
由文献[20]中4 个控制平面

作为以下连续性例子的第1 个包络可展曲面的控制平面。由式(18)得到第2 个可展曲面的前2 个控制平面,任给后2 个控制平面即可达到G1连续。取β1=1,=0,设第2 个可展曲面的控制平面为

由式(19)、式(20)可得,第2 个可展曲面的前3个控制平面,任给最后一个控制平面,即达到Farin-BoehmG2连 续、G2beta 连续,由式(21)可得,第2 个可展曲面的所有控制平面达到G3beta 连续。连续性条件的参数设置、第2 个可展曲面的控制平面设置如表5 所示,拼接可展曲面可视化及相应的拼接曲面连续性高光带渲染结果如图12 所示,其中天蓝色曲面为第1 个可展曲面,米黄色曲面为第2 个可展曲面,紫红色为高光带。
5 结论及展望

图8 λ1 对脊线可展曲面的影响可视化Fig.8 Visualization of the influence of λ1 on the spine curve developable surface
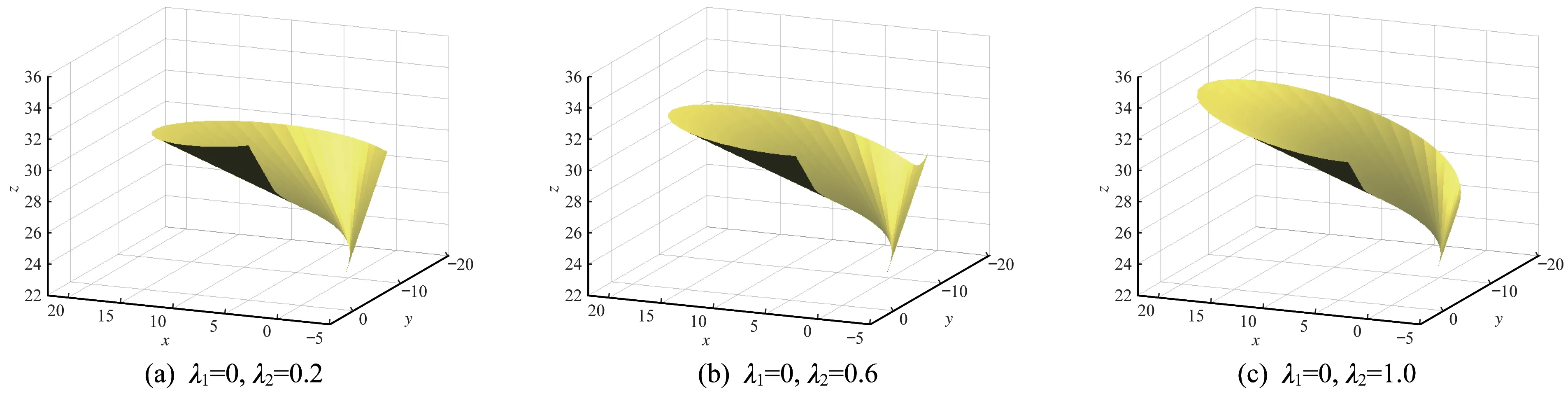
图9 λ2 对脊线可展曲面的影响可视化Fig.9 Visualization of the influence of λ2 on the spine curve developable surface
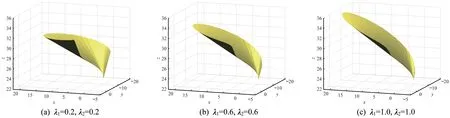
图10 λ1,λ2 对脊线可展曲面的影响可视化Fig.10 Visualization of the influence of λ1,λ2 on the spine curve developable surface

图11 不同参数对拼接G1 连续可展曲面的影响可视化及拼接曲面连续性高光带渲染结果Fig.11 Visualization of the effects of different parameters on the blending G1 continuous developable surfaces and rendering results of continuum highlight bands for blending surfaces
构造了带2 个形状参数的四次多项式基函数,是对三次伯恩斯坦基函数的扩展,具有退化性、非负性、归一性、端点性、对称性、线性无关性等性质。当该基函数用于构造曲线时,同样具有端点性、对称性、凸包性、变差减少性、平移与仿射不变性、形状可调性等性质,可在不改变曲线控制顶点的前提下,通过改变形状参数调节曲线形状。在此基础上,基于该基函数设计了4 次插值样条,该插值样条自动满足G1连续。并讨论了当形状参数及局部参数满足一定条件时,该插值样条具有保正性和保单调性。此外,将该基函数用于构造可展曲面,利用对偶性理论设计脊线可展曲面和包络可展曲面,并讨论了包括G0连续、G1连续、Farin-BoehmG2连续、G2beta连续、G3beta 连续的可展曲面的连续性条件。最后通过具体实例进行了验证分析。

表5 连续性条件的参数及第2 个可展曲面的控制平面设置Table 5 Parameter setting,control planes setting of the second developable surface of continuity condition

图12 拼接可展曲面可视化及拼接曲面连续性高光带渲染结果Fig.12 Visualization of the blending developable surfaces and rendering results of continuum highlight bands for blending surfaces
在设计可展曲面过程中,笔者发现控制平面的构造比较困难,其几何意义不够明确。如果能进一步探明可展曲面与其控制平面之间的几何关系,探寻控制平面的构造规律,将极大扩展可展曲面的应用范围。所有这些有待进一步研究。

