尖晶石氧化物能量和结构的第一性原理计算和机器学习

李一航 肖 斌 唐宇超 刘 馥 王小梦 刘 轶

(1.上海大学理学院， 上海 200444; 2.上海大学材料基因组工程研究院， 上海 200444)

高通量第一性原理计算方法[1-2]可用于系统研究大量的材料体系和构型， 但庞大的计算量使其成本高、耗时长.机器学习(machine learning， ML)方法[3-4]可以从计算或实验材料数据中进行数据挖掘或机器学习， 获得其中隐含的关联规律， 并用于对未知材料性能的高效预测.本研究基于高通量第一性原理计算数据构建机器学习模型， 可加快新材料的能量和结构预测，指导新材料的实验合成.

尖晶石材料因其庞大的种类、灵活可调的组分以及优异的物理化学性质而被广泛应用于锂电池正极[5-6]、光催化剂材料[7-8]、铁氧体磁性材料[9]和半金属材料[10]等领域.尖晶石氧化物可分为正尖晶石结构、反尖晶石结构和混合尖晶石结构[11-13].本研究中的正尖晶石氧化物化学通式为AB2O4， 空间群为Fdm， 其中A， B 阳离子[14]分别处于氧离子形成的四面体间隙(T 位点)和八面体间隙(O 位点)中.通过多种方式， 结合T/O 位点中心原子TC/OC和T/O 位点环境原子TE/OE特征构建的中心-环境(center-environment， CE)特征模型， 如图1 所示.本研究用73 种元素(见图2)分别替换尖晶石氧化物AB2O4结构的T 位点和O 位点原子， 获得了5 329(732=5 329)个可能的尖晶石氧化物.图2 中的灰色背景元素表示没有研究， 色标从蓝色到粉色作为对应的单原子基态总能量的函数， 正方形和圆形代表机器学习预测为“好”的T 位点和O 位点的稳定性元素.

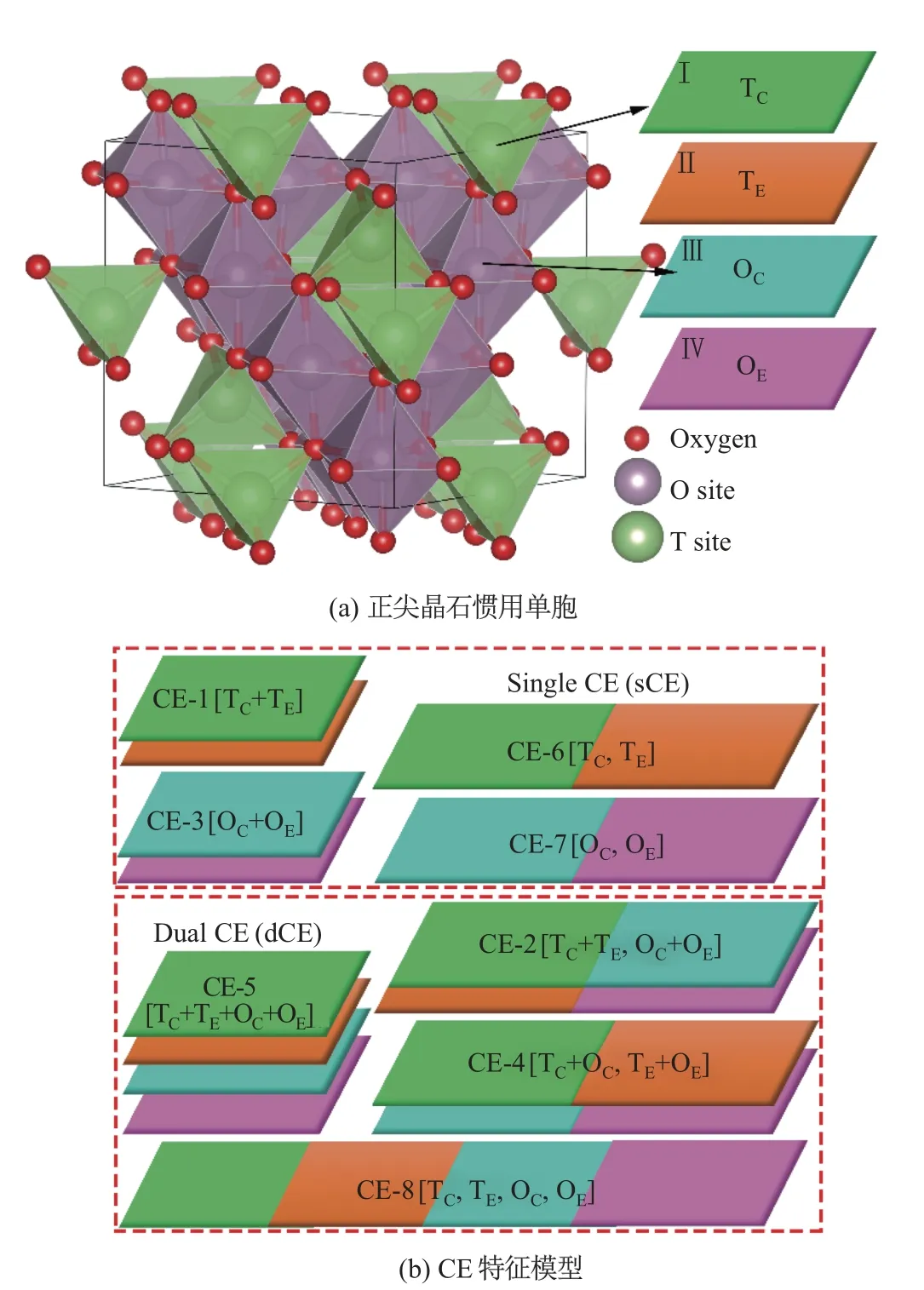
图1 正尖晶石惯用单胞和CE 特征模型Fig.1 Conventional cell of the normal spinel type and the CE feature models

图2 正尖晶石氧化物AB2O4 的组成元素Fig.2 Constitution elements of the normal spinel oxides AB2O4

在计算设计预测新材料时， 要求新材料必须是热力学稳定或亚稳定的， 而形成能[15-16]的大小是评估新材料是否热力学稳定的重要判据之一.为了得到准确的能量， 需要对预测结构进行充分弛豫， 弛豫后的计算结构可作为未来实验验证结构的理论参考依据.本研究使用高通量第一性原理计算方法研究了5 329 个尖晶石氧化物AB2O4结构的形成能和晶格常数， 提出了一种“中心-环境”(CE)特征模型， 以构建同时包含成分和结构信息的特征， 作为机器学习算法的输入变量.基于密度泛函理论(density functional theory， DFT)计算数据， 使用随机森林算法开发了机器学习模型， 对尖晶石氧化物结构的DFT 计算数据进行了学习训练， 获得的机器学习模型可以准确有效地预测尖晶石氧化物的形成能和晶格常数.

1 研究方法

1.1 第一性原理计算

本研究采用基于赝势投影缀加波的第一性原理计算方法， 通过VASP(Vienna Abinitio Simulation Package)软件包[17]进行计算.交换关联泛函选取广义梯度近似-PBE(generalized gradient approximation proposed by Perdew， Burke and Ernzerhof， GGA-PBE)， 平面波截断能为520 eV， 结构优化过程中保持能量的收敛精度为1×10-5eV/atom， 力的收敛精度为0.02 eV/°A(1°A=0.1 nm).通过收敛性测试， 布里渊区采用Monkhorst-Pack 的7×7×7 网格.本研究中尖晶石氧化物形成能的计算公式为

式中:Espinel是尖晶石晶胞的基态总能量;ET，EO和EO2分别为单个T 位点原子、单个O 位点原子和氧分子的基态总能量;nT，nO和NO分别为晶胞中T 位点原子、O 位点原子和氧原子的数量;N为单胞中的总原子数.

1.2 CE 特征模型

本研究结合元素/单质的基本性质和尖晶石氧化物的组成与结构信息来构造复合特征.每个构成元素选取了元素和相应单质的55 个基本性质[18]， 如原子半径、氧化态、电负性等(见表1).

表1 元素和单质的基本性质Table 1 Fundamental features of elements and simple substances

基于特征工程理念， 本研究构造了CE 特征模型， 通过将基本属性投影到由组分和结构信息组成的基组上来构造特征.定义一个由中心原子和周围环境原子组成的CE 原子集， 其中环境原子包括距离中心原子第1 近邻到第N近邻的原子(N=1～10).如果只有一个中心原子及其对应的环境原子， 则称之为单中心CE(single CE， sCE)特征模型; 如果包括两个中心原子及其对应的环境原子， 则称之为双中心CE(dual CE， dCE)特征模型.

CE 特征模型的基本思想是分别定义区分中心原子和环境原子， 然后将环境原子的基础性质以与中心原子距离的倒数作为权重进行线性加和， 从而实现将化学成分和结构信息编码到机器学习特征中.机器学习训练集D包括特征Fi(i=1～55 为性质序数)和预测目标T， 具体定义为

特征Fi(i=1～55)包括中心原子特征fC，i和环境原子特征fE，i， 即

中心原子的基本性质pC，i可直接作为该中心原子的特征， 即

环境原子的特征是根据每个环境原子j的基本性质pj，i及其到中心原子距离的倒数， 加权求和而成的复合属性特征， 即

式中，ωj为求和权重， 设环境原子j与中心原子的距离为rj， 则

本研究以单中心和双中心、标量和矢量等不同方式将中心原子和环境原子特征组合，构建成多种复合CE 特征模型.dCE 特征模型分别选取尖晶石氧化物结构的非等效T 位点和O 位点作为中心.TC和TE代表T 位点的中心原子及其周围环境， 如图1(a)中Ⅰ和Ⅱ所示; OC和OE代表O 位点的中心原子及其周围环境， 如图1(a)中Ⅲ和Ⅳ所示.CE-1， CE-3， CE-6 和CE-7 为4 个sCE 特征模型; CE-2， CE-4， CE-5 和CE-8 为4 个dCE 特征模型.在这8 个特征模型中， 分别将T 位点或O 位点定义为中心原子， 并将其第1 近邻至第10 近邻的原子分别考虑为环境原子.弛豫后的原型镁铝尖晶石MgAl2O4几何构型信息， 被用作构建本研究的尖晶石氧化物结构CE 特征模型时的基础结构.使用固定的原型结构信息来构造CE 特征氧化物， 可使机器学习模型更易于预测和迁移， 不受个别结构弛豫后几何构型变化的影响， 从而避免对新未知结构进行昂贵的第一性原理计算.

1.3 机器学习预测形成能和晶格常数

本研究采用随机森林算法训练机器学习模型.采用前述的CE 特征模型作为机器学习模型的输入变量， 预测性能包括尖晶石氧化物结构的形成能和晶格常数等.选取所有数据的80%作为训练集， 采用5 折交叉验证， 通过网格搜索确定最佳超参数.剩余的20%数据作为完全独立的性能测试集， 并不参与模型训练.将决定系数(coefficient of determination)R2、平均绝对误差(mean absolute error， MAE)和均方根误差(root mean squared error， RMSE)作为机器学习模型性能的评价指标， 具体定义分别如下:

式中:yi是实验或计算获得的目标值;是单个样本yi的预测值;是所有样本的预测值的平均值.

2 结果与讨论

2.1 不同CE 特征模型的预测结果

本研究构建了8 个基于不同组合方式的CE 机器学习特征模型， 其中包括4 个sCE 特征模型(CE-1， CE-3， CE-6， CE-7)和4 个dCE 特征模型(CE-2， CE-4， CE-5， CE-8).这些CE 特征模型对形成能预测的相关系数R2和RMSE 如表2 所示， 其中环境原子选取从中心原子的第1 近邻到第10 近邻的原子， 收敛结果以粗体显示.

表2 8 种CE 特征模型预测的形成能测试集的相关系数R2 和RMSETable 2 Correlation coefficient R2 and RMSE of the predictions of formation energies in the testing data sets by the eight CE feature models

通过对4 个sCE 特征模型的预测性能进行比较发现: ①标量特征模型CE-1[TC+TE]预测的RMSE 在第2 近邻处收敛于0.252 eV/atom， 而CE-3[OC+OE]预测的RMSE 在第4 近邻处收敛于0.166 eV/atom， 这表明T 位点标量特征模型的收敛速度比O 位点标量特征模型快， 但是后者的预测精度较高; ②二维矢量特征模型CE-6[TC， TE]预测的RMSE 收敛于第2 近邻， 而CE-7[OC， OE]预测的RMSE 在第4 近邻处收敛， 二者预测的RMSE 均约为0.145 eV/atom.可见， T 位点矢量特征模型的收敛速度仍然比O 位点矢量特征模型快， 但二者达到了相似的精度，且均优于标量特征模型.综合考虑收敛性和准确性， CE-6 是最佳的sCE 特征模型.

通过对4 个dCE 特征模型的预测性能进行比较发现: ①标量特征模型CE-5[TC+TE+OC+OE]预测的RMSE 在第2 近邻处收敛于0.164 eV/atom; ②矢量特征模型CE-2， CE-4 和CE-8 预测的RMSE 均收敛于约0.145 eV/atom， 优于标量特征模型.二维矢量特征模型CE-2[TC+TE， OC+OE]预测的RMSE 收敛于第1 近邻， 而CE-4[TC+OC， TE+OE]预测的RMSE 收敛于第2 近邻.这表明将中心原子与环境原子分离的收敛速度快于将T 位点原子与O 位点原子分离的速度.四维矢量特征模型CE-8[TC， TE， OC， OE]预测的RMSE 收敛于第1 近邻， 类似于CE-2[TC+TE， OC+OE].因此， 根据收敛性和准确性结果， CE-2[TC+TE，OC+OE]和CE-8[TC， TE， OC， OE]在所有8 个CE 特征模型中具有相似的最佳性能.此外， 四维矢量特征模型CE-8[TC， TE， OC， OE]同时区分了中心原子、环境原子以及T 位点、O 位点，其优点是可以避免因交换T 位点和O 位点异种元素而产生的特征简并， 但在二维矢量特征模型CE-2[TC+TE， OC+OE]中则会出现这种特征简并情况.

本研究中的四维和二维矢量CE 特征模型具有相似的预测精度.这可能是因为: 一方面很多T 位点和O 位点占据元素的稳定性， 具有近似交换不变的对称性; 如果这种位点占据稳定性的交换对称被破坏， 则四维矢量特征模型应该比二维矢量特征模型具有更准确的描述能力和预测准确性; 另一方面， 如果训练数据数量有限， 比二维矢量特征模型更复杂的四维矢量特征模型可能更容易导致过拟合.因此， 在CE 特征模型的实际应用中应根据研究结构的复杂性与可用数据集的大小折衷选择矢量特征模型的维数.如果结构复杂并且数据集很大， 高维CE 特征模型在准确性和可迁移性方面的表现会更好; 反之， 低维CE 特征模型就能达到足够高的预测精度， 且避免了过拟合.

所有8 种CE 特征模型对晶格常数预测的收敛行为类似于形成能， 结果如表3 所示， 其中环境原子选取从中心原子的第1 近邻到第10 近邻的原子， 收敛结果以粗体显示.但是， 对于晶格常数大于0.7 nm 的结构的预测精度不如其他结构.这可能是由于晶格常数大于0.7 nm 的结构数量较少， 从而导致机器学习模型不能对这类结构进行很好的学习.综合考虑预测精度和收敛速度， CE-8 特征模型预测的RMSE 在第1 近邻处达到了0.087°A， 表现最佳.

表3 8 种CE 特征模型预测的晶格常数测试集的相关系数R2 和RMSETable 3 Correlation coefficient R2 and RMSE of the prediction of lattice constants in the testing data sets by the eight CE feature models

2.2 预测结果的统计直方图

综合考虑晶格常数预测结果的精度和收敛速度， CE-8 特征模型在最近邻处的预测结果最好.图3 和4 是对5 329 种尖晶石氧化物结构形成能和晶格常数的DFT 计算结果的统计分析.5 329 种尖晶石氧化物结构中有141 种是已被实验合成的结构[19].图5 是CE-8 特征模型在最近邻处机器学习预测结果的统计， 其中141 个已知实验结构的形成能以红色表示.本研究对这些实验结构进行了DFT 计算， 发现其形成能在-2.999～-0.633 eV/atom 之间， 因此可将研究的尖晶石氧化物结构分为3 类: ①形成能大于-2.999 eV/atom 的更稳定(more stable，MS)结构; ②形成能介于-2.999～-0.633 eV/atom 之间的稳定(stable， S)结构; ③形成能小于-0.633 eV/atom 的较不稳定(less stable， LS)结构.如图5(a)所示， 本研究中的尖晶石氧化物结构可划分成361 个MS 结构、4 347 个S 结构和466 个LS 结构.此外， 还有155 个结构几何弛豫不收敛， 主要是含有活性金属Cs 和重稀土元素， 如Eu， Dy， Er 等.

图3 8 种CE 特征模型预测的形成能与DFT 计算结果的比较Fig.3 Comparisons of the formation energies between the DFT calculations and the predictions of the eight CE feature models

形成能可衡量物质的结合强度， 能作为判断物质是否热力学稳定的重要判据之一.本研究通过DFT 计算预测得到了形成能最大、热力学最稳定的前20 个尖晶石氧化物， 按热力学稳定性降低顺序分别是YbLu2O4，YbTm2O4，YbEr2O4，YbSc2O4，CaLu2O4，YbHo2O4，YbY2O4，CaTm2O4， YbDy2O4， SrLu2O4， CaEr2O4， YbTb2O4， HfYb2O4， CaHo2O4， SrTm2O4，ThYb2O4， CaSc2O4， EuHo2O4， YbGd2O4和CaY2O4.这些通过DFT 计算预测得到的最稳定的尖晶石氧化物结构的形成能范围是-3.57～-3.38 eV/atom， 远大于本研究实验结构的形成能范围(-2.999～-0.633 eV/atom)， 所以这些预测得到的稳定尖晶石氧化物结构更有可能被实验合成.本研究的预测结果为将来实验合成新型的、稳定的尖晶石氧化物结构指明了方向.

本研究预测的尖晶石氧化物的晶格常数(见图5(b))也呈正态分布， 绝大多数结构的晶格常数处于0.6～0.7 nm 之间.

图5 CE-8 特征模型预测的形成能和晶格常数的统计分布直方图Fig.5 Statistical distribution histogram of the formation energies and lattice constants predicted by CE-8 feature model

2.3 机器学习预测的形成能和晶格常数热图

机器学习预测的形成能分布如图6 所示， 其中横轴和纵轴分别按照T 位点和O 位点组成元素的原子序数排序.根据形成能范围定义的MS， S 和LS 结构在热图中分别大致对应蓝色、绿色和橘红色区域(白色区域是计算不收敛结构).这3 种区域呈现出局部聚集的块状， 而非稀疏的点样分布， 表明具有相近原子序数的结构元素通常形成具有相似稳定性的尖晶石氧化物.此外， 除少数情况外， 大多数聚集的块状呈对角对称分布.这表明将T 位点或O 位点元素替换为邻近的元素可以形成稳定性相似的结构， 即稳定性的位点互换不变对称性.这也解释了为什么会存在很多稳定的反尖晶石和混合尖晶石氧化物.

图4 8 种CE 特征模型预测的晶格常数与DFT 计算结果的比较Fig.4 Comparisons of the lattice constants between the DFT calculations and the predictions of the eight CE feature models

为便于指导实验合成新型稳定的尖晶石氧化物， 本研究分别针对T 位点和O 位点将73 个置换元素定性地划分为与稳定性有关的“好”和“坏”元素(见图2).如图6 所示: T 位点和O 位点的稳定性“好”元素组合可形成更稳定的MS 结构， 显示为图6 中的蓝色区域; T 位点和O 位点的稳定性“坏”元素组合形成了更不稳定的LS 结构， 显示为图6 中的橘红色区域; 如果在T 位点和O 位点分别存在稳定性“好”元素和“坏”元素， 则形成一般稳定的S 结构， 显示为图6 中的绿色区域，其稳定性与已知的实验结构相当.稳定性“好”和“坏”元素都呈现出T/O 位点的对称稳定性， 即大多数元素对于T 位点和O 位点同时都是稳定性“好”元素或“坏”元素(见图2 和6).但也有一些少数例外: 例如， Ru 是T 位点的稳定性“好”元素， 但却是O 位点的稳定性“坏”元素; Sc， Hf， Pa， U 和Np 是O 位点的稳定性“好”元素， 但却是T 位点的稳定性“坏”元素.

图6 机器学习预测的形成能热图Fig.6 Heat map of the formation energies predicted by ML

根据A， B 阳离子的平均离子半径， 对预测的尖晶石晶格常数进行约化， 即将晶格常数除以(RA+RB)/2， 其中RA和RB分别表示A， B 阳离子的离子半径.图7 为根据A， B 阳离子的平均离子半径约化后的晶格常数热图.可以看到: 约化后的晶格常数热图显示出分块分布的特性， 即原子序数相近的元素形成的尖晶石氧化物结构具有近似的约化晶格常数; 约化后的晶格常数显示出沿对角线的对称性， 表明将T 位点或O 位点元素替换为邻近的元素可以具有相近的约化晶格常数的结构.相比于同周期的其他元素， 含碱金属元素Li， Na， K， Rb， Cs 的尖晶石结构通常具有相对较小的约化晶格常数.这可能是由于碱金属元素相比同周期元素拥有更大的离子半径.此外， 当A， B 阳离子的原子序数均较小时， 其晶体结构比原子序数均较大时具有明显更大的约化晶格常数.这可能是由于原子序数均较小时的元素具有较小的电负性， 更容易向氧转移电子， 从而导致带更多负电的氧离子间排斥力增加， 约化晶格常数增加.

图7 根据A， B 阳离子的平均离子半径约化后的晶格常数热图Fig.7 Heat map of the lattice constants after reduction of the average ion radius of A and B cations

2.4 计算和机器学习预测结果与已被实验合成的尖晶石氧化物的性质比较

为了进一步独立测试验证本研究结果的准确性， 将文献报道的已被实验合成的141 个尖晶石氧化物结构的晶格常数实验值分别与DFT 计算值和随机森林机器学习预测值进行比较， 结果如图8 所示.可见， 机器学习预测点阵常数的RMSE 为0.04 °A， 比DFT 计算的RMSE(0.09 °A)更低， 进一步证实了机器学习模型的预测有效性.表4 和5 是部分已知尖晶石氧化物结构的形成能和带隙的实验值、DFT 计算值以及机器学习预测值.DFT 计算值与部分实验值的偏差可能来源于交换相关密度泛函的近似.由于将DFT 计算值作为目标值进行机器学习训练， 所以机器学习和DFT 计算结果比较一致.

表4 部分已知尖晶石氧化物结构的形成能的实验值、DFT 计算值和机器学习预测值Table 4 Experimental values， DFT calculation values， and ML prediction values of the formation energies of some known spinel oxides (eV·atom-1)

图8 已被实验合成的141 个尖晶石氧化物结构的晶格常数实验值与DFT 计算值和机器学习预测值的比较Fig.8 Comparisons of the experimental lattice constants of 141 known spinel oxide structures with the results calculated by DFT and predicted by ML

表5 部分已知尖晶石氧化物带隙的实验值、DFT 计算值和机器学习预测值Table 5 Experimental values， DFT calculation values， and ML prediction values of the band gap of some known spinel oxides eV

3 结束语

本研究通过第一性原理计算和机器学习方法， 系统研究了包含73 种A/B 构成元素的5 329 种AB2O4正尖晶石氧化物.根据141 个已知的尖晶石氧化物结构的形成能范围(-2.999～-0.633 eV/atom)， 将预测结构分为361 个更稳定(MS)结构、4 347 个稳定(S)结构和466 个较不稳定(LS)结构.为指导实验成分设计， 提出了与尖晶石氧化物的稳定性定性相关的“好”和“坏”的构成元素.常见的稳定性“好”元素是Ⅱ， Ⅲ， Ⅳ族元素和稀土元素， 大部分具有对称的占位稳定性.含IA 族碱金属元素的尖晶石氧化物结构通常具有较大的晶格常数.本研究预测的稳定性尖晶石氧化物结构对进一步实验合成新型尖晶石氧化物具有指导意义.

本研究构建了包含成分和结构信息的CE 机器学习特征模型.该模型能够高效预测尖晶石氧化物的能量和结构特性， 并获得与第一性原理方法相当的精度.通过考察不同的特征构建方式， 发现双中心CE(dCE)模型的预测性能通常优于单中心CE(sCE)模型， 并且应综合考虑结构的复杂性和可用数据的数量来选择复合特征向量的维数.如果结构复杂、对称性很低并且具有大量数据， dCE 或多中心CE 特征模型的矢量形式将比sCE 模型更加准确可靠.本研究中的CE 特征模型可推广用于其他凝聚态材料能量和结构的机器学习预测.