Thiele 型张量连分式插值及其在张量指数计算中的应用

蒋祥龙，

(上海大学理学院， 上海200444)

张量常微分方程的初值问题[1]可以表述为

式中，A和Y0是给定的常张量.该张量常微分方程的解为

式中， exp((t-t0)A)就是著名的张量指数函数.对于给定的常张量A， 张量指数一般表示为如下的级数表达式:

在文献[1]中， 式(3)被用来近似计算或者逼近张量指数， 即

式中， 截断的最高项nmax满足

本研究提出了一种张量广义逆Thiele 型连分式插值方法， 用来近似计算式(2)中的张量指数函数.该方法可以看作矩阵广义逆Thiele 型连分式插值方法[2–5]在张量上的推广， 且具有如下特点: ①在计算过程中，不必计算张量的乘积; ②该方法用连分式表示， 是一种递推计算方法.

1 有关张量的几个基本概念

张量是一个多维数组.一阶张量是一个向量， 一个二阶张量是一个矩阵， 并且是一阶张量.3 个或3 个以上的张量称为高阶张量.所谓张量矩阵化， 就是把张量用矩阵的形式展开[6].例如， 考虑一个三阶张量A= (ai1，i2，i3)∈R2×3×3.如果指定张量A的第3 个指标， 可以得到3 个2×3 矩阵， 由此该张量可以表示为

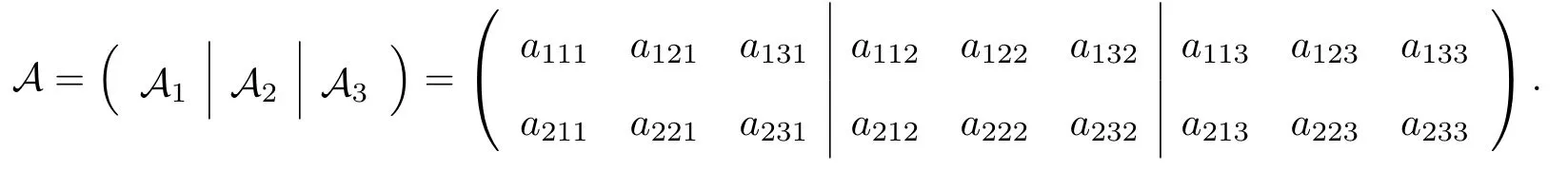
定义1 和定义2 为3 阶张量t乘积(t-product)的定义.该定义自然地以递归的方式推广到高阶张量.

定义1[7]设A ∈Rl×m×n.张量A的块循环矩阵为

定义张量的展开(unfold(·))[7]为

再定义张量的折叠(fold(·))[7]， 二者互为相反逆运算， 从而满足fold(unfold(A))=A.

定义2[7]设A和B分别是l×p×n和p×m×n张量.它们的3 阶张量乘积A*B是如下的l×m×n张量:

定义3 和定义4 为张量的内积和张量的范数， 可以看作是矩阵的直接推广.

定义3[8]设A=a(i1，i2，···，ip)∈Cn1×n2×···×np，B=b(i1，i2，···，ip)∈Cn1×n2×···×np.张量A和B的内积定义为

定义4[8]设A=a(i1，i2，···，ip)∈Cn1×n2×···×np， 它的范数定义为

根据式(5)和(6)， 不难证明

式中，A*表示张量A的共轭转置张量.

2 Thiele 型广义逆张量连分式插值

本研究首先给出基于式(7)的一种张量广义逆的定义， 然后在此基础上构造了Thiele 型张量连分式插值公式.这种张量广义逆可以看作相应的矩阵广义逆[2-5]在张量上的推广， 并已被成功应用于张量Pad´e 型逼近方法[9]、张量广义逆Pad´e 逼近的连分式方法[10]和APCILON方法[11].

定义5设张量A ∈Cn1×n2×···×np且A/=0， 张量范数‖A ‖2=A·A*由式(7)给出.张量A基于内积的广义逆定义为

或

式中， 广义逆表示张量A的倒数.

按照张量广义逆的计算公式(8)或(9)， 定义Thiele 型张量截断连分式如下: 设插值点的集合为Φ={xi， i=1，2，··· ，n， xi ∈R}.根据式(8)或(9)， 递推地构造第n个Thiele 型截断连分式为

式中，

根据表达式(10)和(11)， 给出如下的递推算法1.

算法1计算截断插值连分式(10).

步骤1 给定初始值(xi，Ai)，i=0，1，··· ，n.

步骤2 Forl=0，1，··· ，n.

步骤3 计算Bl(x0，x1，··· ，xl).

步骤4 如果Bl(x0，x1，··· ，xl)=0， 转步骤1.结束.

步骤5 结束.

步骤6 通过式(10)计算Rn(x).

定理1～定理3 分别为Thiele 型广义逆张量连分式插值公式(10)的存在性、整除性和特征性定理.考虑到它们的证明方法与相应的矩阵方法基本相同， 此处只给出有关结论.

定理1(存在性)[3]设Bl(x0，x1，··· ，xl)∈Cn1×n2×···×np[x]，0 ≤1 ≤n， 存在且不等于0(except forB0(x0)).同时，

满足

则式(10)中(x)存在， 并成立插值条件(xi)=Ri，xi ∈Φ.

定理2(整除性)[3]设Bl(x0，x1，··· ，xl)∈Cn1×n2×···×np[x]，0 ≤l≤n，xi ∈Φ.在式(10)中，从后逐次向前利用张量广义逆计算(xi)，则一个张量多项式P(x)∈Cn1×n2×···×np[x]和一个实多项式q(x)存在， 并且满足

式中，q(x)|‖P(x)‖2表示分母实多项式能够整除分子张量多项式的范数的平方.

定理3(特征性)[3]根据定理2， 设式(10)中截断连分式为(x) =P(x)/q(x)， 则成立: ①如果n是偶数，(x)具有阶数为[n/n]型; ②如果n是奇数，(x)具有阶数为[n/n-1]型， 其中[l/k]型表示分子张量多项式为l阶， 分母实多项式为k阶.

例1 设插值点x0=-1，x1= 0，x2= 1， 相应的待插值张量值Ai ∈C2×2×3，i= 0，1，2，则

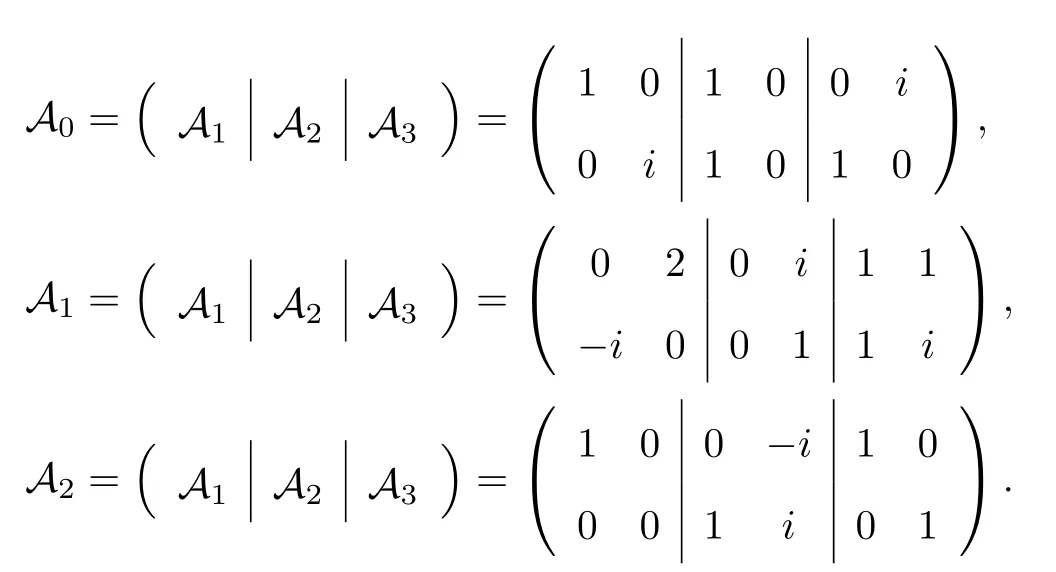
根据连分式插值公式(10)和(11)， 利用张量广义逆(8)或(9)分别得到

不难验证插值条件R2(xi)=A(xi)，i=0，1，2.

3 在张量指数函数计算中的应用

给定张量A和t0= 0， 本研究利用张量连分式插值公式(10)， 计算张量常微分方程的解(2)， 或者在如下解

中， 近似计算张量指数函数exp(At)的值.本研究计算exp(At)值的方法分为如下几个步骤:①利用张量的t乘积(见定义2)来计算张量A的幂; ②导出张量指数函数exp(At)的Tailor 展开式; ③选择合适的插值点， 例如， 考虑在原点附近选择张量A的特征值; ④计算相应的插值函数的值; ⑤根据算法1 得到连分式插值函数R(T)， 并利用其计算张量指数函数的值; ⑥考虑计算值是否满足误差要求， 具体步骤如算法2 所示.

算法2计算张量指数函数的值.

步骤1 利用张量的t乘积计算An， n=0，1，···， 从而得到exp(At)的Tailor 展开式.

步骤2 在t0=0 临近选择合适的插值点ti， i=0，1，··· ，n.

步骤3 计算待插值的值exp(Ati)， i=0，1，··· ，n.

步骤4 由算法1 得到连分式插值公式Rn(t).

步骤5 给定误差限ε， 计算误差Res(ti)=‖exp(Ati)-Rn(ti)‖.

步骤6 如果Res(t)≥ε， 转步骤2， 否则， 输出Rn(t).结束.

例2 在张量指数函数exp(At)中， 给定计算张量指数函数exp(At)在临近t0=0 的值.

步骤1 利用张量的t乘积计算An， n=0，1，···， 得到

步骤2 计算张量A的特征值[12]为0，1/3，1/2，5/6， 选择插值点为t0= 0， t1= 1/3， t2=1/2.

步骤3 计算待插值的张量指数函数exp(Ati)， i=0，1，2 的值为

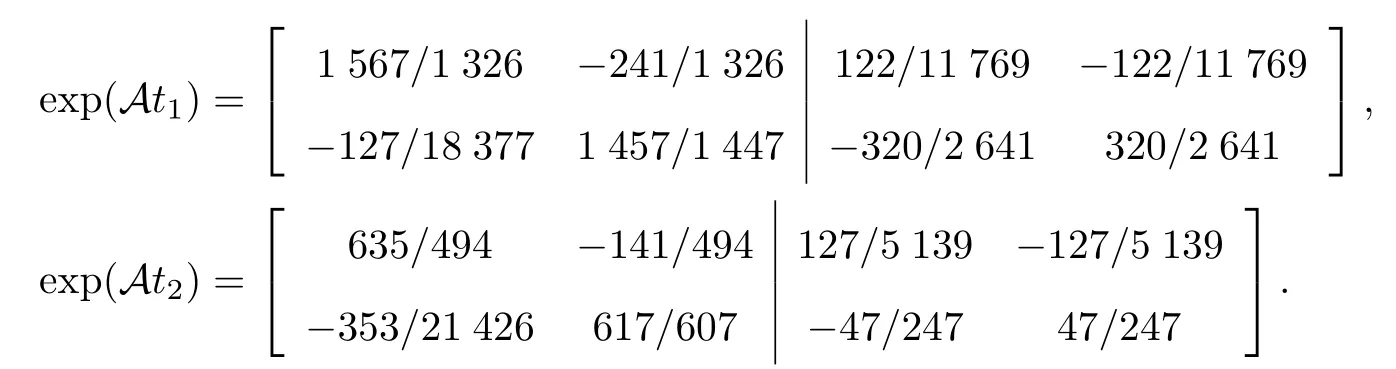
步骤4 根据步骤2 和步骤3， 由算法1 得到

于是得到连分式插值公式

式中:

步骤5 设误差限ε= 1×10-3， 计算误差Res(ti) =‖exp(Ati)-R2(ti)‖.这里， 取张量指数函数Tailor 展开式前15 项的和作为exp(At)的精确值.同时， 取连分式插值函数R2(t)计算的值作为exp(At)的近似值， 结果如表1 所示， 其中exp(At)的精确值与近似值分别用Evalue 和A-value 表示.

表1 R2(t)近似计算exp(At)的数值结果Table 1 Comparisons of numerical results of R2(t) for exp(At)

从表1 可以看出， 当插值点在0～0.6 之间时， 连分式插值函数R2(t)计算张量指数函数的值的时候， 逼近效果比较好， 特别当插值点t在0.3～0.5 之间时， 数值结果更加精确.