转化思想在初中数学解题教学中的运用研究

摘要：转化思想是解决初中数学题目的重要思想，利用转化思想可以把繁杂缠绕的数学题目变得简洁明了。初中阶段是学生智力以及逻辑思维能力发展的关键时期。数学教师在教学过程中要有意识地培养学生正确运用转化思想，从而使理论指导生活，强化数学核心素养，让学生善于通过已知内容解决未知的问题。

关键词：初中数学;转化思想;解题

初中阶段的数学知识难度有明显的提升，很多小学生升入初中之后短时间内很难适应，因此很多同学会产生畏难心理，就此产生对数学的负面情绪。初中教师要重视对学生转换思维的培养，帮助他们把相对繁杂的问题转为适合自己的解题思路，就能使学生在吸收知识的同时也能领悟到初中数学解题思想，帮助学生树立正确的学习信心，从容面对各种复杂的问题。

1转化思想在初中数学中的形式

转化思想是初中数学教学中的关键内容，包括类比、分解、等价、语言、间接、数形等不同的转化形式，通过灵活运用这些转化方式，帮助学生对数学知识融会贯通，增强学生的综合应用能力。

1.1类比的转化

类比的转化注重相似性，利用已掌握的知识点去探索新的相关知识点。例如在学习北师大版八年级上册二元一次方程组时，教师可以引导学生利用七年级所学的一元一次方程式的知识点进行类比学习，探究两者之间的相关点。

1.2数字与图形之间的转化

数字与图形之间的转化需要把握二者之间的逻辑关系，通过形式的转变简化思路，从而得出答案。分析题目的关键信息，通过函数或是方程式，组建相关图形。例如：根据已知的图象，求交点c。如果学生凭空想象很难正确理解交点的概念，而通过将图形转变为函数，建立两个方程组，通过计算的方式可以求解，从而快速对交点c定位，帮助学生理解交点的概念。

1.3语言的转化

语言的转化可以让题目变得浅显易懂，更方便学生思考。例如，教师在讲解“等腰三角形两底角相等”这个定理时，教师可以让学生动手制作等腰三角形，然后利用直尺、量角器等工具测量，发现无论边长怎样变换，两底角的度数基本相同。通过实践操作将枯燥的文字进行转化，既能够锻炼学生动手操作的能力，也可以强化学生对定理的理解，提高学生对数学知识的把握程度。

1.4等价的转化

等价的转化就是将不晓转化为知晓。初中数学题目相对来说比较难，各种条件都是未知的，需要学生根据已知条件进行转化，等价转化的思路就是通过相等的条件进行假设，从而判断原命题与逆否命题之间的关系。例如：在方程式计算的过程中，如果直接计算变量非常复杂，但是如果通过常量和变量相对性的特征，能够极大地简化计算过程，从而快速判断x2 - 2x + m - 3 = 0在[0，+∞）m的取值范围。

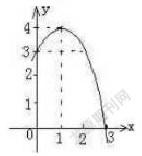
解：由原方程，得m = -x2 + 2x + 3 = -（x - 1）2 + 4， x∈ [0，+∞）

作出它的图象，如图，观察图象可知，

当 x ∈ [0，+∞）时，m∈ （-∞，4]，

并且m ∈ [3，4]时，每个m值对应着两个不同的x值。

故当m ∈[3，4]时，所求方程在[0， +∞）上有两个不相等的实数根。

1.5分解的转化

分解转化能够使复杂的大问题转换为若干个小问题，使学生对个个问题逐一击破，不仅难度明显下降，同时也可以引导学生逐步思考，形成循序渐进的逻辑观念。

2在初中数学解题教学中转化思想的应用

2.1把复杂问题转化为简单问题

初中学生的逻辑思维能力还不是很强，初中教师需要引导学生把相对复杂的问题简化成学生已经掌握的易懂知识。

例：解方程（xx-1）3-2（xx-1）+ 8=0

分析：此方程形式较复杂，可通过换元化为简单方程。

令xx-1=y，则y3-2y+8=0， 通过换元转化为会解的一元二次方程可进一步求解。

2.2通过生活问题解决数学难题

例题：在某超市销售的篮球每件为20元，每月銷售量y（件）与销售单价x（元）之间存在函数关系y=-10x+500。当超市每月获得利润为z（元），求超市如何定价才能确保利润最大化。这道题目与学生的生活十分接近，能够很好的激起学生参与兴趣，而且“利润最大化”的概念在生活中也有很多的用途，因此教师可以指导学生利用数学知识进行计算，每月利润=每件产品利润×销售产品件数，即z = （x-20）y=（x-20）（-10x+500）。通过抽象的概念转化为直观，根据计算可得x=35，因此每个篮球定价为35元时可以实现利润最大化。

结语

综上所述，转化思想是解决初中数学难题的有效方式，初中数学教师需要引导学生掌握转化思想的几种常见形式，提高学生思考的灵活性和变通能力，为今后更深入的数学学习打下良好的基础。

参考文献：

[1]杨苗苗.浅议转化思想在小学数学教学中的应用[J].考试周刊，2019，（59）：82.

[2]康小燕.转化思想在初中数学解题中的应用[J].名师在线，2016，（011）：51-52.

[3]李秀芹.转化思想在初中数学解题中的应用[J].科普童话，2018，000 （05X）：P.75-75.

[4]殷剑炜.转化思想在初中数学解题中的应用[J].新课程·中旬，2017，（10）：70.

作者简介：第一作者：刘建荣（1989.02—），女，汉族，云南曲靖市人，云南师范大学本科，篆角初级中学校一级教师，研究方向：数学教学