落实“三个理解”，实现“三会”目标

何胜鑫

【摘要】章建跃教授提出课堂教学要关注“三个理解”，即理解数学、理解学生、理解教学，旨在解决“教什么”“怎么教”“为什么这样教”的问题。在“三个理解”理论指导下的课堂教学，要求执教者追溯知识源头，重塑数学知识的产生过程，体现数学文明的探索历程，让学生感悟数学与现实世界的紧密联系。教师要努力做到知其然，知其所以然，知其所以必然，从而揭开数学神秘的面纱，激发学生学习的内驱力。

【关键词】三个理解;初中数学教学;现实世界

“三个理解”是有效进行课堂教学的根本保证，是教师专业化发展的基石。落实“三个理解”，要清楚数学知识从哪里来，到哪里去。数学教学是还原和重现数学知识的产生的过程，一切课堂教学行为都是为了知识的生长。史宁中教授说过：“数学学习的最终目标，是让学习者会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。数学的眼光就是抽象，数学的思维就是推理，数学的语言就是建模。”教师只有落实“三个理解”，才能实现“三会”目标。落实“三个理解”体现在课堂教学的每一个环节，比如创设情境导入新课环节，可以创设体现数学知识产生发展需要、数学与生活联系的情境，使学生感悟数学知识产生的必然性;设计学生活动开展研究环节，可以采取问题引导学习的方式，让学生带着问题开展探索活动，将学生学习方式的转变落在实处。要注重学生参与，让学生有主动学习的机会，教师可适时进行预设性提问，让学生的思维得到发展。当学生“心求通而未得，口欲言而未能”的时候，教师相机诱导，通过有目的性、针对性的追问方式，进行点拨指引，让学生“开其意”“达其辞”，从而推动学生理解数学。笔者有幸观摩了周海东老师执教的《5.2 图形的运动》一课，周老师教学设计的每一环节都很精致、精准、精深，真正落实了“三个理解”。下面笔者结合这节课，谈谈自己的学习感受与思考，不当之处敬请指正。

一、学会用数学的眼光观察世界

教学环节（一）观察与思考：

师：我们生活在一个运动的世界，自古以来，人们对运动充满了好奇，并不断探索，诗人用语言和韵律来赞美运动，写出了“大江东去，浪淘尽，千古风流人物”，你感受到了运动没有？画家用色彩和形态来描绘运动，你看到了什么？

生：奔腾的骏马。

师：用数学的眼光来观察世界，这些建筑可以看成几何体，那么图形的运动又是怎样的呢？我们一起研究图形的运动。

师：刚才看到的几何体有哪些基本元素？

生：有点，有线，有面。

师：我们想研究图形的运动，肯定要研究这些图形上最基本的元素的运动。

师：把笔尖看成一个点，请用最简单的数学语言把你看到的现象描述出来。

生：点动成线。

师：生活中有这样的例子吗？（生举例：汽车运动等）

师：（课件动态呈现雨刮器在汽车玻璃上运动的画面）你能描述自己看到的吗？

生：线动成面。

师：举一些生活中的例子？（生举例：打开扇子，拉动窗帘等）

师：将三角形绕一条边旋转一周，能形成什么呢？（操作演示：教师将三角形插在电钻上，启动电钻，使得三角形快速旋转）

师：那将长方形旋转，会形成什么图形呢？（继续用电钻操作演示）

师：这个现象归结为什么？

生：面动成体。（软件演示：教师用GGB软件演示三角形平移、旋转，让学生感受面动成体的过程）

师：点动成线，线动成面，面动成体，换句话来说，所有的几何体都可以看成由谁运动形成的？（软件演示：教师用几何画板演示点动成线，线动成面，面动成体，学生再次直观感知）

生：点。（课件展示：几何体都是可以看成由点运动而形成的）

思考：第一个环节的设计是想让学生“学会用数学的眼光观察世界”，体现抽象的过程，是自外而内的，基于学生生活经验，通过体现现实生活场景，学生充分感受到自己生活在运动的世界里，通过操作、观察，切身感受点动成线、线动成面、面动成体的运动过程。教学背景、素材、工具等都取自现实生活，知识生成的过程生动形象，富有趣味性，学生能够初步感知图形的旋转、平移、翻折等变换。七年级的学生正处于从形象思维向抽象思维过渡的阶段，教师借助GGB、几何画板软件将具体实例中点动成线、线动成面、面动成体的运动过程抽象成数学概念，展示给学生看，层层递进，最后学生能感悟到图形运动的本质是点的运动。教师通过以上一系列教学手段，推进学生对数学知识的深入理解，让学生感受图形的形成发展过程，教师也达到了教学的效果。教师用自己的实际教学过程诠释了“教什么”“怎么教”“为什么这样教”的问题。学生的学习体会是深刻的，能充分感受到数学知识来源于生活，生活中处处有数学，学会用数学的眼光来观察现实世界。

二、学会用数学的思维思考世界

教学环节（二）操作與感知：

师：两个完全相同的三角板，你能拼成不同的图形吗？小组合作，把拼成的图形画在任务单上。

师：图形有几种？

生1：4种。

生2：6种。

师：老师告诉你们肯定有6种，谁能解释一下？

生：只有两条边完全相同才能拼在一起。

师：拼的时候不再是无序地拼，怎么拼？（教师操作演示一条边的两种情况，其他两条边的情况，学生展示拼的方法，其他学生完善自己的图形）

师：黑板上拼成的图形能不能分分类呢？

生：用斜边拼的一类，用较长的直角边拼的一类，用较短的直角边拼的一类。

师：这样我们不拼也能知道是6种，用的是什么数学思想？就是分类讨论的思想。

师：从运动的角度思考，这6种图形怎么产生？（学生根据6种图形对应回答出翻折还是旋转等）

师：（课件展示）复杂图形由简单图形组合而成。

思考：第二个环节的设计是想让学生“学会用数学的思维思考世界”，体现推理的过程，即思维从无序走向有序。在此环节，教师给足学生动手操作的时间，让学生尝试将两个完全相同的三角板拼在一起。显然，学生的思维一开始是无序的，大部分学生在动手操作拼图的过程中都是杂乱无章的。在学生不断试错的过程中，教师引导学生思考满足怎样的条件才能使两个图形拼在一起。学生发现相等的边可以拼在一起，教师再乘机追问相等的边拼在一起可以有几种情况，让学生动手操作，感受这两种拼图的过程，然后再追问一个三角形有几条边？另外两条边呢？在追问引导的过程中，学生的思维从无序变得有序了，经过思考想象、动手操作后，能够将6种图形拼出，并且内心形成了分类标准，教师也能向学生教授分类讨论的数学思想。教师追问学生：“从图形运动的角度思考，这6种图形怎么产生？”看似平常的追问，却是点睛之笔，对学生思维而言是一种拓展，学生在用平移、旋转、翻折这三种变换阐述图形的产生过程中，思维能力得到了提升，进一步理解复杂图形由简单图形组合而成，同时也了解了运动的数学思想。教师采用追问的手段，推动了学生的深入思考，在不断尝试、思考、操作、反思、总结的过程中，学生的逻辑思维不断得到提升，逐步学会用數学的思维思考世界。

教学环节（三）实践与应用：

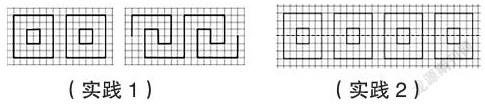
实践1：图2可以看成是图1经过怎样的变化产生的？

师：哪位同学说说看，你是怎么画，怎么想的？

生：要平移这个图形，就要平移组成图形的线段，再想平移线段就是平移点，所以只要将几个相应的点，向右平移四个位置，就可以画出来了。

师：嗯，通过平移，我们发现产生了另一个图形。

实践3：图1可以看成是哪个基本图形经过怎样的运动产生的？

生：图2也是由一个简单的图形旋转而成。

师：换句话说，复杂图形也可以看成由简单图形运动而成。

实践4：用运动的方式研究图形，在点划线一旁空白的方格中画图，使点划线两旁的图形完全相同。谁来分享一下？

生：只要找到对应的点，第一幅图找到1个点，第二幅图找2个点，第三幅图找3个点。只要找出几个对应的点就可以画出了。

师：用运动的观点看这三幅图，这三幅图可以看成是怎样产生的？

生：平移、翻折、旋转都可以产生新的图形。

思考：实践与应用环节的设计有层次，学生在实践操作过程中，逐步感知图形的三种运动（旋转、翻折、平移），都不会改变图形的形状和大小，但会影响它们的位置。在此过程中体现了图形翻折（对称）、图形平移、图形旋转的思想。在实践4中，学生能够想到通过找对应点的方法来画出图形，是前面知识内化的体现。通过剪拼（动态）、割补（静态）等方法，学生对复杂图形由简单图形组合而来有了更深的体会。

三、学会用数学的语言描述世界

教学环节（四）总结与回顾：

1.欣赏一组动态图片。

师：这些图形是怎样产生的？

生：第一幅图是由三角形经过运动产生的，第二幅图的勾股树是由正方形、直角三角形组合产生的，第三幅图是由若干个圆组成的。

2.借助网格设计一个美丽的图案。（手机投屏展示学生的作品）

3.教师用几何画板设计一个由三角形经过翻折、平移、旋转后得到的新的图形，展示改变三角形的元素，图形的形状也会发生改变等。下图是教师作图的几个瞬间。

总结：通过今天的学习，我们发现图形运动可以创造更加美好的图形世界，图形运动是学习研究图形性质的重要方法。

思考：第四个环节的设计是想让学生“学会用数学的语言描述世界”，体现建模的过程，是自内而外的。给学生足够的时间，让学生的思维飞跃，学生欣赏设计的过程，就是思考内化、拓展、升华的过程。最后教师借助几何画板演示将一个三角形经过翻折、平移、旋转后得到许多美丽的图形，再改变三角形的元素，图形也随之改变。学生发出阵阵惊叹声，进一步感知图形运动可以创造更加美好的图形世界，体会图形运动是学习研究图形性质的重要方法。在此环节，笔者有个粗浅的想法：是否可以增加第四个层次，将演示出来的图形应用到现实生活中去，小到衣食住行，大到科技发展，比如建筑学的应用、航空航天材料技术等方面，是不是能够带给学生更多心灵的震撼，让学生的求知欲更加强烈呢？在此过程中让学生充分感受数学学习的价值，体会数学学习的最终目的还是用来解决问题。

四、结语

感谢周海东老师精彩的课堂呈现，真正将“三个理解”的思想落实到教学的每一个环节中去，为笔者主持的苏州市“十三五”规划课题《基于“三个理解”的初中数学教学建构研究》的研究提供了示范和启示。“三个理解”的思想可以落实到数学教学情境设计中，情境的设计要适合学生的学习情况，贴近教学的内容。情境应该是丰富的，教师可以采用现实生活情境、数学情境、科学情境等，情境的使用最终还是为了服务教学内容，帮助学生理解数学。在整节知识的探索过程中，要注重数学知识产生和发展的过程，让学生感悟知识的来龙去脉，参与知识的产生过程，感受数学的历史和文化，让数学不再神秘，使学生理解数学知识存在的合理性、必然性、必要性。同时注重知识的延伸和应用，让学生了解数学知识的作用，感悟学习数学是为了让教学服务于生活，应用于生活，解决现实世界的问题，从而激发学生学习的兴趣，让学生拥有探索精神，培养学生的创造力，这也是学科育人的体现。“三个理解”指导的数学学习与探究活动的目的是让学生实现从“知其然”到“知其所以然”再到“知何由以知其所以然”，是学生理性思维得到良好发展的表现。只有做到理解数学、理解学生和理解教学，才能使数学课堂教学富有生命力，才能让学生的思维得到质的飞跃。基于“三个理解”的教学实践研究，可以助推初中数学教师的专业成长，将教学的理想状态转化为现实状态，使得初中数学教与学的方式得到根本性的转变。

【参考文献】

章建跃. 中学数学课改的十个论题[J]. 中学数学教学参考（上旬）， 2010 （4）： 2-6.

史宁中. 高中数学核心素养的培养、评价与教学实施[J]. 中小学教材教学， 2017（05）：4-9.