加强学生数学阅读能力的培养

文贵双

[摘 要]阅读是获取知识的重要手段.高中数学教学中，教师应教给学生数学阅读的方法和技能，促进学生养成良好的数学阅读习惯，提高学生的数学阅读能力，为学生终身学习打下良好的基础.

[关键词]数学阅读;素养;课内外阅读

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2021）26-0021-03

一、问题的提出

2020年高考结束后，笔者随机访谈了几位考生有关高考数学（全国Ⅱ卷）的考试情况，他们几乎都一致地说：“难！阅读量太大.”其中一个优秀生说道：“第一大题的第（3）、（4）、（12）小题，光读懂题意就要花费许多时间，我一下慌了，后面的题也没有做好.”

这三道题字符数（不计空格）共511个，文字多、数字多、符号多，确实比较难.其实从2018年以来，高考数学的命题由能力立意转为素养立意，试卷凸显综合性和应用性，以反映当下社会的热点和优秀传统文化的真实情境为载体，题目的表述文字增多，增加了对试题理解的干扰项。通过统计全国Ⅱ卷数学理科试题的字符数（不计空格）发现，2018年为1386个，2019年为2271个，2020年为2620个，可以看出逐年增加.

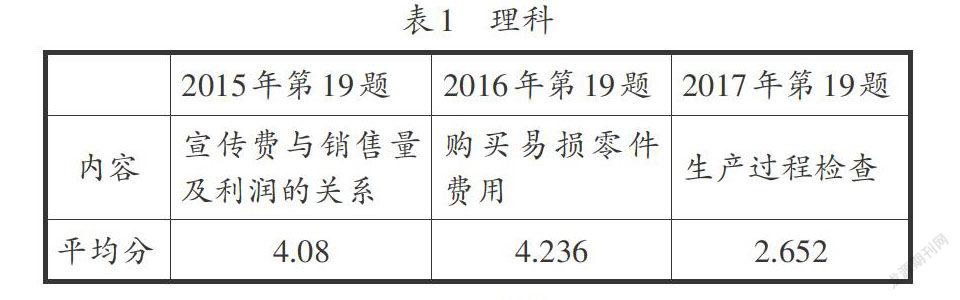
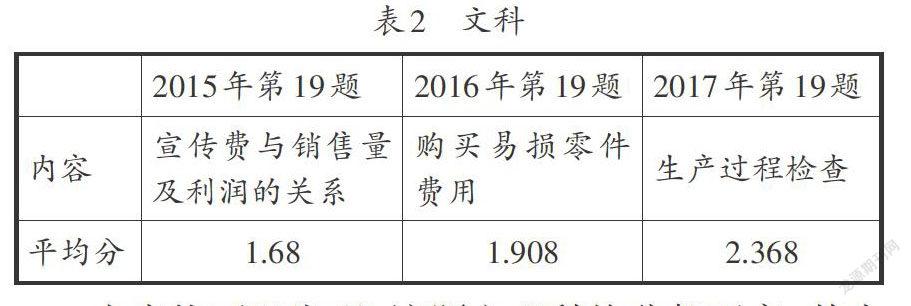
笔者对2015年至2017年全国Ⅰ卷文理科“统计与概率”的高考均分做了统计（见表1和表2）.

由表格可以发现，该题文理科均分都不高.其中2017年文科第19题的均分竟然比解析几何题大题的还要低，实在令人震惊.得分低的一个主要原因是题目文字长，文字语言、图表语言、符号语言交织，学生阅读能力不足，读题费时，理解题意困难.

二、学生数学阅读的现状

在对中学生数学阅读现状进行调查的过程中发现，不阅读课本或者不会阅读课本的现象普遍存在，造成这种现状的主要原因有以下两个方面.

1.教师不重视数学阅读

尽管新课标指出，教师必须指导学生认真阅读课本，但在实际教学中，教师大都不愿留出足够的时间，让学生慢读课本，自主获得知识，而是习惯于告知学生概念，领读一遍题目，然后将大量时间用于解题训练.虽然部分教师也偶尔让学生阅读课本，但学生只是浮光掠影地看，只读文本，只关注表象，没有深度思考，抓不住本质，读不出内涵.正是因为教师没有认识到数学阅读的重要性，不注重培养学生的数学阅读能力，使得学生的数学阅读能力下降.

2.学生阅读时不能准确地掌握和使用数学语言

“数学语言”既具有数学的性质，又具有语言的性质，可归结为文字语言、符号语言、图形语言三类，其特点是准确、严密、简明。由于数学语言是一种高度抽象的人工符号系统，因此，它常成为数学学习的难点.一些学生之所以学不好数学，一个重要的原因是题意理解不当、语言表述紊乱及语言间的转换困难。准确地把握、理解数学语言的精确含义是进行数学阅读的前提，而这正是学生数学阅读的“软肋”之所在.

三、数学阅读能力的培养策略

1.做好阅读引导

教学中，教师应给学生指定阅读内容，并留足时间让学生阅读，其间，通过问题引导学生进行深度阅读.

[案例1]阅读人教A版数学5第二章《数列》章头文字及图示。

《数列》这一章的章头文字如下：

人们对数列的研究有的源于现实生产、生活的需要，也有的出自对数的喜爱.

数是刻画静态下物体的量，例如一棵树在某时刻的高度是2 m.如果在每年的同一时刻都记录下这棵樹的高度，并按自然顺序排列起来，就得到一列数，像这样，接一定顺序排列着的数称为数列.数列可以看成定义在正整数集或其有限子集上的函数，它是刻画离散数过程的重要数学模型.

在日常生活中，人们经常遇到的像存款利息、购房贷款等实际计算问题，都需要用有关数列的知识来解决，数列的知识也是我们将来学习高等数学的基础.

在本章中，我们将学习一般数列的概念和简单表示方法，并将研究两类特殊的数列——等差数列和等比数列，解决与这些数列相关的一些问题，了解它们在实际生活中的应用.

学生阅读完章头文字后，教师可通过提问检查阅读效果.

问题1：从字面如何理解“数列”的概念？说说日常生产和生活中有关数列的例子.

问题2： 这段文字提到等差数列和等比数列两类特殊的数列，你如何理解“等差”“等比”？是否有“等和”数列？

《数列》一章的引言部分配备了几个图案：树木的分杈、向日葵的花瓣、蒲公英、松果塔、菊花等，并配有一段话：有人说，大自然是懂数学的，不知你注意过没有，树木的分杈、花瓣的数量、植物种子或树木的排列……都遵循了某种数学规律.你能发现下面这个数列与这种规律的关系吗？

1，1，2，3，5，8，13，21，34，55，89，…

问题3：从章头图中你读到什么？树木分杈有什么规律？

问题4 ：你能解释文中提到的规律是什么意思吗？

学生讨论后，教师再提供如下材料供学生阅读：

此章头图蕴含着一个非常重要的规律——大自然里的斐波那契数列.这些植物懂得斐波那契数列吗？应该并非如此，它们只是按照自然的规律才进化成这样.

仔细观察向日葵花盘，你会发现两组螺旋线，一组沿顺时针方向盘绕，另一组则沿逆时针方向盘绕，并且彼此镶嵌.虽然不同的向日葵品种中，种子顺时针方向、逆时针方向螺旋线的数量有所不同，但往往不会超出34和55、55和89或者89和144这三组数字，这每组数字都是斐波那契数列中相邻的两个数.前一个数字是顺时针盘绕的线数，后一个数字是逆时针盘绕的线数.1992年，两位法国科学家通过对花瓣形成过程的计算机仿真实验，证实了在系统保持最低能量的状态下，花朵会以斐波那契数列长出花瓣.

树木的叶子的生长方式也是如此，对于许多植物来说，每片叶子从中轴附近生长出来，为了在生长的过程中一直都能最佳地利用空间（要考虑到叶子是一片一片逐渐地生长出来，而不是一下子同时出现的），每片叶子和前一片叶子之间的角度应该是222.5度，这个角度称为“黄金角度”，因为它和整个圆周360度之比是黄金分割数0.618033989……的倒数，而这种生长方式就决定了斐波那契螺旋的产生.

因为植物所显示的数学特征是植物生长在动态过程中必然会产生的结果，它受到数学规律的严格约束，换句话说，植物离不开斐波那契数列.

通过这些背景资料，使学生充分理解大自然的丰富多彩，感受“大自然是懂数学的”，使学生感受到即将学习的数列内容充满了大自然的奥妙和神奇，激发了学生的求知欲，增强了学生的审美能力，让学生充分感受和欣赏数学美，从中体会到数学是有用的，数学就在我们身边，应认真学好数学.

2.选适当的内容编写学历案引导学生阅读

教学中，教师应选择适当的内容编写成学历案，然后放手让学生自主阅读理解教学材料.为避免学生阅读“肤浅化”，教师可以在学历案中设置一些问题，让学生进行深度思考，同时组织学生讨论交流，互相补充阅读中的不足.

[案例2]《2.4  等比数列》学历案（提纲）

问题1：你能类比等差数列的定义，得出等比数列的定义吗？如何认识常數列？

问题2：等差数列的通项公式是归纳得出的，你如何通过归纳的方法得出等比数列的通项公式？

问题3 ：等差数列的通项公式可以这样得出：[a2-a1=d]，[a3-a2=d]，[a4-a3=d]，…，[an-an-1=d].以上各式相加，得[an-a1=（n-1）d]，故有[an=a1+（n-1）d].此种方法我们称作“累加求通项”.仿此方法，等比数列的通项公式如何得出？此种方法可起什么名？

问题4：你能类比等差中项，得出等比中项吗？

问题5：等差数列[an]中，[m、n、p、q∈N*]，

（1）若[m+n=p+q]，则[am+an=_________].

（2）若[m+n=2p]，则[am+an=_________.]

（3）设数列[an]的前n项和为[Sn]，则[Sm，S2m-Sm，S3m-S2m，…]成等差数列，类比到等比数列，有哪些性质？

……

数学阅读不光是把材料看一遍，更要看出材料中的“深意”来，这就要求“深度阅读”.“深度阅读”以知识深度加工、意义建构、迁移应用为主要特征，以理解、分析，应用、推广、评价、创造等高层次的认知活动为主要的学习活动.本学历案通过问题引领学生步步深入阅读而完成学习，通过问题2、问题3，学生懂得了归纳可得出等差数列、等比数列的通项公式，而且掌握了“累加求通项”“累积求通项”的方法以及题型的特点.问题5引导学生得出等比数列的性质，但是性质（3）“设等比数列[an]的前n项和为[Sn]，则[Sm，S2m-Sm，S3m-S2m，…]成等比数列”在特殊情况下不成立，学生难以注意到，这时教师要舍得花时间让学生讨论辨析，教师的指导不可缺失.

教师编写学历案，巧设问题引导学生阅读，培养了学生的数学阅读能力.

3.安排多种形式的课外阅读活动

高中生几乎没有时间阅读数学课外书籍，为此，教师应安排多种形式的课外阅读活动，教师可事先拟定阅读提纲或者思考的问题，让学生课后带着问题去阅读，然后指导学生写阅读体会，再组织学生交流，同时督促检查并评价.

[案例3]我校高一、高二每周自习安排一次社团活动，我们备课组组建《数学史赏析》社团，给学生提供《数学的魅力》《从一到无穷大》《数学家的眼光》等课外数学书籍，并指导学生阅读，然后让学生汇报阅读体会.

社团活动期间，教师又安排一些任务，学生准备材料做成PPT，供大家交流分享.其中有如下的选题：《田忌赛马中的数学知识》《分形几何学之美》《晶体与正多面体》《2018全国2卷作文材料中的数学问题》《数字背后的陷阱》《购房中的数学知识》等.

这样的课外阅读活动，可以提高学生的阅读兴趣、引发学生的求知欲、调动学生的学习积极性;可以拓展学生数学知识视野，让学生体会数学的内在美，感受数学学科的魅力.

综上，数学阅读是学生自主获得知识的过程，也是从材料中获取信息的心理活动过程，不仅包括对数学语言、符号、图表的感知、认读、记忆、理解等过程，还包括对材料进行分析、综合、归纳、推理、猜想等一系列思维过程，是区别于一般阅读的较为高级的智力活动.数学阅读不同于一般阅读，数学阅读要经历数学抽象、直观想象、逻辑推理、数学运算、数学建模、数据分析等，因此，加强数学阅读能力的培养，可以提高学生的数学核心素养和积淀学生的数学文化底蕴，为学生的终身学习打下良好的基础.

[   参   考   文   献   ]

[1]  苏霍姆林斯基.给老师的建议[M].北京：教育科学出版社，1984.

[2]  任子朝，陈昂，赵轩.加强数学阅读能力考查展现逻辑思维功底[J].数学通报，2018（7）：8-13.

（责任编辑 陈   昕）