拓展性作业，打开“阅读材料”教学的另一扇窗

王强强

摘  要：改革作业形式，尝试以拓展性作业的形式分组研讨阅读材料，转变阅读材料为简单的材料阅读这一教学现实困境，允许学生就阅读材料上的问题或与之相关的问题自由拓展，以拓展促进深度学习，突破学科知识的年段限制和课堂时间与空间的束缚，促使阅读材料能真正成为体现学生自主探究、合作交流、拓展学习内容、转变学习方式的另一主阵地.

关键词：拓展作业;阅读材料;课堂教学

一、引言

浙教版《义务教育教科书·数学》（以下统称“教材”）中，专设“阅读材料”栏目，所附材料一般是教材相关内容的引申、拓展及综合，意图通过观察、实验、比较、归纳、猜想、推理、反思等理性思维活动，促使学生积累活动经验、展现思考过程、交流收获体会、激发创造潜能.

然而，阅读材料一直困扰着广大一线教师：栏目需不需要展开教学？材料值不值得花精力去探究？内容是否适宜于当下实施？有无更好的教学活动展开方式？于是，很多时候阅读材料就被师生“一翻而过”“一看而越”，并未真正做到“深入学习与研究”.

究其原因，一是教师对阅读材料所涉及内容设计的理解普遍不到位，阅读材料应该成为体现合作、探究等学习方式的有效载体，不仅只是为学生提供从自主探索到合作交流的平台与机会，更是赋予学生通过自己的经验来构建知识的方法，突破学科知识的年段限制和课堂时间与空间的束缚，在创造性使用的过程中呈现教材价值. 二是阅读材料的教学要力争还原学生的学习全过程，并不只是人们通常所说的阅读教材，而是通过思考与体验，来帮助理解，实现感悟与提升. 它有别于学习具体知识的探索活动，反映背景、重视过程、加强应用，承载着拓展学习内容、体现学习方式转变、实施过程性评价的任务. 三是尊重学生的层次差异，阅读材料的学习评价更多的是關注学生在学习过程中自身素养的发展与变化，满足学生对相关知识理解的个性化需求，实现不同的人在数学上得到不同的发展.

笔者尝试将阅读材料的内容以拓展性作业的形式作为小组学习任务布置给学生，让学习小组自行确定一个研究方向、选定任务（自己感兴趣的或认为有价值的、有挑战性的），从探究、验证、综合到展示都由学生自主组织活动（允许学生在较长时间内完成），使单一课时教学的影响延续到后续较长时间内的学习与生活之中，以作业拓展促进简单学习向深度学习转变.

二、教材呈现

我们知道，勾股定理反映了直角三角形三条边之间的关系：a2 + b2 = c2. 而a2，b2，c2又可以看成是以a，b，c为边长的正方形的面积. 因此，勾股定理也可以表述为：分别以直角三角形两条直角边为边长的两个正方形的面积之和，等于以斜边为边长的正方形的面积. 如图1，S1 + S2 = S3. 如果以直角三角形的三条边a，b，c为边，向形外分别作正三角形（如图2），那么是否存在S1 + S2 = S3呢？类似地，上述结果是否适合其他图形？例如，图3是分别以直角三角形的三边为直径作半圆，则S1 + S2 = S3成立吗？再画几个类似的图试一试，结论成立吗？

三、作业要求

仔细阅读教材八年级上册第二章“特殊三角形”第7节“探索勾股定理”（第2课时）课后的阅读材料：从勾股定理到图形面积关系的拓展（第78 ～ 79页），然后以小组为单位，就你最感兴趣的内容进行探究与拓展，时间为一周，一周后进行小组展示.

四、拓展作业展示

成果展示1：证明材料中两个猜想的正确性.

（1）以直角三角形的三条边a，b，c为边，分别向外作正三角形，必定存在S1 + S2 = S3.

成立理由：[S1=12a · 32a=34a2.] 同理，可得[S2=][34b2，S3=34c2.] 因为a2 + b2 = c2，所以S1 + S2 = S3.

（2）以直角三角形的三条边a，b，c为直径，分别向外作半圆，S1 + S2 = S3依然成立.

成立理由：[S1=12π · a22=12π · 14a2=π8a2.] 同理，可得[S2=π8b2，S3=π8c2.] 因为a2 + b2 = c2，所以S1 + S2 = S3.

A组结论：我们小组只是证明了阅读材料图2、图3中所表述的命题成立. 但对教材中关于欧几里得《几何原本》第六卷命题31“在一个直角三角形中，在斜边上所画的任何图形的面积，等于在两条直角边上所画的与其相似的图形的面积之和”存在质疑，没能给出合理的解释.

成果展示2：向外拓展发现勾股树.

（1）分别以Rt△ABC三边a，b，c为边向外作正方形，面积为S1，S2，S3，以此向外再作一层正方形，面积为S4，S5，S6，S7. 如图4，发现S3，S4，S5，S6，S7之间的数量关系为S3 = S4 + S5 + S6 + S7.

（2）如图5，以此向外再作一层正方形，发现S3，S8，S9，S10，S11，S12，S13，S14，S15之间的数量关系为S3 = S8 + S9 + S10 + S11 + S12 + S13 + S14 + S15.

B组结论：最外层的正方形面积之和等于最下边的正方形面积. 最外层的正方形的数量是无限的，但是这无限个正方形的面积之和必为定值，即为最初那个正方形的面积. 画出一个可以无限重复的图形，形状好似一棵树——勾股树.

除此之外，B组还有如下发现.

（3）如图6，将直角三角形拓展为对角互补的四边形ABCD，且∠DAB = ∠BCD = 90°，分别以四边形的四条边向外作四个正方形，面积分别为S1，S2，S3，S4，那么必然存在S1 + S4 = S2 + S3.

（4）如图7，将勾股定理在三维空间中进行延伸，分别以Rt△ABC三边a，b，c为边向外作正方形，并以此正方形为底面向上再作高均为d的长方体，体积分别为V1，V2，V3，发现V1，V2，V3之间的数量关系为V1 + V2 = V3.

B组结论：图6、图7为“特殊的四边形”“特殊的立体图形”中相似命题的成立提供了一个案例.

成果展示3：将图形进行对折与拼接.

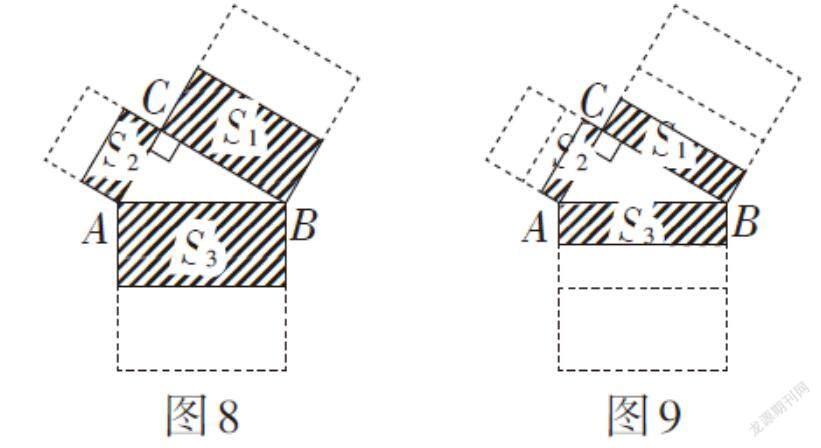
（1）如图8，分别以Rt△ABC三边a，b，c为边向外作正方形，然后将每个正方形进行一次对折，发现S1 + S2 = S3仍然成立. 若在此基础上，再进行一次对折，如图9，S1 + S2 = S3仍然成立.

进一步探究：若将每个正方形沿它的对角线对折一次（如图10）、对折两次（如图11）、取特殊点（如图12）等，发现S1 + S2 = S3仍然成立.

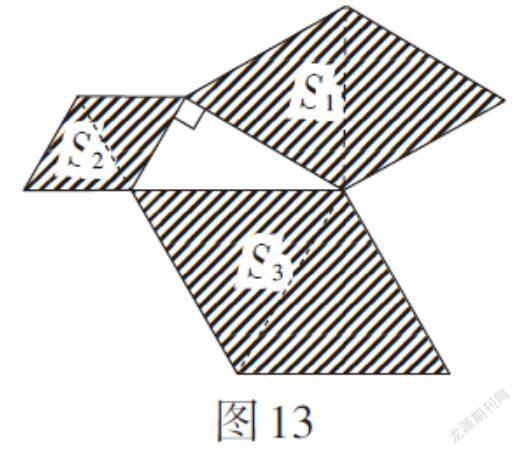
（2）分别以Rt△ABC三边a，b，c为边向外作正三角形，然后将每个正三角形向外翻折，如图13，则S1 + S2 = S3成立. 若在此基础上，再将图形进行拼接，S1 + S2 = S3仍然成立.

C组结论：在一个直角三角形中，在斜边上所画的任何图形的面积，等于在两条直角边上所画的与其形状相似的图形的面积之和.

成果展示4：改变图形位置.

（1）如图14，将Rt△ABC的直角边BC放置在直线l上，以斜边AB为边作正方形ABEF，过点E作ED⊥l于点D，再以AC，DE为边分别作正方形. 运用全等三角形的性质，可得S1 + S2 = S3.

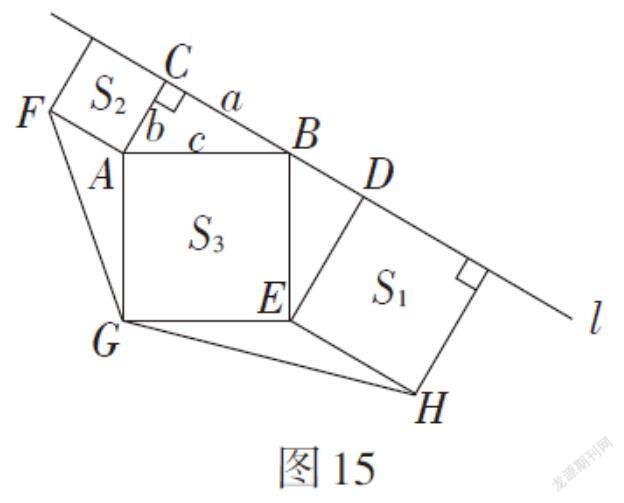
（2）如图15，推理得△ABC，△BDE，△EGH，△AGF面积相等.

如图16，进一步可得，夹在两正方形之间的上、下两个三角形面积相等. 例如，△ABC与△ADE的面积相等.

（3）以直角三角形的各边为边分别向外作正方形，再把较小的两个正方形按如图17所示的方式放置在最大的正方形内. 发现，图中阴影部分的面积一定等于较小两个正方形重叠部分的面积.

（4）以直角三角形的各边为边分别向外作正三角形（等腰直角三角形或半圆），再把较小的两个正三角形（等腰直角三角形或半圆）按如图18所示的方式放置在最大的正三角形（等腰直角三角形或半圆）内，发现较大图形中未被覆盖（图中阴影部分）的面积等于两个较小图形的重合面积.

（5）若将图3中最大半圆沿直角三角形斜边向上翻折得到图19，则有S1 + S2 = S3.

（6）若将图2中的最大正三角形沿直角三角形斜边向上翻折得到图20，则有S1 + S3 = S2 + S4.

（7）若将图1中的最大正方形沿直角三角形斜边向上翻折得到图21，则有S1 + S2 + S4 = S3 + S5.

D组结论：在一个直角三角形中，分别以三边做相似图形，将斜边上所画的图形向上翻折，舍去重叠部分，剩余部分仍符合这样的面积关系.

成果展示5：尝试作相似图形进行探究.

（1）分别以直角三角形两条直角边为边长的两个正三角形的面积之和等于以斜边为边长的正三角形的面积.

进一步探究：如图22，发现分别以直角三角形两条直角边为边长的两个正六边形的面积之和等于以斜边为边长的正六边形的面积.

（2）分别以直角三角形两条直角边为底边的两个等腰三角形的面积之和不一定等于以斜边为底边的等腰三角形的面积.

进一步探究：发现若所作的三个等腰三角形的高与底之比相等或腰与底之比相等，则结论仍然成立.

（3）分别以直角三角形两条直角边为边长的两个正五边形的面积之和等于以斜邊为边长的正五边形的面积.

成立理由：可以将每个正五边形分解成五个等腰三角形，其均为等腰三角形，且腰与底之比相等，故结论仍然成立.

（4）分别以直角三角形两条直角边为边长的两个正n边形的面积之和等于以斜边为边长的正n边形的面积.

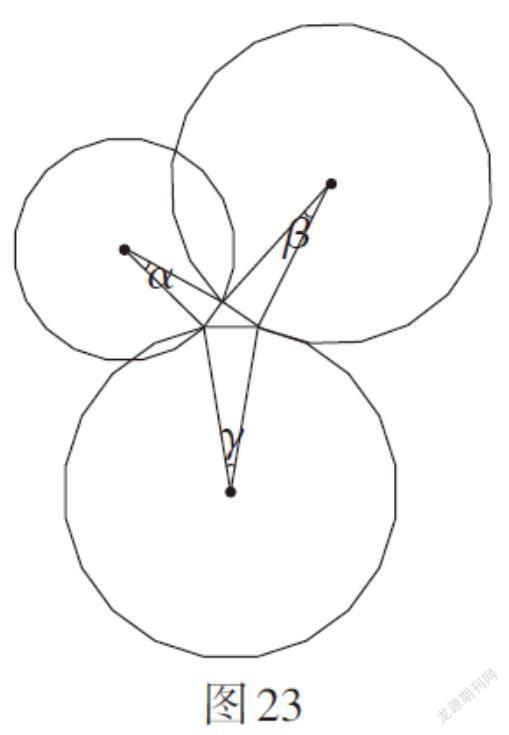
进一步探究：如图23，发现随着所作正n边形的边数不断增加，正n边形逐渐接近于圆，且无论何时，中心角[α=β=γ]始终成立，因此S1 + S2 = S3始终成立. 特别地，如果以直角三角形的三条边a，b，c为直径，向外分别作半圆（如图3），那么S1 + S2 = S3依然成立.

在查阅有关相似图形的学习资料后，我们了解到，与相似三角形类似，相似多边形的周长之比等于相似比;相似多边形的面积之比等于相似比的平方.

E组结论：在一个直角三角形中，在斜边上所画的任何图形的面积，等于在两条直角边上所画的与其相似的图形的面积之和.

五、教学反思

1. 突破课时教学局限，在创造性使用过程中凸显教材的价值

教材是体现教育思想的工具，不能把教材看成是对教学内容的规定，更不能把教材看成是对教学内容的限定. 本课例中，学生紧扣阅读材料的主体内容“图形面积关系的拓展”，以小组合作的形式展开学习任务. 突破单一课时教学内容的局限，允许学生就阅读材料上的问题或与之相关的问题自由拓展，对教材内容进行重新整合、补充，甚至延展.

有的小组立足“向外作正方形”这一基本图形探究了勾股树，引发改变图形数量后的面积猜想——最外层的正方形的数量是无限的，但是这无限个正方形的面积之和必为定值，即最初那个正方形的面积;有的小组基于材料中关于欧几里得《几何原本》第六卷命题31文本描述的疑问，展开图形探究，引发相似图形面积猜想——一个直角三角形中，在斜边上所画的任何图形的面积，等于在两条直角边上所画的与其相似的图形的面积之和;甚至有的小组在相同形状的基础上展开进一步的探究——图形翻折与变换，引发改变图形位置后的面积猜想.

2. 改革作业形式，把构建知识的过程还给学生

积累数学活动经验、培养学生的应用意识和创新意识是数学课程的重要目标，应贯穿于数学教学的始终. 因此，我们主张还原学习全过程，不能与平时的作业同质化. 变习题操练为基于任务的问题解决过程，以问题拓展为载体促进学习方式的转变（如图24），它是学生通过问题引领，全程参与、思考、交流与实践过程相对完整的学习活动，整个学习进程呈阶梯式螺旋推进，促进学以致用.

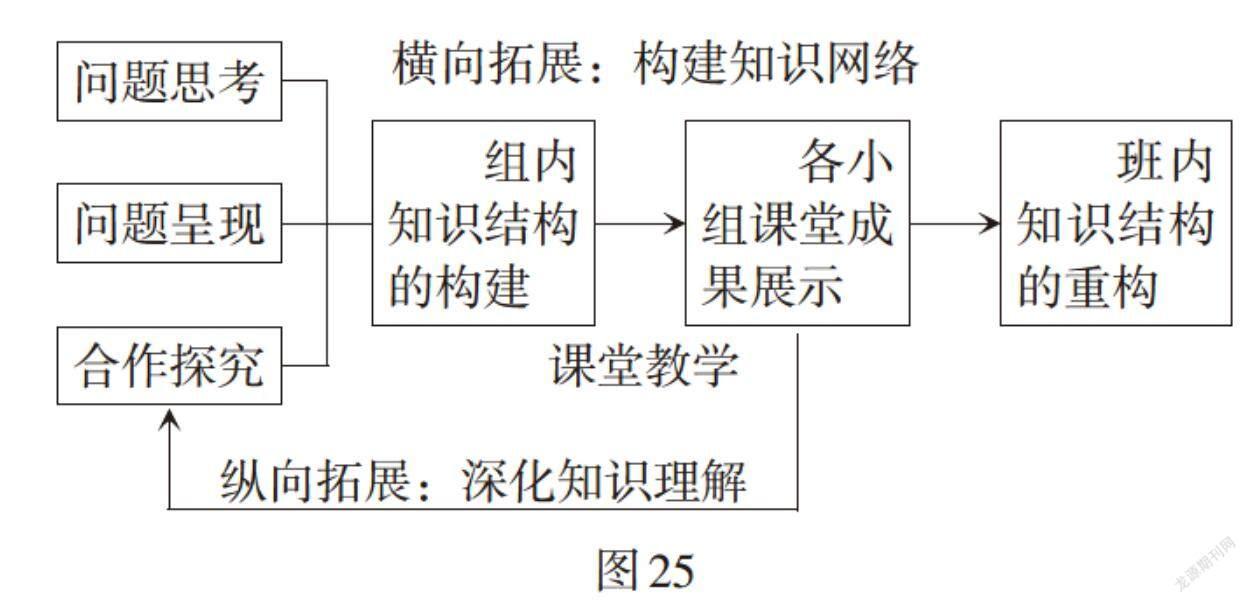
先就组内学生独立思考，而后组内讨论，形成研究方向，最后达成共识，确定本组接下来近一周的拓展学习任务，将零散的学习转化为有组织的知识建构，观察、积累、分析、反思，使作业拓展的实施成为提升学生自身及小组内外乃至全班学生素养的互动过程，如图25所示. 既注重学生自主参与、全过程参与，又关注数学与生活实际、数学与其他学科、数学内部知识的联系和综合应用.

打破原来阅读材料仅仅是教材阅读的尴尬局面，努力通过集体思考与多样化的、拓展性体验，来达成促进理解与提高能力的平衡，实现真正意义上的以学生个性发展为本的学习过程，实现不同思维层次的学生（或学习小组）在数学上得到不同的发展.

参考文献：

[1]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2]格兰特·威金斯，杰伊·麦克泰. 理解为先模式：单元教学设计指南（一）[M]. 盛群力，沈祖芸，柳丰，等译. 福州：福建教育出版社，2019.

[3]马复. 关于促进学生数学活动经验的教学认识[J]. 中国数学教育（初中版），2011（10）：2-5.

[4]黄邦杰，王学先. 新课标、新理念、新策略：谈2013年中考数学基础复习[J]. 中国数学教育（初中版），2013（1 / 2）：7-26.