基于深度教学U型模式的教学设计改进

庞新军，刘若男

摘  要：对一节教学效果不太理想的课进行反思，分析教学设计中存在的问题，以深度教学中的U型模式作为理论基础，对教学设计进行再加工、再创造. 通过前后两次教学设计的对比，达到深度教学，改进教学过程中存在的问题，实现对教学活动的理性思考.

关键词：深度教学;U型模式;教学设计;改进

一、问题缘起

一节优质的课总让人很难忘怀，而一节平庸的课也同样让人无法释怀. 笔者曾观摩了一节九年级“旋转计算”专题课，虽然教学重点比较突出，但教学难点没有真正突破，整体教学效果不太理想. 从学生核心素养来看，数形结合能力和空间想象能力有所欠缺，数学知识运用意识薄弱，直观想象核心素养渗透不足. 本文借助深度教学理论中的U型模式对教学设计进行调整和改进，旨在通过对前后两次教学设计的分析对比，修正教学过程中存在的问题，实现对教学活动的理性思考，提升教师的理论水平和教学能力.

1. 第一次课的教学设计

下面展示第一次课的教学设计中的四个教学环节和教学内容.

（1）小试牛刀.

练习1：如图1，D是等腰直角三角形[ABC]内一点，BC是斜边，如果将[△ABD]绕点A逆时针旋转到[△ACD]的位置，则[∠ADD]的度数为         .

练习2：如图2，在[△ABC]中，[AB=6，BC=11，] [∠B=][60°，] 将[△ABC]绕点A按顺时针旋转一定角度得到[△ADE]，当点B的对应点D恰好落在边BC上时，则CD的长为      .

练习3：如图3，在等腰直角三角形[ABC]中，[∠C=90°，] [BC=23 cm，] 将[△ABC]绕点A顺时针旋转15°后得到[△ABC，] 则图中阴影部分的面积为      .

【设计意图】限时训练，在学生完成3道练习题的解答后，教师引导学生复习旋转的三条基本性质. 通过练习题，复习回顾旋转的基本性质，为图形旋转和计算做好铺垫.

（2）典例讲解.

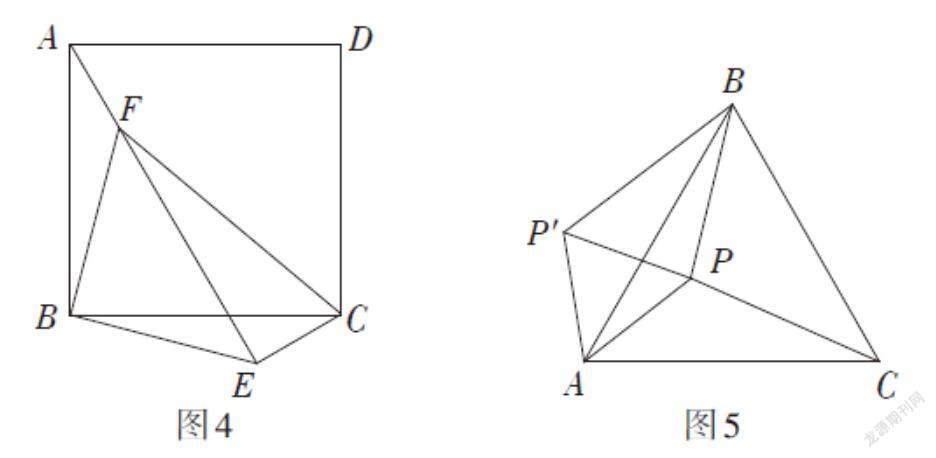
例1  如图4，点E在正方形ABCD外，[BE=4，][CE=2，] [∠BEC=135°，∘] 将[△BEC]绕点B逆时针旋转得到[△BFA]，求[FE，FC]的长.

例2  如图5，[P]是等边三角形[ABC]内的一点，且[PA=][3，] [PB=4，PC=5，] 若将[△PAC]绕点A逆时针旋转后，得到[△PAB，] 则[PP]的长为______，[∠APB]的度数为______.

【设计意图】学生独立思考，小组讨论交流. 学生在交流中学会解决问题和规范答题. 教师引导学生发现旋转过程中的规律和“共顶点的等线段”的处理方法. 通过自主探究，发挥学生的主观能动性，加固对旋转基本性质的应用，提高学生的分析能力.

（3）能力提升.

题目1  如图6，点[D]是以[AB]为斜边的等腰直角三角形[ABC]内一点，且[BD=1，CD=2，AD=3，] 求[∠BDC]的度数.

【设计意图】学生动手操作，添加辅助线，独立完成解答. 教师指导部分学生添加辅助线，将三角形进行旋转. 通过添加辅助线，让学生感受图形的旋转过程，体会运动变换中的规律.

（4）直击中考.

题目2  如图7，在四边形[ABCD]中，[∠B=60°，][∠D=][30°，AB=BC.]

（1）求[∠A+∠C]的度数;

（2）连接[BD，] 探究[AD，BD，CD]三者之间的数量关系，并说明理由.

【设计意图】此题为2018年中考广州卷第25题的前两道小题，让学生体会旋转在解决线段之间数量关系中的作用，巩固对知识的理解和应用. 教师展示优秀解答过程，规范答题细节. 通过对中考试题的解答，消除学生对中考的恐惧心理，树立学习数学的自信.

2. 课后分析与思考

课后执教教师谈到，本节课的练习题和例题推进得比较顺利，教师讲解清晰，学生通过做题能掌握由旋转得到的简单模型，能发现题目中直接给出的等腰直角三角形、等边三角形、含30°角的直角三角形等特殊图形. 但从题目1开始，课堂教学就陷入了困境，偏离了执教教师的预设，大多数学生在把目标放在三角形旋转上以后，不能正确地连接线段构造出特殊三角形，甚至有一部分学生连需要旋转的三角形也未找到. 无奈之下，教师包办了后面的所有教学，从而导致教学难点无法突破. 回顾分析课堂教学中各环节的衔接，会发现教学设计的内容方面存在一些问题，“小试牛刀”中的3道练习题重复单一，没有让学生感受到图形的动态变化，对之后教学的辅助作用较弱.“典例讲解”与“能力提升”之间跨度太大，缺少梯度，没有考虑到学生的思维最近发展区. 以上教学设计的情境，并不能通过位置关系、形态变化与运动规律来揭示数学直观的本质，不足以提升学生的直观想象和逻辑推理素养. 要想提升学生的直观想象素养，就要借助几何直观和空间想象帮助学生感知事物的形态与变化，利用空間形式，特别是图形，建立形与数之间的联系，构建数学问题的直观模型，探索解决问题的思路.

另外，在“典例讲解”环节，教师虽然给了学生时间探索，课堂气氛看起来很热闹，但“出现‘共顶点等线段’可以尝试旋转”这一结论是由教师直接提出的，学生并没有经验投入、情感投入、思想投入和实践投入等多样化的学习投入，只完成了对基础知识的简单占有. 绝大多数学生没有把旋转变成自己的认知对象，也就无法进行后期的知识迁移，进而导致学生对题目1和题目2的求解无从下手. 单一的知识授受和解题训练，或者课堂表层的活跃，仍然属于“浅层学习”的范畴. 活动与体验是深度学习的核心特征，深度学习是学生主动参与、亲身经历，获得知识的深度理解，获得知识的意义增值，获得数学学科核心素养发展的过程. 因此，提升学生学习的强参与性、探究与体验，必须依靠教师对教学内容和教学过程的精心设计.

二、U型教学模式

深度教学是激发学生发生深度学习的师生共同活动，可以改变目前课堂教学中普遍存在的知识表面化、思考表层化、交流表演化的状况. 深度教学不仅关注学生学科知识的获得，更关注学生学科思想的形成及学生个人的发展. 因此，深度教学是教师发挥主导作用，基于知识的本质特征设置具有挑战性的学习主题，教师带领学生积极参与教学的各个环节，通过学生主动探究、合作交流，在问题解决中从促进知识向学生的核心素养转化，通过教学的过程性实现知识的教育价值.

美国著名教育学家杜威认为，学生不亲身经历活动体验知识的生成，只通过听课和读书无法真正获得知识. 对学生而言，学习是一个复杂的、需要深度体验的过程，这个复杂的过程可以分为下沉与还原、潜行与探究、上浮与应用三个阶段. 这三个阶段就像一个“U型”（如图8）. 因此，杜威的经验教学理论从教学过程看可以概括为U型教学模式.

第一个阶段：下沉与还原. U型模式是沉浸式学习，下沉是U型模式的入口. 任何新知识的学习都建立在学生已有认知的基础上，这一阶段教师设置问题激活旧知，唤醒学生对人类历史认识成果的个体经验，还原知识的原貌，追踪知识的进化历程，激发学生进入深度学习状态.

第二个阶段：潜行与探究. 潜行是U型模式的底部，是判断深度学习是否发生的关键期，教师设置一系列有梯度的学习任务，根据学生的反应进行有针对性地指导，借助问题串促进学生不断达成探究目标，体验问题解决的学科方法. 学生在独立思考与协作探究中完成对知识的深度加工，建构新的知识网络与认知体系.

第三个阶段：上浮与应用. 上浮是U型模式的出口，学生在经历上一阶段的理解、体验、探究和交流等活动后，在这一阶段通过元认知活动对学习过程进行反思与领悟，重新审视知识并在知识中融入个人的理解，建立知识的意义系统，获得知识的意义增值，实现知识的迁移运用. 这个过程是检验与反思的过程，也是知识的表达与运用，以及外显的过程.

三、教学设计改进

《义务教育数学课程标准（2011年版）》将“图形与变换”调整为“图形的变化”，更重视图形的运动，对初中几何三大运动之一的旋转提出了更高的要求，即通过具体实例认识平面图形的旋转，探索旋转的基本性质，能运用旋转的知识解决简单的问题. 这些要求既包含了掌握旋转的基本性质、运用旋转解决简单的问题等显性的基础知识与基本技能，也包含了从特殊到一般、从具体到抽象、合作探究旋转的基本性质等隐性的基本思想与活动经验，以上要求都可以通过深度学习来实现.

1. 下沉与还原——还原旋转的本质，关注图形的变化

下沉与还原是U型模式的入口，教师应该根据学生原有的知识水平，遵循学习规律、指向学习目标设计问题，使学生在问题解决中自觉还原旋转的本质，关注图形的变化，增强学生对旋转的三条基本性质的理解，引领学生进入深度学习状态. 学生学习图形的旋转要注重从旋转的角度刻画静止图形之间的关系，以及按要求作出发生旋转变化的图形. 原教学设计只注重了前者，没有下沉到图形的变化. 因此，后续教学无法引发学生的深度学习. 因此，对这一阶段的教学设计进行了如下调整.

练习1：同原教学设计中练习2.

练习2：如图9，在[△ABC]中，[∠C=90°.∘]

（1）将[△ABC]绕点[B]逆时针旋转90°，画出旋转后的三角形;

（2）若[BC=3，AC=4，] 点[A]旋转后的对应点为[A]，求[AA]的长.

师生活动：学生画[△ABC]绕点[B]旋转. 方法：从点到线段、再到三角形. 复习旋转的性质. 使学生在师生对话中自主发现当旋转角是60°时，连接对应点会出现等边三角形;当旋转角是90°时，连接对应点会出现等腰直角三角形. 教师倾听学生的解答. 用软件演示练习2中[△ABC]旋转的过程，设计如下问题.

问题1：练习1中，若点[B]的对应点[D]没有落在边[BC]上，判断[△ABD]的形状.

问题2：练习2中，记点[C]旋转后的对应点为[C，][CC]的长可求吗？

预设成果：将原教学设计“牛刀小试”部分3道重复的练习题改为两道，从两个层面唤醒、还原学生的经验，练习1从旋转的角度认识静态图形，练习2要求学生作图，求旋转对应点所连线段. 帮助学生从单纯的解题“下沉”到对图形变化的关注，重视分散线段的集中，为下阶段的“潜行与探究”做好准备.

修改后的下沉与还原阶段，较好地体现了教师对学生思维最近发展区的把握，将新授知识与学生已有认知基础建立起密切联系，激发学生的学习动机.

2. 潜行与探究——探究一般规律，让变化主动发生

潜行与探究发生在U型模式的底部，教师以例题为载体，通过设疑、质疑、解疑，逐步引导学生对新授知识进行深度加工，是发展学生高阶思维能力，提升学生几何直观、推理能力和运算能力的过程. 学生在教师的引导下，达到按题目要求旋转图形，解决旋转形成的特殊图形及衍生图形的问題，以及根据题目需要和图形特征主动旋转图形，形成新的图形关系两个层面. 原教学设计只注重前者，而忽略了后者. 因此，对教学设计进行了如下修改.

（1）深入思考，发现特殊图形的旋转规律.

在学生的解题活动与内在思维活动之间有着十分重要的联系，什么情况需要旋转？该怎么旋转？旋转后怎么办？学生只有围绕这些问题进行深入思考，相应的解题行为才能被看成真正的活动. 为此，将原教学设计中例2的设计从知识立意和能力立意改进为活动立意和思想立意，由直接给出图形改为让学生自己作图，发挥学生的主观能动性，推动学生在旋转形成的特殊图形及衍生图形中潜行.

例1  同原教学设计中例1.

例2  如图10，[P]是等边三角形[ABC]内的一点，且[PA=][3，PB=4，PC=5.]

（1）将[△APC]绕点[A]逆时针旋转60°，画出旋转后的三角形;

（2）记点[P]旋转后的对应点为[P]，连接[PP]，求[PP]的长和[∠APB]的度数.

学习任务：说出例1中点[E]的对应点. 连接对应点[EF]所得[△BEF]的形状，以及[△CEF]的形状. 说出例2中连接对应点[PP]所得[△APP]的形状，以及[△BPP]的形状. 若给出题设条件后直接求[∠APB，] 你是否还有其他方法？

教师行为：教师组织学生探究、讨论、演算、交流、再思考，发现解决此类问题的两个步骤. 第一步，借助“共顶点的等线段”可旋转得到等腰直角三角形或等边三角形;第二步，旋转后可尝试连接对应顶点构造特殊图形.

预设成果：结论在教师的追问和学生的思考、探究、讨论、交流、反思中自然生成，这样的生成方式顺应学生的思维发展，学生容易接受，也容易使学生获得成功感，提升自我效能感.

（2）变式练习，层层深入提升能力.

变式练习是指围绕本节课的核心概念，通过改变题目条件和设问方式等方法引导学生从多个角度、用不同方法分析问题和解决问题，实现在新知识结构范围内对知识形态进行迁移. 有效的变式练习可以帮助学生克服思维定势，实现创新目标. 学生从不同途径寻求问题的解决，层层深入追寻旋转的本质，实现“根据题目需要和图形特征主动旋转图形形成新的图形关系”的突破.

设置题目为原教学设计中题目1.

师生活动：学生将[△ACD]绕点[C]逆时针旋转90°得[△BCD]求解，或将[△BCD]绕点[C]顺时针旋转90°得[△ACD]求解. 教师展示不同解法、师生共同点评，与学生一起归纳不同解法的相通之处. 尝试旋转其他三角形，目标角无法拆分，问题无法解决.

预设成果：在逐级强化的题目解答过程中提升学生的抽象能力，培养学生从变换的高度分析问题的能力，以及用运动的观点看待图形的能力，以一题多解促进学生发散性思维的形成.

修改后的潜行与探究阶段，较好地体现学生通过独立思考、认知会话、协作探究完成对知识的深度加工，构建新的认知与理解，对知识的认识从符号特征深入到逻辑形式，发展学生的高阶思维，提升学生的直观想象和数学运算素养.

3. 上浮与应用——思维形成，内化的知识外显

上浮与应用是U型模式的出口，既是教师对前半段教学效果的诊断与评价，继而做出后续教学调整的依据，也是学生反思性思维和批判性思维的形成过程. 经过反思，学生将教材知识进行个人意义的升华和表达，使教材知识真正进入学生的知识结构. 原教学设计只注重优秀作答的展示与教师讲解等单向输出，多数学生的课堂参与度不足，反思不强. 因此，对教学设计做出了如下改进：教师以“不教”代替“教”，通过点撥、指引、提升和点评，使学生在生生交流、师生交流中锻造思维，重新构建知识体系，将内化的知识外显，应用到其他情境中，感受习得知识的应用价值.

设置题目为原教学设计中题目2.

师生活动：连接AC，BD. 以点A为中心，将[△ACD]顺时针旋转60°或将[△ABD]逆时针旋转60°，均可构造等边三角形和直角三角形. 以点B，C为中心旋转亦可. 当学生发现以点[D]为中心旋转，线段无法集中导致问题无法解决时，教师及时指导. 让学生展示不同解法并互评. 教师与学生一起课堂小结.

预设成果：在高阶思维下解决问题，发展学生的几何直观这一核心素养. 联系此题的多种解法，回顾前面所学，反思辅助线作法，完善学生的个人认知体系.

修改后的上浮与应用阶段，较好地体现了通过元认知活动，对学习过程进行积极反思，促使学生真正获得知识的内核，即知识的意义，从而获得隐藏在知识里的促使人的思想、能力和价值发展的力量，提升学生应用知识解决问题的能力.

四、结束语

杜威提出的U型教学理论强调教学应该以学生为中心，重视知识的形成过程，以及学生认知的基本规律，将学生的学习过程分为下沉与还原、潜行与探究、上浮与应用三个阶段. 作为教师，应该充分解读课程标准，审视教学目标，帮助学生从“一型学习”走向“U型学习”，这需要教师利用U型模式对教学设计进行二次开发. 开发过程中结合深度学习的理念，还应关注以下三点.

1. 对标学科核心素养，提升教学设计站位

基于深度学习的课堂教学要求教师提升教学设计站位，以学科核心素养为导向，让学生在掌握知识技能、感悟知识本质的同时，形成批判性思维知识迁移和问题解决的能力，实现教育价值.

2. 提升认知结构的组织和再组织

在对教学设计进行二次开发时，教师要充分理解学生的认知特征，探索通过怎样的途径能够引发学生思考，从联系的角度引导学生研究新知识，注重归纳总结，将新知识概括到原有的认知结构中去.

3. 教学设计是一个动态过程，需要在实践的基础上不断修正和完善

在教学过程中，教师应学生动而动，应情境变而变，处理好预设和生成的关系，使学生逐步学会自主学习，从而实现“教是为了不教”的最终目标.

参考文献：

[1]刘月霞，郭华. 深度学习：走向核心素养[M]. 北京：教育科学出版社，2018.

[2]郭元祥. 论深度教学：源起、基础与理念[J]. 教育研究与实验，2017（3）： 1-11.

[3]安富海. 深度学习的课堂教学策略研究[J]. 课程·教材·教法，2014，34（11）： 57-62.

[4]谢虎成. U型模式：素养导向下的生物学课堂教学设计改进[J]. 中学生物教学，2020（3）： 18-21.