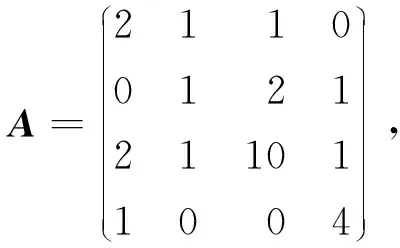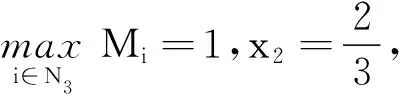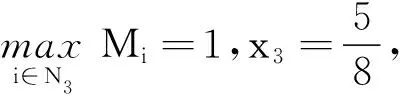关于非奇异H-矩阵判定的一组新的充分条件*
蒋雯雯,庹 清
(吉首大学数学与统计学院,湖南 吉首 416000)
非奇异H-矩阵是很重要的矩阵类,它在数学、物理和神经网络等领域的地位十分重要.在实际应用中,一个线性方程组的系数矩阵若是非奇异H-矩阵,则该方程组对Jacobi,Gauss-seidel,SOR等经典算法是收敛的,且该方程组有稳定解.所以,当判定大型线性方程组是否具有稳定解时,通常需要先判定其系数矩阵是否为非奇异H-矩阵.非奇异H-矩阵判定问题一直是数值计算研究中的热点.近年来,有学者给出了一些实用的判定条件[1-9].笔者将通过构造新的正对角矩阵,得到一组新的关于非奇异H-矩阵判定的充分条件.
1 基础知识
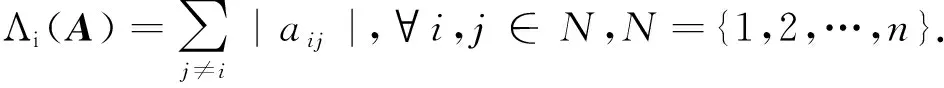
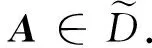
定义2[6]设A∈Mn(C)为不可约矩阵,若|aii|≥Λi(A)(∀i∈N),且其中至少有1个严格不等式成立,则A为不可约对角占优矩阵.
定义3[6]设A∈Mn(C),若|aii|≥Λi(A)(∀i∈N),且其中至少有1个严格不等式成立,又对每个等式成立的下标i,都存在非零元素链aij1aj1j2…ajk-1jk≠0,使得|ajkjk|>Λjk(A),则称A为具有非零元素链对角占优矩阵.
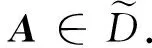
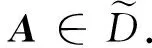

记
N1={i∈N|0<|aii|=Λi(A)},N2={i∈N|0<|aii|<Λi(A)},
N3={i∈N||aii|>Λi(A)},N=N1⊕N2⊕N3.
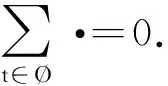
引理4[2]设A∈Mn(C),若对于∀i∈N2,有
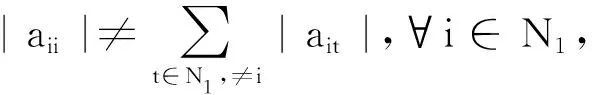
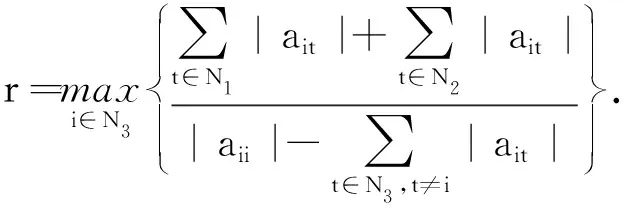
引理5[1]设A∈Mn(C),若对于∀i∈N2,有
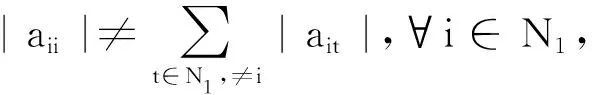
引理5是引理4的改进.
2 主要结果及其证明
记

定理1设A∈Mn(C),若
(1)
且对于∀i∈N1,存在t∈N3,使得ait≠0,则A是非奇异H-矩阵.
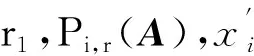
从而r1|aii|≥Pi,r(A)(∀i∈N3).因为0 由h的定义式变形可得 (2) 对于∀i∈N2,根据(1)式,可令 (3) 构造正对角矩阵D=diag(d1,d2,…,dn),记B=AD=(bij),其中 (2)对于∀i∈N2,由(3)式有 (3)对于∀i∈N3,由(2)式有 综上所述,|bii|-Λi(B)>0(∀i∈N),所以B是严格对角占优矩阵,从而A是非奇异H-矩阵. 注2因为 定理2设A∈Mn(C),且A不可约,若 (4) 且其中至少有1个严格不等式成立,则A是非奇异H-矩阵. 证明因为A是不可约矩阵,所以对于∀i∈k⊂N,j∈k/N,|aij|不全为0.构造正对角矩阵D=diag(d1,d2,…,dn),记B=AD=(bij),其中 (2)对于∀i∈N2,由(4)式有 (3)对于∀i∈N3,由(2)式有 综上所述,|bii|≥Λi(B)(∀i∈N).由于(4)式中至少有1个严格不等式成立,即至少存在1个i0,使得|bi0i0|>Λi0(B)(∀i0∈N).因为B=AD,A是不可约的,所以B是不可约的.由定义3可知,B是不可约对角占优矩阵.又由引理1可知,A是非奇异H-矩阵. 同理,在满足非零元素链的情形下,有以下定理: 定理3设A∈Mn(C),若 且对于∀i∈N-K,存在非零元素链aii1ai1i2…aisi*,其中i≠i1,i1≠i2,…is≠i*,i*∈K,则A是非奇异H-矩阵. 例1设 易知N1={1},N2={2},N3={3,4},通过计算可得 根据定理1,有 由此可知矩阵A满足定理1的条件,从而A是非奇异H-矩阵. 这不满足引理5的条件,即不满足引理4的相关条件. 例2设 易知N1={1,2},N2={3},N3={4,5},通过计算可得 根据定理1,有 由此可知矩阵A满足定理1的条件,从而A是非奇异H-矩阵.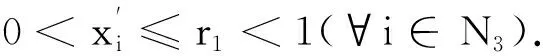





3 数值实例