一种用于射电天文图像重建的自适应尺度算法*

张 利，米立功，肖一凡，杨江河，李桂城,卫星奇，宁娜文，李丹杨，贺春林

(1.贵州大学大数据与信息工程学院，贵州 贵阳 550025；2. 黔南民族师范学院物理与电子科学学院，贵州 都匀 558000；3. 西华师范大学计算机学院，四川 南充 637002；4. 湖南文理学院 湖南 常德 415000)

射电干涉测量通过干涉技术能够获得等价于最长基线长度的阵列口径，这种测量技术大大提高了望远镜的分辨率.世界已经有很多著名的干涉阵，如甚大天线阵(VLA)、阿塔卡马大型毫米波/亚毫米波天线阵(ALMA)等.本世纪初以来，中国也加大对干涉阵的建设和资助力度，如已经运行的“宇宙第一缕曙光”探测项目(21CMA)和建设阶段的国际合作大项目——平方公里射电阵(SKA)等.这些望远镜阵都有很好的分辨率，能够有效分辨遥远的天体.然而很多干涉阵的点扩展函数(Point Spread Function, PSF)具有较高的旁瓣，因此移去点扩展函数的模型影响是有必要的.即使像SKA这种望远镜数量众多且设计优秀的望远镜阵，如果想要得到一个高动态范围的图像，反卷积重建仍然是必要的.

1 基本问题

Van Citter-Zernike理论[1]指出，可见度函数Vt与天体图像It存在傅里叶变换关系.由于测量是在空间频率域进行的，因此噪声也在空间频率域.测量的可见度函数Vm可以表示成

Vm=M(Vt+n0).

(1)

其中，n0为空间频率域噪声，M为采样函数.M属于非笛卡尔采样，在数据处理中，会重新采样到笛卡尔坐标系中.它的值为0或1，0代表未采样的点，1代表采样的点.由于望远镜的地理位置、观测源的位置和观测时间等一系列原因，一般情况下，会有大量的点测量不到.数据重建就是通过一些方法来估计出这些测量不到的空间频率.在空间域，测量的可见度函数Vm和采样函数M分别对应脏图Id和点扩展函数(脏束)B的傅里叶反变换.由卷积理论知道，脏图是点扩展函数与天体图像和噪声的卷积，即

Id=It*B+n*B，

(2)

式中，*表示卷积运算.未采样的频率在空间上对应“不可见分布”[1].如果p对应采样频率所对应的分布，那么p*B=0.如果Ii是卷积等式(2)的解，那么Ii+kp也是这个方程的解.因为k是任意的，所以有无数多个解满足卷积方程(2).数据重建的目的是找到一个最合理的“不可见分布”.

2 常用算法及其问题

目前有许多用于射电干涉图像重建的算法，如最大熵算法[2-3]、CLEAN算法[4-8]、压缩感知重建算法[9-11]等.其中一些基于函数模型分解的算法被广泛使用，如CLEAN算法.基于函数模型分解的算法主要有两大类：基于无尺度(Delta)函数模型分解的算法[4-8]和基于尺度函数模型分解的算法[12-13].基于Delta函数模型分解的算法擅长于处理致密源，而基于尺度函数模型分解的算法则更擅长于处理延展源.基于尺度函数模型分解的算法也能处理致密源，所以这类算法的性能常常要优于基于Delta函数模型分解的算法.非常典型的基于尺度函数模型分解的算法有2种：多尺度CLEAN算法[12]和自适应尺度像素分解算法[13].多尺度CLEAN算法基于球体波函数的分解，使用匹配滤波技术来寻找一个合适的分量.由于技术的限制，函数的尺度仅有几个，且这几个尺度是用户指定的，在重建过程中无法修改，所有的分量将被分解到这几个固定的分量；因此图像分量的尺度是无法确定的，需要更多的尺度来逼近潜在的真实图像.同时，多尺度CLEAN算法有预计算过程，预计算有较高的内存要求，如果图像过大或使用太多的尺度，可能会因内存不足而造成计算失败.自适应尺度像素分解算法是基于高斯函数的分解，使用非线性最优方法来实现尺度的自适应，很好地解决了多尺度CLEAN算法因固定尺度所带来的问题，有非常好的图像重建效果.同时，自适应尺度像素分解算法追求更加稀疏的分解，所以重复使用非线性最优方法来优化前面所得到的参数.然而尽管使用了加速的方法，这种算法的计算量还是非常大，以至于没有写入软件中.因此，设计一种新的算法以平衡计算的复杂度和性能，具有重要的意义.

3 自适应尺度重建算法

为了解决计算复杂度和性能的平衡问题，笔者提出了一种新的反卷积重建算法.算法基于自适应尺度高斯函数的分解，使用Levenberg-Marquardt非线性最优方法[14]来实现尺度的自适应能力.这种二阶的非线性最优方法也保证了模型分量的最优.对于每一个模型分量，算法需要最优化目标函数

(3)

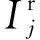
(4)

其中，f(x,y;p)是高斯函数，g是循环增益.该算法中截断的高斯函数被使用，这有效地解决了高斯函数支撑集太大的问题.算法的基本过程为：

Step 1 匹配滤波找到一个合适的尺度和位置；

Step 2 使用非线性优化方法进行高斯函数拟合，找到最优解；

Step 3 更新最优解到模型；

Step 4 计算残差；

Step 5 满足最大迭代次数或达到噪声水平时停止.

自适应尺度重建算法被设计用于栅格化的数据，然而测量的射电干涉数据并不在栅格点上，需要很多的运算来进行数据栅格化.因此结合CLEAN框架，通过使用CLEAN算法的主循环(Major Cycle)，有效利用成图(Imaging)部分的算法，如卷积插值和重采样等，使算法能处理非栅格化的直接测量数据，也能有效地纠正一些小循环中产生的误差[1].该算法可以在CLEAN框架里作为次循环(Minor Cycle)，主要为了找到最优的模型，具体流程如图1所示.

图1 基于自适应尺度重建算法重建图像的流程Fig. 1 Diagram of Reconstruction Algorithm Based on Adaptive Scale

与自适应尺度像素分解算法一样，自适应尺度重建算法也使用了非线性最优方法来优化模型分量；所不同的是，自适应尺度像素分解算法重复地优化前面已经优化的参数，而自适应尺度重建算法不再重复优化前面已得到的参数，大大减少了算法的计算复杂度.相比于多尺度CLEAN算法，自适应尺度重建算法的尺度是自适应的，能够有效解决固定尺度分解所带来的问题.同时，该算法没有多尺度CLEAN算法的预计算步骤，可有效地解决多尺度CLEAN算法的内存开销问题.

4 数值模拟

自适应尺度重建算法可应用于非栅格化数据.数据利用通用天文软件程序包(Common Astronomy Software Applications, CASA)来模拟，使用VLA的B阵型在L波段模拟观测到的射电源M31，模拟的观测数据格式和真实的观测数据格式是相同的，测量的量也是一致的.相对于真实数据，模拟得到的数据更加完善，模拟的数据相当于校准之后的真实观测数据.对于测试图像重建算法而言，与使用真实数据的函数有同样的效果.笔者使用残差图像的均方根误差(Root Mean Square Error, RMSE)和动态范围(Dynamic Range, DR)[15]比较了自适应尺度重建算法和Högbom CLEAN算法及多尺度CLEAN算法.Högbom CLEAN算法和多尺度CLEAN算法是在射电干涉天文图像处理中常用的两种算法，分别是基于Delta函数分解的反卷积算法代表和基于多尺度函数分解的反卷积算法代表.

残差图像的均方根误差能够有效地表示残差的水平，均方根误差越小，说明残差水平越低，图像中的信息被恢复越多.残差图像的均方根误差

(5)

其中，N是图像的像素点数，‖·‖ln是ln范数.

动态范围是天文图像处理中常用的判断图像质量的依据，越高的动态范围意味着图像更好地被重建.动态范围被定义为重建图像的最大值与残差图像的非源区域的均方根误差之比，即

(6)

其中，Ire表示重建的图像，RMSEp表示残差图像的非源区域的均方根误差.

本数值模拟实验所处理的射电源M31图像原图及其点扩展函数图像和脏图如图2所示.

图2 自适应尺度重建算法所处理的M31图像Fig. 2 M31 Image Processed by Improved Algorithm

从图2(a)可以看出，射电源M31是一个非常复杂的源，包含了大量子结构，能有效地测试各重建算法的性能.采集到的数据表明，射电源M31点扩展函数(图2(b))的最大负旁瓣是-0.068 7.从图2(b)可以看出，旁瓣结果复杂且分布很广.被点扩展函数模糊化之后的脏图为图2(c).测试图像原图的大小为512×512像素，为了使显示更加清晰便于比较，成图仅显示处理结果的中央256×256像素部分.

在成图过程中所有算法均使用Robust加权函数.Robust加权函数能够有效抑制旁瓣水平，是一种常用的加权函数.Högbom CLEAN算法使用的参数是：迭代次数30 000，循环增益0.1.多尺度CLEAN算法使用的参数是：迭代次数10 000，循环增益0.3，尺度分别为0，4，12，36，108像素.自适应尺度重建算法使用的参数是：迭代次数7 000，循环增益0.7.由于自适应尺度重建算法是基于自适应尺度的，所以不需要用户指定尺度.各算法的处理结果如图3所示.

图3 典型CLEAN算法与自适应尺度重建算法的结果对比Fig. 3 Comparison of Results from Typical CLEAN Algorithm and the Improved Algorithm

从图3(a)中可以看出，Högbom CLEAN算法重建的模型图像由点组成，这是由于Högbom CLEAN算法是基于Delta函数分解的，即图像被分解为Delta函数集合.Delta函数集合是通过找到残差图像中的最大绝对值点，然后乘以循环增益得到Delta函数的位置和系数.这种分解不能有效地表示延展结构，所以使用这类算法处理延展源时，残差图像中会残留“平台”式的相关结构，而且需要大量的分量来表示图像.从这个测试中可以看出，尽管Högbom CLEAN算法使用了远大于其他两种基于尺度函数分解的算法的迭代次数，然而结果却是最差的.多尺度CLEAN算法使用了几个尺度函数来表示图像，较好地解决了基于Delta函数模型的算法不能有效表示图像的问题.从图3(b)也能看出，相对于Högbom CLEAN算法，多尺度CLEAN算法重建的模型图像更加接近于真实图像，残差图像中所留下的相关结构也更小(图3(e)).然而基于多尺度函数模型分解的算法将图像强行分解到仅有的尺度当中，这需要更多的分量来表示图像.基于自适应尺度函数模型的算法能有效地解决这一问题，使用更少的分量来表示图像.从图3(c)中可以看出，相对于Högbom CLEAN算法和多尺度CLEAN算法，笔者提出的自适应尺度重建算法模型图像更加接近于真实图像.残差图像(图3(f))也能有效证明这一结论.图3还表明，在这三种算法中，自适应尺度重建算法的残差相关结构是最少的，说明自适应尺度函数模型能够更好地表示图像.表1列出三种算法重建图像的RMSE和DR数值结果.

表1 三种方法重建结果的数值比较

从表1可以看出，在这三种算法中，自适应尺度重建算法有最小的残差均方根误差和最高的动态范围，进一步说明自适应尺度重建算法的性能优于基于Delta函数模型算法和基于多尺度函数模型算法.

5 结语

多尺度CLEAN算法是一种基于多尺度函数模型的重建算法，广泛应用于射电干涉天文图像的重建，但是由于尺度是固定的，内存消耗严重，因此不宜处理大图像.自适应尺度像素分解算法利用非线性最优化使尺度具有自适应能力，解决了固定尺度不能有效表示延展结构问题，图像质量较多尺度CLEAN算法有很大提升.然而由于该算法重复优化前面已经优化了的参数，尽管每一分量更加准确，但是计算量却大大增加，以致无法写入软件中.笔者提出了一种改进的自适应尺度重建算法，不再重复地优化前面已经优化了的参数，后面的优化会纠正前面优化的不准确性.自适应尺度重建算法是基于CASA和Python编程实现的，为了能够处理非栅格化数据，将自适应尺度重建算法与CLEAN框架相结合，计算的复杂度较自适应尺度像素分解算法大大减少，重建结果优于基于多尺度函数模型算法.