二维磁场中的随机Bénard问题解的适定性*

谢 婷

(南京财经大学应用数学学院，江苏 南京 210046)

1 问题的提出

考察二维磁场中的Bénard问题[1]：

∂tu+(u·)u+π-Δu=(b·)b+θe2,

∂tb+(u·)b-Δb=(b·)u,

∂tθ+(u·)θ-Δθ=ue2,divu=divb=0,

(u,b,θ)(x,0)=(u0,b0,θ0)(x)x∈R2.

其中：u为流体速度场；b为磁场；θ为温度；π为修正后的压力；e2=(0,1)T.有学者[2-6]研究了磁场中的Bénard问题的全局正则性和非线性稳定性的充要条件，磁场中带有混合偏粘度、局部耗散的二维Bénard问题的适定性、正则性，以及有界域上的一致全局解.

考虑随机乘法噪声的影响：

(1)

(2)

(3)

divu=divb=0,

(4)

(u,b,θ)(x,0)=(u0,b0,θ0)(x)x∈R2.

(5)

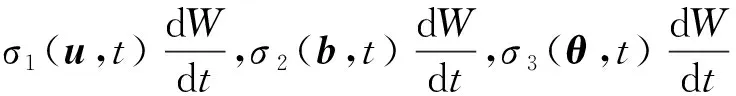
笔者将讨论二维磁场中的随机Bénard问题弱解的存在唯一性，并在此基础上研究二维磁场中的随机Bénard问题解的正则性.

2 预备知识

令

它是完备的、可测的函数，其中

u∈{u|u∈L2,·u=0}，b∈{b|b∈L2,·b=0}.

定义1[7]定义Λ=(-Δ)1/2，其中

‖Λh(fg)-fΛhg‖Lp≤M(‖f‖Lp1‖Λh-1g‖Lq1+‖Λhf‖Lp2‖g‖Lq2).

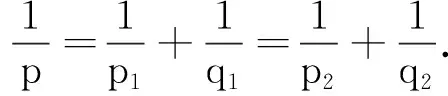
则当X∈L∞([0,T]×Ω)时，对于∀t∈[0,T]，有

假设

(6)

(7)

(8)

3 主要结果及其证明

(u,b,θ)∈L2(Ω,C(0,T);L2)∩L2(Ω,L2(0,T);H1).

(9)

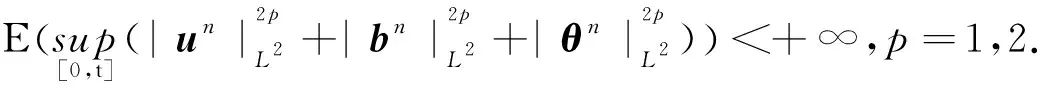
则

(10)

由Burkholder-Davis-Gundy不等式可得

(11)

由(6)，(10)，(11)式可得

(12)

则

(13)

由Burkholder-Davis-Gundy不等式可得

(14)

由(7)，(13)，(14)式可得

(15)

则

(16)

由Burkholder-Davis-Gundy不等式可得

(17)

由(8)，(16)，(17)式可得

(18)

由(12)，(15)，(18)可得

于是

‖(un,bn,θn)‖L2(Ω,C(0,T);L2)+‖(un,bn,θn)‖L2(Ω,L2(0,T);H1)≤M.

(19)

则

(20)

由Burkholder-Davis-Gundy不等式可得

(21)

由(6)，(20)，(21)式可得

(22)

则

(23)

由Burkholder-Davis-Gundy不等式可得

(24)

由(7)，(23)，(24)式可得

(25)

则

(26)

由Burkholder-Davis-Gundy不等式可得

(27)

由(8)，(26)，(27)式可得

(28)

由(22)，(25)，(28)式可得

即

再由(19)式可得

(29)

(ⅱ)单调性.

引理2[9]若(1)～(5)式中所有非线性项相加之和B(w)满足

则单调性成立.

对于∀u1,u2,b1,b2,θ1,θ2且u1≠u2,b1≠b2,θ1≠θ2，有

(uλ,bλ,θλ)∈L2(Ω,C(0,T);L2)∩L2(Ω,L2(0,T);H1)λ=1,2.

(a)

〈(u1·)u1-(u2·)u2,u1-u2〉=-〈(u1·)u1,u2〉-〈(u2·)u2,u1〉=

-〈((u1-u2)·)(u1-u2),u2〉,

则

|〈(u1·)u1-(u2·)u2,u1-u2〉|=|〈((u1-u2)·)(u1-u2),u2〉|≤|u1-u2|L4·

(30)

(b)

〈(u1·)b1-(u2·)b2,b1-b2〉=-〈(u1·)b1,b2〉-〈(u2·)b2,b1〉=

-〈((u1-u2)·)(b1-b2),b2〉,

则

|〈(u1·)b1-(u2·)b2,b1-b2〉|=|〈((u1-u2)·)(b1-b2),b2〉|≤|u1-u2|L4·

(31)

(c)

〈(u1·)θ1-(u2·)θ2,θ1-θ2〉=-〈(u1·)θ1,θ2〉-〈(u2·)θ2,θ1〉=

-〈((u1-u2)·)(θ1-θ2),θ2〉,

则

|〈(u1·)θ1-(u2·)θ2,θ1-θ2〉|=|〈((u1-u2)·)(θ1-θ2),θ2〉|≤|u1-u2|L4·

(32)

(d)

〈(b1·)b1-(b2·)b2,u1-u2〉+〈(b1·)u1-(b2·)u2,b1-b2〉=〈(b2·)u1,b2〉-

〈(b1·)u1,b2〉+〈(b1·)u2,b1〉-〈(b2·)u2,b1〉=〈((b2-b1)·)u1,b2〉+

〈((b1-b2)·)u2,b1〉≤|b2-b1|L4‖u1‖|b2|L4+|b1-b2|L4‖u2‖|b1|L4≤

(33)

再由(19),(29)式和引理2可知单调性成立.

综上可知，(1)～(5)式有唯一弱解(u,b,θ)满足(9)式.

(34)

(35)

(36)

由(6)，(7)，(8)，(34)，(35)，(36)式和文献[10]可得

则

(37)

令

则由(37)式可得

即

E(I(t))≤βE(X(t))+γE(Y(t)).

2(1+M1eM1)E(Z)<+∞，

于是

‖(u,b,θ)‖L2(Ω,C(0,T);H1)+‖(u,b,θ)‖L2(Ω,L2(0,T);H2)≤M.

(38)

下面估计‖Λh(fg)-fΛhg‖Lp≤M(‖f‖Lp1‖Λh-1g‖Lq1+‖Λhf‖Lp2‖g‖Lq2)，其中

(39)

(40)

由(6)，(7)，(39)，(40)式和文献[10]可得

则

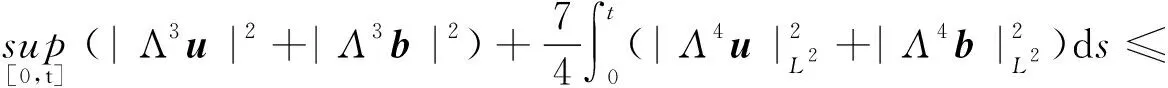
(41)

令

则由(41)式可得

即

E(I(t))≤βE(X(t))+γE(Y(t)).

于是

‖(u,b)‖L2(Ω,C(0.T);H3)+‖(u,b)‖L2(Ω,L2(0,T);H4)≤M.

4 结语

笔者证明了二维磁场中的随机Bénard问题存在唯一弱解，并对二维磁场中的随机Bénard问题解的正则性进行了探讨.这对进一步研究随机的Bénard问题的稳定性、遍历性和偏差准则具有重要意义.