基于PPSO算法的电力系统无功优化*

王 琳

(东北大学信息科学与工程学院，辽宁 沈阳 110004)

随着社会的发展，电负荷的种类和数量越来越多，而且具有随机性的分布式电源大量并入电网，使得电力系统的电源分布和网络结构发生改变[1]，导致网络内无功分布不合理，影响电能质量，尤其影响电压质量.因此，如何降低损耗、提高电力系统输电效率和保证电力系统经济运行，已经成为电力系统运行部门主要考虑的问题[2].电力系统无功优化的原则是，在满足约束条件下通过调节发电机电压、电压器分接头和无功补偿设备，给出一套合理的配置方案，从而达到所要求的目标[3].

无功优化的优化方法主要包括常规优化方法和智能优化算法.线性规划法[4]、非线性规划法[5]和简化动态规划法[6]等常规优化方法都存在处理离散变量困难的情况.近些年，有学者采用智能优化算法解决无功优化问题，如遗传算法(Genetic Algorithm, GA)[7]、禁忌搜索算法(Taboo Search Algorithm, TSA)[8]和粒子群优化(Particle Swarm Optimization, PSO)算法[9]等.GA程序简便、寻优能力较强，但优化时间较长；TSA耗时少，但对初值敏感，若超出禁忌表的长度则可能迂回搜索；PSO算法易于实现，鲁棒性好，但易陷入局部最优.针对PSO算法存在的不足，有学者提出随机惯性权重粒子群优化(Random Inter Weight Particle Swarm Optimization, RIPSO)算法[10]和改进吸引排斥粒子群优化(A New Diversity Guided Particle Swarm Optimizer, ATRE-PSO)算法[11]，但这些算法都无法进一步提高精度.基于此，笔者将采用向量粒子群优化(Phasor Particle Swarm Optimization, PPSO)算法[12]求解电力系统无功优化问题，通过引入相位角来改进速度更新公式，并在IEEE-14节点系统中进行仿真实验，以验证PPSO算法求解电力系统无功优化问题的可行性.

1 无功优化数学模型

电力系统无功优化问题是一个多目标、多约束和多变量的非线性动态规划问题[13].一般优化问题的数学模型为

minf(x,u)

(1)

其中：f为目标函数;g为等式约束所代表的函数；h为不等式约束所代表的函数；hmin为不等式约束的最小值；hmax为不等式约束的最大值；x为状态变量；u为控制变量.在电力系统无功优化问题中，控制变量可分为连续控制变量和离散控制变量，发电机电压属于连续控制变量，电压器分接头位置和无功补偿设备的容量则属于离散控制变量.

无功优化的目标是有功损耗最小，其目标函数为

(2)

其中：Ui和Uj分别为节点i，j处的电压幅值；Gij为节点i，j之间的电导；θij为节点i，j之间的电压相位角之差.等式约束条件为

其中：Pi和Qi分别为节点i处注入的有功功率和无功功率；QGi为节点i处无功补偿设备提供的无功功率；PDi和QDi分别为节点i处负荷消耗的有功功率和无功功率；Bij为节点i，j之间的电纳.不等式约束条件为

其中：Uimin和Uimax分别为节点i处的电压幅值的最小值和最大值；Qimin和Qimax分别为节点i处注入的无功功率的最小值和最大值；QGimin和QGimax分别为节点i处无功补偿设备提供的无功功率的最小值和最大值；Pimin和Pimax分别为节点i处注入的有功功率的最小值和最大值；Timin和Timax分别为第i台变压器分接头变比的最小值和最大值.

2 基于向量粒子群优化算法的无功优化

2.1 向量粒子群优化算法

PPSO算法在粒子初始化问题上不同于一般的粒子群算法.n个粒子在M维的空间中由如下公式随机生成：

Xi=|Xi|<θii=1,…,n，

(3)

(4)

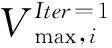
(5)

其中Xmax,m和Xmin,m分别为第i个粒子的位置最大值和最小值.

PPSO算法在速度和位置更新上，也与一般的粒子群算法不同.PPSO算法的速度和位置的更新公式分别为

(6)

(7)

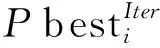
(8)

(9)

2.2 优化步骤

采用PPSO算法求解电力系统无功优化问题的步骤如下：

(ⅰ)将网络线路参数、发电机参数、控制变量参数和PPSO算法相关参数等输入仿真系统.

(ⅱ)以发电机电压、无功补偿设备容量和变压器分接头作为控制变量，建立解空间，在不超过上下限的前提下随机取值，并组成n个M维粒子.由模型(1)可知，控制变量个数即粒子的维度M.根据(3)～(5)式计算相关参数.

(ⅲ)根据(2)式计算各个粒子在配电网络中的有功损耗，并判断计算结果是否满足所有等式约束和不等式约束，若不满足任意一条约束，则重新初始化不满足条件的粒子.

(ⅳ)速度更新采用(6)式，位置更新采用(7)式.

(ⅴ)根据(2)式计算更新后的粒子的有功损耗.

(ⅶ)向量角更新采用(8)式，速度最大值更新采用(9)式.

(ⅷ)重复步骤(ⅳ)—(ⅶ)，直至满足最大迭代次数为止.

3 仿真验证

3.1 IEEE-14节点系统

以IEEE-14节点系统作为仿真系统.该系统由14个节点(其中节点9为并联补偿电容器节点)、20条支路、5台发电机和3台可调变压器组成，其网络结构如图1所示.

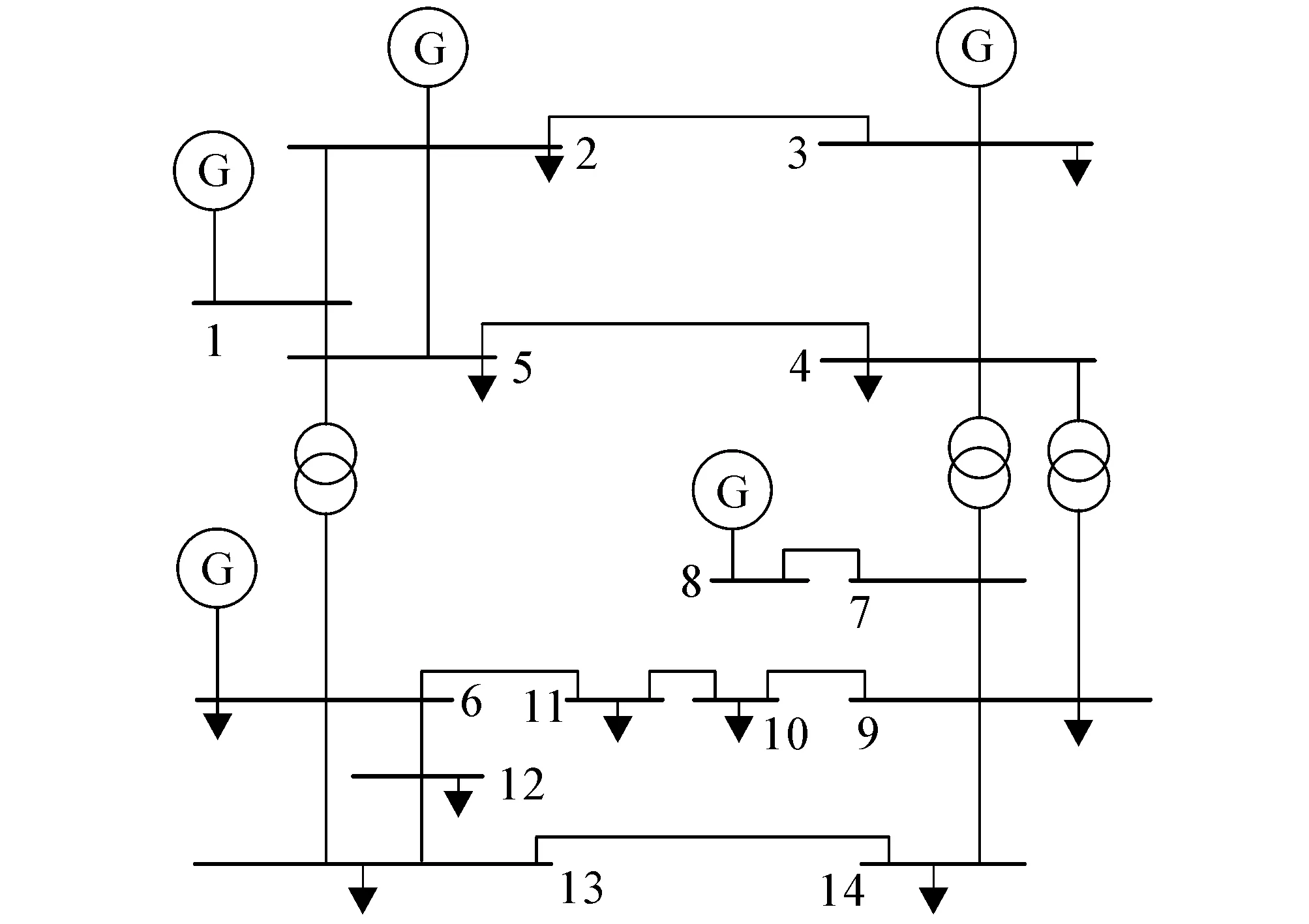
图1 IEEE-14节点的网络结构Fig. 1 Structure Diagram of IEEE-14 Node Network

IEEE-14节点系统中，发电机电压的可调区间为0.90～1.10 p.u.；可调变压器变比的可调区间为0.90～1.10 p.u.，步长为0.02 p.u.，共有11个接头；并联电容器电纳的上限为0.5 p.u.，步长为0.05 p.u.，共有10组.文献[14]中详细地给出了其他关于IEEE-14节点系统的参数.

3.2 无功优化仿真实验

在IEEE-14节点系统中，利用PPSO算法与标准粒子群优化(Standard Particle Swarm Optimization, SPSO)算法[15]、RIPSO算法、ATRE-PSO算法进行无功优化仿真实验.取粒子数为40，迭代次数为100，维数为9，潮流计算采用牛顿拉夫逊法，以节点1作为平衡节点.为了减小随机性，每种算法运行30次.运行30次得到的结果的平均值见表1.

表1 有功损耗优化结果

由表1可知，优化算法都能降低有功损耗，算法不同，其有功损耗也不同.与SPSO算法、RIPSO算法和ATRE-PSO算法相比，PPSO算法的有功损耗最小值分别降低1.121 4，0.036 2，0.993 7 MW，这说明PPSO算法的有功损耗最小，且能更有效地跳出局部最优解.4种算法的有功损耗最小值收敛曲线如图2所示.

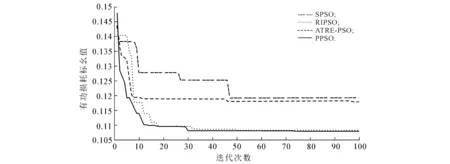
图2 有功损耗最小值收敛曲线Fig. 2 Convergence Curve of Minimum Active Power Loss

由图2可以看出，PPSO算法在收敛精度和收敛速度方面都有较好的表现.静态特性上，PPSO算法最终得到的有功损耗小于其他算法；动态性能上，由于PPSO算法对速度最大值进行了更新，加快了粒子速度收敛的效率，因此相比其他3种算法，它的收敛速度更快.

4 结语

建立了有功损耗最小目标优化函数，采用PPSO算法在IEEE-14节点系统中进行无功优化仿真实验.仿真结果表明，相比SPSO算法、RIPSO算法和ATRE-PSO算法，PPSO算法能更有效地降低有功损耗，加快收敛速度，且更有效地跳出局部最优解.这充分说明在求解电力系统无功优化问题上，PPSO算法是有效且可行的.在接下来的研究方向中，可以引入分布式电源，考虑含分布式电源的电力系统无功优化问题；也可以对PPSO算法作一定的改进，进一步提高算法的收敛速度和收敛精度；还可以使用不同的优化目标函数，为多目标无功优化问题作准备.