含有教育和科技进步因素的经济模型*

王 珊，王 锋

(萍乡学院数学系，江西 萍乡 337000)

实践证明，区域经济与教育紧密相关，促进经济与教育协调发展，合理投入人力资本和实物资本，对社会的可持续发展具有重要意义[1].关于经济与教育的关系，国内外学者对其做了很多研究[2-8].其中，Steinmann等[2]构建了一个含有教育的经济模型，得到经济的长期发展和逃出马尔萨斯陷阱的可能性都依赖于科技进步的结论.但这个经济模型中基于Cobb-Douglas生产函数的经济表达式是规模报酬不变的，而根据参数的不同取值，生产函数可分为3种类型，即规模报酬递增型、规模报酬递减型和规模报酬不变型.因此，笔者将利用微分动力系统理论模型研究在更一般情形下的经济发展动态.

1 基础知识

(1)若μ>0且Δ=τ2-4μ≥0，则系统以原点为结点.当τ<0时，结点为稳定结点；当τ>0时，结点为不稳定结点.

(2)若μ>0且Δ=τ2-4μ<0，τ≠0，则系统以原点为焦点.当τ<0时，焦点为稳定焦点；当τ>0时，焦点为不稳定焦点.

(3)若μ>0且τ=0，则系统以原点为中心.

(4)若μ<0，则系统以原点为鞍点.

2 模型的建立与分析

2.1 模型的建立

Steinmann等[2]构建了一个以实物资本K(t)、人力资本H(t)和科技进步W(t)为变量的人口经济模型，且假设这些变量随时间是连续变化的.设生产函数为

Y(t)=Hα(t)Kβ(t)Wγ(t)，

(1)

其中0<α≤1，0<β≤1，γ>0.根据Cobb-Douglas生产函数的分类：当α+β>1时，表示规模报酬递增；当α+β=1时，表示规模报酬不变；当α+β<1时，表示规模报酬递减.

假设人力资本分为受教育程度E(t)和人口数量L(t)这2个部分，满足

H(t)=Lε(t)E1-ε(t) 0<ε<1.

(2)

将(2)式代入(1)式，得到

Y=LεαE(1-ε)αKβWγ.

(3)

为了简便表达，(3)式省略了时间变量t.

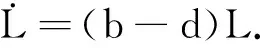
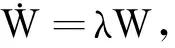
将L(t)和W(t)的值代入(3)式，得到生产函数关于受教育程度E(t)和实物资本K(t)的表达式

Y=(entL0)εαKβE(1-ε)α(eλtW0)γ=μ0e(nεα+λγ)tKβE(1-ε)α,

每个阶段需要从产出Y中对实物资本进行投资以促进社会不断发展.设其投资率为sK，则每个阶段实物资本K将增加sKY.但由于在使用中实物资本会出现一定的折旧和损耗，因此实物资本变化的动态方程可表示为

(4)

其中δ为实物资本折旧率.同样地，每个阶段需要对教育进行投资以促进社会更长远的发展.设其投资率为sE，则每个阶段受教育程度E将增加sEY.但由于人口的死亡会减少人力资源，也就会减少教育的存量，因此受教育程度变化的动态方程可表示为

(5)

于是，(4)，(5)式建立了如下的二维动力系统：

(6)

2.2 模型的分析

(7)

对方程组(7)中的两式分别求对数导数，得到

(8)

将(6)式代入(8)式，可将非自治微分动力系统转为如下形式的自治微分动力系统：

(9)

定理1二维微分动力系统(9)在K1，E1平面的第一象限存在唯一的非零平衡点.

(10)

(11)

显然，(0,0)为系统(9)的平凡均衡点，但是它对问题的研究没有实际意义，因此本研究中主要考虑非平凡平衡点.将(10)，(11)式移向并相除，得到

(12)

将(12)式代入(9)式，求得如下非零平衡点：

定理2当

1-(α+β)+εα>0

(13)

证明由1-(α+β)+εα>0，则p>0.设

则矩阵J的行列式值μ=(1-(α+β)+εα)(δ+p)(d+p)，迹τ=(β-1)(δ+p)+((1-ε)α-1)(d+p).由0<α<1，0<ε<1，0<δ<1，d>0，0<β≤1可知，μ>0,τ<0.再由

Δ=τ2-4μ=((β-1)(δ+p)+((1-ε)α-1)(d+p))2-4(1-(α+β)+εα)(δ+p)(d+p)=

((β-1)(δ+p))2+2(αβ-εα+α+β-βαε-1)(δ+p)(d+p)+((1-ε)α-1)2(d+p)2≥

((β-1)(δ+p))2+2(α-εα-1+β-1)(δ+p)(d+p)+((1-ε)α-1)2(d+p)2=

((β-1)(δ+p)+((1-ε)α-1)(d+p))2≥0，

注1当α+β=1(规模报酬不变)和α+β<1(规模报酬递减)时，(13)式满足，根据定理2，这2种情况中平衡点都为稳定结点.当规模报酬为递增的情况时，即α+β>1，且α+β-1<εα成立时，平衡点是稳定的.

(14)

对(14)式求导并取极限，得到

对Y=μ0exp((nεα+λγ)t)KβE(1-ε)α取对数，得到

lnY=lnμ0+(nεα+λγ)t+(1-ε)αlnE+βlnK，

故

3 数值模拟

现利用数值模拟探讨微分系统(9)在不同情形下的稳定性问题.令

α=0.6，γ=0.2，ε=0.6，b=0.1，d=0.05，λ=0.08，L0=2，W0=1，sK=0.3，sE=0.2，δ=0.08.

接下来就β的不同取值验证系统的稳定性.

情形1令β=0.3，初始值(K1,E1)=(0.5,3.4)，此时α+β<1，规模报酬递减，其轨迹如图1所示.

情形2令β=0.4，初始值(K1,E1)=(1,5)，此时α+β=1，规模报酬不变，其轨迹如图2所示.

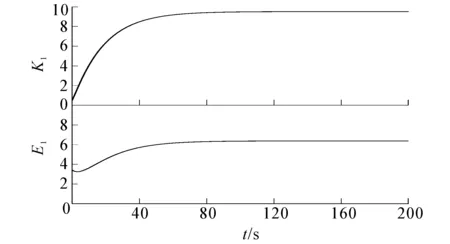
图1 情形1的轨迹Fig. 1 Trajectory of Case 1

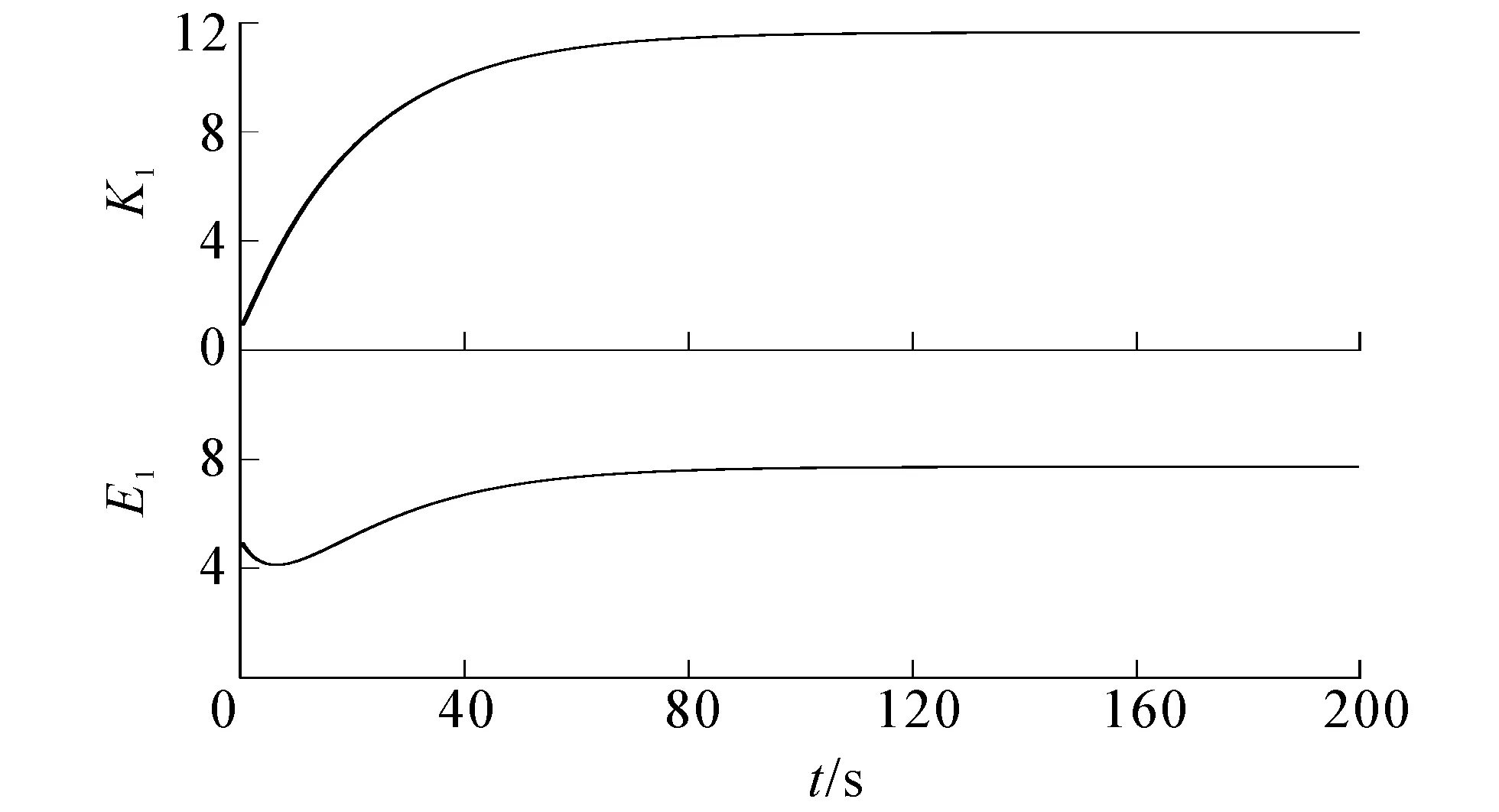
图2 情形2的轨迹Fig. 2 Trajectory of Case 2

情形3令β=0.55，初始值(K1,E1)=(2,6)，此时α+β>1，规模报酬递增，其轨迹如图3所示.

情形4令β=0.8，初始值(K1,E1)=(2,6)，此时不满足1-(α+β)+εα>0，K1,E1可能会不稳定，其轨迹如图4所示.

图3 情形3的轨迹Fig. 3 Trajectory of Case 3

图4 情形4的轨迹Fig. 4 Trajectory of Case 4

前3种情形中1-(α+β)+εα>0，满足定理2的条件，故平衡点是稳定的.从图1～3可以看出，随着时间的不断增长，K1,E1的轨迹将趋于稳定.从图4可以看出，K1,E1在有限时间内趋于无穷大.

4 结论