基于湿度扩散理论T梁非均匀收缩效应分析

张柳煜， 冯步文*， 陈汉斌， 王龙

(1.长安大学 陕西省公路桥梁与隧道重点实验室， 陕西 西安 710064； 2.云南省公路局道桥技术工程公司；3.昭通市宜毕高速公路投资开发有限公司)

近年来，随着T梁桥大规模建设，该类结构的典型病害也日益凸显。其中T梁腹板竖向裂缝更为突出，由于产生频繁，且开裂机理不明确，逐渐引起广大学者的关注。T梁腹板竖向开裂具有规律性，轻则深入腹板表面1～2 cm，重则贯穿腹板。由文献[1-3]可知,从常规力学角度不能够很好地解释该类裂缝的成因，对典型病害产生机理阐述过于宽泛，以经验结论居多，多归咎于结构施工质量，混凝土材料收缩温度等作用。不能定性定量说明各种作用对结构的实际影响。

混凝土收缩徐变是混凝土材料的重要特性。随着时间的推移，收缩徐变会导致结构产生次效应，引起结构内力重分布，是混凝土结构开裂的重要影响因素之一。目前常用的混凝土材料收缩徐变预测模型有CEB-FIP、GL2000、B3、ACI等。桥梁结构计算过程中，结合常用杆系结构分析方法，以结构构件理论厚度、环境湿度、混凝土强度为指标，对结构的收缩徐变效应进行分析。但难以考虑由于截面各部位差异产生的不均匀收缩效应；文献[6-9]均采用不同混凝土预测模型对连续梁桥不均匀收缩效应进行分析，认为该效应对主梁挠度具有重要影响；文献[10]、[11]通过公式推导对T梁不均匀收缩效应进行分析，认为不均匀收缩效应是腹板开裂的影响因素之一。但现有混凝土收缩预测模型存在较多假定，影响参数单一，主要用于预测混凝土收缩效应对结构整体的影响，较难真实反映主梁不均匀收缩效应。

基于湿度扩散理论的混凝土收缩变形分析方法可有效计算混凝土构件非均匀收缩效应。文献[12]、[13] 对混凝土自身与干燥收缩一体化问题、混凝土早期及在干湿环境下内部湿度分布及变化规律、混凝土结构非线性收缩应力的计算等问题进行了试验与理论研究；文献[14]、[15]通过试验及湿度扩散理论对连续刚构桥由于不均匀收缩产生的变形进行了分析，分析结果得出：混凝土箱梁非均匀收缩效应对连续刚构桥变形具有显著影响。

该文主要以混凝土湿度扩散理论为基础，计算T梁结构非均匀收缩效应，研究T梁三维湿度场分布规律及时变特征。并在不同影响因素下，针对混凝土T梁腹板竖向开裂影响因素进行研究。

1 混凝土湿度扩散理论

混凝土的收缩是其自身的重要特性。多年来，国内外大量学者对混凝土收缩效应做出了大量研究和探索，得出了大量有益的研究成果。近年来，由于高强度混凝土开裂现象普遍，混凝土收缩现象被进一步关注。同时由于失水导致的混凝土收缩机理进一步被揭示，混凝土由于湿度驱动而产生收缩的变形分析也得到进一步探索，使得混凝土收缩效应可以进行定性、定量的精细化分析。

1.1 混凝土湿度场计算方法

初始水分布、水泥水化消耗水分(混凝土自身收缩)、水分扩散(混凝土干燥收缩)是混凝土内湿度变化的3个主要原因。湿度场计算与温度场计算类似，普遍认为，混凝土湿度场分布满足Fick定律：

(1)

式中：H为混凝土内相对湿度；t为时间；D为湿度扩散系数；qd为湿度自消耗函数。

通常采用有线差分法和有限元法进行混凝土内湿度场求解。由于湿度场计算与温度场计算方程、边界及初始条件具有极大的相似性，随着有限元的发展，通常采用通用有限元程序中温度场计算模块对混凝土构件湿度场进行模拟。文献[16]、[17]对模拟过程进行了详细阐述，在此不再赘述。

1.2 有限元分析参数取值

(1) 湿度扩散系数

湿度扩散系数是混凝土湿度场计算过程中的重要参数，不同的测量方法，不同的回归分析方法，得到的湿度扩散系数计算模型均存在较大的不同。根据大量研究可知：混凝土湿度扩散系数在混凝土整个湿度扩散过程中不是常量，与混凝土内部相对湿度存在较大的联系。随着时间的推移，混凝土内部水化程度加深，水泥石变得更加密实，湿度扩散系数逐渐降低。该文参考CEB-FIP推荐公式，即：

(2)

式中：Dsat为混凝土内部相对湿度100%时的湿度扩散系数，其取值范围：Dsat=1×10-6～1×10-5m2/h；hc为D=0.5Dsat时相对湿度；其余值为试验常数，缺少实测值时，CEB-FIP 90推荐参数：α0=0.05，hc=0.8，n=15。

(2) 湿度交换系数

湿度交换系数hf用来描述混凝土表面湿度与空气湿度的传递速率。交换系数与混凝土表面状况有直接联系，表面粗糙程度、空气温度、相对湿度、相对温度、风速等都对该值存在较大影响，此外，不同混凝土配比，也对该值有较大贡献。

(3) 混凝土水分自消耗函数

在混凝土水化过程中，由于水化反应的进行，混凝土内部水分随时间逐渐消耗，但混凝土长期收缩变形过程中，混凝土自身收缩占总体收缩比例较小，为10%～20%，且早期发展较快。根据文献[17]、[18]，该文取混凝土水分自耗率函数为:

(3)

式中：h∞为与混凝土水灰比相关的函数，取值范围为-0.5～0；Kz为常数，取值范围为0～0.02 h-1；nn为指数，与混凝土养护条件有关，一般取1.2。

(4) 干湿变形系数

文献[12]、[13]、[19]、[20]研究表明：混凝土内部湿度变化是混凝土收缩特性的驱动力。随着时间的推移，混凝土内部湿度逐渐降低，混凝土体积发生变化，从而产生混凝土收缩效应。不同学者提出不同的结构湿度变形与湿度的耦合关系，一般地，混凝土内部湿度的改变量与结构变形间关系呈非线性，其函数表达为：

(4)

三维湿度场计算属于求解三维非线性对流扩散方程的初边值问题。根据有关参考文献计算时近似认为混凝土干湿变形系数为常量。预应力混凝土T梁采用C50混凝土，根据文献[17]相关混凝土试验，计算参数取值如表1所示。

2 预应力混凝土T梁非均匀收缩效应分析

2.1 模型概况

取30 m预应力混凝土T梁桥一片中梁为分析对象。截面梁高200 cm，两侧翼板厚18 cm，腹板厚为20 cm。计算过程中考虑桥面10 cm现浇混凝土铺装层对T梁结构湿度场分布的影响，并假定30 d时完成现浇混凝土铺装层。通过表1中各参数建立湿度场有限元分析模型，分析混凝土浇筑后10年T梁内湿度场分布及变化规律。有限元模型如图1、2所示。其中S1、Z1、Z2、X1为计算结果选择的特征点。其中S1点为T梁顶板特征点，反映T梁顶板湿度及应力变化规律，Z1、Z2为T梁腹板特征点，反映T梁腹板表面及内部的湿度及应力变化规律，X1为马蹄特征点，反映马蹄内部湿度及应力变化规律。

表1 有限元计算参数取值

图1 T梁普通钢筋模型

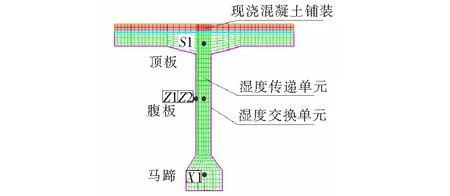
图2 跨中截面有限元模型

2.2 混凝土湿度场分析

混凝土湿度场计算为瞬态问题，计算过程中采用欧拉向后积分法。通过建立上述有限元模型， 对比分析不同参数下，T梁混凝土湿度场随时间的分布情况。以700 d为例，T梁湿度分布如图3所示。

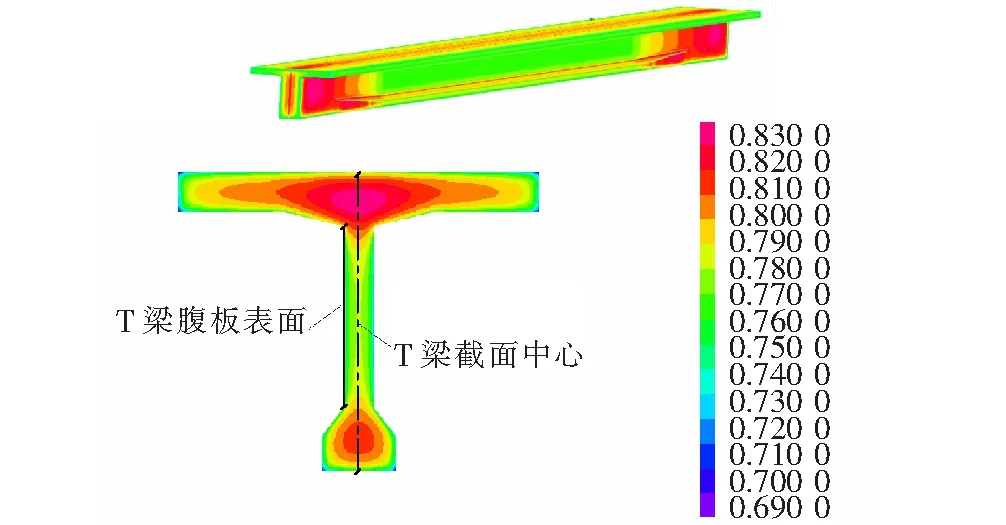
图3 700 d时混凝土湿度场分布

根据图3可知：T梁湿度分布存在较大的不均匀性，梁端腹板较厚，混凝土内水分散失较慢，跨中腹板较薄，水分散失较快；由于T梁顶板、腹板、马蹄尺寸的差异，湿度分布也存在较大差异，从截面中心比较，腹板水分散失最快，从腹板横向比较，腹板表面水分散失最快。

(1) 考虑混凝土水分自消耗对湿度场分布的影响(图4、5)由图4可知：由于T梁各部分厚度不同，混凝土湿度分布不同，腹板湿度下降最快，明显快于顶板及马蹄；现浇层混凝土浇筑后，经短暂时间和顶板混凝土湿度扩散后湿度呈均匀分布。由图4、5可知：水分自消耗对混凝土湿度分布总体影响较小，浇筑早期的影响大于后期。

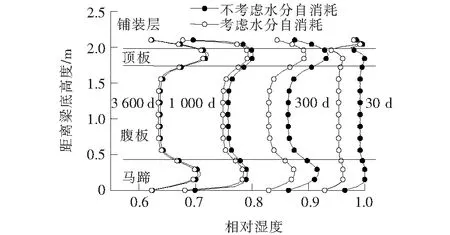
图4 T梁截面中心相对湿度随高度变化(考虑自消耗)

图5 不同特征点处相对湿度随时间变化(考虑自消耗)

(2) 不同湿度交换系数对湿度场分布的影响

湿度交换系数对混凝土内水分的消耗有着重要贡献。取hf=1×10-5、1×10-4m/h两种不同湿度交换系数对T梁混凝土湿度场分布进行分析。结果如图6、7所示。

由图6、7可知：不同湿度交换系数对T梁湿度分布有显著影响。由于湿度交换系数不同，混凝土腹板表面(Z1点)变化最剧烈，时间为300 d左右时，较高湿度扩散系数工况该点湿度已接近平均环境湿度0.6，而较低扩散系数工况仍保持较高的0.78。由于交换系数增大，混凝土内水分散失加快，早期湿度梯度增大，混凝土更快达到环境湿度。

图6 T梁截面中心相对湿度随高度变化(考虑hf变化)

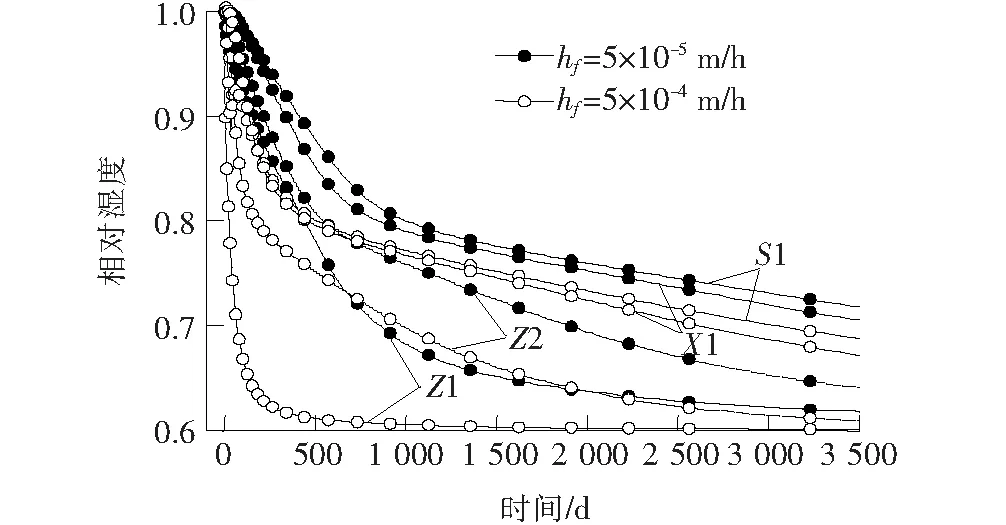
图7 不同位置相对湿度随时间变化(考虑hf变化)

2.3 结构湿度变形应力分析

根据湿度场与结构场间耦合关系，建立T梁结构场计算模型，进行结构应力分析。计算过程中取干湿变形系数为常数，考虑不同湿度交换系数对结构应力分布的影响及普通钢筋对T梁不均匀收缩的影响。

(1) 湿度交换系数对结构应力的影响

根据上述分析可知，湿度交换系数的取值对T梁内湿度分布影响较大，取不同湿度交换系数下结构应力进行分析。分析过程中假定混凝土为均匀弹性材料，并取压应力为负值，拉应力值为正值。结果如图8、9所示。

图8 T梁截面应力随高度变化(考虑hf变化)

由图8、9可知：T梁内应力分布与湿度场分布相似，存在不均匀性。预应力T梁由于非均匀收缩产生较高次应力，其中，顶板与马蹄以受压为主(-3～-4 MPa)， 腹板表面以受拉为主(4～9 MPa)。由于湿度交换系数不同，混凝土表面水分散失速率不同，湿度梯度间存在较大差异。当湿度交换系数较大时，早期湿度梯度明显较大，应力峰值出现时间较早(200～300 d)，计算拉应力峰值较大(9 MPa)；当湿度交换系数较小时，应力峰值出现时间推后(1 000～1 200 d)，计算拉应力峰值明显减小(4.5 MPa)。通过降低混凝土表面粗糙程度，将混凝土振捣密实等措施来改善混凝土湿度交换系数，可降低非均匀收缩效应。

图9 不同位置应力随时间变化(考虑hf变化)

(2) 普通钢筋对结构应力分布的影响

根据30 mT形梁上部构造通用图可知：顶板、腹板、马蹄配筋率分别为0.92%、0.28%、3.23%。由于T梁不同部位配筋率不同，普通钢筋对混凝土收缩发展具有约束作用，截面内部仍然会导致混凝土不均匀收缩而产生自收缩应力。计算时取湿度交换系数hf=1×10-4m/h。计算结果如图10、11所示。

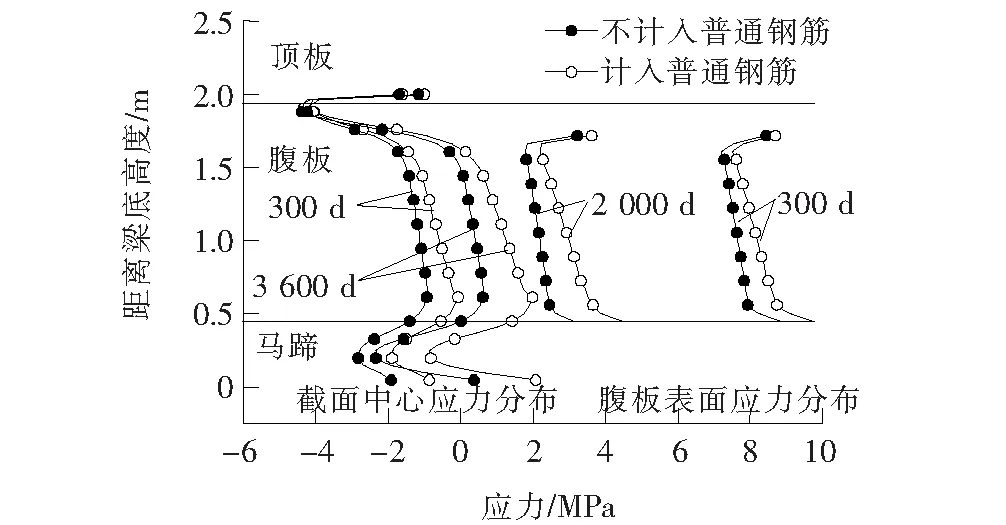
图10 T梁截面应力随高度变化(考虑普通钢筋)

由图10、11可知：普通钢筋对混凝土收缩存在一定的约束作用，由于各部位配筋率不同，其交界部位将产生额外的约束应力。对于腹板(Z1、Z2点)，由于普通钢筋的约束，随着时间变化，表面计算拉应力逐渐大于不考虑普通钢筋工况，最终差值达0.9 MPa(3 600 d)。相反，对于顶板及马蹄(S1、X1点)由于普通钢筋的约束作用，两部位压应力逐渐低于不考虑普通钢筋工况，最终差值达1.6和0.3 MPa(3 600 d)。

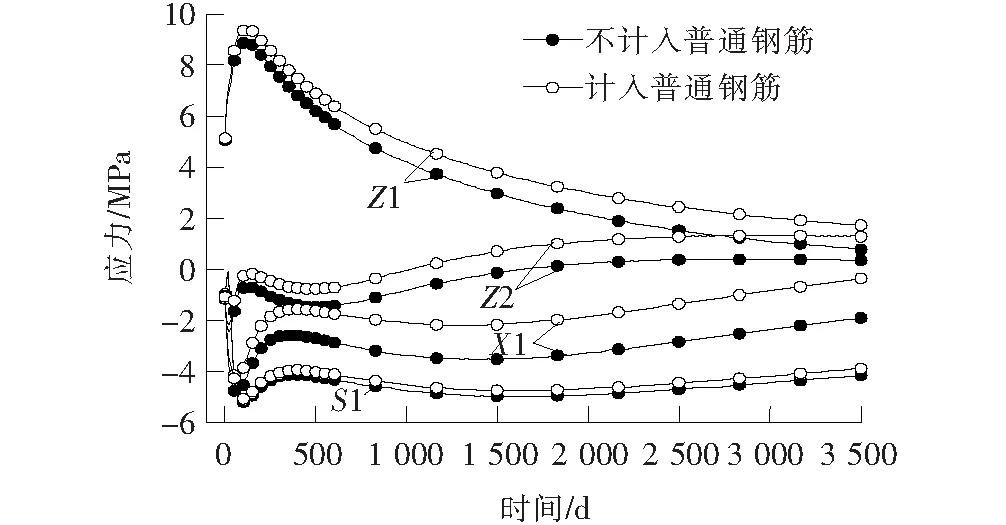
图11 不同位置应力随时间变化(考虑普通钢筋)

3 结论

基于湿度扩散理论，通过建立湿度场及结构场耦合模型，对混凝土T梁三维湿度场分布及变化规律进行了分析，并以湿度场分布为基础，对混凝土T梁由于混凝土不均匀收缩效应进行了分析，可得如下结论：

(1) T梁内部湿度分布存在不均匀性。T梁梁端腹板较厚，跨中腹板较薄，梁端干燥速率低于跨中；由于T梁顶板、腹板、马蹄尺寸存在差异，干燥速率存在差异，腹板干燥最快。

(2) 混凝土水分自消耗对T梁长期湿度场分布影响较小；表面湿度交换系数影响较大。

(3) 根据湿度场分布不均匀性，T梁截面存在较明显的不均匀收缩效应。T梁顶板及马蹄由于不均匀收缩呈受压状态，腹板呈部分受拉状态，其中腹板表面存在较高拉应力，开裂风险较高，将导致腹板竖向开裂。

(4) 湿度交换系数对T梁应力峰值的大小及出现时间均存在较大影响，通过加强混凝土振捣、增加混凝土密实性、降低混凝土腹板表面粗糙度等措施可有效改善T梁非均匀收缩产生的次应力。

(5) 由于T梁各部位配筋率不同，普通钢筋对混凝土非均匀收缩的约束作用使T梁产生约束应力，该约束效应对腹板有不利影响。