青藏工程走廊冻融土热扩散系数特性与预测模型研究

刘志云， 钟振涛， 崔福庆， 陈建兵， 彭 惠

（1.长安大学地质工程与测绘学院，陕西西安710054； 2.中交第一公路勘察设计研究院有限公司高寒高海拔地区道路工程安全与健康国家重点实验室，陕西西安710075）

0 引言

青藏工程走廊作为最重要的陆路进出藏通道，穿越了约550 km 多年冻土区，特殊的工程地质条件引发了冻胀、融沉、开裂、拥包、塌陷及不均匀变形等病害［1-2］。在未来的青藏高速公路工程建设中，高速公路黑色沥青路面特有的强烈吸热、聚热效应将给路基下伏冻土带来更大的热冲击［3］，诱发更为严重的工程病害［4-5］。如何保障这一特殊工程场景下公路工程的安全性和稳定性，是寒区冻土工程研究重要课题之一［6］。热扩散系数是表征土体内温度扩散速率的物理量，反映了传热过程中导热系数和比热容两大基础参数协同作用的效果［7］。同时，冻土的热扩散系数一定程度上也是冻土本身对外部热量输入响应敏感性的重要标尺，是描述多年冻土特征的关键参数之一［8］。因此，揭示多年冻土热扩散系数的变化规律、提出适用的预测模型对于未来青藏高速的设计施工和病害防治具有重要意义。

热扩散系数主要获取方法有理论计算和试验测试，其中理论计算是基于土壤为常热扩散系数的半无界介质假设，以一维热传导方程为理论基础获得计算公式，主要包括振幅法、相位法、对数法、反正切法、数值法和谐波法等［9-10］。许多研究者针对不同计算方法进行了对比分析，Horton 等［11］从计算所需数据条件和计算结果方面对比评价了六种热扩散系数计算方法，发现具有显式方程的振幅、相位、反正切和对数方法所需地温数据少，但计算结果偏差大，而以隐式求解的数值法和谐波法通常以大量实测地温为计算基础，结果更为可靠。缪育聪等［12］根据现场观测地温数据计算了地表浅层5～20 cm 土壤层的热扩散系数，对比发现充分利用实测地温信息的谐波法为最优估算方法。韩炳宏等［13］对青海南部高寒草地土壤的热扩散系数进行了计算，研究表明热传导对流法计算结果及其拟合效果最好，同时发现除干土层外随土壤深度加深，热扩散系数逐渐递减。同时，不少学者根据土壤的传热特征对计算方法进行了修正，Gao 等［14-16］综合考虑了土壤热传输过程中的热传导和多孔热对流方式，给出了一维热传导对流方程，采用谐波法和拉普拉斯变换方法推导了热传导对流方程的解析解及热扩散系数的计算公式，并基于实测地温数据验证了改进方法的准确性和优越性。原黎明等［17］基于改进的热传导对流方法对青藏高原中部活动层表层下5～20 cm 深度的土壤热扩散系数进行了估算，结果发现5～10 cm 处土壤热扩散系数显著大于10～20 cm 深度，且融化季对应热扩散系数显著高于冻结季。章永辉等［18］基于青藏高原理塘区野外观测地温数据，研究发现利用耦合热传导-对流法计算所得热扩散系数模拟地温时的准确性最高。在试验方面，甄作林等［19］利用瞬态平面热源法测试了原状和重塑砂土的热扩散系数，分析发现热扩散系数与干密度成正比关系，而含水率低时热扩散系数与含水率为正相关性，达到一定含水率时热扩散系数趋于稳定或与其呈负相关性。

关于热扩散系数影响因素方面，研究主要集中于土壤质地、内部结构、含水率、温度及深度等。王可里等［20］通过对青藏高原那曲地区非均质土壤热扩散系数计算发现，热扩散系数分布具有明显的深度和季节性变化特征，且冷暖季采用不同热扩散系数可获得较好地温模拟效果。周亚等［21］根据青藏高原观测站长期监测所得0.8 m 和3.2 m 深度土壤温度，给出了青藏高原不同地区深层土壤热扩散系数的年际和季节性变化特征。刘经星等［22］利用数值差分求解方法对不同质地条件土壤的热扩散系数进行了估算，结果发现土壤质地轻且土熵条件好对应热扩散系数小。Roxy［23］、安可栋等［24］根据观测数据研究了土壤水分和热扩散系数之间关系，研究表明热扩散系数随土壤水分增加先增大后减小。邸佳颖等［25］通过室内试验对比研究了原状土和装填土的热特性差异，结果表明装填土在处于中等含水率时热扩散系数较原状土有所增大，而接近饱和时热扩散系数趋于一致。马欣等［26］研究发现土壤热扩散系数与深度为非线性正相关性，且降水增多会降低热扩散系数。在计算模型方面，Arkhangelskaya 等［27］以土壤质地、容重和有机碳百分含量作为影响变量，建立了不同土类任意含水率状态下的热扩散系数回归模型。

但应看到的是，目前冻土热扩散系数的研究报道还相对较少，缺乏针对青藏工程走廊带典型类别土样热扩散系数的大规模测试与预测模型研究。为了进一步揭示青藏工程走廊带沿线多年冻土的热物理性质，本文基于青藏公路改扩建（格尔木—拉萨段）工程地质勘察项目912 组土样导热系数测试结果和质量加权法计算获取的比热容理论值，计算获得西大滩—唐古拉山沿线典型类别土样热扩散系数，分析了冻融土热扩散系数的分布特征和参数影响规律，提出了基于经验拟合公式法和RBF 神经网络方法的冻融土热扩散系数预测模型，并对不同预测模型的预测效果进行了对比分析，以期为青藏高速公路的热工设计提供数据参考。

1 热扩散系数计算方法

热扩散系数定义为导热系数与体积比热的比值，是反映物体增温快慢的综合物性参数，计算公式如下：

式中：α为土壤热扩散系数；λ为土壤导热系数，W·m-1·K-1；C为体积比热，kJ·m-3·K-1。

本文青藏工程走廊重塑冻融土导热系数采用Hot Disk TPS1500 热常数分析仪以瞬态平面热源法进行测试，其中测试区段北起西大滩（即走廊带多年冻土北界）南至唐古拉山共437 km，对应青藏公路里程桩号为K2870～K3307。钻孔取样深度自地表向下最深达40 m，共计获取土样912组，其中测试融土样633组、冻土样858组。

对钻探获取的土样进行土性统计，将土样数超过15 组的列为典型土样，按照土的工程分类，可将走廊带内所取土样分为黏性土、粉土、全风化岩类、砂土和碎石土共计5 大类12 个亚类，各土类统计如图1所示。由图可知，走廊带内主要以黏性土为主，砂土和碎石土次之，且二者数量相近。

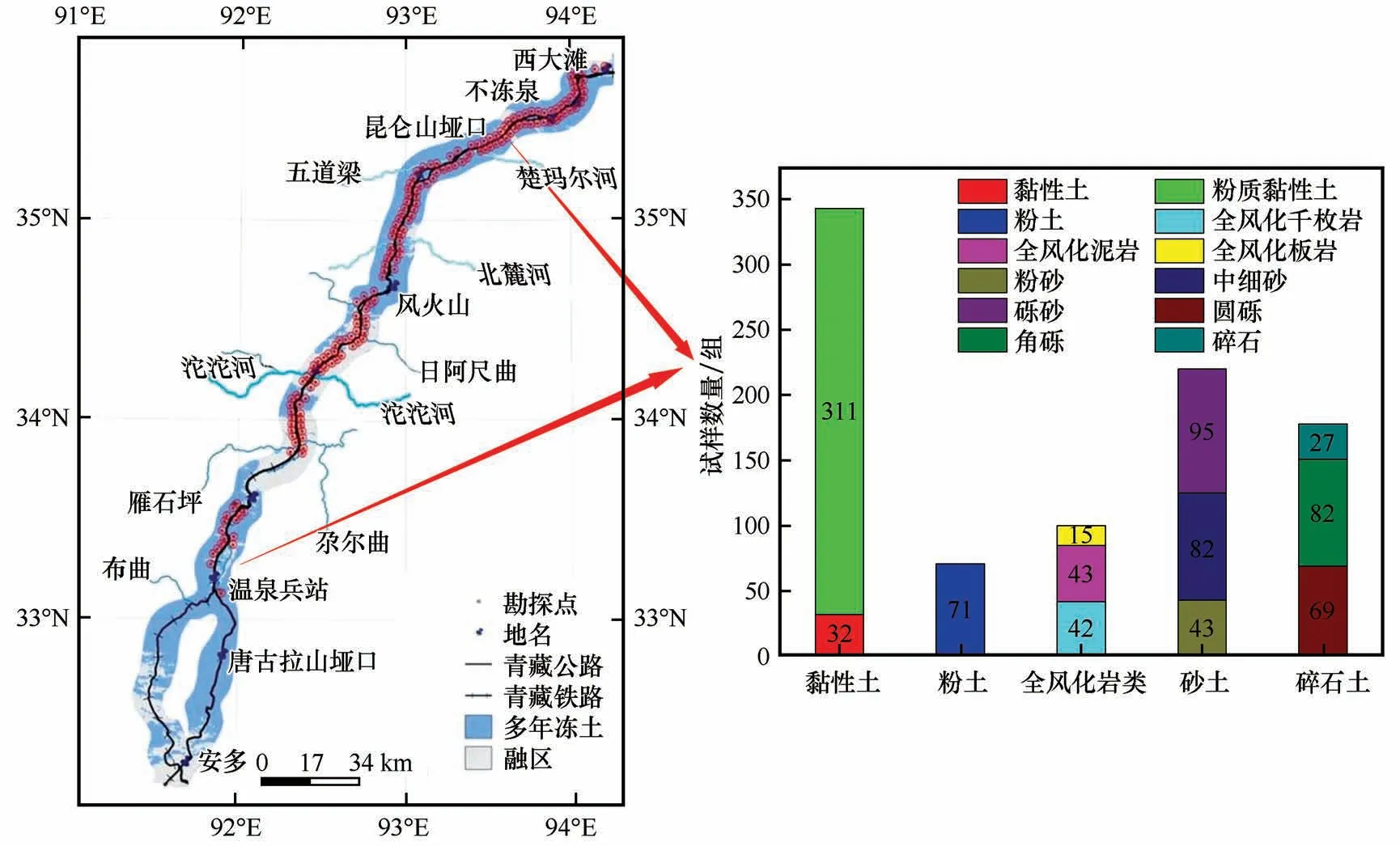
图1 青藏工程走廊导热系数测试区段及土性分布Fig.1 Thermal conductivity test section and soil property distribution of Qinghai-Tibet engineering corridor

导热系数测试主要操作包括：（1）试样制备：土样烘干筛分、增湿至天然含水率、静置闷样及加压制样；（2）测试预处理：平整试样表面和预先冻结冻土试样；（3）物性测试：确定测试时间及功率、重复测试和数据误差对比。其中试样制备依据《土工试验方法标准》（GB/T50123—2019）规范内容进行，具体测试系统如图2所示。

图2 导热系数测试系统Fig.2 Thermal conductivity test system

体积比热按照文献［28］所给公式进行计算，该研究认为土比热是多相组分的质量加权平均结果，冻融土比热因固态冰的存在具有明显差异，具体计算式如下：

式中：Cu和Cf分别为融土和冻土的体积热容量，kJ·m-3·K-1；Csu、Csf、Cw和Ci分别为融土骨架、冻土骨架、水及冰的质量比热，kJ·kg-1·K-1；W和Wu分别为总含水量和未冻水含量；ρu和ρf分别为融土和冻土的天然密度，kg·m-3。其中不同土类冻融土骨架及水分质量比热取值见表1所示。

表1 不同土类土骨架及水质量比热取值Table 1 Mass specific heat of soil skeleton and water for different soil types

2 冻融土热扩散系数分布特征及影响因素分析

2.1 冻融土热扩散系数分布特征

对五类土热扩散系数进行统计，得到其概率分布如图3 所示。由图3 可知，融土热扩散系数主要分布区间整体依黏性土、粉土、全风化岩类、砂土和碎石土偏右分布，表明融土热扩散系数主要分布范围值依次增大。可以看出，土的成分对融土的热扩散系数有显著影响，粒径越小，土的持水性越强，则结合水的比例越高，降低了水分在矿物骨架之间的联系作用，从而导致其热扩散系数降低。为排除由取样随机性带来的统计误差，取累积概率分布区间20%～80%热扩散系数为对比值，统计得黏性土、粉土、全风化岩类、砂土和碎石土融土热扩散系数分布区间为0.441×10-6～0.595×10-6、0.485×10-6～0.694×10-6、 0.486×10-6～0.677×10-6、0.589×10-6～0.829×10-6和0.653×10-6～0.858×10-6m2·s-1，均值分别为0.507、0.565、0.586、0.699 和0.759×10-6m2·s-1。可以看到，走廊带内各土类融土热扩散系数与粒径呈正相关性，分布基本排序为黏性土、粉土、全风化岩类、砂土及碎石土依次增大。

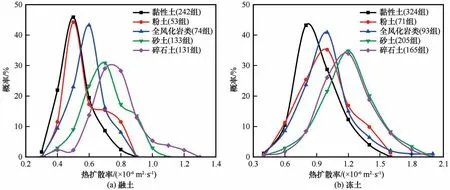
图3 土类热扩散系数概率分布Fig.3 Probability distribution of thermal diffusivity of soils

同理，图3 中各土类冻土热扩散系数主要分布区间整体按黏性土、全风化岩类、粉土、碎石土和砂土依次增大，其累积概率分布区间20%～80%对应的 热 扩 散 系 数 区 间 为0.742×10-6～1.057×10-6、0.826×10-6～1.134×10-6、0.810×10-6～1.213×10-6、0.996×10-6～1.374×10-6和0.998×10-6～1.410×10-6m2·s-1，均值 分 别 为0.882×10-6、0.976×10-6、0.985×10-6、1.172×10-6和1.194×10-6m2·s-1。对比发现，各土类冻融土热扩散系数分布规律不尽相同，可能与水分冻结引发土体结构变化有关，总体来说，走廊带内土类冻土热扩散系数分布基本排序为黏性土、全风化岩类、粉土、碎石土及砂土依次增大。

对比各土类冻土与融土热扩散系数发现，冻土热扩散系数均显著大于融土，其中黏性土、粉土、全风化岩类、砂土和碎石土均值相对增幅分别为73.96%、74.34%、66.55%、70.82%和54.41%，这是因为冻结状态下土体内水变为冰后具有更强的导热能力和较小的比热。同时，还可发现粒径较小土类整体具有较大相对增幅，可能与土体冻结过程土骨架结构连接性增强相关，粒径较小土类表现出更大增幅的导温性。

2.2 土体天然含水率、干密度对热扩散系数的影响

对走廊带内冻融土热扩散系数与天然含水率、干密度之间的偏相关性进行统计分析，结果如表2所示。由表可知，黏性土、粉土和碎石土冻融土热扩散系数与干密度呈显著的正相关关系，这是因为含水率不变的情况下，其质量比热也不变，而导热系数随干密度变大而增大，故随着干密度变大其冻融土热扩散系数相应增大。但也存在全风化岩类冻融土及砂土冻土热扩散系数与干密度为负相关性情况，由图4可知，在自然环境状况下不同干密度条件对应热扩散系数分布随机且离散，并不具有较强的正相关性。

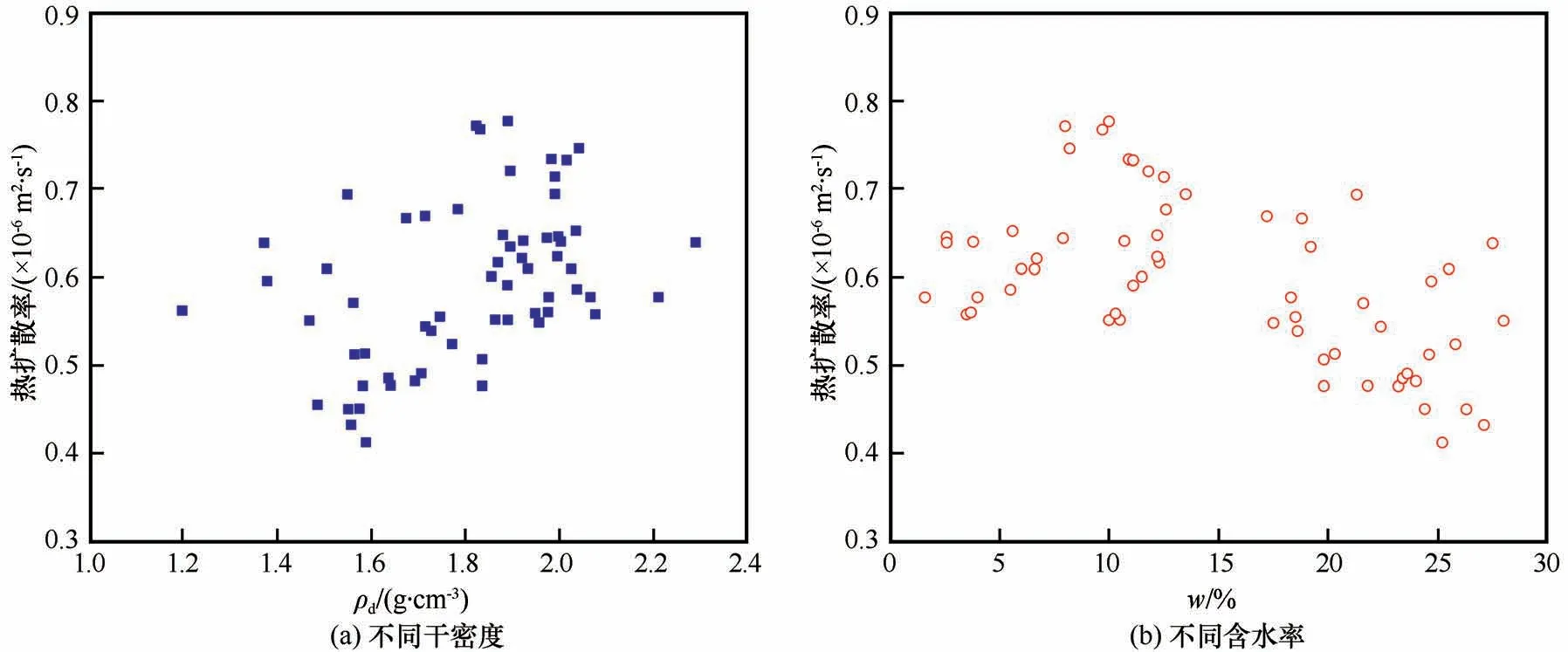
图4 全风化岩类融土热扩散系数与干密度及天然含水率分布关系Fig.4 Relationship between thermal diffusivity and dry density and natural water content distribution of unfrozen soil of fully weathered rocks

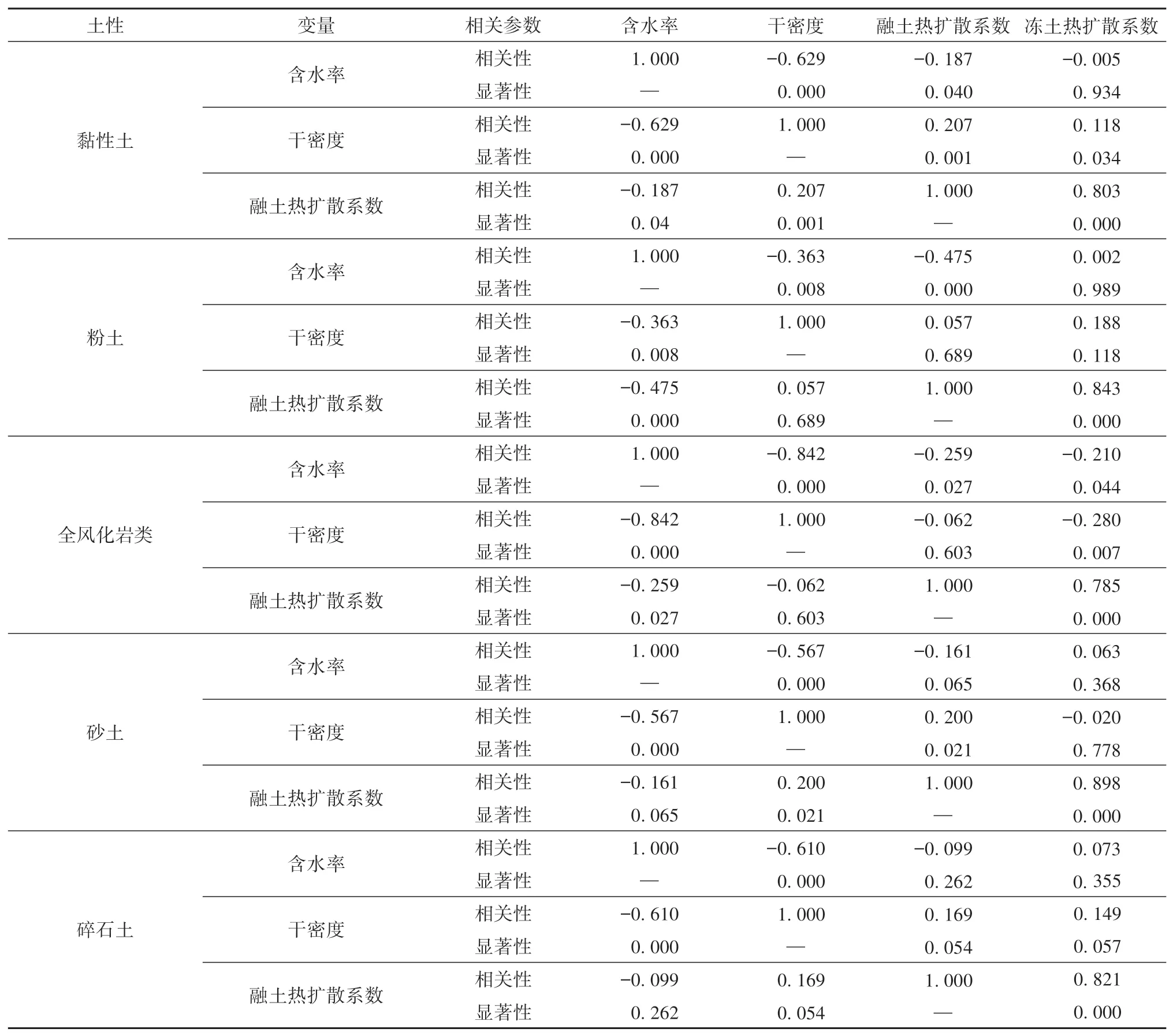
表2 热扩散系数与影响因素偏相关分析Table 2 Partial correlation analysis between thermal diffusivity and influencing factors

同时，可发现各土类冻融土热扩散系数与含水率间关系差异显著，大部分土类热扩散系数与含水率呈负相关性，但粉土、砂土及碎石土冻土热扩散系数与含水率呈正相关性，同样如图3所示，这可能与天然条件下土类处于不同赋水状态时，热扩散系数随含水率变化规律不同相关。此外，还可发现土体天然含水率与其干密度有强烈的负相关性，冻融土热扩散系数之间具有显著正线性相关性。

3 冻融土热扩散系数预测

3.1 冻融土热扩散系数预测模型

3.1.1 二元拟合

对走廊带内冻融土热扩散系数与干密度、天然含水率之间的拟合关系进行曲线估计后发现，基本都呈为多项式函数形式，得到走廊带内冻融土热扩散系数一般拟合公式如下：

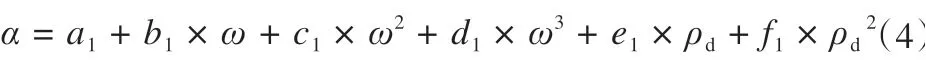
式中：α为土体热扩散系数，10-6m2·s-1；ω为天然含水率，%；ρd为干密度，g·m-3；a1、b1、c1、d1、e1和f1均为待定的拟合系数，各土类拟合值见表3所示。

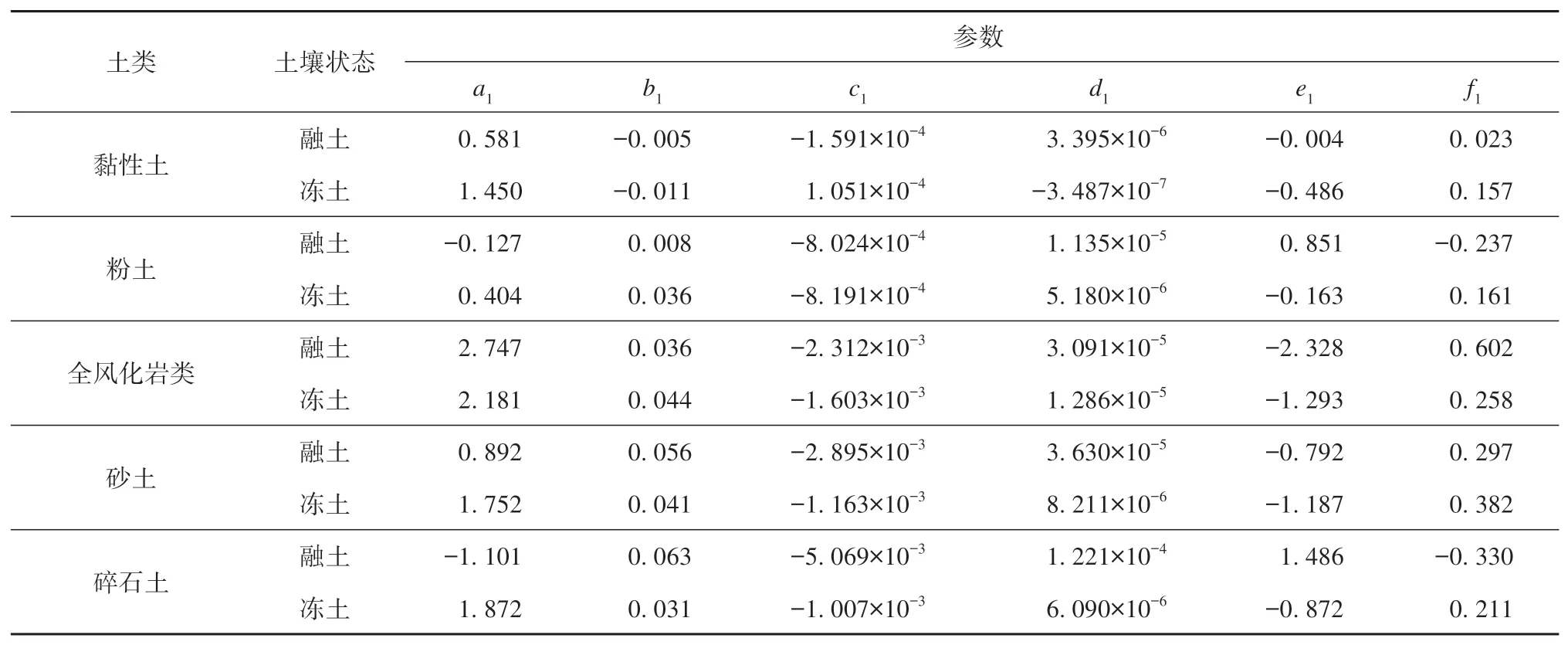
表3 热扩散系数二元拟合相关参数Table 3 Related parameters of binary fitting for thermal diffusivity

3.1.2 基于融土热扩散系数的冻土三元拟合

青藏高原走廊带内土类分布多样且分散，各土类矿物成分及组分粒径等分布界限并不一定明显，土类间存在相互混杂现象，所以简单将其分类后采用干密度和含水率对其热扩散系数进行预测会产生一定偏差。此外，相对于冻土而言，融土试样制备及测试更为简单，且融土热扩散系数结果隐含有决定土性成分和粒径等信息，前述偏相关分析表明二者具有极强的正线性相关性，同时考虑干密度、含水率对冻土热扩散系数预测结果进行修正，得到走廊带内冻土热扩散系数的三元拟合公式如下：

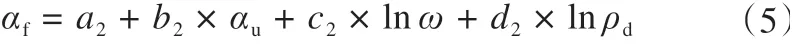
式中：αf和αu分别为冻土和融土热扩散系数，10-6m2·s-1；a2、b2、c2和d2均为待定的拟合系数，各土类拟合结果见表4所示。

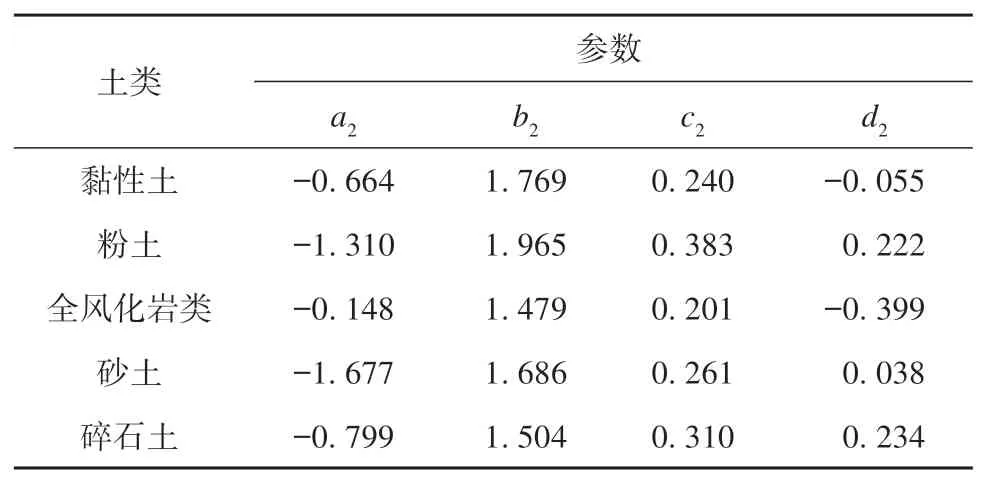
表4 热扩散系数三元拟合相关参数Table 4 Related parameters of ternary fitting for thermal diffusivity

3.1.3 径向基函数（RBF）神经网络

径向基函数（radical basis function）神经网络具有计算量小、学习收敛速度快及泛化能力强的特点，其较强的非线性函数逼近能力在诸多领域得以广泛应用［29-30］。将干密度、天然含水率及融土热扩散系数（冻土热扩散系数三元回归）作为RBF 神经网络的输入层，热扩散系数作为输出层，建立以高斯函数为隐含层激活函数的前馈型网络模型。同时，将走廊带内冻融土热扩散系数测试结果按9：1随机分块，其中90%样本数据用于神经网络模型的训练样本，剩余10%用作验证神经网络的预测能力。根据预测结果的反馈，对偏差较大的样本进行剔除，从而有效提高预测精度。图5 为全风化岩类融土热扩散系数的RBF 神经网络模型预测结果，可以看到预测值与实测值较为一致（R2=0.78，数据剔除比例为9%）。

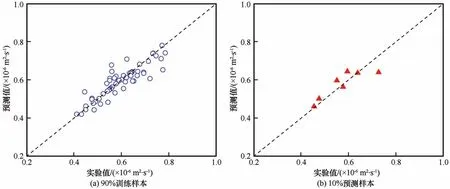
图5 全风化岩类融土热扩散系数RBF神经网络预测结果Fig.5 Prediction results of thermal diffusivity based on RBF neural network of unfrozen soil of fully weathered rocks

3.2 融土热扩散系数预测模型对比

图6为各土类融土热扩散系数两种预测模型的预测结果，可以看到两种预测模型所得预测值与实测结果整体较为吻合，大多数样本点分布在相对误差为10%范围内，证明了预测方法的有效性和工程应用价值。此外，对比两种方法预测值与实测值间差异分布，可发现RBF神经网络模型整体预测效果更佳。

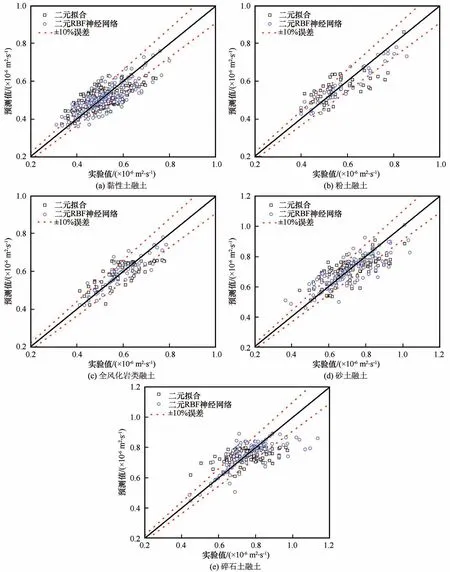
图6 各土类融土热扩散系数预测结果对比Fig.6 Comparison of prediction results of thermal diffusivity of unfrozen soil of different soil types

3.3 冻土热扩散系数预测模型对比

图7为各土类冻土热扩散系数四种预测模型的预测结果，同样可看到四种预测模型具有良好的预测性能。同时，对比四种方法预测值分布范围及与实测值间差异可发现，将融土热扩散系数纳入回归模型的三元预测方法较二元预测方法具有更宽的样本分布范围，且整体预测精度更高。

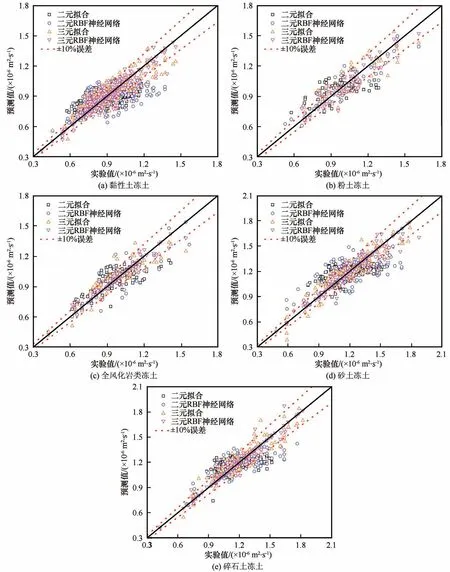
图7 各土类冻土热扩散系数预测结果对比Fig.7 Comparison of prediction results of thermal diffusivity of frozen soil of different soil types

3.4 走廊带内冻融土热扩散系数预测方法对比及应用总结

表5和表6 分别为冻融土热扩散系数预测模型所得结果的相关系数R2和相对误差在10%内占比，由表可知融土热扩散系数两种预测方法中RBF 神经网络在剔除样本比例少的情况下，各土类预测精度均显著高于二元拟合方法，其中粉土融土预测效果最好，相关系数R2和相对误差10%内占比分别为0.90 和82%。同时，对比冻土热扩散系数预测模型可发现，三元模型预测效果明显优于二元模型，进一步说明融土热扩散系数包含有重要的土壤成分信息，可有效弥补不完全参数回归模型的缺陷。此外，三元RBF 神经网络方法要优于三元拟合方法，说明RBF 神经网络方法可高效捕捉热扩散系数与影响因素间关系特征，进而有效提升预测精度，其中全风化岩类预测效果最好，相关系数R2和相对误差10%内占比分别为0.96和90.77%。

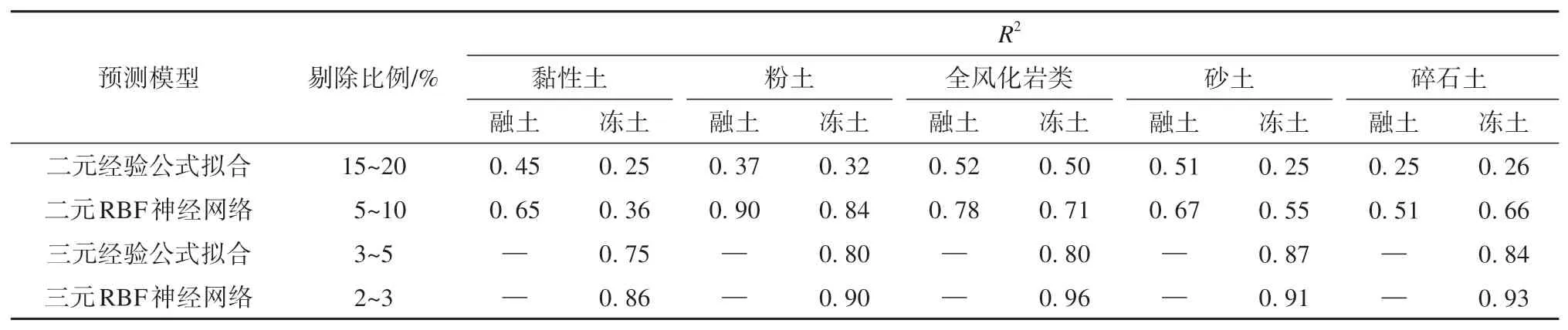
表5 热扩散系数预测模型相关系数R2Table 5 Correlation coefficient R2 of thermal diffusivity prediction models

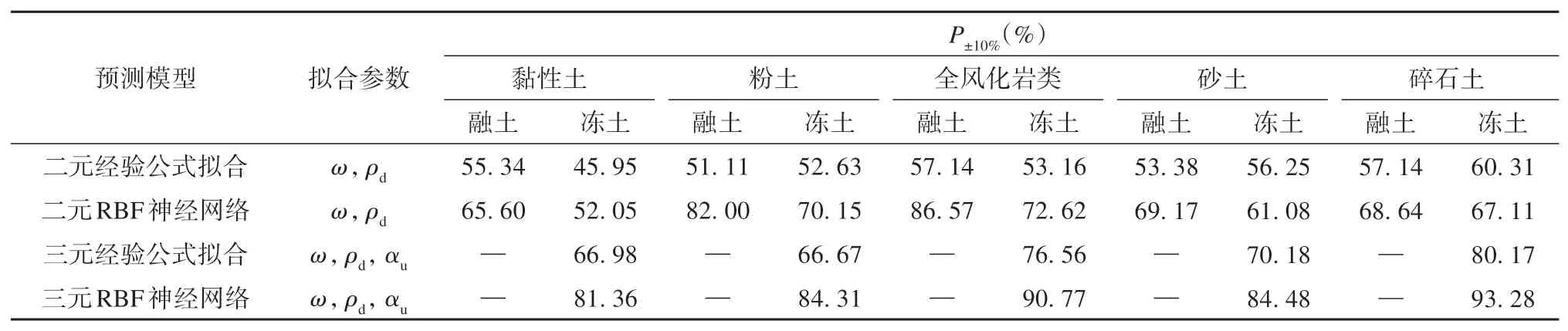
表6 热扩散系数预测模型相对误差在±10%内占比Table 6 The relative error of the thermal diffusivity prediction models is within±10%

依据前述分析可知，青藏工程走廊带各土类冻融土热扩散系数分布离散，不同预测方法应用总结如下：

（1）二元拟合方法针对于热扩散系数主体分布区间，其应用范围较窄且误差较大，但获取形式简单（只需干密度和含水率参数），可满足一般工程估算的相应要求；

（2）三元拟合方法局限于冻土热扩散系数，且不可避免高成本和冗长的实验测试过程，但具有适用样本分布范围广、预测性能好及应用简单的优点；

（3）RBF 神经网络需以大量实测样本数据和数学算法为基础，其开放性不强且应用相对复杂，但具有应用范围广、预测精度高的优势，总体来看该方法为热扩散系数最佳预测方法。

4 结论

本文针对青藏工程走廊典型土类的冻融土热扩散系数进行了计算，分析了热扩散系数分布特征和参数影响规律，提出了不同预测模型并对比了预测效果，得出主要结论如下：

（1）走廊带土类以黏性土、砂土和碎石土居多，热扩散系数与土类粒径整体呈正相关性，具体为融土热扩散系数按黏性土、粉土、全风化岩类、砂土及碎石土依次增大，冻土热扩散系数按黏性土、全风化岩类、粉土、碎石土及砂土依次增大。

（2）热扩散系数与干密度及天然含水率相关性随土类及冻融状态差异明显，冻、融土热扩散系数呈显著正线性关系。

（3）融土热扩散系数预测模型中，二元RBF 神经网络预测效果显著优于二元经验公式；冻土热扩散系数预测模型中，基于融土热扩散系数的三元预测模型的预测精度明显高于二元模型，且三元RBF神经网络模型预测效果更佳。

（4）综合热扩散系数不同预测模型预测效果和误差分析可得，二元拟合方法形式简单，可满足一般工程估算需求；三元拟合方法需以融土实验结果为基础，适用样本分布范围广且预测精度高；RBF神经网络模型具有最优的预测精度且应用范围最广，为最佳预测模型。