大跨钢箱梁斜拉桥施工期结构参数敏感性分析

张亚海， 朱斌， 郭宝圣， 南飞， 鲁乃唯

(1.中交路桥华东工程有限公司，上海市 201210；2.江西省交通运输科学研究院有限公司； 3.长沙理工大学 土木工程学院)

近年来，国内外建设了一批特大跨斜拉桥，如著名的荆岳长江大桥、苏通大桥等。随着斜拉桥主梁跨度的增加，钢箱梁结构逐步替代混凝土主梁，从而突显了钢箱梁斜拉桥在超大跨度桥型中的竞争优势。由于斜拉桥超静定次数较高，非线性显著，结构体系较为复杂，各构件设计参数合理匹配方能使得结构体系性能最优。通过结构参数的敏感性分析可掌握影响斜拉桥结构力学性能与安全性的主要参数，为结构优化设计与施工控制奠定基础。

国内外学者采用数值模拟与试验方法研究了钢箱梁斜拉桥的设计敏感参数。黄灿采用几何控制法对苏通大桥进行单因素敏感性分析，确定影响特大跨度斜拉桥施工控制误差的关键结构设计参数；刘榕等基于有限元法对不同结构类型的矮塔斜拉桥进行结构设计参数敏感性分析；邬晓光等研究了双钢拱塔斜拉桥施工期的结构参数对成桥状态的影响，表明拉索初张力和温度作用是影响钢主梁位移的主要因素；黄平明等开展了斜拉式桁架梁桥的参数敏感性分析，认为混凝土收缩徐变、温度、非线性等参数对结构的内力影响小，但对主梁挠度影响较大；刘世明等研究了无背曲塔曲梁斜拉桥施工期的敏感参数，认为整体降温和结构自重对索塔与主梁挠度以及拉索索力的影响较大；谢明志等研究了主跨926 m的鄂东长江大桥的几何控制参数敏感性，认为边跨索力受结构参数变化较为敏感，而中跨线形受结构参数较为敏感。常规有限元法和试验方法对结构参数变化组合难以确定，在多参数敏感性分析方面存在一定的局限性。

该文采用有限元数值模拟与无量纲参数敏感性分析方法，对某主跨为760 m的大跨度钢箱梁斜拉桥进行参数敏感性分析，确定斜拉索、主梁、索塔等构件的关键设计参数变化对全桥线形、内力等力学参数的影响程度，为大跨度钢箱梁斜拉桥结构参数的优化设计奠定理论基础。

1 结构参数敏感性分析方法

由于桥梁结构设计参数理论值与工程中实际结构参数取值总存在着一定的偏差，导致桥梁结构的实际受力状况与理想设计状况存在一定误差。利用有限元数值模拟方法构建与实际结构相适应的系统模型，对复杂桥梁结构进行结构设计参数敏感性分析至关重要。通过参数敏感性分析，确定各结构设计参数与结构响应之间的影响规律，为桥梁结构优化设计与过程误差控制提供科学依据。

针对某桥梁结构系统，假定其系统F主要由n个因素，a={a1,a2,a3,…,an}所确定，有：

F=f(a1,a2,a3,…,an)

(1)

(2)

式中：φk(ak)为系统特性F对ak的敏感性。

为了能够对多参数系统特性中不同量纲的各参数的敏感程度进行对比分析，对参数进行无量纲处理。因此，定义了无量纲化参数敏感性函数与敏感因子，参数ak的敏感度函数Sk(ak)为：

(3)

式中：k=1,2,3,…,n；δF为系统特性F的相对误差；δak为参数ak的相对误差。

当δak较小时，Sk(ak)可表示为：

(4)

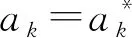
中水系统投用后近两年的化验分析数据表明，各工段处理正常，如图4所示，COD（蓝实线）及氨氮（红虚线）处理效果得到改善。

(5)

2 某钢箱梁斜拉桥施工阶段仿真分析

2.1 工程概况

某大跨度斜拉桥为全长1 610 m的双塔双索面半漂浮体系钢箱梁斜拉桥，跨径布置为(100+275+760+275+100) m，立面布置如图1所示。主梁结构形式为PK断面钢箱梁，箱梁高4.0 m，全宽46 m。索塔结构为钻石形，索塔高233.7 m，整体式承台配大直径

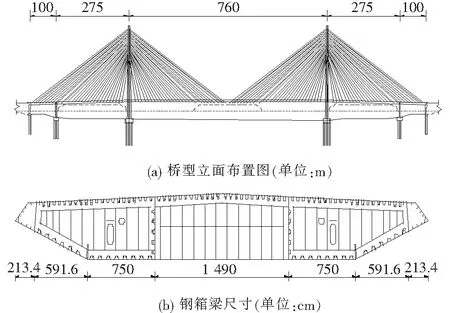
图1 某斜拉桥结构设计图

群桩基础。斜拉索采用极限强度1 860 MPa平行钢丝斜拉索对称布置，全桥共4×30×2=240根斜拉索。

2.2 有限元模型

采用有限元程序Midas/Civil 建立全桥有限元分析模型，如图2所示。全桥共离散为2 105个节点，1 778个单元，其中包括1 538个梁单元，240个索单元(斜拉索)。使用空间梁单元模拟主梁、桥塔，桁架单元模拟斜拉索。主梁的边界条件均采用弹性连接模拟，主梁与边墩之间施加竖向及横桥向的弹性连接，主梁与辅助墩间施加竖向弹性连接，桥塔处主梁通过弹性连接约束，在桥塔下横梁上和塔柱上分别进行竖向、横向约束。

图2 有限元计算模型

有限元模型中，考虑拉索弹性模量、主梁刚度、主梁重度、桥塔刚度等4个主要结构物理参数对大跨度钢箱梁斜拉桥的影响，分别取基准状态下各自取值的85%、90%、95%、100%、105%、110%、115%，各结构设计参数具体取值如表1所示。

表1 结构参数取值

2.3 施工阶段模拟

根据施工方案，该斜拉桥的上部结构钢箱梁除索塔附近外，均采用悬臂吊装架设方案，半跨节段29榀梁段。具体施工流程如图3所示。

相对同类型桥梁的施工工艺，该桥梁施工具有以下特征：① 悬臂端较长，刚度较低，温度等荷载对施工期的主梁线形影响较大；② 两个索塔及各自悬臂的临时荷载具有不对称特征；③ 非线性效应显著。针对上述施工阶段特征，将有限元分析模型共划分为36个施工阶段。由于中跨合龙精度控制至关重要，该文选取中跨合龙前的悬臂施工阶段，分析结构参数对其内力与位移的影响。

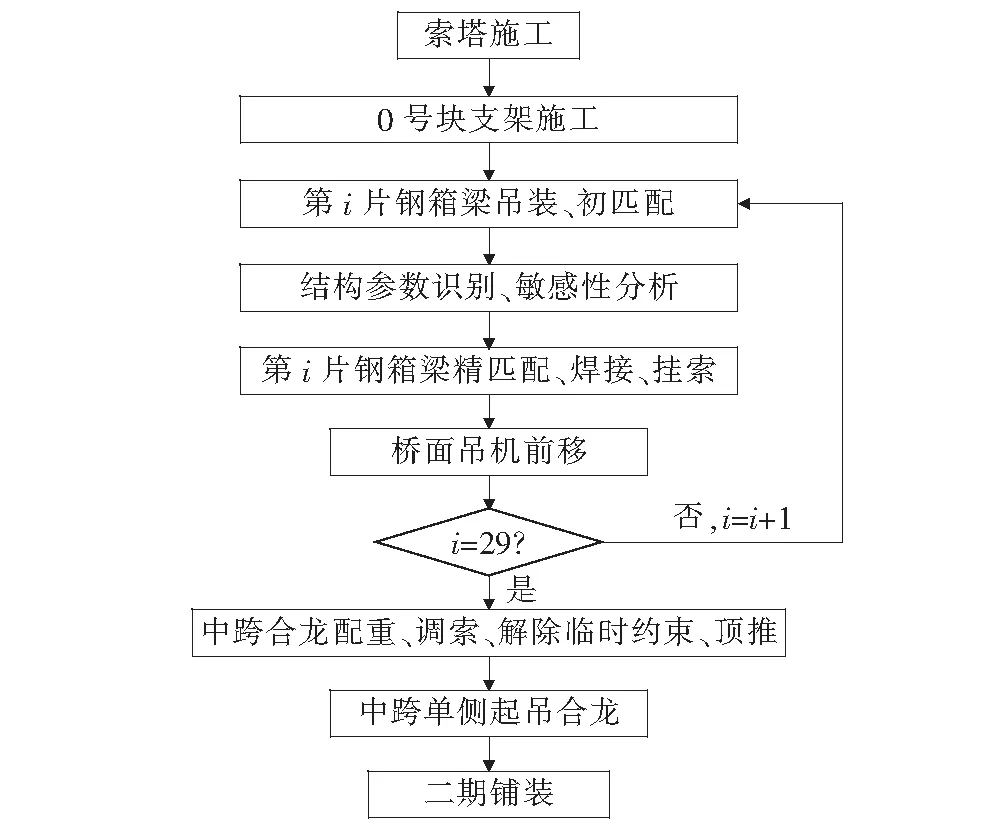
图3 某斜拉桥施工步骤

3 斜拉桥悬臂施工阶段敏感性参数分析

3.1 主梁变形参数分析

主梁线形是大跨度斜拉桥在施工阶段与成桥运营期需控制的重要参数之一。因此，通过大跨度斜拉桥悬臂施工阶段的参数敏感性分析，明确不同结构设计参数对主梁位移的影响规律，是主梁线形控制、参数识别的重要依据。该文应用无量纲参数敏感性分析方法，分别对主梁的中跨、边跨这两个关键控制位置竖向位移进行结构参数敏感性分析。由于篇幅较大，下面仅给出拉索弹性模量对中跨悬臂端部位移影响的分析过程。选取拉索弹性模量ES基准状态下取值的85%、90%、95%、100%、105%、110%、115%进行变化，计算出主梁中跨悬臂端部竖向位移μ，并绘出μ-E曲线图，如图4所示。

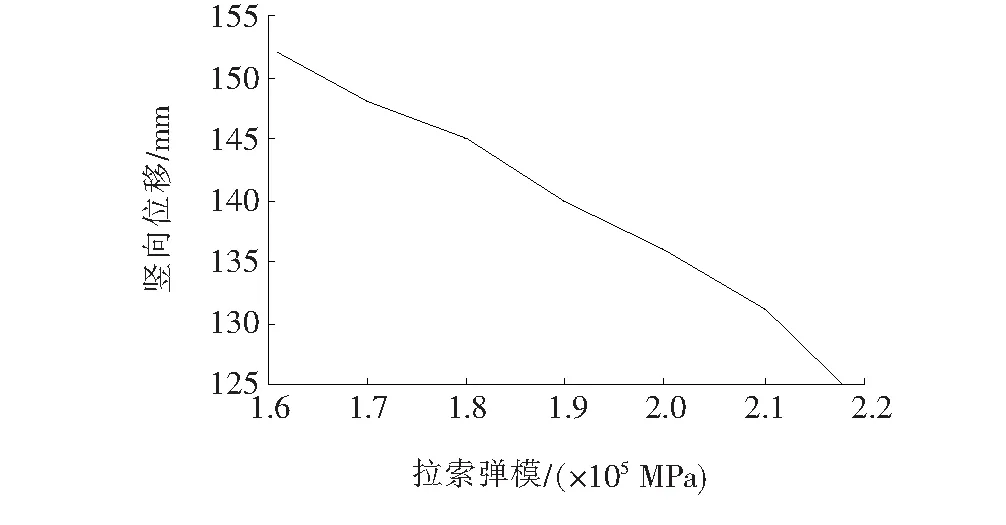
图4 拉索弹模与主梁跨中位移关系曲线

由图4可知：主梁中跨悬臂端竖向位移随拉索弹性模量的增加而逐渐减小，且呈非线性变化趋势。依次选取主梁刚度SG，主梁重度γG和索塔刚度ST，各结构设计参数基准值对主梁中跨、边跨悬臂端部的竖向位移的敏感性分析分别如图5、6所示。

图5 主梁中跨悬臂端位移的参数敏感性

图6 主梁边跨悬臂端位移的敏感性分析图

由图5可知：主梁中跨悬臂端的竖向位移受斜拉索弹性模量的影响最为敏感，其敏感度因子为0.613。换言之，若斜拉索弹性模量取值变化5%，则引起主梁中跨悬臂端竖向位移变化的相对误差为3.065%。索塔刚度是最不敏感参数，若其误差为5%，引起则主梁中跨悬臂端竖向位移的相对误差仅为0.175%。通过敏感性百分比分析可知，斜拉索弹性模量和主梁重度对主梁中跨悬臂端竖向位移影响的敏感性占比分别为47%和44%，是影响主梁中跨悬臂端竖向位移的主要参数；主梁刚度对主梁中跨悬臂端竖向位移影响的敏感性占比为6%，为次要影响参数；索塔刚度的敏感性占比小于3%，对主梁中跨悬臂端竖向位移影响很小，为可忽略影响参数。

由图6可知：主梁重度对主梁边跨悬臂端的竖向位移的影响最为敏感，敏感度因子为-0.217，换言之，主梁边跨悬臂端竖向位移随主梁重度每增加5%而将增大约1.085%；拉索弹性模量变化对主梁边跨竖向位移的影响次之，敏感度因子为0.135；主梁刚度、索塔刚度的敏感度因子较小，分别为0.048、0.029。从敏感性百分比分析可知，主梁重度对主梁边跨悬臂端竖向位移的敏感性占比为51%，是重要影响参数；拉索弹性模量的敏感性占比为31%，是影响主梁边跨悬臂端竖向位移的主要参数；主梁刚度和索塔刚度的敏感性占比分别为11%、7%，是主梁边跨悬臂端竖向位移的次要影响参数。

针对该桥而言，悬臂施工阶段的荷载较为均匀，索塔的横向偏位数值较小，导致边、中跨主梁位移对索塔的刚度并不敏感。刘吴苏等对矮塔斜拉桥的敏感分析结果与该文分析结果相似，即索塔刚度的变化对主梁位移影响较小，但对索塔的横向偏位有较大影响。然而，由于特大跨斜拉桥悬臂施工阶段的不均匀荷载等因素，往往导致索塔产生一定的横向偏位，此时索塔刚度会对主梁悬臂端位移影响较大。因此，该文的结论仅适用于悬臂荷载相对较均匀的理想情况，在施工过程中有较大的索塔偏位时需慎重分析。

对于大跨度斜拉桥，若以主梁竖向位移为控制指标，对拉索弹性模量与主梁重度的计算值选取应慎重。考虑各结构设计参数对索塔塔顶顺桥向位移的影响进行敏感性分析，各参数基准值的敏感性分析如图7所示。

从图7可知：索塔塔顶纵向位移受索塔刚度变化的影响最为敏感，敏感度因子为0.768；主梁重度对桥塔偏位的影响次之，敏感度因子为-0.453，而其他两个设计参数敏感度因子均很小。从敏感性百分比来看，索塔刚度对索塔纵向偏位的敏感性占比为61%，是影响索塔偏位的重要参数，主梁重度对索塔偏位的敏感性占比为36%，是影响索塔偏位的主要参数，其余两个结构参数敏感性占比之和小于3%，对索塔偏位的影响可忽略。

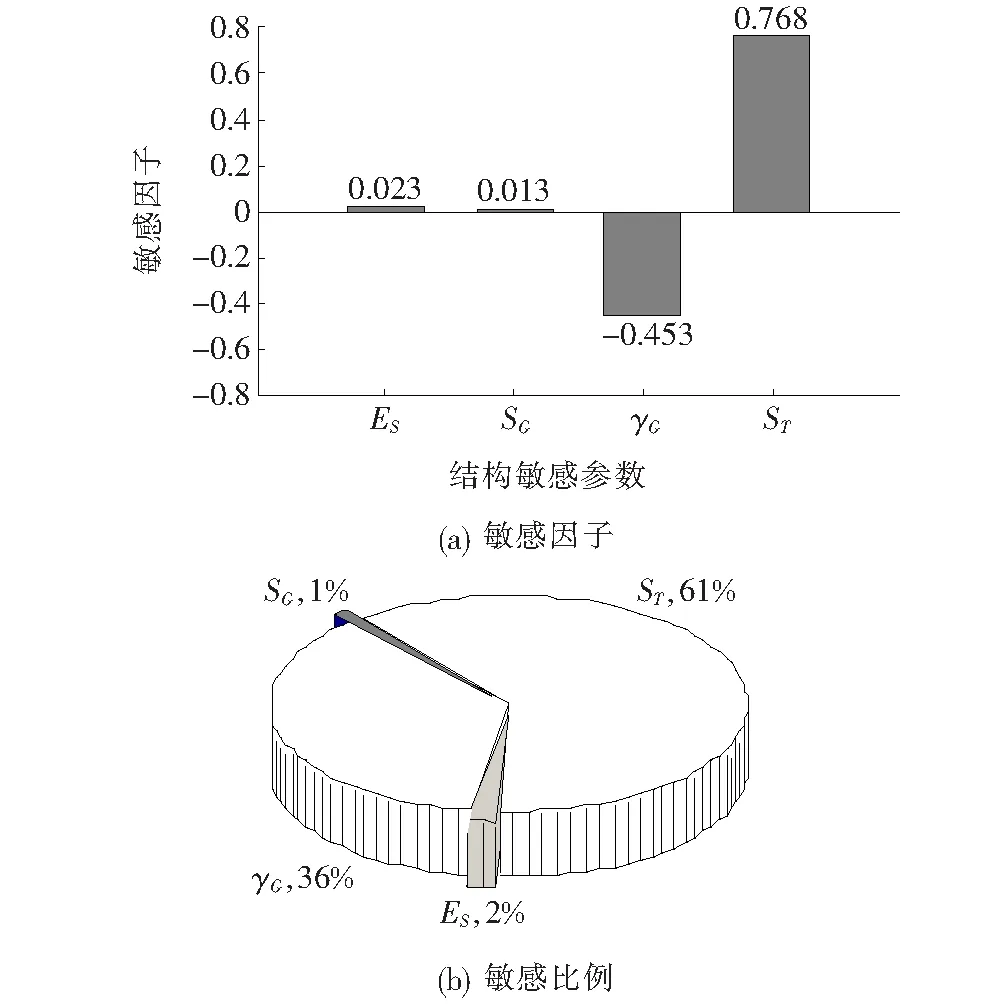
图7 索塔偏位的敏感性分析图

3.2 索力敏感参数分析

大跨度钢箱梁斜拉桥的斜拉索索力是施工过程控制和实现合理成桥状态的重要参数之一，该文分别对中跨合龙前的最长斜拉索和最短斜拉索的索力进行无量纲参数敏感性分析，各参数基准值的敏感因子如图8、9所示。

图8 长索索力的敏感性

由图8、9可知：斜拉索索力受拉索弹性模量影响最为敏感，拉索弹性模量对最长拉索索力和最短拉索索力的敏感因子分别为0.545、0.677；主梁重度对斜拉索索力的敏感程度次之，主梁重度对最长拉索的影响较最短拉索的影响更为明显，对最长拉索的敏感因子为0.208，对最短拉索的敏感因子为0.071。从敏感性百分比分析可知，拉索弹性模量对最长拉索索力和最短拉索索力的敏感性占比分别为69%、86%，为重要影响参数；主梁容重对最长拉索索力影响较最短拉索索力大，为次要影响参数；主梁、索塔的刚度对斜拉索索力的敏感性占比最大只有3%，可忽略不计。

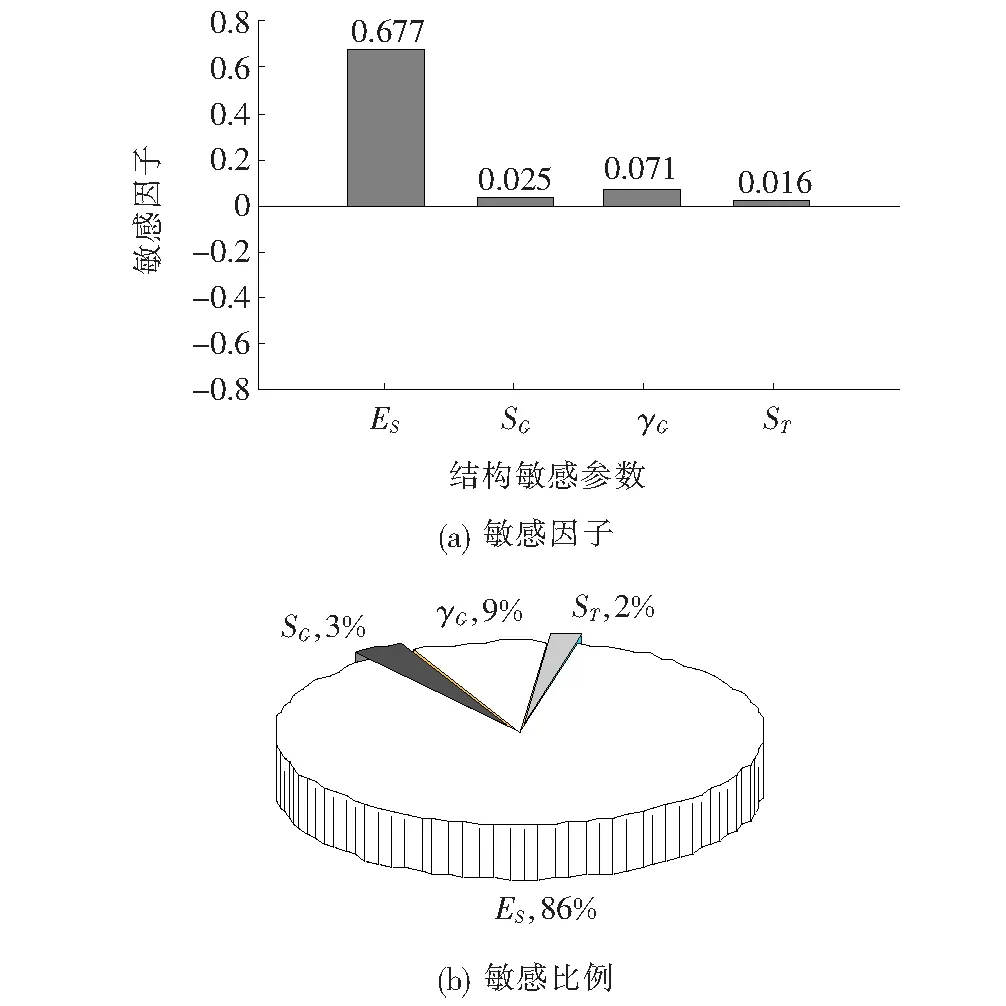
图9 短索索力的敏感性

3.3 主梁弯矩敏感参数分析

考虑各结构设计参数对主梁最大弯矩的影响进行敏感性参数分析，各结构参数基准值的敏感因子如图10所示。

由图10可知：主梁弯矩受主梁重度的影响最为敏感，受拉索弹性模量的影响次之，敏感度因子分别为-0.593、0.578。索塔刚度的敏感度因子仅为0.023，主梁刚度的敏感度因子接近于0，因此，索塔和主梁的刚度对主梁弯矩的影响程度可忽略。从敏感性百分比可知，拉索弹性模量、主梁重度对主梁最大弯矩的敏感性占比分别为48%和49%，是主要影响参数，而主梁和索塔的刚度对主梁最大弯矩的敏感性占比之和小于3%，是可忽略的影响参数。

4 结论

以某大跨度钢箱梁斜拉桥为研究对象，采用结构该文未考虑多个结构参数对大跨度钢箱梁斜拉桥复合作用下的结构响应的影响，若要考虑可采用响应面、神经网络、学习机器等先进的函数拟合方法进一步研究多参数的敏感效应。此外，有待开展考虑结构参数的随机敏感性参数分析。

图10 主梁最大弯矩的敏感性

系统特性的无量纲敏感参数分析方法，开展了钢箱梁中跨悬臂施工阶段的结构设计参数敏感性分析，识别了斜拉索弹模、主梁刚度、索塔刚度等参数对桥梁线形与内力的影响规律，得出以下主要结论：

(1) 拉索弹性模量对索塔与主梁中跨悬臂端的位移较为敏感，主梁重度对主梁边跨位移较为敏感，而主梁与索塔刚度对主梁悬臂端挠度影响相对较小。

(2) 斜拉索索力主要受拉索弹性模量的影响较大，拉索弹性模量对短斜拉索索力的影响大于长索，主梁重度对长斜拉索索力影响较最短索大。

(3) 拉索弹性模量、主梁重度对主梁内力影响较敏感，而索塔与主梁的刚度是可忽略影响参数。