基于概率跳跃粒子群算法的钢桁拱桥结构线形优化

康俊涛， 刘开， 张亚州

(武汉理工大学 土木工程与建筑学院， 湖北 武汉 430070)

钢桁拱桥拱肋的线形是拱桥概念设计的重要参数，它直接影响了整个桥梁的受力性能、应力分布、整桥重量。目前确定拱轴线形的方法多是通过荷载产生的压力线来确定，即设计线形，使得拱上只承受压力，不承受弯矩，由于实际结构承受的荷载复杂，理想的拱轴线是无法得到的，因此，现在常用的方法多为“五点重合法”，即拱肋上几个关键点的压力线与拱轴线相重合。首先只采用5个关键点对结构线形控制不能保证选择的线形为最优方案，即使增加关键点数，采用“多点重合法”，也无法解决有限点数带来的误差，且增加了计算的复杂度，使得问题更加难以采用理论解法给出最优方案；其次，现有拱肋线形的确定具有一定的经验成分，如抛物线次数、圆曲线半径等控制因素多为离散经验值，无法对所有解空间进行全部的探索，从而导致可能遗漏最优方案现象的发生。

近年来，越来越多的学者将智能优化算法应用于土木工程领域，如结构优化(索力值、拱轴线形等)、结构损伤识别等。相比于传统算法，智能算法具有计算速度快，且对经验知识要求少的特点。李剑桥采用粒子群算法对大跨径上承式钢管混凝土拱桥拱轴线进行了优化，在结构安全性、经济性方面均取得了良好的成果；王超采用粒子群算法解决了桥墩设计中的抗震问题，很大程度上提高了优化后桥梁的抗震能力；崔凤坤将BP神经网络和粒子群算法相结合，然后应用于拱桥的安全度分析中，提高了安全度计算的精度。由此可见，将智能算法合适地应用于土木工程领域可以获得良好的结果，然而目前在土木工程中应用的智能算法多为标准算法，即未对算法本身进行过多干预和改进，而智能算法具有一个弊病——易于陷入局部最优，导致无法找到最优解决方案。因此，该文通过对标准粒子群算法的进化公式进行分析，提出粒子跳出局部最优的解决方案，然后将其应用于钢桁拱桥的拱肋线形优化上，同时采用标准粒子群算法作为对比，以验证所提算法的寻优精度和效率。

1 优化模型

1.1 优化变量

在某钢桁架拱桥结构中，拱肋结构几何对称，取半拱结构分析，如图1所示。

下弦杆为二次抛物线形式，拱肋上弦杆为两段圆曲线与一段二次抛物线组合的形式。在确定桥梁跨径布置以及桥梁起点的情况下，图中的坐标参数x1、y1、y2、x3、y3、x4为已知参数，利用曲线之间相切的关系，可以得出y0与其他未知参数之间的关系，因此为确定拱肋线形，需要拟定一下参数：① 拱脚高度H1；② 拱顶高度H2；③ 边跨圆曲线半径R1；④ 中跨圆曲线半径R2；⑤ 中跨圆曲线和二次抛物线交点顺桥向坐标x0；⑥ 拱肋下弦杆跨中顶点竖向坐标y4，利用以上参数可以确定出拱肋各曲线方程为：

拱肋下弦杆：

(1)

上弦杆抛物线：

(2)

由于上弦杆两个圆曲线上面均知道两个已知点和半径，所以圆方程为确定方程。拱顶拱脚高度主要取决于成桥运营阶段产生的内力，这些参数数值取得过高或者过低，会使钢桁架拱肋腹杆长度加大，不利于压杆稳定，同时会加大桥梁的建设成本，对桥梁的安全运营产生不利影响；边中跨圆曲线半径以及交点坐标取决于桥梁跨径布置，会对桥梁整体受力以及美观性产生较大影响。综合考虑，给出各参数的取值范围如表1所示。

1.2 目标函数

钢桁架拱桥的拱肋线形优化就是在给定范围的各个参数中，选出最合适的一组参数，使得优化的目标函数值达到最理想取值。对钢桁架拱桥拱肋结构线形优化，由于拱肋杆件主要承受压力以及弯矩，因此选取全桥梁单元的弯曲应变能和拉压应变能作为该桥的优化目标，目标函数表达式如下：

U=

(3)

由于结构为离散单元，且全桥用钢的弹性模量相同，因此式(3)可简化为:

(4)

式中：MLi、MRi、NLi、NRi分别为第i个单元左右端弯矩和轴力；li、Ii、Ai分别为第i个单元的长度、惯性矩和截面积。为了便于计算同时消除量纲的影响，该文将初始设计的桥梁弯曲应变能和拉压应变能作为基准1，这样优化效果也更加直观。

2 概率跳跃因子粒子群算法

2.1 标准粒子群

粒子群算法属于生物启发算法，通过模拟群体生物的捕食过程来完成最优解的寻找过程。在粒子群算法中，每一个粒子被模拟为可行域内的解，粒子的位置为解的参数值，粒子的适应度值为解的优劣评价标准。在每轮迭代中，粒子的飞行方向可用式(5)、(6)表示：

(5)

(6)

2.2 概率跳跃因子粒子群算法

2.2.1 算法思想

由于标准粒子群算法的速度惯性权重，全局最优权重学习率和个体最优权重学习率均为定值，因此粒子的活动途径受到了一定的限制，特别是当粒子活动后期，粒子个体最优和实际位置之间的差值很小，从而导致粒子的活动范围受到限制，因此标准粒子群具有易于陷入局部最优的缺点。一些学者通过调整粒子的速度惯性来平衡算法的全局和局部寻优能力，但是多为确定性的权重，在迭代前期具有良好的效果，但在粒子聚集后仍不具有跳出局部最优的能力。

通过对粒子行进方式进行调整，一些学者提出了量子粒子群，粒子的行进方向由波动方程确定，使得粒子具有了概率性质，提高了粒子跳出局部最优的能力。相比量子粒子群，标准粒子群的速度更新方式更为简单，且更加直观，方便学者根据问题特点进行改进。因此该文拟将量子思想加入到标准粒子算法中，在保持粒子更新方式简单的基础上，提高粒子全局搜索能力，以此基础和目的提出了跳跃因子。

2.2.2 概率跳跃因子

为防止粒子在局部最优处过于聚集，该文提出对粒子的聚集度和进化速度进行监控，并根据监控结果对部分粒子进行调整。

(1) 聚集度

当粒子在一个区域过于聚集，会造成多数粒子的寻优贡献减小，降低优化效率。通过监控粒子的聚集程度来对粒子行为进行动态调整，这样无需预先设定权重变化公式和路径，对粒子进化具有更强的适应性，因此该文定义粒子的聚集度为：

(7)

式中：N为粒子的总数；pbi为第i个粒子的个体最优位置；gb为种群的全局最优位置。当Sd>α时(α为设定的一个值，可根据问题进行调整，该文设置为1×10-3)，认为粒子的聚集度过大，在全局最优附近增加更多的粒子并不会改善算法的寻优精度，且由于多数粒子的寻优途径相近，会造成计算效率低下。

(2) 粒子进化速度

在标准粒子群迭代后期，粒子往往会聚集冗余，为了解决此问题，学者通过设置粒子在进化速度慢时对粒子惯性进行操作，如果设置当粒子迭代一个固定次数时调整速度惯性权重，由于粒子的迭代速度是未知的，因此可能会在一定次数后仍有很高的进化速度，导致效果不佳。该文根据全局最优解的变化速度来设定粒子的变化时间：

(8)

式中：Svt为第t次迭代种群的进化速度；obj(gbt)为全局最优对应的目标函数值；Tb为判断距离，Tb越大则对全局最优变化越不敏感，算法的迭代曲线越平顺，反之，则算法对全局最优的进化速度越敏感，粒子也更易发生震荡现象。

(3) 概率跳跃

当满足条件Sd>α且Sv>β时，认为粒子的进化慢，且有冗余，粒子的进化方式应进行改变。该文提出随机概率跳跃因子来改变部分粒子的位置：

(9)

当满足条件时，从种群中随机选择一个粒子，并将其位置进化方式改为随机进化，粒子的位置服从N(p,σ)的整体分布，其中均值p为该粒子历代个体最优中随机选择的一个值，方差σ可以根据问题特点进行设定，该文取方差为1×10-3。

2.2.3 算法流程

带有概率跳跃的粒子群算法的步骤如下。

步骤1：在定义域内随机初始化种群。

步骤2：将粒子的位置初始化为粒子的个体最优，全局最优根据个体最优进行初始化。

步骤3：根据式(5)、(6)计算粒子下一轮迭代的速度和位置，然后更新粒子。

步骤4：根据式(7)、(8)判断是否进行跳跃，如果是则根据式(9)选择粒子进行跳跃，否则进行下一步。

步骤5：更新个体最优和全局最优。

步骤6：判断是否满足迭代终止条件，是，则结束迭代输出结果，否则进入步骤3。

具体算法流程见图2。

图2 RPSO算法流程图

2.3 算法对比

采用多峰值函数Rastrigin函数进行测试，函数方程如式(10)所示，图像如图3所示。算法迭代过程见图4。

(10)

式中：xi范围为[-1.5,1.5]，式中参数取值为：n=2，函数在定义域内有9个极小值，对称分布于xi值为±0.5、±1.0处，其中[0,0]处为全局最优解，目标函数值为0。

从图4中可以看出：增加概率跳跃之后，算法的寻优精度有明显改善，而标准粒子群寻找到的全局最优位置为[-1.0,0]+[-1.235×10-12,2.162×10-13]，表明算法寻找到了局部最优解，而非全局最优解[0,0]。带有概率跳跃算法的粒子群寻找到的全局最优位置为[5.526×10-17,3.335×10-20]，为定义域内的全局最优所处位置。从粒子的迭代过程可以看出基础明显的跳跃位置，说明了算法设置的合理性。

图3 Rastrigin函数三维图

图4 算法迭代过程图

3 工程案例

3.1 工程概况

研究对象为某中承式钢桁架拱桥，桥跨布置为(70+240+70) m，初始设计为拱肋跨中矢高56.314 m，拱轴线矢跨比1/4.261，拱肋跨中高度7 m，拱脚高度20.559 m，拱肋下弦杆为二次抛物线，拱肋上弦杆中，边跨部分为圆曲线，半径为300 m，中跨部分为圆曲线与二次抛物线组合形式，圆曲线半径为280 m，全桥总用钢量为14 863.3 t。为确定拱肋线形的最优形式，该文采用RPSO法进行优化，并且采用Kriging代理模型来减少优化时间，提高优化效率。

3.2 Kriging代理模型

智能算法在每轮迭代中均需要计算每个新粒子的适应度，且智能算法为了保证精度，往往会设置较大数目的个体，因此智能算法具有计算量大的特点。为了加速迭代，一些学者采用了代理模型的解决方案，即采用一个简单的、显式的关系来替换设计参数与目标量之间的隐式有限元关系。由于显式的计算消耗较有限元模型的计算消耗明显减小，因此采用代理模型后可以极大地提高优化效率。

常用的代理模型有响应面模型、神经网络模型(ANN，RBF)、Kriging模型等，响应面模型和神经网络模型属于确定性模型，即当样本点确定之后，每个样本点对所有预测点的贡献是相同的，而Kriging属于半确定半概率模型，即每个样本点对预测点的贡献是不同的。

Kriging模型由确定性的多项式部分和概率性的随机部分组成，如下式所示：

(11)

式中：fT(x)β为线性回归部分，β为线性回归系数。线性回归函数fT(x)可以选用零次(常数)、一次、二次等形式，次数越高，线形部分对数据的拟合越好，但过高的次数容易出现过拟合的现象，因此一般选择二次为优；z(x)为随机误差部分，随机误差是一个期望为0的高斯平稳随机分布。它服从正态分布N(0,σ2)，并具有以下性质：

(12)

式中：R(θ,ω,x)为相关函数，是关于预测点与样本点之间距离的函数，距离越大，样本点对预测点的影响越小。

3.3 优化过程及结果分析

利用拉丁超立方法进行抽样，将抽取的样本点代入钢桁拱的线形方程，确定拱上每点的坐标，然后建立有限元模型，计算结构的响应。

在设计变量的可行域内共抽取了200个样本点，然后根据样本点与对应响应之间的关系建立Kriging代理模型(表2)，同时观察MSE(均方误差)，检验代理模型的拟合精度。

表2 Kriging代理模型信息

从表2中可以看出：Kriging模型的MSE非常小，表明代理模型精度较高，可以用于后续的寻优过程。

采用概率跳跃粒子群算法进行寻优，同时采用标准粒子群算法进行对比，观察算法改进前后的寻优精度和寻优效率。算法设置如表3所示。优化结果如表4所示。

表3 算法参数设置信息

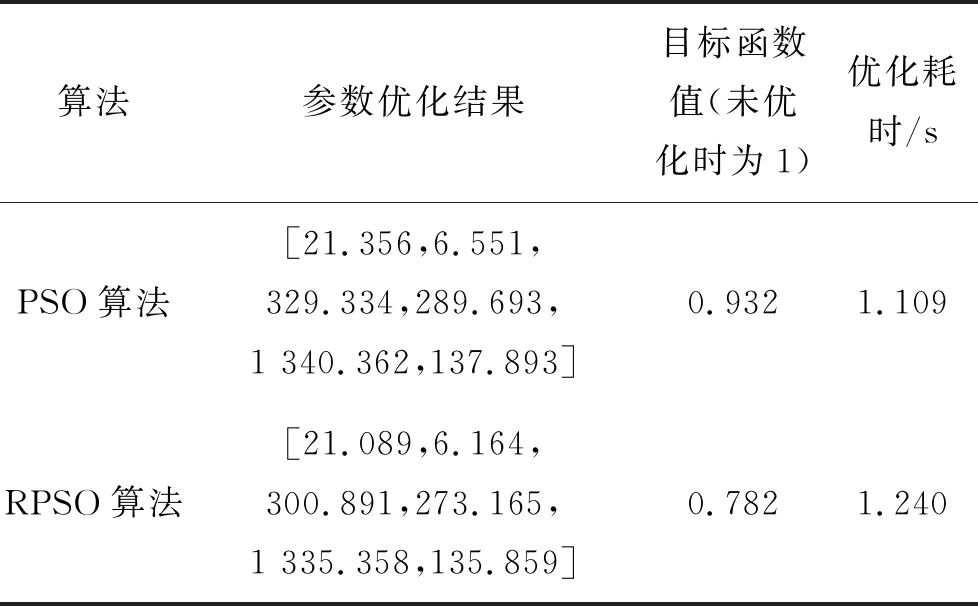
表4 两种算法优化结果对比

从表4可以看出:RPSO的优化结果明显优于标准PSO，并且两种算法优化的参数结果也位于不同位置。由于优化参数为6维，且优化变量与结构输出之间的关系复杂，因此问题存在多个局部峰值，增加了寻找全局最优解的困难。在寻优时间上，由于该文设置的终止条件未达到最高迭代次数，因此两种算法相差不大，表明增加随机跳跃后，算法的复杂程度并未增加很多。表5为3种情况下主拱肋的应力位移计算结果。图5为PSO及RPSO两种算法目标函数值的对比结果。

由表5可知：RPSO优化后，主拱肋压应力比设计减小了13.88 MPa，拉应力减小了9.44 MPa，竖向位移减小了13.73 mm，应力和位移减小幅度均比PSO优化要大，优化效果更加明显。

表5 3种情况主拱肋应力位移计算结果

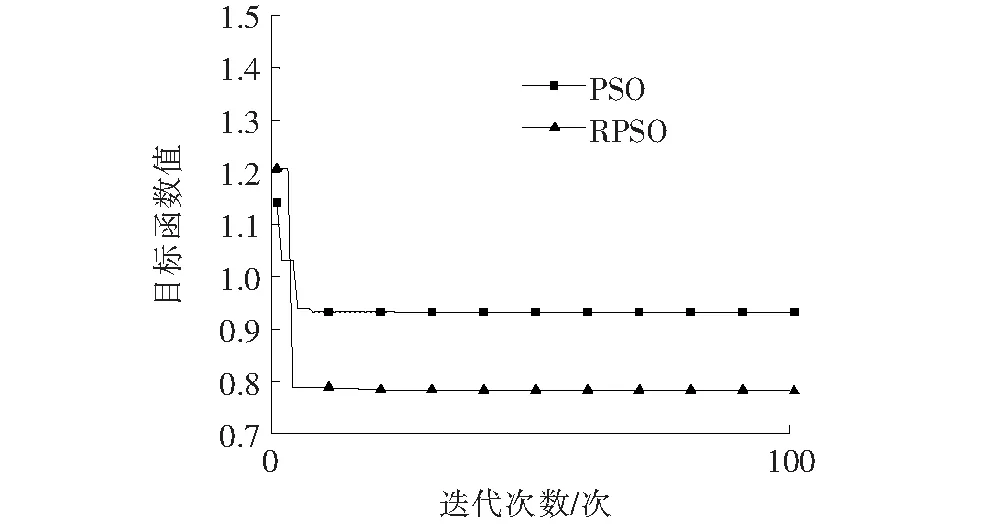
图5 目标函数迭代对比图

从图5可以看出：优化后结构的线形满足平顺要求。从算法的迭代过程图中可以看出，改进后的粒子群算法进化速度更快，且寻找到的解的精度也越高，即给出的拱肋线形方案更优。

4 结论

(1) 采用聚集度和优化速度作为粒子跳动时机的判别标准，可以有效防止粒子冗余，提高优化速度，且在相同迭代次数时，所提算法寻优精度更高。

(2) 经过对拱轴线上下弦杆线形的优化，桥梁主拱肋压应力减小了13.88 MPa，拉应力减小了9.44 MPa，竖向位移减小了13.73 mm，整体应变能减小了21.8%，全桥受力更加合理，同时可以为下一步节约钢材提供依据。