钢筋混凝土梁基于材料强度疲劳耗散的承载力退化模型
刘芳平,易文韬,闫磊
(1.河西学院 土木工程学院,甘肃 张掖 734000; 2.重庆三峡学院 土木工程学院)
钢筋混凝土梁在运营期间主要承受循环的汽车荷载作用,构成桥梁结构的钢筋与混凝土可能会在小于材料屈服(极限)强度的情况下产生疲劳破坏,有时尽管没破坏,但终会因材料强度疲劳耗散使结构极限承载力下降,造成一定的安全隐患。因此,材料强度疲劳耗散下的结构承载力研究具有非常重要的意义。在对类似于混凝土的复合材料剩余强度研究中,国内外许多学者都提出了不同的模型或表达式,但提出的这些剩余强度模型或表达式形式复杂、参数较多、试验验证较少、能确定模型参数的试验有效数据非常有限,导致剩余强度模型实际应用起来难度较大。对这些剩余强度的不同模型或表达式分析发现都符合其边界条件。在对受到疲劳荷载作用的钢筋混凝土结构中钢筋的剩余强度研究中普遍采用的是钢筋疲劳失效的“一元判据”,并得到了指数形式、对数形式、线性形式的退化模型,基于一元判据得到的这些退化模型描述钢筋疲劳破坏时是不足够精确的。以往主要依靠试验与数值模拟研究疲劳荷载作用下钢筋混凝土梁的剩余承载力。但试验研究需制作大批量试件,耗费大量人力、物力、财力,且易受试验本身条件的限制,得到数据也极其有限。已有的数值模拟方法理论复杂、无法有效模拟疲劳荷载作用下钢筋与混凝土的耗散。
该文从钢筋与混凝土强度退化过程出发,建立两种材料经历任意次数疲劳荷载作用后的剩余强度包络线方程,用其求解任意加载次数后的材料剩余强度;将静载作用下钢筋混凝土梁抗弯承载力计算理论和疲劳荷载作用下钢筋混凝土梁抗弯承载力计算假定融合,最终建立钢筋混凝土梁基于材料强度疲劳耗散的承载力退化计算模型,并通过算例进行验证,实现疲劳荷载作用下结构承载力退化规律的计算分析。
1 混凝土疲劳剩余强度计算
现有混凝土材料剩余强度计算式各有不同,但都基本满足如下边界条件:
(1) 剩余强度初值为未受载时的强度,也就是σr(0)=σ0,其中:未受载强度σ0取强度极限σb。
(2) 混凝土材料破坏时的剩余强度等于疲劳加载上限值,即σr(Nf)=σmax。
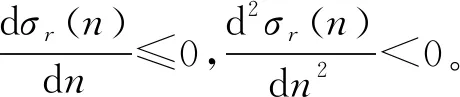
基于以上分析,该文从混凝土强度退化过程分析入手,通过研究材料疲劳剩余强度包络线方程求解任意次数加载作用后混凝土的强度。
1.1 确定包络线曲线形状
文献[9]、[10]研究表明:混凝土疲劳破坏时的最大应变与单轴静载下的最大应变相当,文献[11]验证了以上研究成果。仔细分析发现:混凝土在单轴静载下的应力-应变曲线软化段与疲劳荷载作用下的应力-应变滞回曲线十分接近,因此该文采用前者近似代表混凝土在疲劳荷载作用破坏时的剩余强度包络线(图1),并将其最大应力对应的应变作为疲劳破坏依据。
1.2 疲劳剩余强度包络线方程
GB 50010-2010《混凝土结构设计规范》中混凝土在单轴静载下的应力-应变曲线软化段方程如式(1)、(2)所示:
(1)
(2)
式中:ε>εc,ε>εt;αc为单轴受压应力-应变曲线软化段形状系数;αt为单轴受拉应力-应变曲线软化段形状系数;fc、ft分别为混凝土单轴抗压、抗拉强度;εc、εt分别为fc、ft对应的峰值压、拉应变。
参照单轴静载应力-应变曲线软化段方程(1)~(2)的求解方法和疲劳剩余强度包络线(图1),得到混凝土疲劳剩余强度包络线方程如式(3)、(4)所示:
(3)

(4)
式中:σr,c(N)为混凝土受压疲劳破坏时的剩余强度,σr,t(N)为混凝土受拉疲劳破坏时的剩余强度;x(N) 为与疲劳加载次数N有关的函数。
1.3 疲劳剩余强度求解
求解疲劳剩余强度包络线方程(3)、(4),得到任意次数加载后混凝土剩余强度为:
(5)
分析函数x(N)发现其符合以下两个边界条件:
(1)x|N=1=x(1)=1,σr,c(1)=fc;即第一次加载时的应力为混凝土材料的轴心抗压强度。
(2)x|N=Nf=x(Nf),σr,c(Nf)=σmax;即疲劳破坏时混凝土材料的抗压剩余强度退化为疲劳上限应力。
因此,该文引入符合边界条件(1)和边界条件(2)的线性损伤函数x(N)如下:
(6)
将受压疲劳边界条件代入混凝土受压疲劳剩余强度包络线方程(3),整理可得受压疲劳时x(Nf)方程为:
σmaxαc[x(Nf)]2+(σmax-fc-2σmaxαc)·[x(Nf)]+σmaxαc=0
(7)
求解方程(7)得到混凝土受压时x(Nf)为:
x(Nf)=
(8)
同理,根据受拉疲劳边界条件与混凝土受拉疲劳剩余强度包络线方程(4),可得受拉疲劳时x(Nf)方程为:
σmaxαt[x(Nf)-x(1)]1.7+(σmax-ft)x(Nf)=0
(9)
求解方程(9)可得到混凝土受拉时x(Nf)。
参数αc、αt按单轴受压(拉)应力-应变曲线软化段形状系数取值。
综上所述,将式(6)所示的线性损伤函数x(N)代入式(5),最终得到经历任意次数疲劳荷载后混凝土剩余强度为:
(10)
1.4 混凝土疲劳剩余强度验证
该文用文献[8]试验数据对混凝土疲劳剩余强度公式(10)进行了验证。文献[8]中共14组试件,7组用来做抗压,另外7组用来做抗拉,混凝土强度C30,试验情况与试验结果如表1所示。
用式(8)计算在0.75fc=18.35 MPa与0.85fc=20.80 MPa下的x(Nf)的值分别为1.632 7、1.436 6。抗压强度初始值σ0取表1中试验平均值 24.47 MPa,αc参照规范表C.2.4取1.36,计算得的剩余强度衰减规律见图2。
用式(9)计算在0.75ft=2.02 MPa与0.85ft=2.29 MPa下的x(Nf)的值分别为1.274 8、1.220 8 MPa。抗拉强度初始值σ0取表1中试验平均值 2.692 MPa,αt参照GB 50010-2010《混凝土结构设计规范》表C.2.3取2.81,计算得的剩余强度衰减规律如图3所示。
从图2得到:循环开始,混凝土抗压强度为初始强度24.47 MPa,疲劳破坏时剩余强度20.799 5 MPa[图2(a)]、18.352 5 MPa[图2(b)],都为疲劳荷载上限应力。从图3得到:循环开始,混凝土抗拉强度为初始强度2.692 MPa,疲劳破坏时剩余强度为2.019 MPa[图3(a)]、2.282 2 MPa[图3(b)],也都为疲劳荷载上限应力。计算与试验吻合,不但满足边界条件,也符合混凝土剩余强度退化规律。
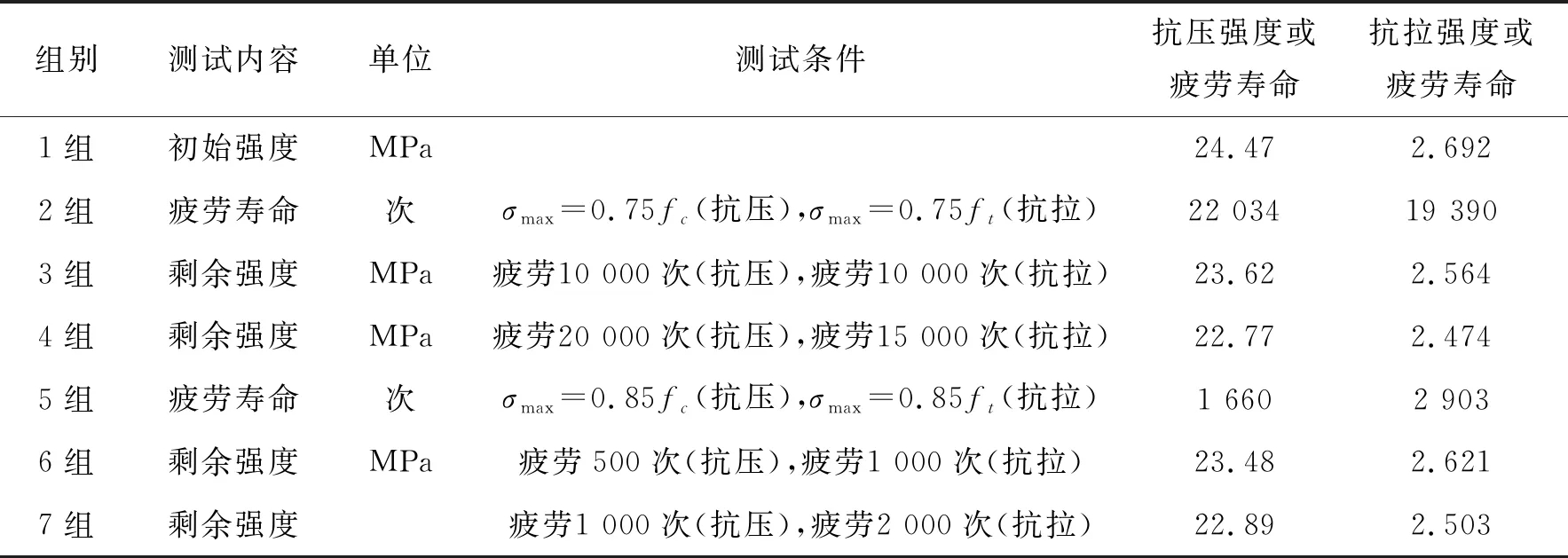
表1 混凝土疲劳剩余强度试验结果

图2 混凝土抗压疲劳剩余强度衰减规律
为了进一步比较结算结果与试验结果,验证以上提出的方法,该文将试验中测得的疲劳剩余强度和该文方法计算值进行了比较,结果如表2所示。从表2可以看出计算值与试验值(各组构件平均值)非常接近。
2 钢筋疲劳剩余强度计算
2.1 钢筋疲劳剩余强度推导
在推导钢筋的疲劳剩余强度及包络线方程过程中,运用了钢筋疲劳破坏的“二元判据”和其有效截面积非线性缩减的假定:
(1) 因为受疲劳荷载作用时,钢筋变形绝大部分是弹性变形,所以假定其弹性模量在整个疲劳过程中不变化。
(2) 假定受疲劳荷载作用后,钢筋的有效截面积非线性缩减。
(3) 在疲劳过程中,钢筋静拉伸强度不断衰减,当剩余强度下降到疲劳上限应力时发生静载瞬断的破坏,其失效符合“二元判据”,破坏准则为:
S≤σmax=σmin+Δσ
(11)
式中:σmax为当前应力最大值;S为计算得到的钢筋剩余屈服强度或剩余极限强度。
“二元判据”[式(11)]指明:钢筋疲劳破坏由钢筋当前应力和损伤共同确定,应力确定时损伤决定钢筋是否破坏,反之损伤确定时应力决定钢筋是否破坏。
该文基于上述3点假设,推导了钢筋在疲劳荷载作用下的剩余强度包络线方程,并获得了其经历任意次数疲劳加载后的剩余强度。推导如下:
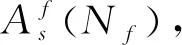
(12)
经Nf次等幅疲劳荷载作用,面积减少如下:
(13)
在疲劳过程中假设钢筋截面面积以非线性函数f(N/Nf)所示规律进行退化,对函数f(N/Nf)分析后发现有如下特点:
(1) 当N=0时,f(N/Nf)=0;即施加疲劳荷载之前,钢筋截面面积等于初始值A=As。

(3)f(N/Nf)为单调减函数,值域在0~1之间,即0≤f(N/Nf)≤1。
参照文献[13]的成果,f(N/Nf)可取f(N/Nf)=(N/Nf)c,c为钢筋材料的常数;则经历N次疲劳荷载,钢筋截面面积变为:
(14)
经历N次疲劳加载,钢筋损伤为:
(15)
由钢筋强度定义的损伤为:
(16)
由式(16)得到:
fy(N)=fy-D(N)·fy
(17)
钢筋截面面积的损伤和强度损伤一致,将式(15)代入式(17)后得到:
(18)
式(18)即为求解钢筋剩余强度的方程。从式(18)可得,只需知道疲劳寿命Nf及当前钢筋应力最大值σmax就可得到疲劳荷载作用N次后的剩余强度。σmax(Nf)=σmin+Δσ,依据钢筋强度退化表达式(18)可得疲劳荷载作用下钢筋剩余强度包络线方程为:
(19)
2.2 钢筋疲劳剩余强度验证
为了验证该文提出的方法,采用文献[14]试验进行了验证,并与李莉指数退化模型、苏志霄对数退化模型、谢里阳线性退化模型等已有常见模型进行了对比分析。试验采用35CrMo圆柱形钢,应力比R=-1,应力幅值σa=367 MPa,频率184 Hz,得到平均寿命Nf=1 151×103次,抗拉极限强度σb=1 000 MPa,屈服强度fy=780 MPa。还测得循环比为0.5、0.7与0.8时的钢筋剩余抗拉强度分别为979.33、965.85、940.07 MPa。该文模型中c值参考Schaff J(文献[17])研究成果取10.506。
该文方法得到的抗拉极限强度与屈服强度退化规律与其他模型规律如图4、5,其中Δσ=367 MPa,疲劳寿命为1 151×103次。
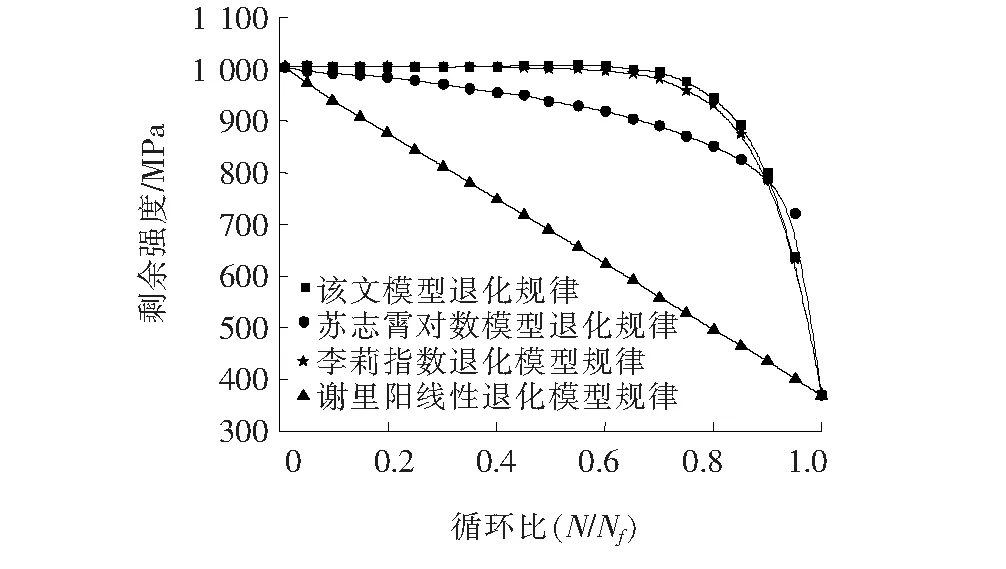
图4 钢筋疲劳抗拉极限剩余强度退化规律图
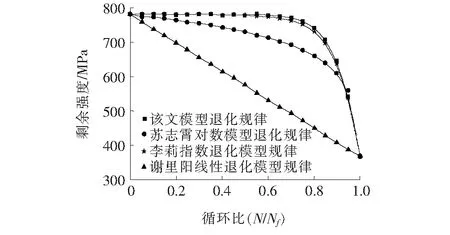
图5 钢筋疲劳抗拉屈服剩余强度退化规律
从图4、5得到:疲劳开始钢筋强度为1 000 MPa(或者780 MPa),即试验抗拉极限强度(或屈服强度),当疲劳破坏时,剩余强度为367 MPa,即最大循环应力(该文加载应力幅值)。说明该文方法也符合边界条件。比较各个模型看出:苏志霄模型只符合破坏“一元判据”,并且退化规律与实际也相差较大。谢里阳模型结果最为保守,可看做是对各非线性的近似处理。该文提出的模型计算分析结果与李莉模型计算分析结果最为相近,既符合“二元判据”,又比较接近实际衰退规律。
将循环比为0.5、0.7、0.8的剩余强度试验数据与各模型计算分析值进行比较,如表3所示。从表3看出:该文模型计算结果比较接近试验值。

表3 钢筋疲劳剩余强度计算值与试验值对比
3 钢筋混凝土梁基于材料强度疲劳耗散的承载力退化计算模型
3.1 承载力退化计算模型
GB 50010-2010《混凝土结构设计规范》进行钢筋混凝土梁正截面抗弯承载力计算时做了如下假定:(a)截面应变应该保持平面;(b)不考虑混凝土的抗拉强度;(c)将截面混凝土应力等效简化为矩形。基于上述假定,按照下式进行静载作用下钢筋混凝土梁抗弯承载力计算:
(20a)
Mu=Tuh0(1-0.5ξ)
(20b)

基于静载下的抗弯承载力计算基本假定(a)、(b),该文在进行钢筋混凝土梁疲劳抗弯承载力计算时还做了以下假定:
① 截面受压混凝土的应力呈三角形。
② 混凝土与钢筋的疲劳剩余强度按照该文推导公式(10)与(18)进行衰减。
因此,按照该文计算假定(a)、(b)、①、②、③,疲劳荷载作用下的混凝土剩余强度计算表达式(10),疲劳荷载作用下的钢筋剩余强度计算表达式(20),可得到疲劳荷载作用下钢筋混凝土梁的抗弯承载力计算模型如下:
(21a)
(21b)
式(21)即为钢筋混凝土梁基于钢筋与混凝土材料强度疲劳耗散的承载力退化计算模型。
3.2 承载力退化系数
受到疲劳荷载作用结构承载力下降的本质是材料强度的耗散衰减。如果仅考虑混凝土强度疲劳耗散,梁的抗弯承载力退化系数λ1可按下式计算:
(22)

综合式(10)、(20)与(21),λ1可写成:
λ1=
(23)
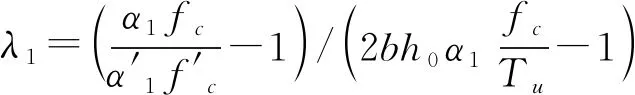
(24)
如果仅考虑钢筋强度疲劳耗散,梁的抗弯承载力退化系数λ2可如下计算:
(25)
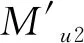
综合式(18)、(20)与(21),λ2可写成:
λ2=
(26)
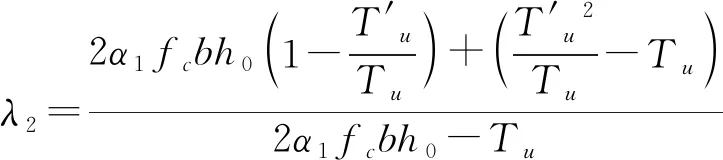
(27)
当同时考虑钢筋与混凝土材料强度的疲劳耗散下降,梁的抗弯承载力退化系数λ可如下计算:
(28)

综合式(10)、(18)、(20)与(21),λ可写成:
λ=
(29)
即:λ=
(30)
4 算例分析
算例采用钟铭试验数据与成果,用该文所推导的方法从材料强度疲劳耗散下降的角度对疲劳荷载作用下钢筋混凝土梁的承载力退化情况进行分析。其试验有13根梁,其中9根为高强度梁,4根为普通强度梁,尺寸为b×h=184 mm×214 mm,两种情况下的材料参数如下:
① 混凝土C40,fc=36.8 MPa,纵筋直径d=12 mm、Ⅱ级钢筋,纵筋屈服强度fy=445 MPa。
② 混凝土C70,fc=60.2 MPa,纵筋直径d=12 mm、新Ⅲ级钢筋,纵筋屈服强度fy=660 MPa。
①、②两种情况下混凝土保护层厚度均为c=30 mm,疲劳试验的最大荷载水平Smax=Mmax/Mu=0.4。试验应力幅度σr=σmax-σmin=169.82 MPa。由式(7)计算混凝土强度在fc=36.8 MPa与fc=60.2 MPa且在该文最大应力水平下的x(Nf)值分别为2.35、2.05 MPa。强度为C40混凝土的系数αc按照文献[12]中附录表C.2.4为1.94,同理查表得到强度为C70混凝土的系数αc为3.50。

当同时考虑两种材料强度的疲劳耗散下降,经过计算得到的钢筋混凝土梁抗弯极限承载力绝对量的衰减如图6所示。

图6 抗弯极限承载力绝对量的退化情况
图6表明:高强度混凝土梁的抗弯极限承载力要比普通混凝土梁的抗弯极限承载力大很多。两种梁的抗弯极限承载力随着疲劳循环次数的增加而发生退化,疲劳开始时退化量相对较小,中间大部分时间都保持线性变化,到循环比超过0.8时退化急速增加,在这个过程中两种梁的退化规律一致。
如果不考虑钢筋强度的疲劳耗散,其强度都取为①的情况,即fy=445 MPa,只考虑混凝土材料强度的耗散,对混凝土强度在C40与C70两种情况下的钢筋混凝土梁抗弯极限承载力进行计算,其退化系数λ1变化如图7所示。
图7表明:不考虑钢筋,只考虑混凝土材料强度的疲劳耗散,钢筋混凝土梁在两种情况下的退化系数λ1随循环次数增加都在增大,说明抗弯极限承载力都在下降,并且从计算结果可以看出高强混凝土梁的退化系数相比普通混凝土梁的退化系数增长慢,说明高强混凝土梁的抗弯极限承载力在疲劳过程中退化慢。
如果不考虑混凝土强度的疲劳耗散,其强度都取为①情况,即fc=36.8 MPa,只考虑钢筋材料强度的耗散,对钢筋强度在fy=445 MPa与fy=660 MPa两种情况下的钢筋混凝土梁抗弯极限承载力进行计算,退化系数λ2变化如图8所示。
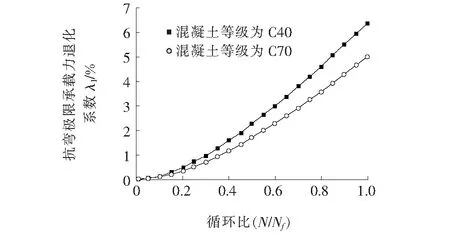
图7 退化系数λ1变化规律
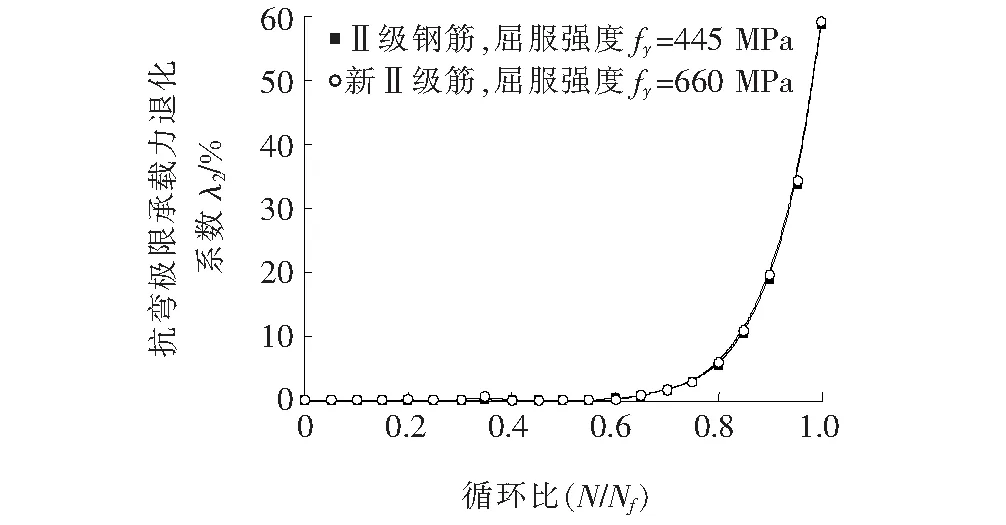
图8 退化系数λ2变化规律
图8表明:不考虑混凝土,只考虑钢筋材料强度的疲劳耗散,钢筋混凝土梁的抗弯极限承载力退化系数λ2起初变化较小,当循环比超过0.6以后迅速增大。说明钢筋强度的疲劳耗散对梁抗弯极限承载力的影响起初较小,但疲劳后期较大,并且钢筋屈服强度差异对梁抗弯极限承载力退化影响不明显。
如果综合考虑两种材料的疲劳耗散,对①、②两种情况下的钢筋混凝土梁抗弯极限承载力进行计算,其退化系数λ变化如图9所示。
图9表明:同时考虑两种材料疲劳耗散以后,梁的抗弯极限承载力系数λ先是较为缓慢地线性上升,循环比超过0.8以后迅速上升,说明梁的抗弯极限承载力先是较为缓慢的线性下降,接近破坏时再迅速下降,与图6得到的承载力绝对退化量一致。

图9 退化系数λ变化规律
5 结论
(1) 通过分析混凝土材料疲劳剩余强度退化规律和边界条件,将混凝土在单轴静载下应力-应变模型软化段曲线作为疲劳荷载作用下材料破坏时的剩余强度包络线,推导任意次数疲劳加载后的剩余强度包络线方程,通过求解此方程可以得到加载任意次数后的混凝土疲劳剩余强度。试验验证分析结果表明该文公式计算值与试验值吻合,不但满足边界条件,也符合混凝土剩余强度退化规律。由钢筋与混凝土两种材料组成的各式各类构件,在其疲劳荷载作用下的损伤、刚度、强度及承载力计算中,可用该文提出的混凝土疲劳剩余强度公式。
(2) 通过分析疲劳荷载作用下钢筋混凝土梁内钢筋剩余强度退化规律和边界条件,基于钢筋弹性模量不变、有效截面积非线性缩减、疲劳失效的“二元判据”等假定推导了钢筋在疲劳荷载作用下的剩余强度包络线方程,并获得其经历任意次数疲劳加载后的剩余强度。试验验证分析结果表明该文提出的模型计算分析结果既符合“二元判据”,又比较接近实际衰退规律。
(3) 基于推导的钢筋与混凝土材料的疲劳剩余强度,该文将静载与疲劳荷载作用时钢筋混凝土梁的抗弯极限承载力计算理论进行融合,提出钢筋混凝土梁基于材料强度疲劳耗散的承载力退化规律模型,并定义单一材料因素及两种材料综合影响下的承载力退化系数,并用算例进行验证。

