基于精细积分算法的混凝土路面层状结构动力响应求解与分析

张宇， 杨林青

(1.河南省收费还贷高速公路管理中心航空港管理处, 河南 郑州 450019；2.广东技术师范学院 天河学院)

1 前言

随着中国经济的不断发展，混凝土路面在中国得到越来越广泛的应用。近年来，在中国高等级公路建设中，混凝土路面已经成为其路面主要结构形式之一。但随着公路交通量的飞速增长，以及车辆大型化和严重超载等现象的增多，车辆增多、超载和超速等问题开始变得日益严重，越来越引起了人们对道路安全问题的关注。路基是路面结构的支撑体，经常出现的路面损坏现象大都是路基稳定性差、强度不足、在外荷载作用下导致过量变形所致。合理地选择路基施工措施是获得坚实而又稳定的路基、保证路基路面整体具有良好使用性能的关键。而构建沥青混凝土路面结构在动荷载作用下的精确高效数值模型一直是路面结构体系设计参数反演理论与技术研究的核心内容之一。正演算法还是依据路面实测数据进行反演得到地下结构层设计参数的前提，精确高效的正演模型对于提高反演精度和效率具有重要意义。

因为路面所受的荷载主要是来自于汽车的运动荷载，对道路工程的动力响应问题已经引起人们足够重视，随着FWD的广泛应用，为了通过反演计算得到路面结构的参数，出现了许多计算路面弯沉的正演方法，但是大部分计算方法是把外力当成静荷载来计算弯沉盆的最大位移。由于用落锤式弯沉仪测定路面的力学响应是在动态荷载脉冲的作用下，并且路面结构，特别是沥青路面面层在高温时呈黏弹性，如果对这种路面结构仍采用静荷载作用下弹性层状理论，计算结果必然与实际结果有较大误差。

随着计算机技术的飞速发展，越来越多的学者关注在动荷载作用下混凝土路面的动力响应问题。虽然有限元方法可以模拟复杂的路面结构，但是其计算效率和精度严重受网格的影响。Al等开发了一种精确的、计算独特的分析层状介质动态特性的正演算法，研究了路面在落锤式弯沉仪(FWD)荷载脉冲作用下的响应情况；Simon等提出了一种基于谱单元法的动态分析方法来解释柔性路面的落锤式弯沉仪(FWD)试验。

近年来精细积分算法被广泛应用到层状介质动力响应求解中。方宏远等采用基于两端边值问题的精细积分方法，分析了电磁波在层状有耗介质中的反射与透射问题，把控制方程按边值问题求解，可以避免在运算过程中出现指数矩阵相乘的大数溢出问题，将数值计算结果与广义传播矩阵方法加以对比；Lin等和Han等运用精细积分算法求解得到了层状地基上任意形状基础动力响应。该文基于传统谱单元方法，引入精细积分算法代替传递矩阵算法求解路面层状结构波数域内的动力位移响应，从而建立路面层状结构在FWD荷载作用下的动力响应求解精确算法。通过与已有算法数值结果的对比验证该文算法的准确性，在此基础上针对路面层状结构的杨氏模量以及厚度进行广泛的参数分析，以期为工程实际提供可靠的理论和数值基础，为路面结构设计和后期的维护方案选择提供指导帮助。

2 问题描述

在各种无损检测方法中，落锤式弯沉仪因其具有类似于卡车车轮施加的高振幅动态载荷的能力，已成为测量路面挠度最广泛使用的技术。FWD通过在0.3 m直径的圆形板上从特定高度扔下一个落锤，对路面产生冲击载荷。撞击产生的波在路面系统中传播，由此产生的挠度由n个检波器在距离圆形板中心D的地方测量。利用FWD对瞬态载荷和挠度进行监测，测量弯沉盆中心点的位移响应。

在路面层状结构的表面半径为a的圆形区域上施加瞬态荷载Q(t)，采用柱坐标系下的轴对称几何形式可以较好地反映FWD测试的力学几何特性。该路面由多层具有有限厚度hi的水平层以及底部均质半无限空间组成，每层介质均为均质弹性各向同性属性。

柱坐标系下轴对称问题的动力平衡方程如下：

(1)

式中：u(r,z,t)和w(r,z,t)分别为径向和竖向位移；σr(r,z,t)、σθ(r,z,t)和σz(r,z,t)分别为径向、切向和竖向正应力；τrz(r,z,t)为竖直面的切应力；ρ为介质的质量密度。

几何方程可以表示为：

(2)

式中：εr(r,z,t)、εθ(r,z,t)和εz(r,z,t)分别为径向、切向和竖向正应变；γrz(r,z,t)为竖直面的切应变；wθ(r,z,t)为切向转动分量。

应力-应变关系可以表示为：

(3)

式中：e(r,z,t)=εr(r,z,t)+εθ(r,z,t)+εz(r,z,t)；λ=2vG/(1-2v)，G=0.5E/(1+v)；E、ν和G分别为弹性模量、泊松比和剪切模量。

3 势能方程

在亥姆霍兹分解中，材料的位移场表示为标量势φ的梯度和矢量势ψ的旋度之和，如式(4)所示：

u=φ+×ψ

(4)

在轴对称运动中，矢量势ψ只有一个分量ψθ。这个性质把问题的解简化为只对标量势的解。为了方便标记，用ψ代替ψθ。同样，由于轴对称，θ方向的位移分量等于零。用u和w分别表示r和z方向的位移分量，位移分量与势的关系由式(5)、(6)表示：

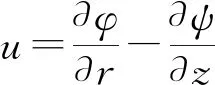
(5)

(6)

将式(5)、(6)代入式(2)，并结合式(1)、(3)可得：

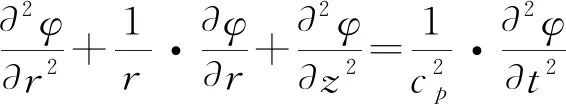
(7)

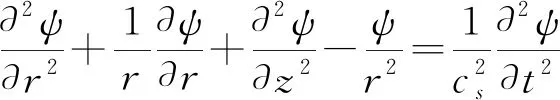
(8)

式中：常数cp=[(λ+2G)/ρ]1/2为压缩波速；cs=(G/ρ)1/2为剪切波速；式(7)、(8)为两种基本类型的波：压缩波(P)和剪切波(S)。

(9)

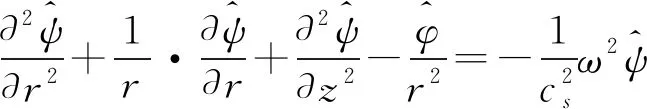
(10)

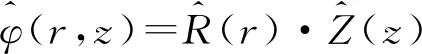
(11)

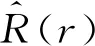
(12)

(13)

设s=kr，利用链式法则，方程(12)可归纳为贝塞尔方程：

(14)

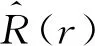
(15)

其中A1为边界条件确定的常数，k为径向波数。为了使问题离散化，引入径向边界条件是必要的。在径向边界r=R处(远离波源处)，认为振荡振幅消失。因此，式(15)的非平凡解变为：

(16)

这个条件可以满足于J0函数的无穷多个正根αm。式(16)表示kR=αm，因此k=km=αm/R。m函数表示为：

(17)

式(17)为波动在r方向上的解[方程(12)]，在r=R处消失。每个函数对应于第m个振型。这里可以注意到，r=R处的空间边界条件不可避免地导致一组离散的正常模态振动波数。

(18)

其中A2m为常数，由边界条件确定，i为复数，kpzmn为竖直方向的波数，表示为：

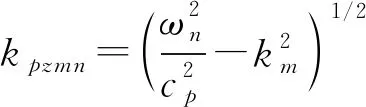
(19)

式中：cp为压缩波速；ωn为角频率。

因此，对于任意给定的角频率ωn，式(11)的解为：

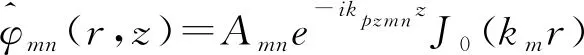
(20)

其中Amn为常数，由边界条件确定，J0为第零阶贝塞尔函数。

同理可以得到式(10)的解为：

(21)

4 波动问题的谱双重求和

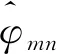
(22)

(23)

N和M的极限值可以由加载脉冲的时间和空间分布的振幅谱确定，对N个频率的求和可以使用快速傅里叶变换(FFT)，对M个波数的求和可以使用傅里叶-贝塞尔级数。傅里叶级数的双求和法是该方法相对于那些依赖于零到无穷积分的数值计算方法的一个重要的计算优势。如果系统没有阻尼或对于小阻尼有非常尖锐的峰值，那么这种集成将涉及奇点，并且需要相当长的计算时间和计算能力。

在得到φ和ψ的解之后，代入式(5)、(6)中可得轴对称介质表面位移表达式为：

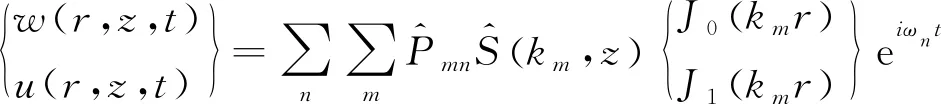
(24)

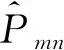
由式(24)可知：M个波数之和构成波的空间相依性(振荡形状)，N个频率之和构成波的时间相依性。

5 精细积分算法

精细积分是求解一阶常微分方程的高精度算法，已被应用于结构动力分析、控制论、波导等诸多领域。该方法通过将原有计算层厚度划分为2N1个子层，然后再将每个子层细分为2N2个微层，对于微层，由于其厚度非常小，其层间矩阵可利用幂级数展开求解。可以证明级数展开的截断误差低于计算机的舍入误差，从而得到几乎是计算机字节长上精确的数值解，并利用结构力学中的多层子结构算法对这些微段进行合并消元，在保证数值结果精度的前提下，大大提高运算效率。

5.1 区间矩阵初始化

选取微层的层间矩阵作为初始矩阵进行求解，利用如下公式计算系数矩阵：

(25)

其中：

(26)

层间矩阵F、G和Q由泰勒级数展开计算得到：

(27)

其中τ为微层的厚度，系数矩阵计算公式为：

θ1=-B,γ1=-D,φ1=A

(28)

(29)

(30)

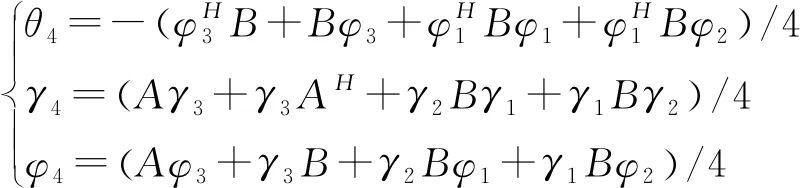
(31)

5.2 区间矩阵合并

首先对微层采用如下公式进行合并：

(32)

由于微层的区间矩阵相同，因此可以简单地对式(32)执行N2次合并循环即可得到子层的区间矩阵。

其次在得到子层层间矩阵的基础上，再采用如下公式对子层进行区间合并：

(33)

最后，在得到子层区间矩阵后，进一步针对不同材料属性的相邻层逐个进行合并，最终得到均质半无限地基之上的所有层的区间矩阵F、G和Q。

5.3 边界条件

得到所有层的区间矩阵F、G和Q之后，其上表面、下表面位移(q0和ql)和应力向量(p0和pl)之间的关系为：

(34)

其中：q0和p0分别为z=0处的位移向量和应力向量；ql和pl分别为z=l处的位移向量和应力向量。

对于层状地基底部(第l+1层)为刚性基岩的情况，需要满足第l层底部位移为0的边界条件，即：

ql=0

(35)

由式(34)得到路面位移与应力的关系：

p0=(Q+FG-1FH)q0=E(km)q0

(36)

对于层状地基下卧半无限空间的情况，需要考虑无限远处的辐射边界条件。均质半无限地基顶部位移和应力的关系为：

pl=R∞ql

(37)

式中：R∞为一个实对称矩阵，表示半无限空间的刚度矩阵，其计算可参见文献[12]。

由式(34)和式(37)对l层地基底部与半无限地基顶部进行组装，消掉ql和pl可以得到层状地基表面位移和荷载的关系为：

p0=(Q+R∞F(GR∞+I)-1FH)q0=E(km)q0

(38)

将式(36)、(38)中的E(km)求逆可得频率-波数域内层状地基表面在未知荷载作用下的位移为：

q0=S(km)p0且S(km)=E-1(km)

(39)

式中：S(km)中的元素即为方程(24)中的传递函数。

6 数值算例

6.1 算法验证

(1)R、M和N0的确定

式(24)中的双重求和积分涉及到上限的选取，为获得精确的结果，选取一路面结构，对参数R、M和N0的选取进行说明。路面结构包括3层，分别为混凝土面层、基层和底基层，其材料参数见表1，底部地基假定为均质半无限情况，其材料参数同样参见表1。

表1 混凝土路面结构和地基材料参数

利用该文提出的算法，选取如图1所示的荷载时程曲线作为FWD荷载，载荷幅值为40 kN，持续时间为30 ms，荷载作用于半径为0.15 m的圆形表面，即落锤的半径为0.15 m，计算落锤中心点处的弯沉点位移。

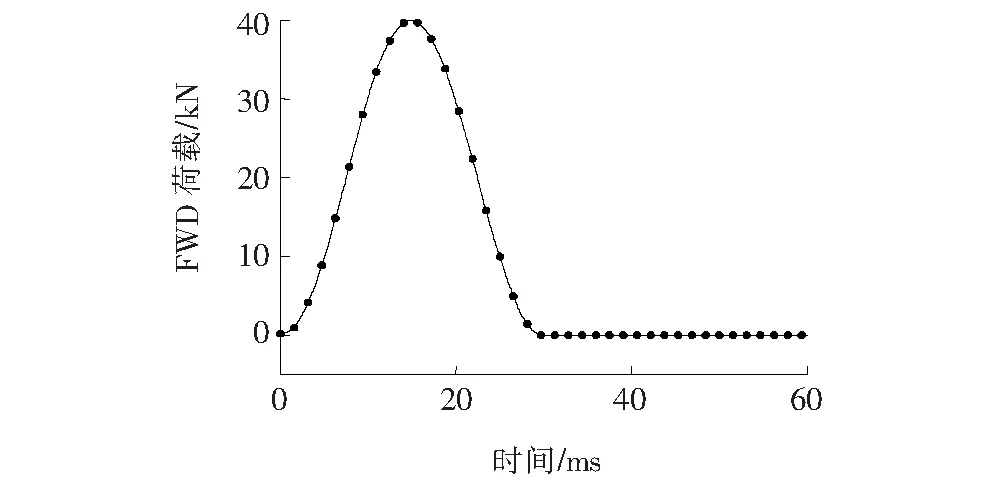
图1 FWD荷载时程曲线

首先说明式(16)中R的选取，其中Fourier变换样本数为N=2 048个，波数样本数M=1 500个，选取不同的R(R=1、10、30、50和60 m)分别进行计算，得到的落锤中心点位移时程曲线如图2所示。

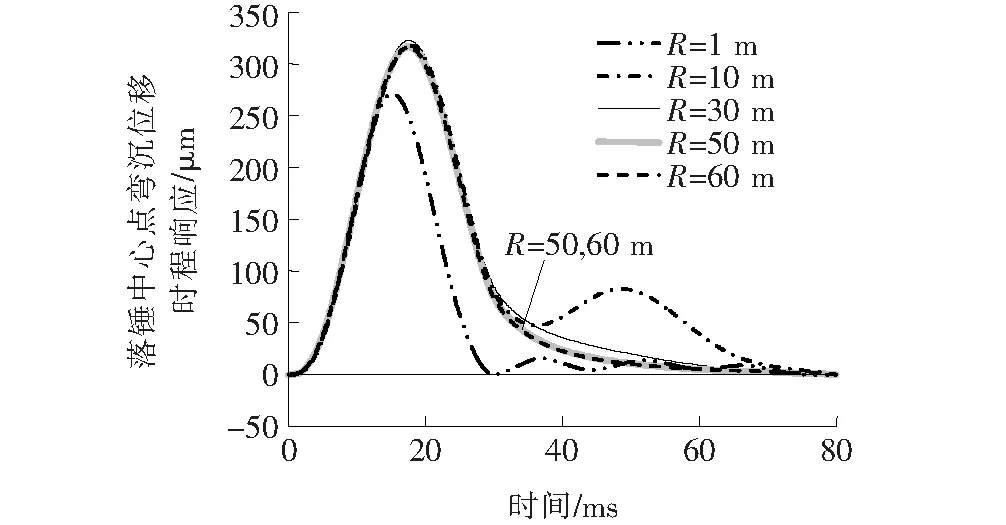
图2 参数R的确定

由图2可见：当R=50和60 m时得到的位移时程曲线基本相同，从而证明了双重求和积分对于R有良好的收敛性，在计算中可以选择有限的R进行计算。

其次针对M的选取进行说明，选取相同的路面结构模型进行计算，其中Fourier变换样本数为N=2 048个，R=60 m，选取不同数量的波数样本数M(M=100、500、800、1 000和1 200个)分别进行计算，得到的落锤中心点位移时程曲线见图3。

图3 参数M的确定

由图3可见：当M=1 000个和1 200个时得到的位移时程曲线基本相同，从而证明了双重求和积分对于M同样具有良好的收敛性，在计算中可以选择有限的波数样本数M进行计算。

最后，分析Fourier变换样本数中N0的选取。选取相同的路面结构模型进行计算，其中R=60 m，M=1 500个，Fourier变换样本数为N=2 048。值得注意的是，并不是所有的Fourier变换样本均需要计算，选择合适且有限的前N0个样本进行计算，不仅可以得到精确的结果，而且可以极大地提高求解效率。针对不同的N0(N0=10、50、80、120和150个)，计算得到的落锤中心点位移时程曲线如图4所示。

图4 参数N0的确定

由图4可见：当N0=120个和150个时得到的位移时程曲线基本相同，从而证明了双重求和积分对于N0同样具有良好的收敛性，在计算中可以选择有限的N0进行计算。

(2) 弯沉位移时程曲线验证

在验证双重求和积分参数上限的选取之后，选择合理的R、M和ωn即可得到高效而精确的结果。为验证该文算法对于不同距离点弯沉位移响应的准确性，选择与上例相同的路面结构和地基进行计算，取R=50 m，km=300，ωn=8 rad/s，计算距离落锤中心点距离为r=0、0.375、1和1.5 m位置弯沉点的位移响应，计算结果与文献[9]进行对比，如图5所示。

图5 该文算法结果与文献结果对比图

由图5可见：对于不同距离情况计算得到的弯沉位移，两者基本吻合，从而验证了该文算法的准确性。

6.2 杨氏模量E对路面结构动力响应的影响

路面结构杨氏模量是路面结构设计的一个重要指标，其值直接影响着道路的承受能力和使用寿命。为研究其对路面结构动力响应的影响，选取3层路面结构进行求解分析，包括混凝土面层、基层和底基层，地基假定为均质半无限空间，各层材料属性见表1。

(1) 面层杨氏模量

为分析混凝土面层杨氏模量对路面动力响应的影响，将面层的杨氏模量E分别减小50%、增大50%和增大100%进行计算，其他参数如表1所示。计算得到的荷载作用点的位移响应以及距离荷载作用点2.0 m内的位移响应最大值如图6所示。

由图6(a)可见：针对不同的杨氏模量E，位移时程响应出现最大位移的时间基本一致，而最大位移值变化较大，随着E的增大，最大位移出现明显的减小现象；由图6(b)可以看出：面层杨氏模量E的大小，虽然对荷载施加点的最大位移值影响较大，但对于距离大于0.5 m的位置影响变小，其影响范围为0～0.5 m。

(2) 基层杨氏模量

为分析基层杨氏模量对路面动力响应的影响，将基层的杨氏模量E分别减小50%、增大50%和增大100%进行计算，其他参数如表1所示保持不变。计算得到的荷载作用点的位移响应以及距离荷载作用点2.0 m内的位移响应最大值如图7所示。

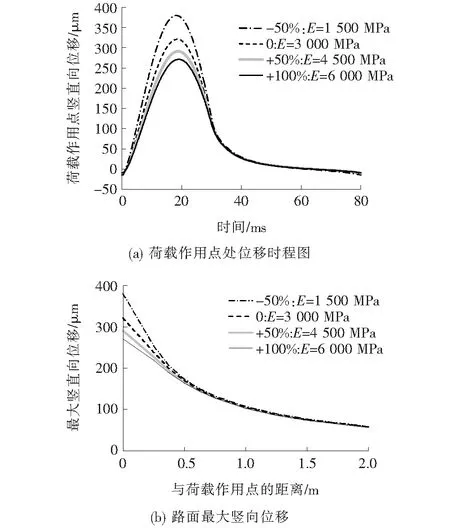
图6 面层杨氏模量对路面动力响应的影响

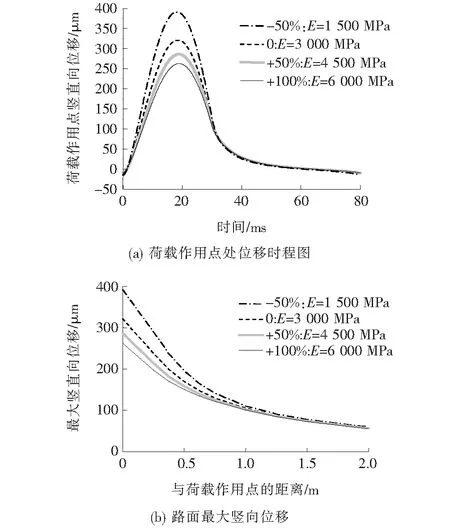
图7 基层杨氏模量对路面动力响应的影响

由图7可见：针对不同的杨氏模量E，其对路面结构动力响应的影响与面层基本相似，但是其影响的范围比面层更大，在距离荷载施加点0～1.0 m范围内基本都有影响，超过1.0 m范围影响较小。

(3)底基层杨氏模量

现把底基层的杨氏模量E分别减小50%、增大50%和增大100%。利用该文算法，求得路面结构动力响应荷载作用点处的位移时程响应及距离荷载作用点2.0 m内的位移响应最大值如图8所示。

图8 底基层杨氏模量对路面动力响应的影响

由图8可见：底基层杨氏模量的不同，对于弯沉位移时程曲线幅值的影响规律与面层和基层基本相同，但是其对最大位移值的影响范围更大，在0～2.0 m范围内，最大位移曲线基本发生了平移。

7 结语

基于传统的谱单元法，引入精细积分算法求解频率-波数域内弯沉点动力响应，进而求解路面层状结构在FWD荷载作用下的弯沉位移响应。该算法采用双重求和方式，选用有限的积分参数值代替无限积分，在保证精度的同时较大地提高了求解效率。通过数值算例验证了该文算法的准确性，在此基础上针对路面结构层的杨氏模量对路面弯沉点位移响应的影响进行了参数分析。结果表明：路面结构层的杨氏模量对弯沉点最大位移值有显著的影响，随着杨氏模量的增大，位移最大值明显减小；不同结构层对位移最大值的影响范围不同，面层影响范围较小，基层影响次之，底基层的影响范围最大。