时变因素影响下混凝土中氯离子扩散计算方法

孙红硕， 杨 格,2， 吴 斌

(1. 武汉理工大学 a. 土木工程与建筑学院；b. 硅酸盐建筑材料国家重点实验室，湖北 武汉 430070；2. 天津大学 中国地震局工程综合模拟与城乡抗震韧性重点实验室，天津 300350)

钢筋混凝土结构中氯离子的侵蚀是造成钢筋锈蚀的主要原因[1]。混凝土中氯离子的扩散过程可通过Fick第二定律来描述，通过氯离子扩散系数来反映混凝土中氯离子扩散的快慢。当混凝土所处的外部环境发生变化时，如温度、相对湿度等因素的改变[2,3]，以及混凝土本身的水化程度变化等[2]，都会导致混凝土中氯离子扩散系数随时间变化。此外，同一混凝土结构截面所受应力不同[4,5]、混凝土结构中的非贯通裂缝[6～9]等因素都会导致氯离子扩散系数随空间位置发生变化[10]。

Collepardi等[11]基于Fick第二定律计算了氯离子扩散方程的解析解，但其模型的氯离子扩散系数是定值，没有考虑随时间和空间的变化，计算结果与实际偏差较大。余红发等[12]采用随时间变化的氯离子扩散系数，其氯离子扩散系数模型考虑了混凝土龄期、温度等因素的综合作用，推导了氯离子扩散方程的解析表达式。Mejlbro等[13]考虑了混凝土龄期、养护条件、环境、温度等因素对氯离子扩散系数的影响，同样推导出了氯离子扩散方程的解析表达式。上述研究虽然给出了时变氯离子扩散系数下的扩散方程解析解，但其采用的温度、相对湿度等气候参数为恒定值，不符合实际情况。Hassan等[3]为研究气候变化对氯离子扩散的影响，通过蒙特卡罗采样获得每个月的温度和相对湿度值，并计算对应月份的氯离子扩散系数，然后采用有限差分法对混凝土中氯离子扩散进行模拟。但有限差分法在氯离子扩散系数变化速率较快时计算量非常大，不便于工程应用，而且现有氯离子扩散解析模型中扩散系数不能考虑温度、相对湿度等因素随时间变化的情况[2]。因此，需要建立任意氯离子扩散系数时变形式的解析模型，以便于考虑因温度、相对湿度等多种因素变化导致氯离子扩散系数随时间变化的情况。

在进一步考虑混凝土结构应力的不均匀分布和非贯通裂缝等因素导致氯离子扩散系数随空间变化的情况时，李镜培等[6]根据混凝土结构内裂缝的深度，将混凝土结构分为有裂缝区和无裂缝区，建立了考虑混凝土结构在非贯通裂缝条件下的氯离子扩散模型，但该模型无法考虑混凝土内氯离子扩散系数时变的影响。刘建文等[4]考虑了混凝土结构截面线性分布应力导致的氯离子扩散系数随空间的变化，同时也考虑了受混凝土龄期影响的氯离子扩散系数随时间的变化，建立了基于Fick第二定律的混凝土氯离子侵蚀模型，但该模型没有办法考虑温度、相对湿度等因素时变的影响。上述解析模型只适用于指定的氯离子扩散系数表达式，不适用于氯离子扩散系数随空间变化的其他形式，且不能考虑温度、相对湿度等因素时变的影响。Song等[14]为研究修复混凝土保护层对混凝土结构耐久性的影响，通过采用有限差分法中的Crank等[15]差分格式，计算了扩散系数随时间和空间同时变化的氯离子扩散过程。采用有限差分法能够同时考虑扩散系数随时间和空间变化的情况，但其在氯离子扩散系数变化速率较快时很难确定合理的时间步长，且计算量非常大，不便于工程应用。然而，在氯离子扩散系数随时间和空间均发生变化时，又很难实现建立适用于任意变化形式的解析模型。因此，需要高效简便的求解方法，以解决有限差分法在氯离子扩散系数变化速率较快时计算存在的问题。

为解决现有解析模型中氯离子扩散系数不能考虑温度、相对湿度等因素随时间变化的不足，本文通过理论推导建立了任意氯离子扩散系数时变形式的解析模型，该解析模型不仅能考虑混凝土龄期、氯离子结合能力和温度等因素的影响，而且还可以考虑温度、相对湿度等因素随时间变化的情况。为解决氯离子扩散系数关于空间、时间均发生变化时，扩散系数随时间变化较快会导致采用有限差分法计算量非常大，且很难确定合理时间步长的问题，本文提出采用等效氯离子扩散系数代替时变氯离子扩散系数方法。该方法可以避免采用有限差分法因扩散系数随时间的变化关系而减小时间步长的缺点，以解决有限差分法在氯离子扩散系数随时间变化较快时计算存在的问题。

1 氯离子扩散解析模型

当氯离子扩散系数为关于时间的函数时，基于Fick第二定律的氯离子扩散方程可表示为：

(1)

式中：C(x,t)为氯离子浓度，简写为C；t为结构暴露于环境中的时间；x为计算点距混凝土表面的深度；D(t)为任意时变形式的氯离子扩散系数；Cs为混凝土表面氯离子浓度；C0为混凝土中的初始氯离子浓度。

为了将式(1)化为常微分方程，引入ξ(x,t)(记为ξ)，并令

(2)

则有

(3)

(4)

(5)

将式(3)(5)代入式(1)，得

(6)

或

(7)

式(7)中的自变量只有唯一的ξ，于是便可将其写成如下常微分方程：

(8)

式(8)相应的初始条件和边界条件为：(a)ξ=∞时，C=C0；(b)ξ=0时，C=Cs。

现在求解式(8)，并使其满足初始条件(a)和边界条件(b)。令

(9)

将式(9)代入式(8)，得

(10)

将式(10)分离变量，积分得

P=U1e-ξ2

(11)

即

(12)

将式(12)进行积分，得

(13)

式中：U1，U2为积分常数，可根据定解条件(a)(b)确定。将边界条件(b)代入式(13)，得

(14)

进而得到

Cs=U2

(15)

将初始条件(a)代入式(13)，得

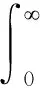
(16)

进而得到

(17)

将U1和U2代入式(13)，得

(18)

进而得到

(19)

即

(20)

式中：erfc(x)为关于变量x的互补误差函数。

式(20)即为本文提出的氯离子扩散解析模型。该氯离子扩散解析模型中氯离子扩散系数可为任意时变形式，以便于考虑温度和相对湿度等因素导致的氯离子扩散系数随时间变化的情况，实现对若干年后氯离子浓度分布的更精确预测。

为进一步验证本文提出的氯离子扩散解析模型的正确性，当模型仅考虑混凝土抗氯离子扩散的能力随时间增长逐渐增强的因素时，其t时刻的氯离子扩散系数可表示为[16]：

(21)

式中：Dref为参照氯离子扩散系数，即混凝土龄期t0(一般取28 d)时的氯离子扩散系数；m为扩散系数衰减率[12]。

将式(21)代入式(20)得

(22)

式(22)与文献[12]中解析解完全相同，验证了本文提出的氯离子扩散解析模型的正确性。

在本文提出的氯离子扩散解析模型中，氯离子扩散系数虽然可为任意时变形式，但并不适用于氯离子扩散系数随空间变化的情况。因此，当扩散系数随时间、空间均发生变化时，需要采用有限差分方法进行求解。

2 基于Crank-Nicolson有限差分格式计算变扩散系数的氯离子扩散

2.1 变扩散系数时的传统有限差分法求解

当扩散系数随时间、空间均发生变化时，基于Fick第二定律的氯离子扩散方程可以写成

(23)

该方程可采用Crank-Nicolson[15]有限差分格式进行求解。当距混凝土表面的最远计算距离为l，扩散总时长为tN时，计算t时刻距混凝土表面x处的氯离子浓度分布的方法如下：

(1)首先对时间和空间进行网格剖分，构造差分格式。其中剖分是将区域Ω={0≤x≤l,0≤t≤tN}用两簇平行直线

(24)

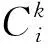
(2)采用有限差分法的Crank-Nicolson格式可表示为[14]：

(25)

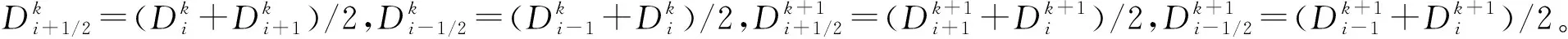
根据式(25)逐步计算即可得到整个扩散过程中的氯离子浓度分布，这一求解过程就是变扩散系数时的传统有限差分求解方法，后面简称为基于有限差分的传统方法。其中，在氯离子扩散系数为恒定值时，Crank-Nicolson格式的截断误差为o(τ2+h2)，因此需要限制步长以满足计算精度。另外，在扩散系数随时间、空间发生变化时较大步长会引入新的误差，往往需要更小的步长以减少因扩散系数随时间、空间发生变化引入的误差，当所取步长使得氯离子扩散系数在该步长内无变化可避免该误差。

2.2 基于等效氯离子扩散系数的有限差分法求解

通过式(20)可以看出，当不考虑氯离子扩散系数随空间变化时，在基于Fick第二定律的氯离子扩散模型中，随时间变化的氯离子扩散系数可由恒定的等效氯离子扩散系数代替，即：

(26)

将恒定的等效氯离子扩散系数Deq代替氯离子扩散系数D(x)代入式(1)，其计算结果与本文所提氯离子扩散解析模型计算结果一致，验证了上述方法的可行性。

前文介绍的有限差分法可以求解扩散系数随时间、空间均发生变化的情况，但通常需要较密的空间和时间网格划分，导致计算量较大。为了减少时间上的网格数，假定氯离子扩散系数随空间变化时也可采用等效氯离子扩散系数求解，本文拟采用等效氯离子扩散系数代替前文的变扩散系数。

假定氯离子扩散系数可表示为：

D(t,x)=F(t)G(x)

(27)

式中：F(t)为氯离子扩散系数中与时间相关的项；G(x)为与空间位置相关的项。

(28)

(29)

由于式(29)中的等效氯离子扩散系数与时间t无关，可以避免采用有限差分法因扩散系数随时间的变化关系而减小时间步长的缺点，以解决有限差分法在氯离子扩散系数变化速率较快时计算存在的问题。这一求解过程就是本文提出的基于等效氯离子扩散系数的有限差分求解方法，后面则简称为基于有限差分的简化方法。

3 算例与分析

3.1 算例一

广州某混凝土简支梁桥实心板，板厚280 mm。考虑到简支梁桥板服役状态，根据文献[17]假定板跨中截面受拉区最外侧拉应力水平为0.6，截面应力分布为线性分布，受拉区截面高度150 mm，仅考虑混凝土板跨中受拉侧氯离子一维扩散，如图1所示。参数取值：Cs=0.4%，C0=0，Dref=10-5.1mm2/s，m=0。以广州气候为例，广州多年1～12月份平均气温为14.0，15.7，18.5，22.8，26.0，27.8，29.1，28.8，27.5，25.1，20.3，15.7 ℃；平均相对湿度为64.7%，73.3%，75.7%，77.4%，75.7%，79.0%，72.7%，74.3%，70.7%，62.9%，63.4%，61.4%[2]。

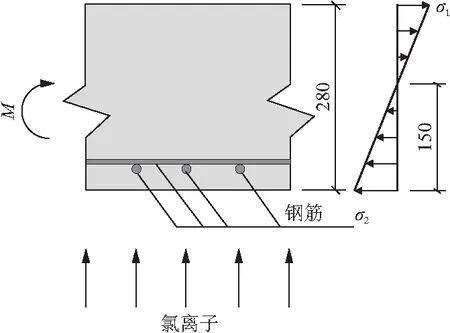
图1 氯离子侵蚀示意/mm

任心波[18]通过试验模拟海洋环境，给出了当荷载类型为受拉时，拉应力对混凝土的氯离子扩散系数影响关系为：

D(δ)=D(0)(1-0.11δ+2.93δ2)

(30)

式中：δ=σ/f，δ为应力水平，σ为混凝土截面所受应力，f为混凝土的强度。

根据拉应力对混凝土的氯离子扩散系数影响关系可得混凝土弯曲受拉侧扩散系数随深度变化函数为：

Dx=D0[1-0.11(0.6-0.004x)+

2.93(0.6-0.004x)2]

(31)

式中：x为距混凝土表面的距离；Dx为距混凝土表面x处的氯离子扩散系数；D0为混凝土表面处的氯离子扩散系数。则G(x)=[1-0.11(0.6-0.004x)+2.93(0.6-0.004x)2]。

根据本算例参数，并结合文献[19,20]中温度和相对湿度对氯离子扩散系数的影响关系，计算出不同时间的氯离子扩散系数值，假定该值为混凝土表面处对应时间氯离子扩散系数值D0(t)，则式(27)中F(t)=D0(t)。氯离子扩散系数D(t,x)=F(t)G(x)。其中每个月按30 d计算，分别采用基于有限差分的简化方法和基于有限差分的传统方法计算第3年末的氯离子浓度分布。其中，时间步长τ=86400 s，空间长度l=150 mm，空间步长h=1 mm。

采用基于有限差分的传统方法和基于有限差分的简化方法分别计算得到第3年末的氯离子浓度分布见图2。由式(25)可知，在每个计算步长内氯离子扩散系数无变化时，不会引入因氯离子扩散系数变化产生的误差，因此本算例中基于有限差分的传统方法计算不会引入因氯离子扩散系数随时间变化产生的误差。本算例以基于有限差分的传统方法计算结果作为参考解，基于有限差分的简化方法均方根误差为0.0000066052%，验证了基于有限差分的简化方法应用于扩散系数随时间、空间均发生变化情况的可行性。基于此可以推断出当扩散系数随时间、空间均发生变化时，该方法同样可以避免采用有限差分法因扩散系数随时间的变化关系而减小时间步长的缺点。

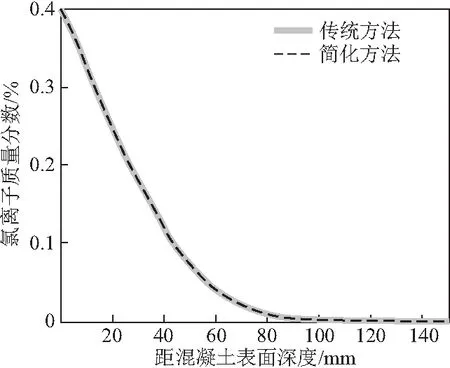
图2 氯离子浓度分布

本算例中均方根误差计算公式为：

(32)

式中：M为总空间点数；C(i)为第i个空间点的氯离子浓度值，Cref(i)为参考解的第i个空间点的氯离子浓度。

3.2 算例二

为分析在氯离子扩散系数随时间变化较快的情况下，基于有限差分的传统方法和基于有限差分的简化方法的计算量和计算精度。参数取值：Cs=0.4%，C0=0，Dref=10-4.1mm2/s。根据参数取值并考虑氯离子扩散系数衰减率m，可得第t时刻混凝土内氯离子扩散系数为：

(33)

通过第t时刻混凝土内氯离子扩散系数可以看出，氯离子扩散系数衰减率越大氯离子扩散系数随时间变化越快。其中，基于有限差分的传统方法，计算时间步长取2592000 s，m=0.64命名为组1；基于有限差分的传统方法，计算时间步长取1 s，m=0.64命名为组2；基于有限差分的简化方法，计算时间步长取2592000 s，m=0.64命名为组3；基于有限差分的传统方法，计算时间步长取2592000 s，m=0.2命名为组4。所有组中空间步长都取1 mm，分别计算第3年末混凝土内的氯离子浓度分布。以式(22)解析解为参考解，分别获得所有组计算结果的均方根误差(表1)。

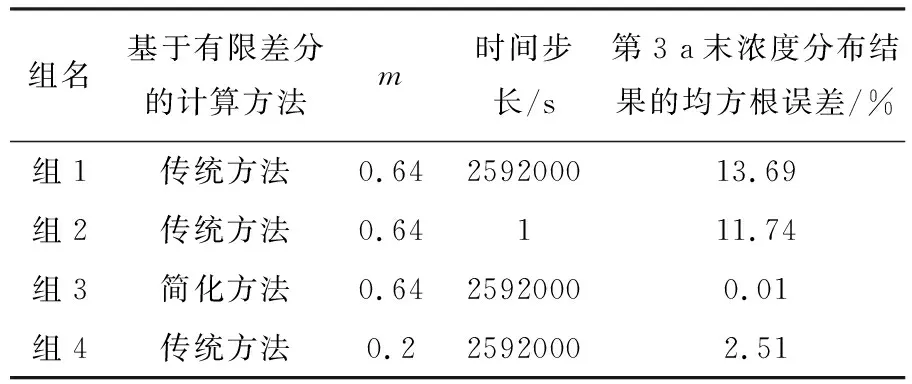
表1 氯离子扩散计算参数及氯离子浓度误差

通过组1和组4计算所取参数和结果均方根误差对比，相同时间步长下，氯离子扩散系数随时间变化快慢对基于有限差分法的传统方法计算精度影响非常大。通过组1和组2计算所取参数和结果均方根误差对比，当氯离子扩散系数随时间变化相对较快时，基于有限差分的传统方法通过减小时间步长虽然可提高计算精度，但是本算例中减少2592000倍的时间步长对精度提高并不显著。其中，组2通过R 2017b版本的MATLAB计算时间已超过24 h，计算机处理器为Intel(R)Core(TM)i7-8700CPU@3.20GHz，如果在m=0.64情况下，要保证计算的均方根误差达到5%以内，至少需要将1 s的时间步长减小上万倍，计算量非常大。因此在氯离子扩散系数随时间变化较快时，基于有限差分的传统方法为保证计算精度需要采用非常小的时间步长，会导致计算量非常大。并且由于没有氯离子扩散系数随时间变化速率与计算所需时间步长的精确关系，很难确定保证精度的合理时间步长。通过组1和组3计算所取参数和结果均方根误差对比，在氯离子扩散系数随时间变化较快时，同样步长下，基于有限差分的简化方法计算精度比基于有限差分法的传统方法计算精度高。这是由于氯离子扩散系数随时间变化越快，基于有限差分法的传统方法为保证精度计算所需要的时间步长越小，本文所提方法将随时间变化的氯离子扩散系数转化为恒定的氯离子扩散系数值，使得本文所提方法在不减少计算步长的情况下仍能获得较好的精度。验证了在氯离子扩散系数随时间变化速率较快时，本文所提方法一方面可避免基于有限差分法的传统方法为保证计算精度需要采用极小时间步长的问题，另一方面可避免基于有限差分法的传统方法为保证计算精度难以确定合理时间步长的问题。

4 结 论

(1)本文为解决现有解析模型中氯离子扩散系数不能考虑温度、相对湿度等因素随时间变化的不足，通过理论推导建立了基于Fick第二定律的氯离子扩散解析模型。该氯离子扩散解析模型中氯离子扩散系数可为任意时变形式，不仅能考虑混凝土龄期、氯离子结合能力和温度等因素影响，而且还可以考虑温度、相对湿度等因素随时间变化的情况。通过与现有氯离子扩散系数时变形式解析模型对比，验证了本文提出解析模型的正确性。

(2)当考虑因混凝土结构应力的不均匀分布和非贯通裂缝等因素导致的氯离子扩散系数同时随空间变化的情况，即氯离子扩散系数关于空间、时间均发生变化时，传统有限差分法存在难以确定保证精度的合理时间步长以及计算量大的问题。本文提出采用等效氯离子扩散系数代替时变的氯离子扩散系数，在不减小时间步长的情况下仍能获得较为满意的精度。通过算例一和算例二分别验证了该方法在氯离子扩散系数关于空间、时间均发生变化时的可行性，以及在计算氯离子扩散方面的优越性。