弯折贯穿钢筋PBL剪力键力学性能试验

黄彩萍， 游文峰， 谭金甲， 杨艳霜， 甘书宽

(湖北工业大学 土木建筑与环境学院，湖北 武汉 430068)

钢-混凝土组合结构由于施工方便、强度大、延性好、耐腐蚀等优点，在大型桥梁、建筑和某些特定结构中得到了广泛应用[1]。抗剪连接件作为组合结构中的重要构件，使钢构件与混凝土形成整体，协同工作，还能抵抗钢板和混凝土具有分离趋势的掀起力[2]。

因此，抗剪连接件的选择对组合结构中各材料的性能是否能够充分发挥起着至关重要的作用。PBL(Perfobond Leiste)抗剪连接件，又称开孔板抗剪连接件[3]，是由德国人Leonhardt和Parterners公司共同研发的一种连接件。它的特点是将开有一定数量孔洞的钢板焊接在钢构件上，再埋入混凝土当中，由开孔钢板和孔中混凝土榫共同抵抗剪力。研究人员发现，在孔中插入贯穿钢筋能有效提高该连接件的抗剪能力，因此在后期的桥梁工程应用中，多数PBL剪力键会设置贯穿钢筋。PBL剪力键因不受方向限制、承载力高、抗疲劳效果好等优点已于众多大型桥梁得到应用，我国南京长江三桥、广州新光大桥、重庆朝天门大桥均采用了该剪力键。

为了获得抗剪水平更加优秀的连接件，国内外学者纷纷对PBL剪力键进行改良，Kim等[4]提出了Y形开孔板连接件并对12个试件展开推出试验，结果表明增大贯穿钢筋的直径能提高连接件的抗剪能力且在低强度混凝土时提升效果较好；李淑琴[5]对18个开孔波折板试件展开推出试验，结果显示开孔波折板PBL连接件的承载力相对普通PBL连接件提高了38.8%；李帼昌等[6]对10个π形开孔板连接件试件分别进行单调推出和重复荷载推出试验，研究结果表明，贯穿钢筋的设置能使连接件的延性更好，减小腹板间距能提高连接件的承载力；Liu等[7]提出了一种橡胶环PBL连接件，讨论了不同橡胶环厚度对PBL连接件受力性能的影响，研究结果表明，橡胶环能提高PBL剪力键的滑移能力，降低其抗剪刚度，6 mm厚的橡胶环对滑移量的提升效果最好。

实际工程中PBL连接件的布置方式以群键为主，在一些钢板尺寸较为狭小，而传力需求较大的结构中，布置上述改良型PBL剪力键，可能出现施工空间不足、施工难度大、不能在满足构造要求的前提下焊接开孔板等问题。本文提出一种简单可行的改进方法，将普通直形贯穿钢筋弯折后，放入开孔板中，利用钢筋良好的抗拉性能，提高连接件的承载力。

多数学者[8～10]为详细研究PBL剪力键的受力机理，会在开孔板及贯穿钢筋上下表面黏贴应变片或三向应力花用以分析其应力应变关系。但应变片无法对试验加载全过程进行实时动态监测，且测点容易损坏导致部分测试数据失效。近年来，光纤光栅传感技术[11～13]被广泛应用于温度、应变、加速度等物理量的测试，它能对结构进行实时监测，弥补了传统应变片因测点损坏造成测试失效的缺陷。本文分别在两种不同形态的贯穿钢筋上布置光栅应变传感器，对加载全过程中贯穿钢筋的应变值进行动态监测，用以分析不同形态贯穿钢筋的力学性能差异。

1 试件设计

本文参考欧洲规范[14]设计并制作了6个弯折贯穿钢筋PBL推出试件和2个直形普通贯穿钢筋PBL推出试件，试件尺寸如图1，2所示。每个试件均由1个250 mm×200 mm×360 mm工字型钢、2块开有40 mm孔径的180 mm×60 mm开孔钢板、2根直径14 mm的贯穿钢筋、2块200 mm×320 mm×360 mm混凝土板组成，其中工字型钢与开孔板的厚度均为16 mm，弯折钢筋弯起方法为在距离钢筋端头5 cm处逆时针弯起45°，弯折长度23 cm，整个弯折钢筋呈反“Z”字形,。试件各材料的主要力学指标如表1所示。为避免混凝土发生脆性破坏，根据我国现行GB 50010—2010《混凝土结构设计规范》[15]按构造要求配置钢筋骨架。

表1 推出试件材料属性 MPa

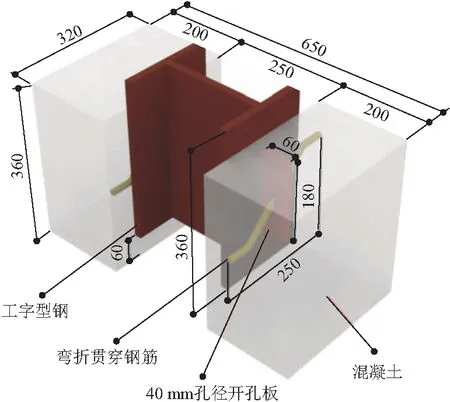
图1 弯折钢筋PBL试件构造/mm

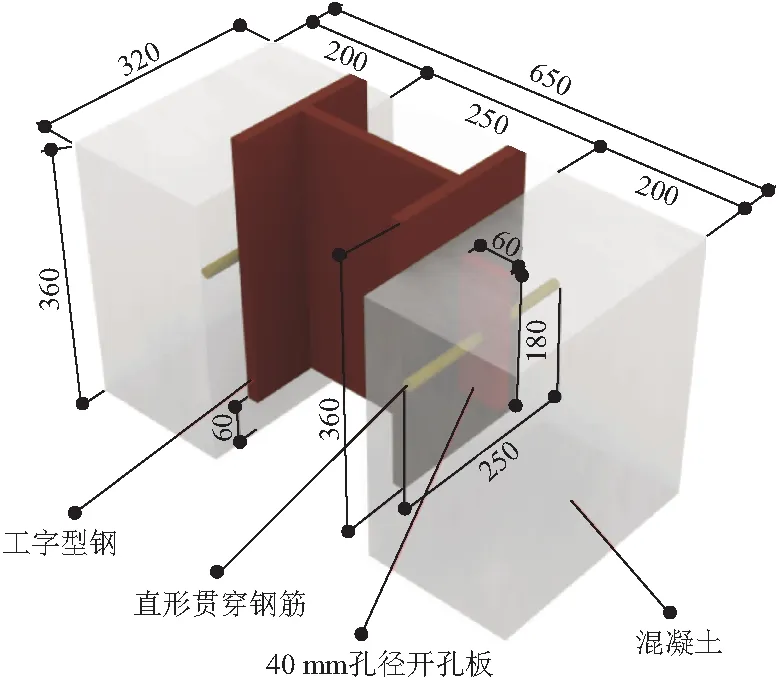
图2 直形钢筋PBL试件构造/mm

2 测点布置及加载方案

2.1 相对滑移量测点布置

剪力连接件连接钢构件和混凝土构件，如果钢-混结合面滑移量过小，结构可能因连接件的延性不足发生脆性破坏，而滑移量过大又会造成连接件抗剪刚度降低。因此型钢与混凝土的相对滑移量是考察连接件延性的一个重要指标。本文相对滑移量测点布置在钢-混结合面的中部，如图3所示。

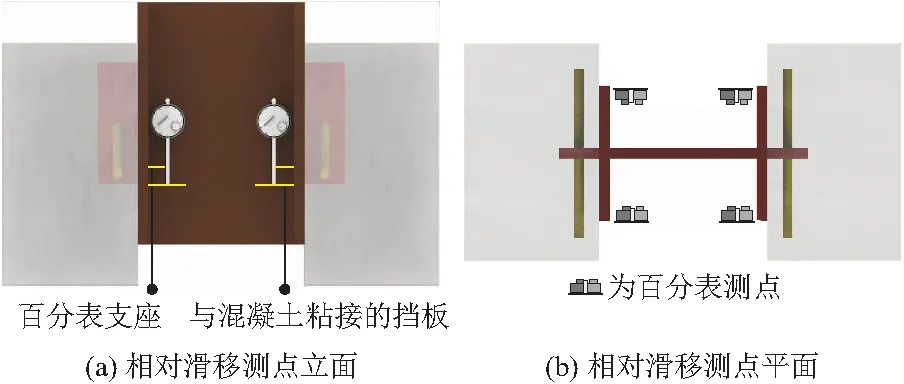
图3 相对滑移测点布置

2.2 应变测点布置

应变可以直接反映构件的受力状态。本文采用光栅应变传感器代替传统的应变片对两种形态的贯穿钢筋在加载全过程应变值进行动态监测。

如图4所示，在直形1号和弯折1～3号试件的贯穿钢筋上布置光栅传感器应变测点，两个底座焊接好后将光栅传感器安装于底座上，为保证测量的精确性，使用硬质PVC塑料对传感器进行封装，起到保护传感器和隔绝混凝土的作用，如图5所示。本文采用型号为JFSS-04的低温敏型光纤光栅应变传感器，中心波长1510～1590 nm，测量标距为60 mm，采用如图6所示的美国Micro Optics公司生产的SM-125解调仪，该解调仪的波长扫描范围满足要求，扫描频率为2 Hz，波长及应变的变化情况由配套计算机软件自动记录，无需人工读取，在加载全过程中，设定解调仪的解调频率为3次/min。

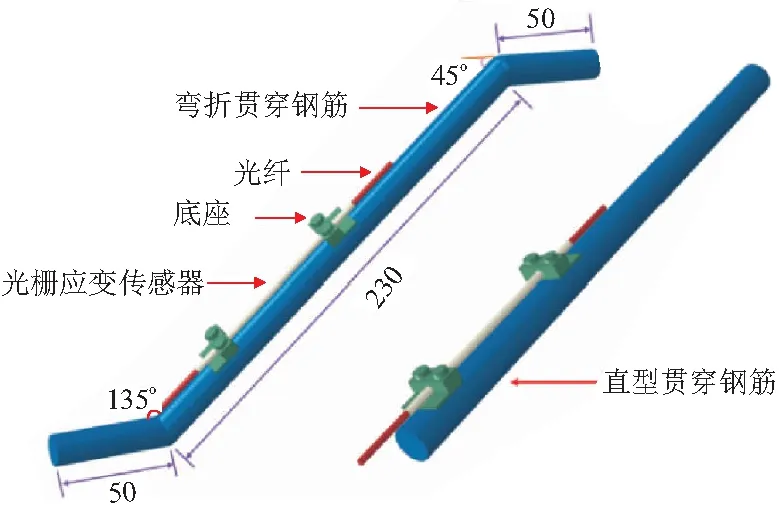
图4 光栅应变测点布置/mm

图5 光栅应变传感器封装

图6 SM-125解调仪

2.3 加载方案

推出试验在电液伺服压力试验机YAW-3000G上进行，利用垂线法及球角钢板对中调平。试验开始前以100 kN的预压荷载对试件进行预压，微调试件位置，当4个百分表读取的相对滑移量误差在±0.1 mm以内时认为试件处于轴心受压状态。

正式加载采用分级位移加载，设定加载速率为0.4 mm/min，每级位移荷载0.4 mm，持荷2 min。当加载位移达到4 mm后，为保证试验安全，调整加载速率至0.2 mm/min，每级位移荷载为0.2 mm，持荷2 min，直至试件破坏，试验加载如图7所示。

图7 试验加载过程

3 试验结果分析

3.1 试件破坏形态

(1)本次试验中，8个试件均是以混凝土严重开裂无法继续承载宣告破环的，此时试验机无法继续施加位移荷载停止试验。

(2)如图8所示，直形钢筋试件的主要破坏位置在混凝土顶面及侧面。试件破坏时，混凝土顶面出现较大横向裂缝并朝两侧延伸；底部混凝土因受到较大压力，从侧面开始出现竖向裂缝，并向上延伸。

图8 直形钢筋试件混凝土开裂部位

(3)弯折钢筋试件的主要破坏位置在混凝土顶面及钢-混结合面，如图9所示。混凝土顶部裂缝随荷载的增大只向单边延伸；结合面处混凝土出现斜向裂缝，最终剪切破环。

图9 弯折钢筋试件混凝土开裂部位

(4)试验加载结束后，对试件混凝土进行不同方向剖切，平行于开孔板的剖切面称为1-1，平行于贯穿钢筋的剖切面称为2-2，剖切部位如图10所示。

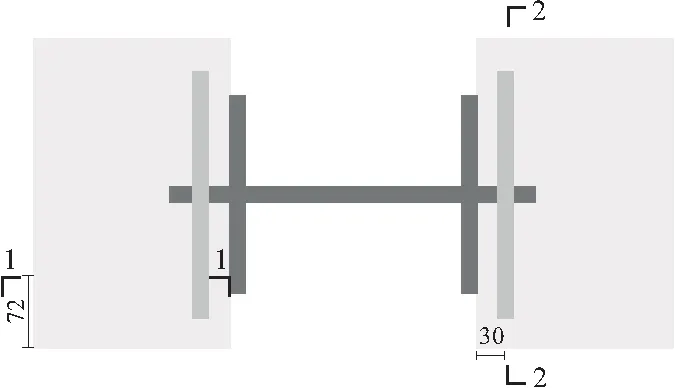
图10 剖切面示意/mm

直形钢筋试件的剖切面如图11所示。由图11a可见，混凝土底部先开始出现斜向裂缝，然后向上延伸，直至贯通；由图11b可见，开孔板下部混凝土已被割裂，位于开孔板两侧的混凝土开裂，呈剪压破坏，钢筋末端周围的混凝土出现斜向裂缝，直至贯通。

图11 直形钢筋试件混凝土剖切面

弯折钢筋试件的剖切面如图12所示。由图12a可见，混凝土底部出现斜向裂缝，但没有贯通；由图12b可见，开孔板底部的混凝土出现大面积破坏，但上部由于试件采用的是弯折钢筋，试件受力时，没有发生类似于直形钢筋试件的贯通裂缝。

图12 弯折钢筋试件混凝土剖切面

(5)凿开部分试件，取出开孔板中的贯穿钢筋。直形钢筋和弯折钢筋的变形对比如图13所示，两种钢筋没有发生过大的变形，在开孔板的位置有轻微弯曲，说明试件均是由于混凝土被剪切破坏而失效的。

图13 两种贯穿钢筋变形对比/cm

3.2 极限承载力

本次试验采用位移加载，试验机会自动换算每级位移荷载对应力的大小，本文取加载过程中试验机记录的最大剪力作为试件的极限承载力。由于每个试件中包含2个PBL剪力键，将试件所受最大剪力的1/2作为单个连接件的抗剪承载力。表2列出了本次试验8个试件的极限承载力及单个PBL剪力键的抗剪承载力。

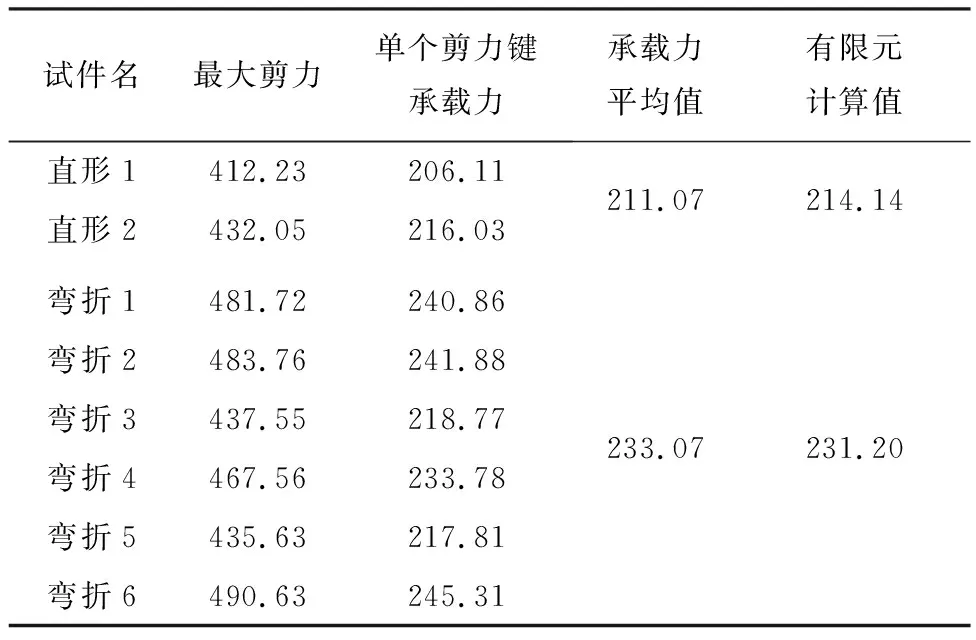
表2 试件承载力汇总 kN

由表2可见，弯折钢筋PBL剪力键的抗剪承载力为233.07 kN，较普通PBL剪力键提高了10.42%。表3列出了部分学者的试验参数及单孔PBL剪力键的抗剪承载力。由表3可见，本次试验所得PBL剪力键的抗剪承载力与其他学者的试验结果较为接近，试验效果良好。

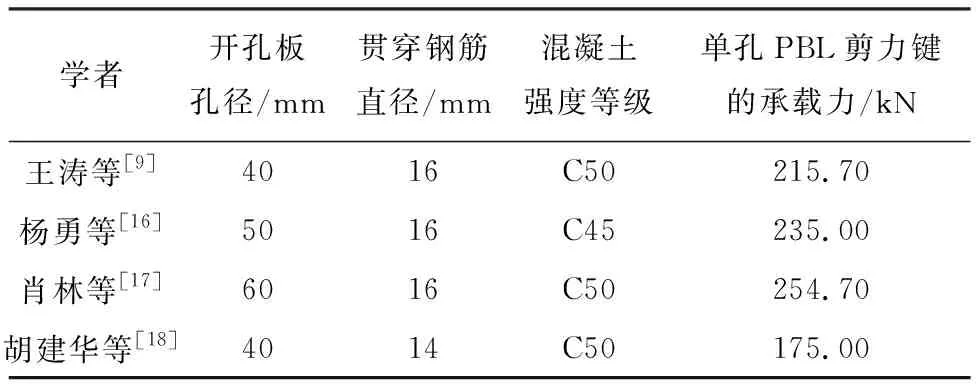
表3 部分学者试验参数及抗剪承载力汇总

针对含有贯穿钢筋的PBL剪力键，许多学者及国家规范均给出了抗剪承载力计算公式，我国学者胡建华等[18]基于自身推出试验，提出了以下计算公式：

(1)

式中：Qu为极限承载力；α取1.320125；β为普通横向钢筋影响系数，当横向钢筋的配箍率不大于0.18%时，β取1.204479，大于0.18%时，β取1.042948；Atr，A′tr为贯穿钢筋和普通横向钢筋截面面积；fy，f′y为贯穿钢筋和普通横向钢筋的抗拉强度；γ为构件系数，取1.95168；Asc为环形混凝土榫的面积；fc为混凝土立方体抗压强度。

Medberry等[19]考虑了型钢翼缘板与混凝土结合面的摩擦力，提出了以下计算公式：

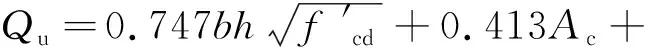
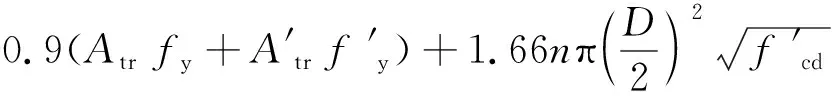
(2)

式中：b为混凝土厚度；h为开孔板下边沿至混凝土底部的距离；Ac为型钢翼缘板与混凝土的接触面面积；n为开孔数量；D为开孔板孔径；f′cd为混凝土圆柱体抗压强度。

文献[14]提出了以下计算公式：

(3)

式中：56×103≤A≤380×103；d为贯穿钢筋直径；γ一般取1.0。

文献[20]提出了下列计算公式：

(4)

式中：72.3×103≤A≤488.0×103；γb取1.3。

现将本次试验相关参数带入上述计算公式，得出PBL剪力键的抗剪承载力计算值，如表4所示。

表4 PBL剪力键抗剪承载力计算值汇总 kN

由表4可见，本次试验所得普通直形钢筋PBL剪力键的抗剪承载力与式(1)计算值较为吻合，与式(2)的计算值偏差较大。式(2)中钢-混结合面的摩擦力偏大，实际情况是结合面一旦出现分离，摩擦力几乎为0。而式(3)(4)没有考虑混凝土中普通钢筋的抗剪，计算得到的PBL剪力键抗剪承载力偏小。所以式(1)与实际情况较为相符，本文试验得到相关数据可靠。

3.3 荷载滑移曲线

本次推出试验钢-混结合面的相对滑移量取四个百分表读数(每级荷载读数减去初读)的平均值，8个试件的荷载-滑移曲线如图14所示。

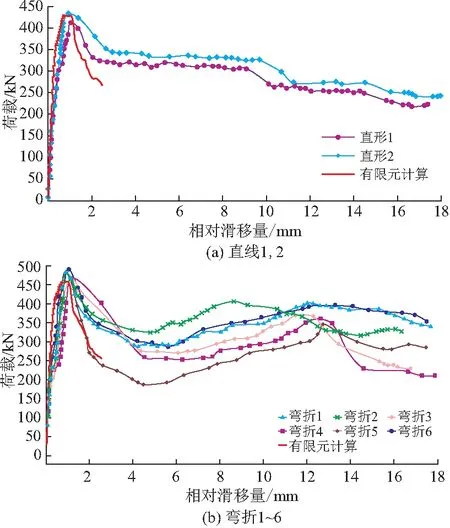
图14 荷载-滑移曲线

由图14可见：

(1)PBL剪力键的荷载-滑移曲线在弹性阶段的滑移量非常小，肉眼基本观察不出钢板和混凝土之间的相对滑移，达到最大承载力后，由于混凝土局部开裂，试件承载力迅速下降。

(2)8个试件的荷载滑移曲线在弹性阶段趋势基本相同。当荷载小于100 kN时，滑移量极其微小，这是由于结合面的粘结抵消了部分剪力。当结合面的粘结完全消除后，滑移量随着荷载的增大开始缓慢增加，直至达到最大承载力，但滑移量的增幅始终较小。

(3)弯折钢筋试件在进入塑性阶段后，荷载-滑移曲线出现了二次上升现象，直形钢筋在进入塑性阶段后，荷载-滑移曲线缓慢下降，没有再上升，说明弯折钢筋试件的承载力在达到极限后不会立即失效，有利于提高PBL连剪力键的延性。

3.4 抗剪刚度分析

对于抗剪刚度的定义，各国学者的方法有所不同。日本研究人员以荷载-滑移曲线中1/3极限荷载处的割线斜率作为抗剪刚度[21]；爱尔兰学者Ohelers基于大量的推出试验，以1/2极限荷载对应的割线斜率作为抗剪刚度；我国学者大多以滑移量为0.2 mm处的割线斜率作为抗剪刚度。本文依据上述三种抗剪刚度计算方法，分别计算每个试件中单个PBL剪力键的抗剪刚度，表5列出了两种贯穿钢筋PBL剪力键抗剪刚度的平均值。

由表5可见：

表5 PBL剪力键抗剪刚度汇总 kN/mm

(1)1/2极限荷载处的割线刚度明显小于其他两种计算方法得出的抗剪刚度，这是由于当剪力为极限荷载的1/2时，结合面的滑移量已相对较大，可以判定8个试件均已进入塑性阶段，所以此方法计算得到的是PBL剪力键在塑性阶段的抗剪刚度。

(2)当剪力为极限荷载的1/3时，此时钢-混结合面的粘结力还未完全消除，相对滑移量非常微小，所以此方法计算得到的是PBL剪力键在弹性阶段的抗剪刚度。

(3)当滑移量为0.2 mm时，荷载-滑移曲线的切线斜率与割线斜率之比约为0.5，可认为此处为曲线线性与非线性阶段的临界点，采用此处的割线斜率作为PBL剪力键的抗剪刚度较为合理，按此方法计算得到的弯折钢筋PBL剪力键的抗剪刚度为472.33 kN·mm-1，较直形钢筋PBL剪力键提升了10.67%。

3.5 应变分析

本文光栅应变传感器所测试的为传感器正下方60 mm范围内不同形态贯穿钢筋的应变。本次试验捕捉了整个加载过程中贯穿钢筋的应变值，图15给出了整个加载过程中两种贯穿钢筋的应变值。根据钢筋的应变变化可以得出贯穿钢筋是否屈服，进而分析PBL剪力键的破坏机理。由于试验的加载方向为千斤顶从混凝土底部向上施加位移荷载，为避免传感器受到混凝土或封装套的挤压，将光栅应变传感器布置在贯穿钢筋上表面，所测应变为压应变。

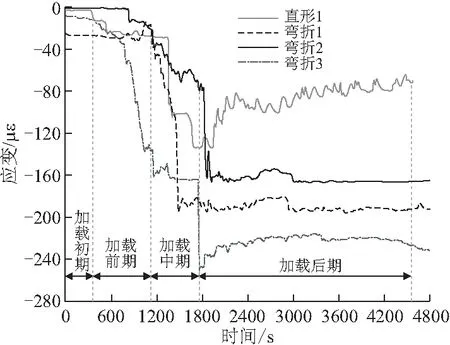
图15 贯穿钢筋应变随时间的变化趋势

由图15可见：

(1)整个加载过程可分为加载初期、前期、中期、后期四个阶段。在加载初期，钢-混结合面传递的剪力较小，主要由型钢与混凝土之间的粘结抵抗，两种贯穿钢筋的应变值很小，钢筋处于弹性阶段，将所测应变值换算成应力值，直形钢筋的应力为0.72 MPa左右，弯折钢筋的应力范围为0.81～4.88 MPa。

(2)结合面的粘结完全消除后试验进入加载前期，贯穿钢筋在荷载作用下开始受力，剪力由贯穿钢筋与环形混凝土榫共同抵抗，钢筋上表面开始压缩，传感器监测到的应变逐渐增大。

(3)试验进入加载中期后，直形钢筋的应变变化不大，而弯折钢筋的应变仍在继续增大，对比此阶段的荷载滑移-曲线，此时直形钢筋试件所受剪力为397.23 kN，为最大剪力的96.4%，弯折钢筋试件所受剪力约为最大剪力的91.2%，加载速率及时间均相同的条件下，弯折钢筋的应变远大于直形钢筋的应变，说明弯折钢筋分配到的剪力更大。

(4)试验进入加载后期时，两种贯穿钢筋的应变值均无明显变化，这是由于此时的混凝土已严重开裂，混凝土对贯穿钢筋失去了约束作用，试件仅靠混凝土的残余强度进行承载。

4 数值分析

4.1 数值建模

尺寸按推出试件设置，模型中所有构件均采用C3D8R单元；混凝土榫与开孔钢板、工字型钢与混凝土的接触面均采用面面接触，并设置0.5的摩擦系数；混凝土底部施加全约束，荷载自钢板顶部向下施加，加载方式为位移加载；钢材采用双折线理想弹塑性本构模型，混凝土采用丁发兴[22]提出的单轴受力损伤本构模型，模型网格如图16所示。

图16 模型网格示意

4.2 试验与数值计算结果对比分析

(1)抗剪承载力及荷载-滑移曲线

由图14可见：对于两种贯穿钢筋PBL剪力键荷载-滑移曲线，有限元计算值与试验值较为吻合，规律也相同，有限元计算的荷载-滑移曲线也分为上升和下降两个阶段。直形钢筋PBL剪力键抗剪承载力的实测平均值为211.07 kN，对应滑移量为0.96 mm，有限元计算值为214.14 kN，对应滑移量为0.97 mm，计算误差为1.4%。弯折钢筋PBL剪力键抗剪承载力的实测平均值为233.07 kN，对应滑移量为1.07 mm，有限元计算值为231.20 kN，对应滑移量为1.02 mm，计算误差为0.08%。

(2)贯穿钢筋的应力

两种贯穿钢筋的最大Mises应力云图如图17所示。

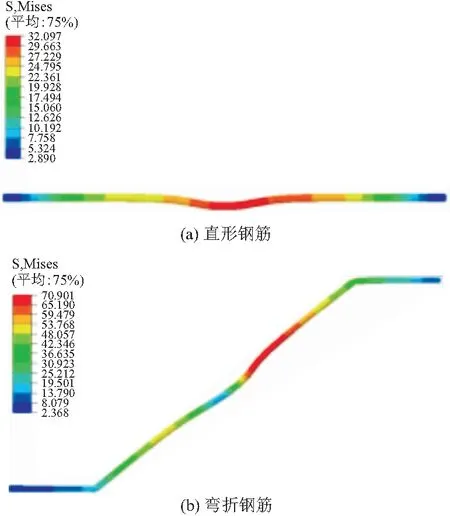
图17 两种贯穿钢筋应力对比/MPa

由图17可见：两种贯穿钢筋均在中部出现较高的应力水平，该部分位于开孔板中心，应力由钢筋中部向两端逐渐降低，钢筋端部的应力非常微小。直形钢筋的最大实测应力为29.78 MPa，有限元计算最大应力为32.09 MPa，弯折钢筋的最大实测应力为54.16 MPa，有限元计算最大应力为70.90 MPa，均发生在钢筋中部，有限元计算结果和推出试验相符。两种贯穿钢筋的最大应力均远小于钢筋的屈服应力371 MPa，说明PBL剪力键的破坏并非由贯穿钢筋屈服引起。

5 结 论

本文结合光纤光栅传感技术以推出试验的方式分析了普通直形钢筋PBL剪力键和弯折钢筋PBL剪力键的各项受力指标，得出以下结论：

(1)在各项材料相同的条件下，弯折钢筋PBL剪力键的承载力较普通直形钢筋PBL剪力键提高了10.42%，抗剪刚度提升了10.67%，经过改良后的PBL剪力键抗剪性能优于普通PBL剪力键；

(2)弯折钢筋PBL剪力键达到极限承载力后，结构不会立刻失效，承载力在下降阶段会出现二次上升，提高了PBL剪力键的延性；

(3)弯折钢筋PBL剪力键有效地改善了剪力连接件在达到承载力时混凝土出现贯通裂缝的现象，有利于结构的承载。

(4)PBL剪力键的破坏以纵向混凝土的开裂为主，使用PBL剪力键时应注意开孔板和贯穿钢筋的埋深问题。