基于有限元法改进螺栓连接刚度模型*

马雅丽，刘国超，危家勇，李灿灿，梁 晨

(大连理工大学机械工程学院，辽宁 大连 116024)

0 引言

螺栓连接性能的主要指标之一就是其刚度，它直接影响结构性能甚至于机器整机性能或精度，所以各国学者开展了大量研究。螺栓连接刚度主要由螺栓刚度和被连接件刚度两部分串联而成[1]。对于螺栓刚度而言，在德国、英国等各大标准中，均将螺栓等效为均质的圆柱进行刚度计算，计算方法已经基本达到统一。而国内外学者对被连接件刚度的研究主要从其受压层应力分布和受压层面积变化两方面入手。常用的方法有解析法、有限元法和实验法。CRC Press[2]在建立被连接件刚度求解的解析公式时，基于实验和有限元分析结果，提出了两点假设：被连接件的受压层应力沿其径向均匀分布；被连接件的受压层面积沿轴向呈空心圆柱体变化。在被连接件的受压层应力沿径向均匀分布的基础上，Fritsche G 等[3]提出受压层面积沿轴向呈空心圆锥体变化，并且求解了圆锥角为45°时的被连接件刚度。Budynas R G等[4]先后求解了圆锥角为45°和30°时的被连接件刚度，提出圆锥角为30°时被连接件刚度计算结果更为准确。德国工程师协会(VDI)通过实验建立了被连接件受压层面积变化的圆锥角的经验公式[5]。Juvinall R C等[6-7]对螺栓连接进行了有限元和实验分析，建立了被连接件受压层面积关于螺栓直径和被连接件厚度变化的经验公式。Motosh Nabil[8]通过有限元分析螺栓与被连接件接触区域内的节点位移求解了被连接件的刚度，并建立了其经验公式。 Wileman J[9]根据实验分析结果，提出了被连接件受压层应力并非均匀分布，而是近似满足于径向距离的4次关系式。Cao J[10]使用I-Scan压力分布系统测试被连接件受压层应力分布，得出被连接件受压层应力与螺栓的接触区域和非接触区域分布并不相同，在与螺栓接触区域内受压层应力满足径向距离的2次关系式，而只有在与螺栓的非接触区域，才满足径向距离的四次关系式。

目前大部分学者在研究预紧力作用下被连接件受压层应力和受压层面积变化时，多考虑被连接件厚度相同和材料属性相同的情况，实际上这两类参数都会影响被连接件受压层应力分布和受压层面积变化，从而影响刚度计算结果。基于有限元方法，研究了被连接件的弹性模量和厚度因素对被连接件刚度的影响，改进了螺栓连接刚度计算方法。

1 螺栓连接的有限元模型与分析

1.1 构建螺栓连接的有限元模型

为了更准确分析被连接件的弹性模量与厚度对被连接件刚度的以及螺栓连接刚度的影响，文中采用常规螺栓连接的有限元建模方法，构建了螺栓连接的有限元模型，如图1所示。

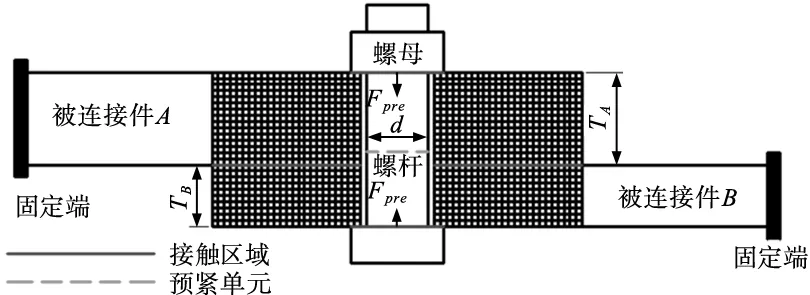
图1 螺栓连接有限元模型

模型分为被连接件A、被连接件B、螺杆和螺母4部分。将被连接件A左端和被连接件B右端全部固定，螺母与螺杆之间的旋合部分完全粘接，螺母与被连接件A之间、 被连接A与被连接件B之间、被连接件B与螺杆头之间建立有摩擦接触对，摩擦系数全部设定为0.3。在螺杆上建立预紧单元，施加预紧载荷8500 N。被连接件A、被连接件B、螺杆和螺母全部选用八节点的solid186单元，同时为了避免边缘效应，被连接件A和被连接件B接触区域的长度和宽度取为螺栓直径的9倍。螺杆和螺母的材料属性弹性模量设定为216 000 MPa和泊松比设定为0.3保持不变。

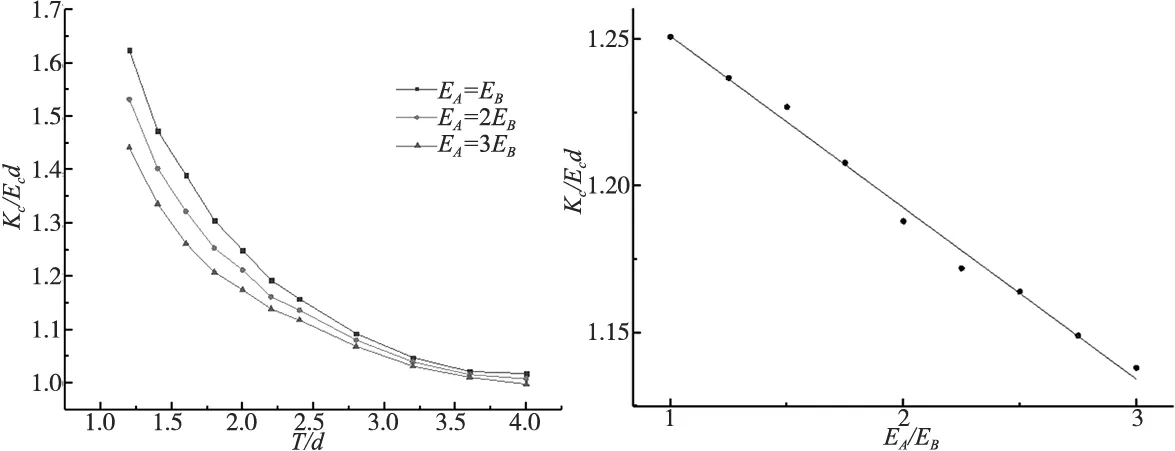
(a) 刚度随被连接件厚度与螺栓直径比变化 (b) 刚度随弹性模量比值变化

1.2 被连接件材料的弹性模量对其刚度的影响

采用常规的被连接件刚度的研究方法，将被连接的刚度、厚度和弹性模量转化为无量纲的量，分析被连接件刚度随被连接A、被连接B的弹性模量和厚度的变化规律，并建立其解析公式，如式(1)所示：

(1)

式中，Kc为被连接件刚度；EA和EB分别为被连接件A和被连接件B的材料弹性模量，Em为被连接件A和被连接件B的等效材料弹性模量，Em=EAEB/(EA+EB)[4-5]；TA和TB分别为被连接件A和被连接件B的厚度，T为被连接件总厚度，T=TA+TB；d为螺栓直径。

采用参数化分析方法分析刚度比Kc/Emd随被连接件材料弹性模量比EA/EB的变化规律。控制被连接件厚度比TA/TB不变。为了比较被连接件A和被连接件B的材料弹性模量不同对被连接件刚度的影响，将被连接件A和被连接件B的材料弹性模量分为三种组合方式：控制被连接件A和被连接件B的关系分别为EA=EB、EA=2EB和EA=3EB。被连接件厚度与螺栓直径比T/d变化范围从1.2～4，由于T/d<2.4时，被连接件刚度比变化幅度较大，而当T/d>2.4时，被连接件刚度比变化幅度较小，所以T/d的每次变动范围被非均匀化处理，T/d<2.4时，每次变动0.2，T/d>2.4时，每次变动0.4。三种被连接件材料弹性模量组合方式的刚度计算结果如表1所示。

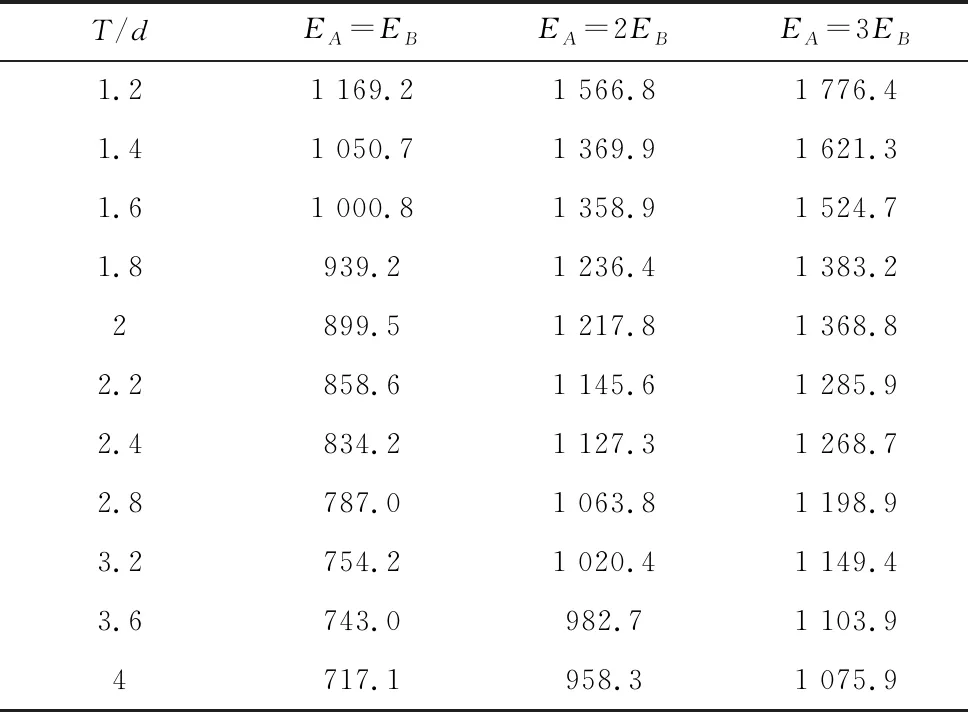
表1 材料影响下的被连接件刚度 (N/μm)

被连接件A和被连接件B的材料弹性模量不同会影响被连接件的刚度，无论T/d为何值，被连接件A和被连接件B的材料弹性模量比值越大，被连接件的刚度也就会越小。T/d越小，被连接件A和被连接件B的材料弹性模量不同对被连接件的刚度影响越大，当T/d=1.2时，组合3的被连接刚度相对于组合1下降了11.3%，当T/d=4时，组合3的被连接刚度相对于组合1下降了1.3%，如图2a所示。

进一步分析被连接件A和被连接件B的材料弹性模量比值对其刚度的影响。控制被连接件B的材料弹性模量和T/d=2不变。被连接件A的材料弹性模量以被连接件B的倍数均匀化增大，每次增大0.25倍。考虑到工程螺栓连接实际情况，被连接件A的材料弹性模量最大值为被连接件B的3倍取EA=3EB。被连接件的刚度随着被连接件A和被连接件B的材料弹性模量比值的变化规律如图2b所示。根据上述分析结果，拟合出刚度比与其两被连接件弹性模量之比的解析式：

Kc/Emd=-0.058EA/EB+1.309

(2)

1.3 被连接件厚度对其刚度的影响

采用参数化分析方法分析刚度比Kc/Emd随被连接件厚度比TA/TB的变化规律。控制被连接件厚度比EA/EB不变。为了比较被连接件A和被连接件B的厚度不同对被连接件刚度的影响，控制被连接件厚度T不变，将被连接件A和被连接件B的厚度分为三种组合方式：控制被连接件A和被连接件B的厚度的关系分别为TA=TB、TA=2TB和TA=3TB。被连接件厚度与螺栓直径比T/d变化范围从1.2～5.4，每次变动0.3。三种被连接件厚度组合方式下的刚度计算结果如表2所示。

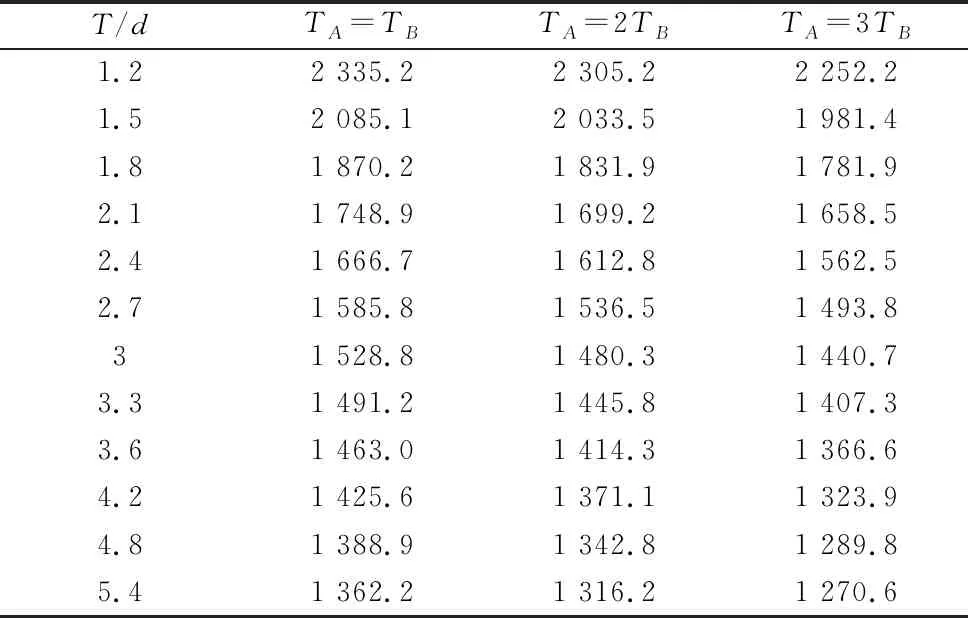
表2 厚度影响下的被连接件刚度(N/μm)

被连接件A和被连接件B的厚度不同会影响被连接件的刚度，无论T/d为何值，被连接件A和被连接件B的厚度比值越大，被连接件的刚度也就会越小。T/d越小，被连接件A和被连接件B的厚度不同对被连接件的刚度影响越小，当T/d=1.2时，组合3的被连接刚度相对于组合1下降了3.5%，当T/d=5.4时，组合3的被连接刚度相对于组合1下降了12.8%，如图3a所示。

(a) 刚度随被连接件厚度与螺栓直径比变化 (b) 刚度随厚度比值变化

进一步分析被连接件A和被连接件B的厚度比值对其刚度的影响。控制T/d=3.6不变。被连接件A的厚度以被连接件B的倍数均匀化增大，每次增加0.25倍。考虑到工程螺栓连接实际情况，被连接件A的厚度最大值为被连接件B的3倍取TA=4TB。被连接件的刚度随着被连接件A和被连接件B的厚度比值的变化规律如图3b所示。根据上述分析结果，拟合出刚度比与其两被连接件厚度之比的解析式：

Kc/Emd=-0.031EA/EB+1.047

(3)

2 螺栓连接刚度的解析模型

通过第1节螺栓连接有限元模型分析结果可知，被连接件材料的弹性模量和厚度对其刚度有影响，并且被连接件刚度与其材料的弹性模量比和厚度比近似满足工程线性关系。所以根据螺栓刚度的理论公式、被连接件刚度及其材料的弹性模量和厚度的关系建立螺栓连接的解析式。螺栓连接刚度由螺栓刚度和被连接件刚度两部分串联而成[1]：

(4)

式中，K为螺栓连接刚度；Kb为螺栓刚度；Kc为被连接件刚度。根据德国工程师协会(VDI)标准，螺栓刚度通常将螺栓等效为均质的圆柱进行求解[5]。

(5)

假设预紧力作用下的被连接件其受压层应力径向均匀分布，其受压层面积轴向圆锥体变化[2]。如图4所示。

图4 被连接件受压层面积的轴向变化

被连接件材料的弹性模量和厚度通过影响被连接件受压层面积来影响其刚度，而受压层面积的大小由圆锥角θm决定，联合所拟合式(2)、式(3)，建立圆锥角θm随被连接件材料的弹性模量和厚度变化的解析式：

(6)

被连接件的受压层面积

(7)

根据胡克定律应力应变关系，被连接件的刚度为：

(8)

联合式(4)～式(8)，螺栓连接的刚度为：

(9)

本节根据螺栓刚度的理论公式、被连接件刚度与其材料的弹性模量和厚度的关系建立螺栓连接的解析式。在相同的T/d的情况下，将通过式(9)的螺栓连接刚度计算结果与德国工程师协会(VDI)的实验结果对比，如图5所示。

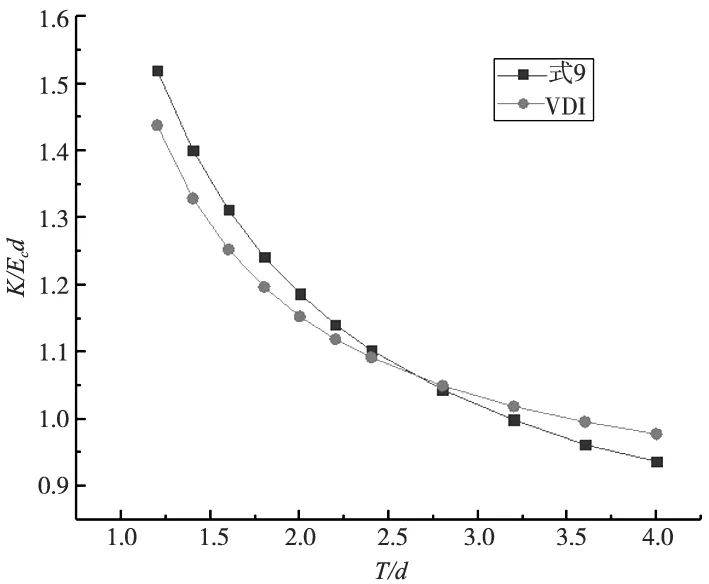
图5 螺栓连接刚度解析模型的对比验证

对比结果表明：式9的螺栓连接刚度计算结果与德国工程师协会(VDI)的实验结果误差小于8%，式9的螺栓连接刚度计算较为准确。

3 结论

本文建立了螺栓连接的有限元模型，通过有限元仿真研究了被连接件材料的弹性模量与厚度对螺栓连接刚度的影响。得出结论如下：

(1)被连接件之间的弹性模量比值会影响被连接件刚度，与被连接之间的弹性模量相同的情况相比，两者之间的比值越大，被连接件刚度也就会变得越小。刚度变小比例会受到螺栓直径和被连接件厚度的影响，T/d越小，被连接件刚度减小比例就会越大。

(2)被连接件之间的厚度比值会影响被连接件刚度，与被连接之间的厚度相同的情况相比，两者之间的比值越大，被连接件刚度也就会变得越小。刚度变小比例会受到螺栓直径和被连接件厚度的影响，T/d越大，被连接件刚度减小比例就会越小。

(3)根据被连接件材料的弹性模量和厚度对被连接件刚度的影响，建立了受压区域面积变化的公式，进而建立螺栓连接刚度的解析式。通过解析式的螺栓连接刚度计算结果与德国工程师协会(VDI)的实验结果对比，误差小于8%，螺栓连接刚度计算较为准确。