基于改进卷积神经网络轴承故障诊断*

庞 俊，刘 鑫，段敏霞，任海莉，侯鑫烨

(太原科技大学电子信息工程学院，太原 030024)

0 引言

现代机械设备正在朝复杂、高强度的工作条件下进行，一旦发生故障，那就可能是灾难性的，因此机械故障隐藏着巨大的风险和经济损失[1]。轴承是机械设备重要的零部件，为了使一些设备能够正常运行，轴承的诊断就是必不可少的[2]，据统计有30%是由轴承的损坏造成的[3]。现在机械设备故障数据海量化，机械设备检测迈入了“大数据”时代。

大数据时代是如何在海量的数据中自动进行特征挖掘，以取代人工进行特征提取，对轴承进行实时检测，保证故障诊断的准确性和高效性。因此处理工业“大数据”的智能诊断就慢慢发展起来，其中卷积神经网络故障诊断就受到广泛的关注[4]。轴承故障诊断是机械研究领域的一个重要方向，故障诊断主要分为两个步骤：一是特征提取，二是模式识别。传统的特征提取的方法可以分为时域分析、频域分析、时频域分析这三大类方法；模式识别的方法主要有支持向量机[5]、多层感知器[6]等。由于卷积神经网络在模式识别、图片分类等领域有良好的特征学习能力，将深度学习模型运用于轴承故障诊断中，成为近些年来国内外专家学者们研究的热点[3]。Janssens O等用卷积神经网络机械轴承故障诊断，比传统故障诊断准确率提高了6%[7]；Chen Lu等运用贪婪训练的逐层传递规则，对深层次结构进行鲁棒性训练[8];Hoang Duy tang等建立神经网络模型进行轴承故障诊断，把原始信号转换成图像作为输入，可以达到较高的精度和性能[9]。虽然CNN提高了故障诊断的准确率，但在数据预处理和网络结构上还存在一定的问题：①如果对输入数据进行快速傅里叶变换或者小波变换，会使得一些故障信号的时域特征丢失；②激活函数的运用会使模型出现梯度消失和均值偏移，影响模型对轴承故障诊断准确率。因此，本文提出了对激活函数线性修正单元进行改进，以解决梯度消失所带来的诊断准确率低的问题；卷积神经网络加入了两层残差神经元层加深网络；结合成一种新的故障诊断CNN模型，在与一些其它智能故障诊断相比较，显示出了更好的故障诊断优势。

1 卷积神经网络故障诊断

1.1 激活函数

激活函数就是将非线性的的特征映射到神经网络中的，如果不用激活函数，在网络中的每层输入都是上一层的线性输出，不管网络有多少层都是没有意义，这样只认为有一个隐藏层的作用，网络的训练能力就有限；如果使用，激活函数就会让网络中加入一些非线性因子，这样深层卷积神经网络的表达能力就更强。

1.1.1 修正线性单元

CNN中通常采用的激活函数为修正线性单元(The Rectified Linear Unit，ReLU)，它的一般形式为：

(1)

1.1.2 改进修正线性单元

ReLU函数解决sigmoid激活函数出现的梯度消失，但ReLU函数出现了均值偏移。在x<0时，由于x=0神经元是非激活状态，后续训练中网络无法学习，运行结果不收敛。PReLU函数是ReLU的改进，很好的解决了x<0上的均值偏移问题[10]。迭代次数的增多会出现不收敛，过拟合，导致训练结果失真，于是出现了变体ReLU阈值函数[11]。

虽然ReLU阈值函数解决了过拟合问题，仍然存在均值偏移问题，所以对ReLU阈值函数选取不同的阈值位置，测试对应的loss，如表1所示。

表1 在x<0处不同阈值与测试准确率的关系

根据表1的结果选择x=-1，如公式(2)，定义此函数为tReLU。

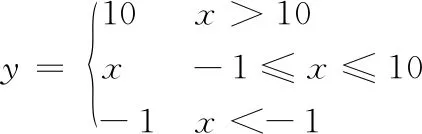
(2)

1.2 残差神经元

网络深度的增加，能更好的提取一些潜在，不容易被发掘的特征。已有研究证明，单纯增加网络深度，会在数据验证时出现准确率先升后降的现象，这就是所谓的退化问题[12]。加入残差神经会解决这些问题[13]，原理如图1所示。

如图1所示，x表示输入，F(x)表示第二层⨁前的输入，即公式(3)：

F(x)=W2f(W1x+b)+b

(3)

其中，W1、W2表示第一层和第二层的权重，f(·)表示ReLU激活函数，b表示偏置。

在图1中，设⨁之后激活函数之前的输出为H(x)，如果没有恒等映射，残差块就是一个普通的2层卷积网络，只将其优化成H(x)=x；但如果有恒等映射，则H(x)=F(x)+x，如果最优输出是x，则要把F(x)优化为0即可。

在CNN结构模型中为了减少计算量，运用1×1,3×3,1×1的卷积层[14]，两个1×1卷积分别负责通道上减少和增加维度，3×3卷积在它们之间提取特征。过程如图2所示。

图1 残差块的构成 图2 残差块结构图

1.3 卷积神经网络结构

在CNN中，用卷积和池化交替连接，引入残差神经元，最后用全连接，softmax分类，贯穿整个结构，其中激活函数运用tReLU。把此模型定义为RLCNN，结构如图3所示。

在提出的CNN模型中，先是把振动信号转换成二维振动图像[15],然后在4层交替的卷积池化中，加入残差同维神经元两层，最后两层全连接层分类。在RLCNN故障诊断中，基本的流程如图4所示。

图3 卷积神经网络结构图

图4 CNN故障诊断基本流程图

图3中，第1、2、5、6层的卷积核大小依次是5×5,3×3,3×3,3×3，个数依次是32,64,128,256，每层都运用最大池化层，其大小是2×2。第3、4层中运用残差神经元建立。

2 实验验证和性能分析

实验中应用凯斯西储大学和德国帕德尔伯恩大学轴承公开数据集对提出的RLCNN模型轴承故障诊断方法进行验证。其中RLCNN模型代码是通过Python3.5和TensorFlow进行编写，在Windows下的Pycharm2018 2.4下运行。

2.1 电机轴承故障诊断

2.1.1 数据集

图5 10种故障的振动图像

运用凯斯西储大学的轴承数据集[16]对提出的RLCNN模型进行验证。3种类型，有外圈故障(OF)、滚动体故障(RF)、内圈故障(IF)，每种类型有3种受损程度，受损直径0.18 mm、0.36 mm、0.54 mm，共9种故障类型，再加一种正常(NO)类型。这些数据是在4种负载条件(0 hp、1 hp、2 hp、3 hp)下记录的，在训练数据集中，每种负载有2000张振动图像；在测试数据集中，每种负载有400张振动图像，图像大小为64×64。它们的振动图像样品如图5所示。

从图5中可以看出，不同故障具有不同纹理，所以用图像特征的识别方式可以区分故障类型。

2.1.2 故障仿真结果

实验运行10组，每组经过50次的迭代，最后取10组的平均值为最终的识别准确率，则分类准确率与迭代次数的关系变化如图6所示。

图6 分类准确率和迭代次数的关系图

从图6中可以看出，从第1次迭代到第5次迭代故障识别准确率上升的快，到后面就慢慢平稳了，尤其是从40～50次迭代达到收敛，分类准确率达到了99.18%。图10为RLCNN第6组结果的混淆矩阵。

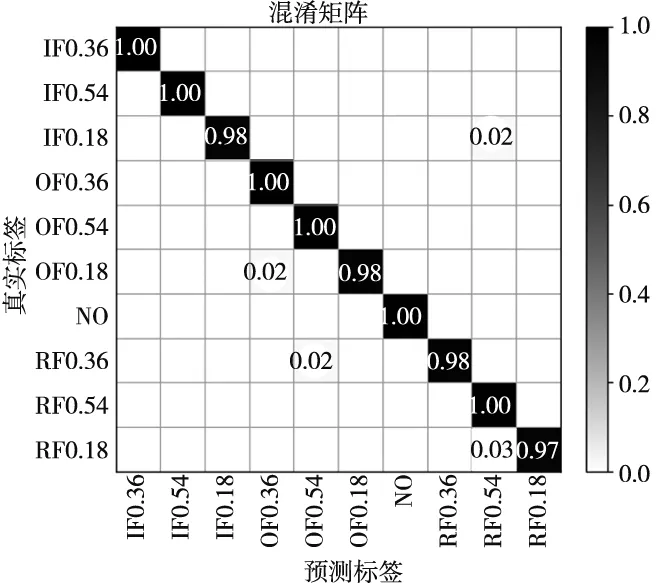
图7 RLCNN故障诊断的混淆矩阵

从图7可以看出，行表示预测标签，列表示实际的标签。结果显示，在IF0.36、IF0.54、OF0.36、OF0.54、NO、RF0.54的准确率均为100%，在RF0.18是最坏的，准确率为97%，在RF0.54错误分类最多为3%，2%的RF0.36、OF0.18分别被错误的分到OF0.54，OF0.36。IF0.36、IF0.54、NO的准确率为100%，没有其他条件被错误分类，显示着轴承故障完全识别。

为了评价提出卷积神经网络故障诊断模型的性能，将RLCNN模型与改进lenet-5的CNN[15]的故障诊断方法相比，其诊断准确率结果如表2所示。

表2 CNN模型与其他方法比较结果

从表2中可以看出，RLCNN模型的故障诊断准确率达到了99.18%，运行时间为4 h，改进lenet-5的CNN故障诊断的运行时间为5.8 h。虽然准确率不及改进lenet-5的CNN方法，但从时间差异上看出RLCNN模型在运算量上要少于改进lenet-5的CNN，模型运算效率有了较大提升。

2.2 机电传动系统轴承故障诊断

2.2.1 数据集

运用德国帕德尔伯恩大学提供的轴承数据集[17]对提出的RLCNN模型故障诊断方法进行分析。选中数据集中的一部分进行训练和测试，在数据集中有人为损伤和真实损伤(加速寿命的实验所产生)，在真实损伤中选中内圈的5种损伤，点蚀多重损伤1级(KI04)、点蚀单一损伤3级(KI16)、点蚀重复损伤1级(KI17)、点蚀单一损伤2级(KI18)、点蚀单一损伤1级(KI21)和正常(NO)共6种故障类型。每种类型共1200张振动图像，图像大小为128×128，分别从每种类型随机选择240张作为测试集，剩余为训练集。振动图像样品如图8所示。

图8 6种故障的振动图像

2.2.2 故障仿真结果

运行10组实验，每组迭代50次，对10组分类结果求平均值，故障分类准确率与迭代次数的关系如图9所示。

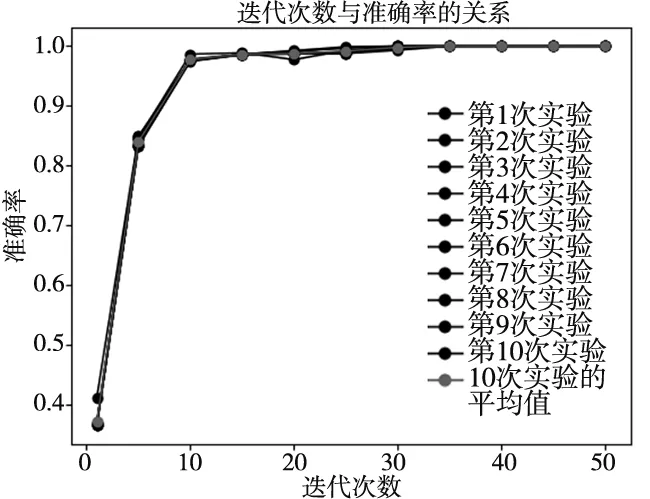
图9 故障分类准确率与迭代次数的关系图

从图9中所得，在第1次迭代到第30次迭代准确率都在变化，直到迭代30次后，故障分类准确率收敛，达到100%。为了更好地看清每种故障的分类准确率，绘制如图10为RLCNN模型故障诊断的混淆矩阵。

图10 RLCNN故障诊断的混淆矩阵

在图10中，每种故障的分类都是100%，从图中可以看出，KI04、KI16、KI17、KI18、KI21和NO没有其他错误分类，说明已被完全分离。

为了更好的体现RLCNN模型处理故障诊断的性能，此方法分别与JCNN[18]和STFT-CNN[19]中的卷积神经网络结构相比，其结果如表3所示。

表3 CNN模型与其他方法的比较结果

从表3可以看出，在处理大小为128×128振动图像，分6种故障，RLCNN模型诊断准确率达到100%，分别用JCNN、STFT-CNN对相同数据进行故障诊断，诊断准确率达到99.72%、94.03%，本文方法有了改进。

3 结论

基于一种改进的 ReLU 和残差神经元相结合新的CNN 网络模型可自动对振动图像进行特征学习，有效地实现对轴承故障诊断。相比于改进的 lenet-5 的 CNN 和JCNN，此方法更能提取出振动图像的深层次故障纹理特征，具有更好的分类能力。分别用凯斯西储大学和帕德尔伯恩大学的轴承故障数据对 RLCNN 模型进行测试，故障诊断准确率达到了 99.18%和 100%。