基于公差原则的装配体公差建模*

程彬彬

(桂林电子科技大学信息科技学院，广西 桂林 541004)

0 引言

公差分配是根据产品的功能要求、加工能力等，对尺寸公差、形位公差进行合理的确定与标注的过程。要进行产品的公差分配，必须先明确装配功能要求与各零件公差之间的关系，即装配体公差数学模型，装配体的公差数学模型是机械产品进行公差分配的基础，是CAD/CAE/CAM集成的关键。

目前对公差模型已进行了广泛的研究。1983年Requicha A A G[1]提出了漂移模型，用于描述公差域的边界信息；Hillyard R C等[2]提出了参数矢量化模型，这种模型对尺寸公差能够较好地处理；Bourdet P等[3]提出了小位移旋量模型(Small Displacement Torsor, SDT)，将几何特征要素在公差带内可能发生的变动用平动和转动两组旋量参数来表示；Walid Ghiea等[4]基于刚体运动学提出了雅可比旋量模型，可以同时表达尺寸公差和形位公差的工程语义，应用广泛；徐旭松等[5]研究了加工误差的累积模型；吴兆强[6]以SDT理论建立了公差变动累积模型，并进行了装配公差分析；王移风等[7]基于SDT理论研究了零件的公差建模方法，没有涉及装配体公差建模；唐哲敏等[8]利用齐次坐标变换，结合装配定位连接，建立了统计公差建模；许本胜等[9]基于特征的自由度变动进行公差的综合建模；程彬彬等[10-11]研究了零部件在实际工作载荷下的变形，对装配体公差模型进行了修正，进行了装配体公差优化分配。但目前的研究没有考虑公差原则(包括独立原则和相关要求)的影响，忽视了尺寸公差、形位公差之间的相互关系。而尺寸公差、形位公差在零件中是共同存在的，两者可以相对独立(独立原则)，也可以互相影响、互相补偿(相关要求，包括包容要求、最大实体要求、最小实体要求和可逆要求)，对产品的装配过程有着综合的影响。

针对上述问题，在现有装配体公差建模理论中引入公差原则，提出了一种基于公差原则的装配体公差建模方法，给出了工程实例应用，为后续进行公差优化设计奠定基础。

1 独立原则下装配体公差建模

独立原则是指在设计图样上尺寸公差、形位公差相互独立，互不影响，零部件的几何特征应分别满足要求的公差原则。目前的装配体公差建模大都以独立原则为前提[12]，研究零件的公差与装配功能要求之间的关系。其中，雅可比旋量模型算法简洁，能够清晰的表达尺寸公差和形位公差的变动和累积效应，在装配体公差建模领域应用比较广泛。雅可比旋量模型的表达式为[4]：

[FR]=[J][FE]

(1)

式中，[FR]、[FE]分别是装配功能要求、功能要素的旋量表示(SDT)，功能要素既包括零件本身的几何特征也包括零件之间的配合；[J]表示各组成环公差累积的雅可比矩阵。

(2)

式中，n代表装配尺寸链中组成环的个数，[J]FEi为各组成环对应的雅可比矩阵，其计算方法详见文献[4]，不再赘述。

2 相关要求下装配体公差建模

公差原则除了包含独立原则外，还包含相关要求。相关要求又分为包容要求、最大实体要求、最小实体要求和可逆要求[13]。

2.1 相关要求对功能要素旋量表示的影响

当设计图样采用相关要求时，图样上给定的尺寸公差Ta和形位公差ta就可以相互影响和补偿，从而对功能要素的SDT表示产生影响，所以必须对原来的雅可比旋量模型进行修正，才能正确表达功能要素的变动。下面以最大实体要求为例进行说明。

最大实体要求用最大实体实效边界对零件实际要素进行控制，当最大实体要求应用于被测要素时，应在形位公差框格中的公差值后面标注M，对实际轮廓的具体要求如下：

内表面(孔)Dfe≥Dmv=Dmin-ta且Dmin≤Da≤Dmax

(3)

外表面(轴)dfe≤dmv=dmin+ta且dmin≤da≤dmax

(4)

式中，Dfe、Dmv、Da、Dmax、Dmin分别是孔的体外作用尺寸、最大实体实效尺寸、局部实际尺寸、最大极限尺寸和最小极限尺寸，dfe、dmv、da、dmax、dmin分别是轴的体外作用尺寸、最大实体实效尺寸、局部实际尺寸、最大极限尺寸和最小极限尺寸。

根据式(3)、式(4)可知，当孔或轴的局部实际尺寸处处为最大实体尺寸时，功能要素的形位误差的最大允许值为图样上给定的公差值；当孔或轴的实际尺寸不再是最大实体尺寸时，功能要素的形位误差的最大允许值可以大于规定的公差值，且当孔或轴的局部实际尺寸处处为最小实体尺寸时，功能要素的形位误差可以达到最大值(尺寸公差与形位公差值之和)，即形位公差不是固定的，可以由图样上标注的尺寸公差进行补偿，局部实际尺寸Da或da与补偿后的形位公差t之间的关系(动态公差图)如图1所示。

图1 动态公差图

根据前面的论述，作用于功能要素的形位公差发生变化，必然导致其SDT的改变，需要将补偿后的形位公差t代替图样上标注的形位公差ta，根据图1补偿后的公差t呈线性变化，最大值为tmax=ta+Ta，当补偿后的形位公差取得最大值时对装配尺寸链的累积效应贡献最大。所以，在考虑最大实体要求对装配公差建模的影响时，取补偿后的形位公差的最大值tmax，以确保装配功能要求在所有情况下的满足。

2.2 相关要求下装配体公差建模的修正

由公式(2)可知，利用雅可比旋量进行装配体公差建模需要计算出反映公差累积效应的雅可比矩阵[J]以及几何要素的旋量表示[FE]。根据文献[4]，雅可比矩阵的计算仅与零件的基本尺寸相关，不涉及公差的相关计算，所以修正后的雅可比旋量模型只有[FE]发生改变。综上所述，相关要求下的装配体公差模型如式(5)所示。

(5)

式中，[FEi′]为相关要求下的旋量表示；u′、v′、w′、α′、β′、γ′为其对应的6个旋量参数。

3 工程实例

图2 机床尾座装配简图及组成零件图

3.1 雅可比矩阵的计算

图3是机床尾座装配过程的示意图。其中，顶尖与立柱的配合类型为过盈配合，底座与立柱的配合类型为平面配合，上述两处属于外部约束且都不存在间隙，根据SDT的理论可知对应的小位移旋量为零，即[FEi′|i′=2,4]为零，根据式(5)可知，上述两处的配合情况对装配体的功能要求[FR]是没有影响的，故对应的雅可比矩阵[Ji|i=2,4]也不需要计算。

图3 机床尾座装配过程

根据文献[4]计算雅可比矩阵的方法，机床尾座装配体各雅可比矩阵为：

(6)

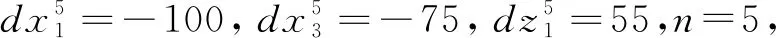
3.2 功能要素[FE]的计算

由图2可知，底座的平面上包含尺寸公差t1和平行度t2的公差要求，根据公差标注的要求，同一要素尺寸公差值要大于平行度的公差值，尺寸公差和平行度的公差带均为两平行平面组成，且尺寸公差的公差带方向和位置均是固定的，平行度的公差带仅方向是固定的，其位置浮动于位置度的公差带内。综上，在尺寸公差和平行度的综合作用下，底座上平面的平动不能超越尺寸公差t1的约束，且仅在Z方向上有限制，转动不能超越平行度t2的约束，在X、Y方向都有限制。根据平面的几何尺寸并结合式(5)[FEi′|i′=1]的表达式为：

(7)

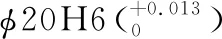
(8)

顶尖前端圆锥的轴线有同轴度的公差要求，同轴度的公差带是直径为公差值φt5的圆柱面内的区域，该圆柱面的轴线与基准轴线同轴。所以，同轴度公差对轴线在Y、Z轴即有平动的约束，也有转动的约束，根据图2中标注的尺寸，可以计算出顶尖前端圆锥的高度为25.98 mm。综上，[FEi′|i′=5]的表达式为：

(9)

将式(6)～式(9)代入式(5)就可得到机床尾座在公差原则(最大实体要求)下的装配公差模型，如式(10)所示：

(10)

4 结论

将公差原则引入装配体公差建模的研究中，提出了一种基于公差原则的装配体公差建模方法。结合机床尾座实例，利用上述方法介绍了装配体公差建模方法和步骤，验证了上述方法的有效性，扩大了装配体公差建模理论的应用场合，为下一步进行公差优化分配奠定了基础。