基于公差原则的装配公差统计分析*

王 辉，黄美发,2，郑素娟，杨盛宇，李超元

(1.桂林电子科技大学 机电工程学院，广西 桂林 541004；2.广西制造系统与先进制造技术重点实验室，广西 桂林 541004)

基于公差原则的装配公差统计分析*

王 辉1，黄美发1,2，郑素娟1，杨盛宇1，李超元1

(1.桂林电子科技大学 机电工程学院，广西 桂林 541004；2.广西制造系统与先进制造技术重点实验室，广西 桂林 541004)

为了提高机械产品的互换性，减少制造成本，公差原则在零件设计时有着广泛的应用，但是在现有的装配公差统计分析方法中却较少考虑零件的公差原则。为解决此问题，基于雅克比旋量理论建立了考虑公差原则的三维装配公差模型，并结合蒙特卡洛法对装配体进行统计公差分析，期间在用旋量区间表示特征变动时并考虑了旋量间的约束关系，使公差分析结果更加符合实际情况。最后以简易顶尖尾座装配体为实例，对比了零件应用不同公差原则时的公差分析结果，验证了所述方法的有效性。

公差原则；雅可比旋量模型；公差分析；蒙特卡洛

0 引言

与物理样机相比，数字样机可大幅度提高产品开发的速度和质量，而数字样机技术还存在着诸多的问题[1]。例如在对产品进行三维装配公差分析时不能很好的处理尺寸公差与形位公差的关系，即公差原则。而在实际几何产品设计中，为了更好满足产品的功能要求，其零件往往会有公差原则的要求，零件的公差原则要求会对最终的装配结果产生影响[2]。因此在三维装配公差分析中考虑公差原则对产品数字样机的制造有着重要的意义。

现阶段主要的三维装配公差分析模型有：利用欧式空间中的凸集描绘圆柱、平面、轴线等各种特征在公差限制下的特征变动范围的T-Map模型[3]；利用环路约束方程的一阶泰勒级数线性展开式代替非线性方程，并结合矩阵运算方法进行公差分析的矢量环模型[4]；以及在齐次坐标变换理论的基础上，Laperriere L 等提出利用雅可比矩阵结合SDT公差模型进公差分析的雅可比旋量公差模型[5]等。但是，目前的三维装配公差分析模型中却较少考虑公差原则[6]，故不能很好的对有公差原则要求的装配体进行公差分析。

本文在雅克比旋量模型的基础上，对有公差原则要求的装配体进行三维公差建模，并结合蒙特卡洛法对其进行公差统计分析，最后分析零件选用不同公差原则时对装配功能的影响。

1 雅克比旋量模型

雅可比旋量模型是一种结合雅可比矩阵与SDT理论的三维公差数学模型，主要用于装配体的公差分析[7]。雅可比旋量模型，采用雅可比矩阵表示各个特征FEi产生的变动对装配功能要求FR的影响关系，利用SDT模型表示各个FEi的公差。并在SDT模型中，结合区算法来表达各个旋量参数的变动范围[8]。雅可比旋量模型结合雅可比矩阵与SDT理论的优点，主要用于表达较为复杂的非线性装配关系。如式(1)所示，为雅可比旋量模型的表达式。

(1)

其中：

(2)

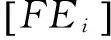
1.1 雅克比矩阵的构建

雅可比矩阵主要用于表达特征之间的误差传递关系，并利用矩阵乘积来表示特征间的误差累积[9]。在公差数学建模理论中，雅可比矩阵主要用于表示零件功能元素FE(FunctionalElements)，由于加工误差或装配误差产生的微小变动，对装配功能要求FR的影响关系，雅克比矩阵的表达式为：

(3)

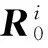
(4)

1.2 基于SDT理论的公差建模

以数学定义的公差模型是公差分析和公差综合的基础，在SDT公差模型中，将零件实际表面的误差认为是公称表面的一种微小的刚性变动，并用理想表面来代替实际零件表面[10]，如图1所示,其中,Oi-xiyizi表示特征所在的局部坐标系。SDT模型将实际表面看作是一理想的表面，而将实际表面产生的变动则看作是局部坐标系的变动。SDT模型主要用于研究特征表面在位置和方向上的变动。

图1 SDT原理

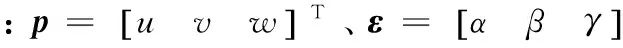
(5)式中：p表示控制位置旋量，ε表示控制方向旋量；u、v、w分别表示沿局部坐标系Xi、Yi、Zi轴的平动量；α、β、γ分别表示绕局部坐标系Xi、Yi、Zi轴的转动量。

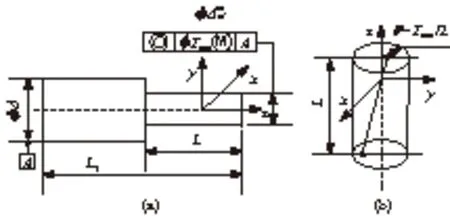
图2 最大实体要求应用于轴线同轴度公差

最终得到最大实体要求同轴度公差的数学模型为[6]：

(6)

式中：

(7)

其中,da表示实际尺寸，dmax、dmin分别为轴的最大和最小极限尺寸，式(6)、式(7)也就是旋量参数约束方程和旋量参数变动方程。

2 装配体公差统计分析

2.1 基于蒙特卡洛的公差分析

装配体公差分析是保证产品功能质量的重要途径，目前采用的公差分析方法主要包括：极值法、统计法、蒙特卡洛法等。相对于利用极值法进行的公差分析而言，统计公差分析法符合生产实际，节约生产成本。近年来，结合蒙特卡洛模拟法的装配体公差统计分析，已经得到了广泛的研究[12]。接下来本文将结合蒙特卡洛法，进一步研究装配体的公差统计分析。

本文基于式(1)所示的雅可比旋量模型，并结合蒙特卡洛模拟法，研究了装配体的公差统计分析。该方法利用雅可比旋量模型来表达零件误差(尺寸公差、位置公差)、装配误差在装配体中的累积，并根据已知的公差及其分布特性，采用蒙特卡洛法来模拟装配体关键特征(影响装配功能要求的特征)的变动以及零件的装配；最后根据模拟装配结果，分析FR的分布特性。

(8)

利用蒙特卡洛法，进行装配体公差统计分析的基本思想为：首先，利用蒙特卡洛法将关键特征的模拟问题，转化为根据特征旋量参数的分布规律及区间对参数进行随机取值的问题；再将得到的各个旋量参数的随机值，代入式(8)所示的公差分析模型中，计算FR的旋量参数值；最后重复该过程，得到一定数量的FR并对其进行统计分析，从而得到FR中各个参数所对应的公差分析结果。利用蒙特卡洛法进行装配体公差统计分析的基本流程，如图3所示。

图3 公差统计分析的流程图

基于蒙特卡洛法的装配体公差统计分析的具体步骤如下：

(1)求解旋量参数的分布规律及其区间

依据特征所指定的公差，确定各个旋量参数的变动范围及约束关系；并根据实际加工情况，确定特征各个旋量参数的分布规律。

(2)产生随机数模拟关键特征

根据特征各个旋量参数的分布规律及区间，随机生成各个旋量参数值模拟各个关键特征FEi，生成各个FEi的子样本。

(3)模拟关键特征的装配

将随机产生的各个关键特征FEi的子样本，代入式(8)中，进行关键特征的模拟装配，求出FR的单个子样本。

(4)FR的统计分析

不断循环步骤(2)、(3)，重复m次(模拟次数m越大则求解精度越高，但当m到达一定程度时，采用增大模拟次数的方法来提高模拟精度的效果并不显著)。求出FR的m个子样本，并对子样本进行统计分析，求出FR的平均值、极限值等。

2.2 装配体关键特征的旋量表示

雅可比旋量模型利用SDT模型中旋量区间内的随机取值来模拟装配体关键特征的变动，并运用雅可比矩阵来研究各个关键特征的模拟装配，以实现装配体的公差分析。所以说是利用雅可比旋量模型进行公差统计分析的基础。在实际生产过程中，由于加工条件、加工环境等综合因数的影响，使得各个特征的旋量参数呈现一定的分布规律[12]，但旋量参数的实际分布情况难以检测。因此，本文主要讨论，当各个旋量参数都服从正态分布，且相互独立的情况下的公差统计分析。

Ghie 等[11]提出的雅可比旋量模型的统计算法，在旋量变动模拟特征的过程中忽略了旋量之间的约束关系。本文把统计学中减少样本空间的思想引入到雅可比旋量模型的统计算法中，考虑了旋量之间的约束关系，使计算结果更加符合实际情况。本文将通过一个实例介绍该方法。

图4 顶尖零件图

用旋量表示图4所示零件上的特征(坐标系所在的圆柱)时， ①先把数据带入数学模型中(上文2.2小结已给出)，得到式(9)没有考虑旋量约束的参数变动区间和式(10)参数约束方程。②利用Matlab软件在旋量和尺寸公差区间内产生符合正态分布的n组随机数，并分别把这n组随机数分别带入到式(10)中。若满足式(10)，则保留这一组数值，若不满足，则剔除。③重复步骤②，若满足的组数为k，直到k/n≥99.73%(合格率应符合3δ原则[1])。④对满足条件的旋量数值进行统计，最后得到筛选数据后的旋量取值区间。不考虑旋量约束时的模拟特征合格率为98.22%，经过上述方法考虑旋量约束后的模拟特征合格率为99.93%，其最终得到旋量区间为式(11)所示。

(9)

(10)

式中，19.991≤da≤20。

(11)

3 实例验证

本文以简易顶尖尾座装配体为实例，进行装配体公差分析。如图5所示，该装配体由三个零件装配而成。其中，O0-xyz表示全局坐标系。顶尖尾座装配体对顶尖顶端沿Z方向的平动w，是产品的装配功能要求，要求装配体的FR0=±0.05mm(全局坐标系下Z方向的变动)。顶尖零件在公差原则选择上有三种设计方案，零件如图5a、图5b有最大、最小实体要求和图5c独立原则要求。下面利用上文所述方法，对零件应用不同公差原则时的装配体分别进行统计公差分析。该装配体公差值如表1所示。

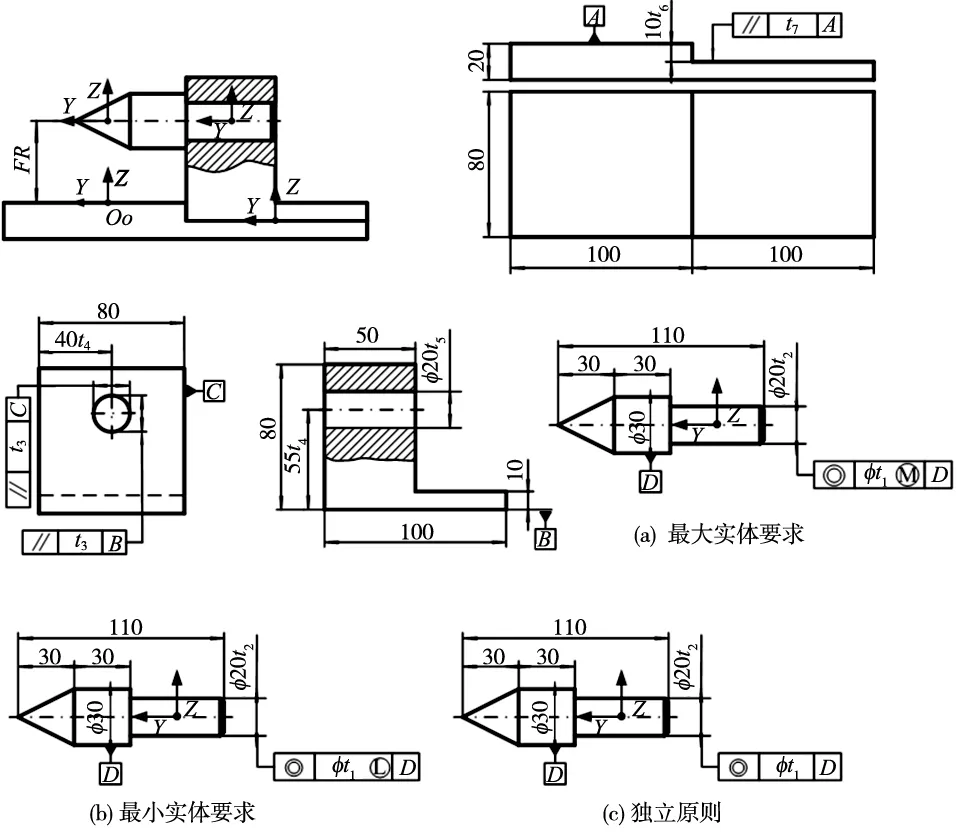
图5 顶尖尾座装配图

公差t1t2t3t4t5t6t7公差值0.01h5(0-0.009)0.01±0.01H6(+0.0130)±0.020.01

(12)

图6 机床尾座装配尺寸链传递图

然后利用本文2.3小节所提方法用旋量区间表示FE1,FE3,FE4,FE5这些关键特征，由于平面间的装配默认是完全贴合故小位移旋量为零，而孔轴配合时，只要不是过盈配合，就需要考虑配合的小位移旋量[12]。最后在旋量区间内按正态分布随机取值并带入到雅可比旋量模型中，取值次数N=2000。求得FR各个旋量参数的均值和方差后计算出置信水平为99.73%时参数的取值范围。

利用Matlab软件计算最终得到顶尖零件在不同公差原则时的装配体公差分析结果，如下表2所示。并建立了装配功能方向变动的分布图，如图7所示，图中横坐标表示FR(w)的变动值，纵坐表示公差分析结果落在某一区间的个数。

表2 不同公差原则时公差分析结果

图7 不同公差原则时FR变动分布图

结果表明，在这三种公差原则下的公差分析结果均小于装配功能要求FR0=±0.05mm，故需要适当扩大零件的公差值以达到节约成本的目的。当选择最大实体要求时，公差此时能扩到最大，故成本最低。

4 结论

本文在以数学定义的公差模型和三维尺寸链的基础上，建立了功能要求和功能要素之间的三维公差数学模型，然后用统计法对装配体进行公差分析，具体工作如下。

(1)建立了考虑公差原则的雅克比旋量模型，用旋量区间表示变动特征时，引入了统计学中减少样本空间的思想考虑了旋量之间的约束关系。

(2)采用蒙特卡洛法并结合雅克比旋量模型对装配体进行公差统计分析，并给出了具体步骤。

(3)最后利用顶尖尾座装配体为实例，验证方法的有效性，并对比了零件应用不同公差原则时的装配公差分析结果，为公差原则的选用提供了理论依据。

[1] 张为民,陈灿,李鹏忠,等. 基于雅可比旋量法的实际工况公差建模[J]. 计算机集成制造系统,2011,17(1):77-83.[2] 吕林森. 新编公差原则与几何精度设计[M]. 北京:国防工业出版社, 2007.

[3]JiangK,DavidsonJK,LiuJ,etal.Usingtolerancemapstovalidatemachiningtolerancesfortransferofcylindricaldatuminmanufacturingprocess[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2014,73(1-4): 465-478.

[4]HambletonJP,SloanSW.Aperturbationmethodforoptimizationofrigidblockmechanismsinthekinematicmethodoflimitanalysis[J].Computers&Geotechnics, 2013, 48(1):260-271.

[5]GuoJ,HongJ,WangY,etal.AnIdealMatingSurfaceMethodUsedforToleranceAnalysisofMechanicalSystemUnderLoading[J].ProcediaCirp, 2013, 10(12):306-311.

[6] 杨将新,茅健,曹衍龙. 基于MMR和LMR的同轴度数学模型[J]. 浙江大学学报(工学版),2007,41(12):1967-1970.[7]GhieW.ToleranceanalysisusingJacobian-torsormodel:statisticalanddeterministicapplications[M].INTECHOpenAccessPublisher, 2010.

[8]CaoYL,MathieuL,JiangJ.Keyresearchoncomputeraidedtolerancing[J].JournalofZhejiangUniversityenceA, 2015, 16(5):335-340.

[9] 孛朝旺. 基于新一代GPS和节点-基准链的三维公差分析方法研究[D]. 济南:山东大学, 2014.

[10]ChenH,JinS,LiZ,etal.Acomprehensivestudyofthreedimensionaltoleranceanalysismethods[J].Computer-AidedDesign, 2014, 53: 1-13.

[11]GhieW,LaperrièreL,DesrochersA.StatisticaltoleranceanalysisusingtheunifiedJacobian-Torsormodel[J].InternationalJournalofProductionResearch, 2010, 48(15): 4609-4630.

[12] 陈华，唐广辉,陈志强,等.基于雅可比旋量统计法的发动机三维公差分析[J].哈尔滨工程大学学报,2014,35(11):1397-1402.

(编辑 李秀敏)

Assembly Tolerance Statistical Analysis Based on Tolerancing Principle

WANG Hui1, HUANG Mei-fa1, 2, ZHENG Su-juan1, YANG Sheng-yu1，LI Chao-yuan1

(1.School of Mechanical and Electrical Engineering, Guilin University of Electronic Technology, Guilin 541004,China;2.Guangxi key Laboratory of Manufacturing System and Manufacturing Technology, Guilin 541004,China)

In order to improve the compatibility of mechanical products, reduce the manufacturing cost, tolerance principle can be applied in the component design, but in the existing statistical tolerance analysis method is less considered in tolerance principle of parts. In order to solve this problem, 3D assembly tolerance model is established considering tolerancing principle based on jacobian-torsor theory, and the statistical tolerance analysis was carried out on the assembly combined with the monte-carlo method, in the meantime, considering the constraint relationship between the screw when the screw interval is shown feature variations, make the tolerance analysis results more in line with the actual situation. Finally，a machine tailstock was taken as an example, compared the tolerance analysis results in different tolerance principle, and efficiency of the proposed method was verified.

tolerancing principle; jacobian-torsor model; tolerance analysis; monte-carlo

1001-2265(2017)05-0024-05

10.13462/j.cnki.mmtamt.2017.05.007

2016-08-31

国家自然科学基金资助项目(51365009)；广西制造系统与先进制造技术重点实验室主任课题(13-051-09-009Z)；桂林电子科技大学研究生教育创新计划资助项目(YJCXS201501)

王辉(1990—)，男，山东聊城人，桂林电子科技大学硕士研究生，研究方向为计算机辅助公差设计，(E-mail)409057149@qq.com；黄美发(1962—)，男，广西蒙山人，桂林电子科技大学教授，博士，博士生导师，研究方向为机电系统精度设计和智能测量方法。

TH162;TG506

A