多目标差分进化算法在轴系全息动平衡中的应用*

周建平，冷洪坤，温广瑞，冉祥锋，姜 宏

(1.新疆大学 机械工程学院，乌鲁木齐 830047；2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

多目标差分进化算法在轴系全息动平衡中的应用*

周建平1，冷洪坤1，温广瑞2，冉祥锋1，姜 宏1

(1.新疆大学 机械工程学院，乌鲁木齐 830047；2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

传统全息动平衡方法对转子进行动平衡时，仅以残余振动平方和作为标准对平衡效果进行评价，平衡效果受到平衡面和平衡精度及效率的约束。文章利用不同维度的标准benchmark测试函数验证了差分进化算法的优越性，研究了差分进化算法配重优化的原理，融合模拟退火因子提高算法的寻优能力，利用该算法对轴系进行全息动平衡优化，综合残余振动平方和、残余振动极值及残余振动均值等多个目标建立评价函数对轴系动平衡状况进行评价，通过实验验证了该方法的轴系动平衡效果良好。

评价函数；差分进化；平衡优化

0 引言

透平机械中轴系不平衡使附加载荷增大，是设备和零部件损坏的最常见的四大故障之一。振动作为不平衡的主要表现形式，不仅产生噪音加速轴承磨损、缩短机械寿命，严重时会造成破坏性事故[1]。现场动平衡的常用方法有影响系数法、振型平衡法和全息动平衡法[2-3]。影响系数法启停车次数较多，平衡面选择不当易出现病态矩阵，导致平衡量不合理，且对高阶振型灵敏度很低。振型平衡法需要预知转子系统的振型，必须在临界转速附近进行测量、振型做正交分解或仿真计算，对操作者要求较高，不宜实现计算机辅助。全息动平衡法利用全息谱技术集成测点、截面和整个轴系的信息，可以在任意转速下将失衡响应分解为力和力偶两部分并分别加以平衡，有效避免了以上两种传统平衡方法的不足，但受制于平衡面和平衡精度，使得传统求解所得配重的平衡效果不能保证最优。把转子动平衡视为一线性问题，将智能优化算法与全息动平衡相融合，可以有效提高平衡精度。

目前平衡效果评估多以单目标(残余振动平方和最小)为主，难以保证残余振动均匀性[4-5]。本文以残余振动平方和最小、残余振动均方差最小以及残余振动极差值最小三个方面为约束目标严格控制残余振动的大小，基于融合模拟退火因子的差分进化算法研究解决全息轴系现场动平衡多目标优化问题。

1 优化算法选择

Differential Evolution(DE)算法用于解决连续变量的全局优化问题[6]。工作步骤与遗传算法等其他进化算法基本相同，主要包括变异(Mutation)、交叉(Crossover)、选择(Selection)三种操作。基于种群的全局搜索策略，DE采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性。同时，DE可以动态跟踪当前的搜索情况，以调整其搜索策略，具有较强的全局收敛能力和鲁棒性。图1所示为标准差分进化算法的流程。

图1 标准差分进化算法流程

一个良好的算法应满足：初始阶段应有较强的全局搜索能力，以尽可能发现较多的全局最优解；后期阶段应具有较强的局部搜索能力，这样可以提高算法的求解精度和收敛速度。模拟退火算法通过赋予搜索过程一种时变(退火因子)且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。差分进化算法基于全局搜索策略，可以融合模拟退火因子来提高算法的计算性能[7]。

为验证差分进化算法的计算收敛性能，此处选取几个典型的benchmark测试函数分别利用不同优化算法进行求解，根据求解情况，对比各函数的优化效果。这几种算法分别为融合模拟退火因子的差分进化算法、带压缩因子粒子群算法、综合学习策略粒子群算法、序列前向选择算法。

(1)单峰函数

(1)

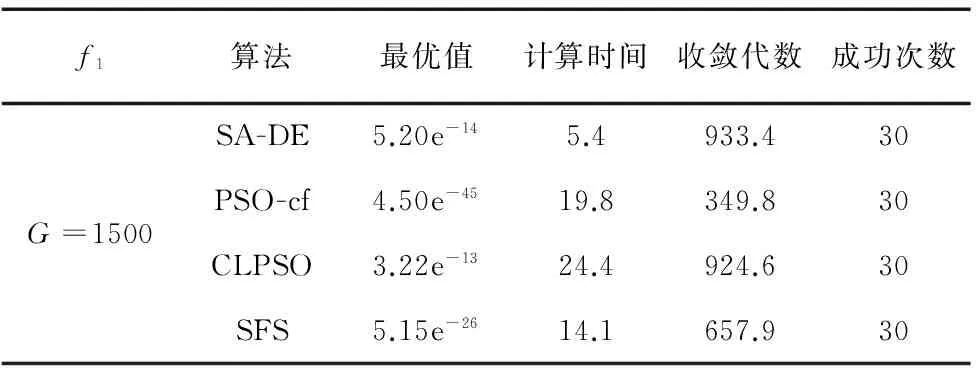
表1 单峰函数优化对比

(2)多局部极小值多峰函数

(2)

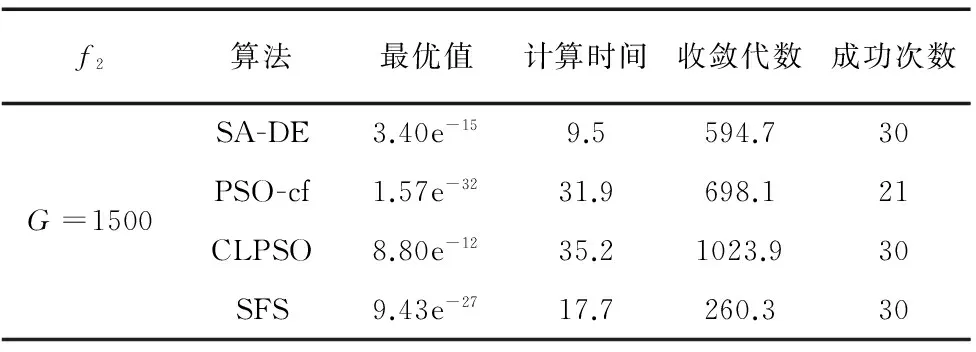
表2 多局部极小值多峰函数优化对比

(3)多局部极小值低维多峰函数

(3)

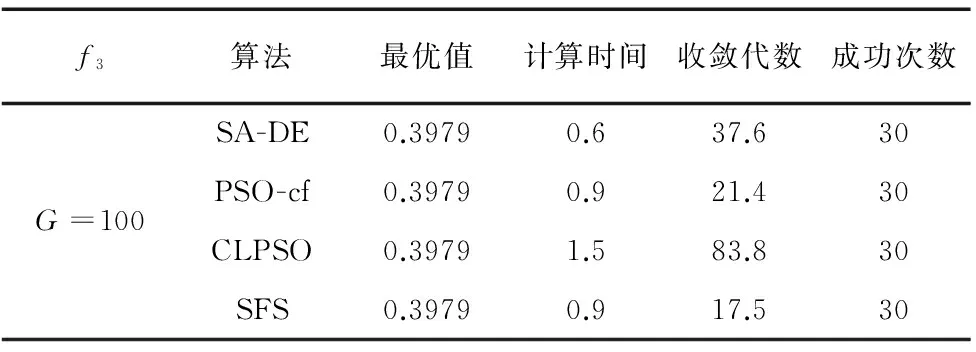
表3 多局部极小值低微多峰函数优化对比

由以上三个典型的函数模型求解情况可知，差分进化算法适用于不同测试函数且求解过程耗时最少，相比于其它几种智能算法具有较好的计算性能。

2 全息轴系动平衡

传统柔性转子动平衡的振动信息都是单个传感器从转子单向采集，忽略了转子系统各向刚度的差异性，必然给平衡带来误差，降低平衡精度。本文基于将幅、频、相信息高度综合的全息轴系动平衡方法研究多目标平衡优化。全息轴系动平衡采用三维全息谱表示机组的振动，使轴系振型和加重响应直观化[8]，通过试重获得的迁移矩阵具有良好的稳定性和可靠性，有利于提高平衡精度。在轴系某个加重面上添加1000g∠0°配重时在其它测重面上引起的振动响应矩阵即为迁移矩阵。根据迁移矩阵调整轴系的配重大小和相位，可显著减轻轴系不平衡。

设轴系具有M个平衡面、N个测振面，添加配重后轴系的迁移矩阵为：

(4)

不同配重下的转化算子为：

(5)

添加mg∠α°后机组的振动响应为：

(6)

配重后的残余振动方程为：

V0+AW1×C1+AW2×C2+…+AWi×

Ci+…+AWM×CM=V1

(7)

为消除轴系振动，为轴系添加一组合适的配重向量pij，平衡后的轴系振动方程应满足：

(8)

其中，Ai0为测振面i的原始振动；qi j为配重面j对测振面i的影响系数；pi为平面j上所加配重。一般情况下，轴系中配重面与测振面的个数并不相同，配重面数小于测振面数，现场动平衡完全消除各测振面的振动是不现实的。不同的配重对应不同的迁移矩阵，得到的残余振动也不尽相同，利用智能优化算法对确定的平衡配重进行优化可以得到最优的轴系配重方案。

3 差分进化配重优化

3.1 平衡优化目标

传统轴系现场动平衡以残余振动平方和最小为目标求得轴系配重方案，不能保证该配重方案下各测振面的振动均得到很好的消除，即有的测振面可能存在较大的振动。针对这种情况，可以引入转子振动的最大值和极差作为评价目标来评判平衡效果，该多目标优化配重方案的平衡效果可以达到最优[5]。

(9)

该下降半梯形模糊分布函数中：Mj为Fj(X)的最大值；mj是Fj(X)最小值。可知，当解愈接近函数最小值(最优解)时，其隶属度愈高。

利用线性加权法并给各目标函数分配不同的权重系数，得到各目标函数的平衡优化函数：

H(X)=λ1μ(F1(X))+λ2μ(F2(X))+λ3μ(F3(X))

(10)

其中，λ1、λ2、λ3为线性加权中各隶属度函数不同的权重系数，此处仍然选取残余振动平方和最小为主要目标评判平衡标准，残余振动的极值和极差为辅助目标，根据文献可知在选取λ1=0.7，λ2=0.2，λ3=0.1时所得配重方案可以取得较优的平衡效果。

3.2 差分进化配重优化

差分进化算法的目标向量设为xi=(x0,i,…,xN-1,i)T，试验向量设为vi=(v0,i,…,vN-1,i)，其中i=0,1,…,NP-1 ，N是目标函数的维数，一般常用的变异算子有五种，此处列举两种：

(11)

其中，G为迭代次数，r1,r2,r3∈(0,NP-1)为取值范围内各不相等的整数，F为变异因子。

ui=(u0,i,…,uN-1,i)T

(12)

利用上述公式可以增加参数向量的多样性，其中CR为交叉概率。根据相关文献取CR=0.1,F=0.5。

为保证算法前期能具有较高的全局搜索能力以便得到较多的合适解，在后期能提高局部搜索能力加快收敛速度，文章引入模拟退火策略：

(13)

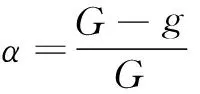
设轴系有K个配重面，差分进化算法的算法流程如下：

(2)根据转子振动信号求得转子的原始振动及迁移矩阵，计算转子平衡配重质量。根据所得转子平衡配重及轴系允许的配重阈值确定个体搜索的区间。

(3)初始化差分进化种群，确定多目标下各子目标函数的最大值和最小值。

(4) 根据原始振动、迁移矩阵和个体所对应的配重计算出转子残余振动。

(5)根据多目标适应度函数H(X)=λ1μ(F1(X))+λ2μ(F2(X))+λ3μ(F3(X))，计算出种群个体的适应度。

(6)按照差分策略调整个体的交叉和变异，得到新的个体。

(7)返回第(4)步进行迭代，求得最佳配重质量与角度。

4 轴系动平衡差分进化优化算法的验证

某电厂2号汽轮机发电机组进行修整，对转子进行动平衡，汽轮机组的结构和传感器安装如图所示。电厂试图通过动平衡降低高中压转子的振动。

图2 汽轮机发电机组结构示意图

平衡过程中，选择1#轴承端面法兰、2#/3#轴承和4#/5#轴承间联轴器凸缘作为平衡面，即图中所示平衡面A、B、C。通过人工对机组进行现场动平衡，根据优化配重方案，可明显改善高中压转子振动。

平衡机组中各配重面的迁移矩阵可以根据机组的历史平衡数据计算得出，也可以利用现场动平衡过程中的配重和轴振信号计算得出，利用融入模拟退火因子的差分进化算法计算机组轴系的动平衡配重并对其进行优化。表4所示为多目标差分进化算法优化后得到的机组转子现场动平衡配重方案。经配重平衡后的机组转子振动及平衡前的振动对比如表5所示，可以看出，经多目标平衡优化后的机组高中压缸的振动明显改善，各轴瓦的振动也相对一致，满足电厂对机组轴振控制的要求。

表4 差分进化计算出的平衡配重方案

表5 机组现场动平衡前后及优化后轴振对比

表6 优化后的轴振情况

5 结论

差分进化算法与其它智能算法相比，具有计算量小、收敛速度快的特点。文章将融合模拟退火因子的差分进化算法应用在石化机组现场动平衡中，以多个目标为约束对转子动平衡效果进行评价，满足机组现场动平衡的实际要求，可以解决轴系动平衡的多目标优化。

[1] 刘春英. 理论浅析回转件转子动平衡[J].科技与企业，2015(22):198-200.

[2] 康成亮. 用于电动工具转子的全自动平衡机的影响系数标定方法研究[J].组合机床与自动化技术，2007(6):23-25.

[3] 刘石,屈梁生. 全息谱技术在轴系现场动平衡方法中的应用[J]．热能动力工程，2009,24(1)：24-30.

[4] 瞿红春,崔秀峰. 基于遗传算法的动平衡优化研究[J]．中国民航大学学报，2013,31(5):24-26.

[5] 张西宁,赵明,温广瑞. 一种轴系全息动平衡配重的多目标优化方法[J]．中国机械工程，2010，21(16)：1974-1977.

[6] 张春美. 差分进化算法理论与应用[M].北京：北京理工大学出版社，2014.

[7] 杨艳霞. 一种基于模拟退火操作的混合差分进化算法[J].智能系统学报，2014，9(1)：109-114.

[8] 屈梁生. 机械故障的全息谱诊断原理[M].北京：科学出版社，2007.

(编辑 李秀敏)

Multi-objective Differential Evolution Algorithm in Holo-balancing

ZHOU Jian-ping1，LENG Hong-kun1，WEN Guang-rui2，RAN Xiang-feng1，JIANG Hong1

(1.College of Mechanical Engineering,Xinjiang University ,Urumqi 830047, China; 2.State Key Laboratory of Mechanical Manufacture System Engineering, Xi′an Jiao Tong University，Xi′an 710049, China)

when the conventional holo-balancing method balances the rotors, only using the sum of residual vibration square as the standard to evaluate the effect of balancing which the effect is limited to the balancing area and accuracy. To solve the problem above, this paper uses different dimensions of standard benchmark test functions to verify the superiority of the differential evolution algorithm，and research on the principle of differential evolution algorithm to optimize counterweight, fusion simulated annealing algorithm factors to increase optimization capacity. Using this algorithm to optimize holographic fields balancing and integrating the maximum ,uniformity and sum of square of residual vibration residual vibration squares and residual vibration to establish evaluation function to evaluate the status of the fields balancing with multiple targets. The effectiveness of the proposed method is verified by a practical balancing application.

evaluation function;differential evolution;balancing optimization

1001-2265(2017)05-0017-04

10.13462/j.cnki.mmtamt.2017.05.005

2016-07-28；

2016-09-06

新疆维吾尔自治区科技支疆项目(项目201404071245)

周建平(1974—)，男，江苏赣榆人，新疆大学教授，博士，研究方向为特种加工与数控技术、信号采集与分析，(E-mail)rxf_9106@163.com。

TH124；TG659

A