基于群组层次分析法的加工中心采购方案决策*

秦志远，黄海松，张 慧

(贵州大学 现代制造技术教育部重点实验室，贵阳 550025)

基于群组层次分析法的加工中心采购方案决策*

秦志远，黄海松，张 慧

(贵州大学 现代制造技术教育部重点实验室，贵阳 550025)

加工中心是制造行业的关键装备，对其采购方案进行决策需要综合考虑多方面影响因素。为使决策结果更加客观可行，将群组层次分析法与模糊评价法相结合，从精度指标、坐标轴、刀库、运动性能、成本五个方面进行分析。首先在yaahp软件中建立评价体系得到指标权重，然后建立模糊评价矩阵确定指标隶属度及指标分值，其次根据方案得分确定最优方案，最后通过一个实例验证了该方法的可行性。

加工中心；群组层次分析法；模糊评价

0 引言

加工中心是一种高度机电一体化的先进制造装备，相比传统数控机床，一次装夹即可实现多道加工工序，其具有的快速自动换刀与高效高质复杂型面加工等优势使其成为制造业中的关键装备[1]。因为精度、工艺和效率等问题，国内使用的高端加工中心多为国外进口[2]。近几年来，随着自主技术的发展，国内能生产加工中心的厂家正在不断增加，如沈阳机床厂的GMC2590u桥式五轴联动加工中心，大连机床厂的VDM500五轴立式加工中心和济南机床二厂生产的XV2525×60高架式五轴联动加工中心等，上述加工中心均能实现一次装夹完成零件的钻、铰、镗、铣、攻丝等多道工序。加工中心品种增多，而评判其性能优劣的过程难以量化，因此有必要建立一套加工中心性能评价与选购体系。

决策是人们根据已掌握的信息对解决问题的方案进行抉择的过程。决策过程既要有科学的定量分析，也要强调定性分析的重要性[3]。在工程领域，常用的评价与决策方法包括模糊综合评判法[4]、灰色系统理论[5]、TOPSIS法[6]、灰色关联度分析法[7]等。模糊综合评判法将定性指标量化，体现定性与定量的结合；灰色理论充分考虑人的判断模糊性；topsis法通过计算备选方案与正理想解和负理想解的距离选择最佳方案。但单一方法普遍存在太过偏重主观判断或专家意见，或是各指标分配相同权重的问题，而这显然是不符合常理的，也不能满足工程要求。

群组层次分析法(Group analytic hierarchy process, GAHP)由层次分析法(AHP)发展而来，它不仅将定性判断与定量分析相结合，而且集合多位专家的判断信息，并根据专家的经验和知识对不同专家的判断信息设定权重，有效避免主观差异性，使决策结果更加合理。模糊评价是通过问卷调查、访谈调查及观察调查等方法征集意见，对低级指标划分等级，确定该指标的等级隶属度[8]。本文将群组决策分析法与模糊评价进行有效结合，实现对加工中心的模糊评价与采购方案的决策。

1 基于层次分析法的评价体系构建

在满足使用需求的前提下，可供选择的加工中心种类有很多种。但各类加工中心在加工精度、刀库容量、成本消耗等方面各有利弊。评价体系一般划分为目标层、指标层和方案层。综合考虑影响加工中心采购方案决策的多种因素，最终选择精度、坐标轴性能、刀库性能、运动性能[9]、成本五个因素为一级指标，定位精度、可控轴数、刀库容量、主轴转速等15个因素为二级指标建立如图1所示的加工中心模糊评价与采购方案决策体系。

图1 加工中心模糊评价与采购方案决策体系

精度指标B1包括：定位精度C11，数控机床工作台等移动部件在确定的终点所达到的实际位置的水平；重复定位精度C12，应用相同程序加工一批零件的连续质量的一致度；分度精度C13，分度工作台进行分度操作时，理论回转角和实际回转角的差值；脉冲当量C14，执行运动部件的移动量。

坐标轴性能指标B2包括：可控轴数C21，机床数控装置能控制的坐标数目；联动轴数C22，机床数控装置控制的坐标轴同时到达空间某一点的坐标数目。

刀库性能指标B3包括：刀库容量C31，刀库容纳刀具的数量；换刀时间C32，将主轴用刀与刀库中下一工序用刀交换所需的时间。

运动性能指标B4包括：主轴转速C41,机床主轴的转动速度；进给速度C42，机床进给线速度;行程C43，坐标轴空间运动范围；摆角范围C44，机床摆角坐标的转角大小。

成本指标B5包括：价格C51，加工中心售价；可靠性C52，加工中心的使用可靠性，即故障率大小；维修成本C53，出现故障后所需维修费用及日常的维护费用。

2 评价指标权重的确定

群组层次分析法是在层次分析法的基础上综合多位专家的评判信息，首先计算单个专家的评判信息确定的指标权重，最后通过算术平均法或几何平均法对每个专家确定的指标权重进行合成，实现群决策。流程如图2所示。

图2 确定评价指标权重流程图

2.1 构造判断矩阵

层次分析法的基础信息是专家对每一层次中各要素进行两两比较判断相对重要性，为使其得到定量表述，常用1～9标度法，具体形式及含义如表1所示。

表1 1～9标度法及其含义

以总目标A为准则判断一级指标Bi、Bj的相对重要性为例，可得到判断矩阵简要形式如下：

A(A-B)=(aij)n×n

(1)

其中aij是元素Bi和Bj相对于准则A的相对重要性之比。判断矩阵具有以下性质：

(1)aij>0; (2)aii=1;

(3)aij=1/aji(i,j=1,2,…,n)

2.2 层次单排序

层次单排序是对某一确定层次内的所有要素根据重要性进行排序，此处元素重要性通过权重表示，该层次内所有元素的权重构成权重向量，权重向量的计算过程如下:

(1)求判断矩阵各行元素的几何平均值：

(2)

(2)将bi归一化，即可求得该判断矩阵所对应的权重向量：

(3)

可求得该层次元素对应的权重向量为：

W=(w1,w2,…,wn)T

2.3 一致性检验

一致性是指A比B重要，B比C重要，理论上A应当比C重要。理想的判断矩阵应当符合一致性，但实际应用中经常出现不符合一致性的情况，所以要进行一致性检验，必要时对判断矩阵进行调整。特别地，在群组层次分析法中要求每个专家的判断矩阵均要通过一致性检验。

进行一致性检验的公式如下：

AW=λmaxW

(4)

(5)

(6)

其中,A为判断矩阵，λmax为判断矩阵的最大特征值，C.I.为一致性指标值，R.I.为平均随机一致性指标值，可查询文献[4]，用于修正C.I.。当C.R.小于0.1时，认为判断矩阵符合一致性，否则需对判断矩阵进行调整后再次进行一致性检验。

2.4 层次总排序

层次总排序是指相对总目标某层次各指标要素重要程度的次序排列[10]，即计算方案层各方案相对总目标的重要性系数。总排序系数是自上而下将单层重要性系数进行合成。

假设共有k个层次，其中目标层为第1层，则方案层的排序向量为：

W=W(k)W(k-1)…W(2)

(7)

2.5 专家群决策

首先根据s个专家的学术水平、阅历、经验等确定每个专家评判信息的权重，然后综合专家确定的判断矩阵所对应的排序向量得到综合排序向量。加权算术平均综合向量法采用各个专家层次总排序向量的算术平均作为综合总排序向量WZ。

Wz=λ1W1+λ2W2+…+λsWs

(8)

3 方案指标分值的确定

为使结果具有较强的客观性，通过问卷调查、访谈调查等方法征集意见，然后结合征求意见结果和评价等级标度值确定方案指标分值[11]。

3.1 确定评价等级隶属度

首先确定评价指标集U，单个评价指标为ui；然后确定评价等级集V，划分5个评价等级分别为v1,v2,v3,v4,v5。

针对评价指标ui做出vk等级评定的人数为Nik，参与等级评定的人数为N，则可计算指标等级隶属度为：

(9)

则评价指标对应的隶属度函数为：

Mi=(mi1,mi2,mi3,mi4,mi5)

(10)

评价指标集内各个指标的隶属度函数组成隶属度矩阵：

(11)

3.2 确定评价等级标度值

为使结果具有较强区分度且便于比较，确定好，较好，中等，较差，差五个指标评价等级[12]，对应的标度值：X=(100,80,60,40,20)。

3.3 方案分值确定

根据不同方案指标权重、评价等级隶属度及评价等级标度值得出各方案分值Y，进行排序后可选择最佳方案。

(12)

4 实例应用

某实验室欲采购一台加工中心用于科研和教学，现有四种加工中心基本符合要求。综合考虑使用需求、设备性能和科研经费等问题，运用群组层次分析法对备选方案进行进一步的优化选择。

4.1 指标权重确定

yaahp分析软件可以方便的建立评价体系的层次关系并可以简单方便的计算指标权重[13]。yaahp建立判断矩阵的同时进行一致性检验[14]，如不能通过一次性检验能够自行对判断矩阵进行调整。新版本加入了群组决策分析模块，故选择该软件计算指标权重。

在该案例中，依据专家学术水平、经验、阅历以及对该行业了解程度确定参与决策的四位专家所占权重分别为0.3，0.3，0.2，0.2。图3为yaahp群决策分析模块，图4为yaahp中专家1的分析结果，最终指标权重分析结果见表2。

图3 yaahp群决策模块

图4 专家1分析结果

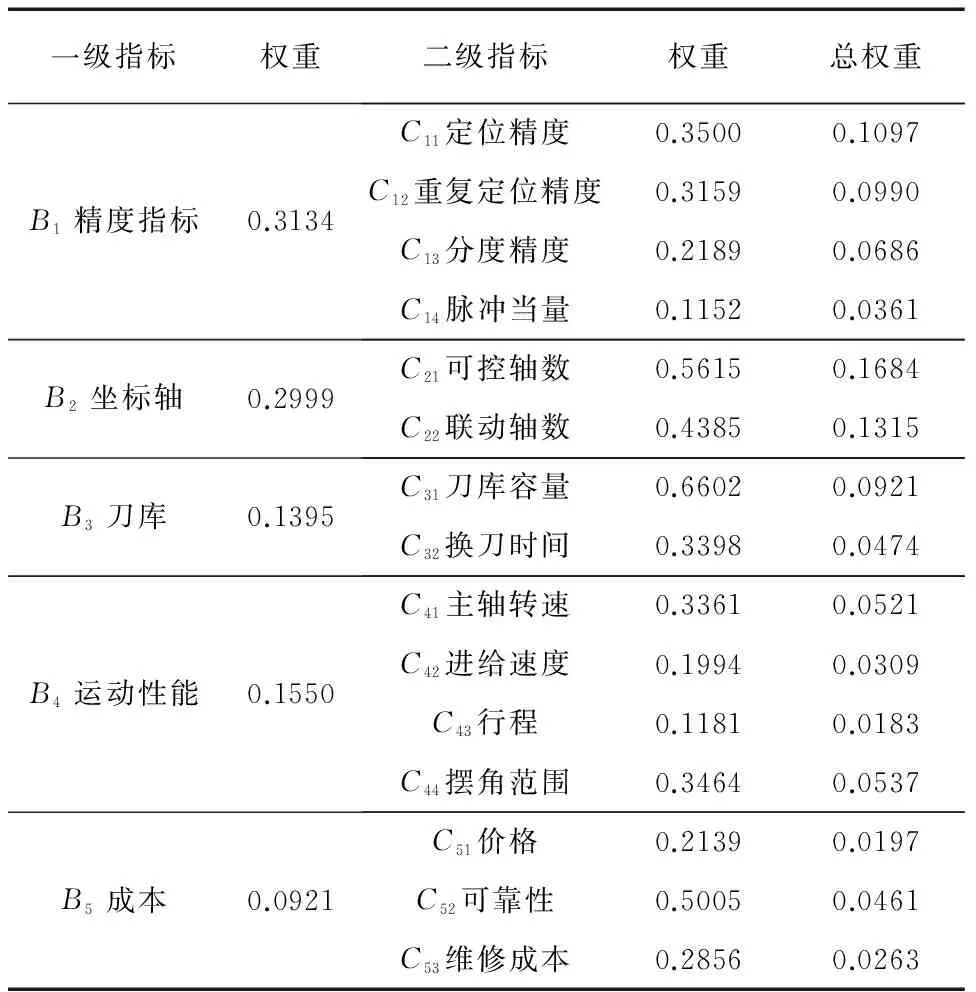
一级指标权重二级指标权重总权重B1精度指标0.3134C11定位精度0.35000.1097C12重复定位精度0.31590.0990C13分度精度0.21890.0686C14脉冲当量0.11520.0361B2坐标轴0.2999C21可控轴数0.56150.1684C22联动轴数0.43850.1315B3刀库0.1395C31刀库容量0.66020.0921C32换刀时间0.33980.0474B4运动性能0.1550C41主轴转速0.33610.0521C42进给速度0.19940.0309C43行程0.11810.0183C44摆角范围0.34640.0537B5成本0.0921C51价格0.21390.0197C52可靠性0.50050.0461C53维修成本0.28560.0263

可得方案1二级指标总权重矩阵为:

4.2 方案排序

为评价结果尽量具有客观性，选取技术人员、高校专家及操作工人共20人组成评审团。向评审团提供四种加工中心的技术参数，通过问卷调查法，由评审团对四种方案的二级指标做出评价。对问卷进行统计和分析后得到方案1的评价结果如表3所示。

表3 方案1模糊评价结果

可得到方案1的隶属度矩阵：

根据公式(12)可求得方案1的得分为72.4437分，同理可得其他方案的分数，方案2得分69.2123分，方案3得分65.7858分，方案4得分75.1211分。排序为方案4>方案1>方案2>方案3，方案4为最优方案。

5 结束语

加工中心相比较于传统数控机床能够加工更为精密的零件，且加工过程更为方便快速，在制造业内得到越来越广泛的使用。选购加工中心时，不仅需要综合考虑其各方面使用性能，还需要考虑其可靠性及维修维护成本等因素。将群组层次分析法与模糊评价法结合，综合考虑以上影响因素，提升评价结果客观性、可行性，最终选择出最优方案。

群组层次分析法将复杂问题划分为简单的具体指标，结合多名专家的评判意见，实现定性分析与定量分析相结合。同时该方法可方便的使用yaahp软件进行计算，矩阵计算可利用matlab实现，节省大量计算时间，提高了该方法的易用性。

[1] 吴星. 数控加工中心的可靠性分析与增长研究[J]. 广西民族大学学报(自然科学版), 2016, 22(1): 83-85,90.

[2] 赵万华,张星,吕盾,等. 国产数控机床的技术现状与对策[J]. 航空制造技术,2016(9):16-22.

[3] 孙宏才,田平,王莲芬.网络层次分析法与决策科学[M]. 北京:国防工业出版社,2011.

[4] 米长富,田建平,杨海栗,等. 基于模糊综合评判的机床设备选型研究[J].组合机床与自动化加工技术,2012(7):109-112.

[5] 陈婀娜. 基于灰色系统理论的数控机床选型决策[J]. 微计算机信息,2006,22(18):138-139,276.

[6]CTChen.ExtensionsoftheTOPSISforgroupdecisionmakingunderenvironment[J].FuzzySetsSystems,2000,114:114-121.

[7] 王秋颖,王福林. 灰色关联度分析法在农机设备评价选型中的应用[J]. 农机化研究,2014(8):46-48, 58.

[8] 叶义成,柯丽华,黄德育.系统综合评价技术及其应用[M]. 北京：冶金工业出版社，2006.

[9] 刘世豪,叶文华,唐敦兵,等. 基于层次分析法的数控机床性能模糊综合评判[J]. 山东大学学报(工学版),2010,40(1):68-72,92.

[10] 王宇,汪永超,牛印宝,等. 基于模糊层次分析法的数控机床设备优化选择[J]. 组合机床与自动化加工技术,2014(11):133-136.

[11] 龚艳,张晓,刘燕,等. 基于层次分析法的植保机械适用性综合评价方法[J]. 农业机械学报,2016,47(9):73-78.

[12] 赵楠,于爱兵,路明村. 机床造型质量的模糊层次综合评价[J]. 制造技术与机床,2007(9):66-69.

[13] 周海海,陈黎,胡伟峰. 整合DFMA的产品造型多元质量评价方法[J]. 机械设计与制造, 2012(6):285- 287.

[14] 周清华,杨萍,肖吉军,等. 基于层次分析法的包装质量分析[J]. 包装工程,2015,36(1):145-150.

(编辑 李秀敏)

Procurement Scheme Decision of Machining Center Based on Group Analytic Hierarchy Process

QIN Zhi-yuan， HUANG Hai-song， ZHANG Hui

(Key Laboratory Advanced Manufacturing Technology Ministry of Education，Guizhou University, Guiyang 550025,China)

Machining center is a key equipment in the manufacturing, making its procurement scheme decision need to consider various influence factors comprehensively. Combined group analytic hierarchy process and fuzzy evaluation method to make the decision more objective and feasible, and five aspects including accuracy indexes, axis, tool changer, movement performance and cost were analyzed. Firstly established evaluation system in the yaahp software to get the index weight, then established the fuzzy evaluation matrix to determine the index membership degree and index score, next, chose the optimal solution according to the score, finally the feasibility of this method were validated by an instance.

machining center; group analytic hierarchy process; fuzzy evaluation

1001-2265(2017)05-0157-04

10.13462/j.cnki.mmtamt.2017.05.042

2016-08-08；

2016-09-07

贵州省自然科学基金项目(黔科合J字[2015]2043号)；贵州省重大基础研究项目(黔科合JZ字[2014]2001)

秦志远(1991—)，男，山东泰安人，贵州大学硕士研究生，研究方向为数字化设计制造，制造业信息化，(E-mail)Zhiyuan_Qin1992@163.com。

TG659;TH162

A