基于位置姿势控制的并联机械手运动误差仿真分析*

朱向楠，韦源源

(1.扬州工业职业技术学院智能制造学院，江苏 扬州 225127； 2.扬州大学机械工程学院，江苏 扬州 225000)

0 引言

机械手是可以替代人类劳动进行自动化生产的机器，不仅使企业的生产总量发生了根本性变化，而且对人类的生活也产生了重大的影响。机械手具有生产效率高、成本低及承载力大等许多优点，广泛用于煤矿开采、汽车生产、海底探测和医疗手术等许多领域[1-2]。机械手技术的先进程度主要体现在控制系统性能上，因此，机械手的发展历史就是控制系统的发展历史。国内机械手控制系统近几年得到了迅速的发展，有些学者对当前的先进机械手进行了研究和探讨，为今后的研究奠定了理论基础。但是，当前的机械手控制理论的关键问题研究的还很初浅，核心技术需要更深入的研究。

为了降低并联机械手控制系统输出误差，许多学者对其控制系统展开研究。文献[3-4]研究了并联机械手控制系统的优化方法，采用遗传算法对并联机械手关节力矩进行优化，通过MATLAB软件对致动力矩进行仿真，从而降低并联机械手致动力矩。文献[5-6]研究了车载机械手PLC控制系统，分析了控制系统的硬件和软件，设计了四自由度车载机械手控制系统，具有较高的应用价值。文献[7-8]研究了并联机器人结构设计与控制，推导出机械手奇异位置和速度变化方程式，通过实验验证机械手轨迹跟踪效果，提高轨迹跟踪精度。但是，以前研究的并联机械手在受到外部载荷影响时，其位置姿势跟踪误差就会增大，从而影响并联机械手生产精度。

本文建立了并联机械手运动简图，推导出并联机械手位置姿势变化方程式。引用模糊PID控制器，采用前馈补偿原理对模糊PID控制器进行改进，通过仿真验证改进后的控制系统输出误差，为提高并联机械手控制系统跟踪精度提供理论参考价值。

1 并联机器人数学模型

1.1 机械手运动学建模

本文研究的是二自由度并联机械手模型如图1所示。机械手由矩形板、液压缸为圆柱接头(CJ)、回转接头(RJ)、球形接头(SJ)、比例阀(PV)、线性可变差动传感器(LVDT)、齿轮泵(P)、电动机、减压阀、液压动力组件、液压过滤器等组成。机械手的顶板尺寸为L×B，它通过RJ和SJ连接到液压缸的活塞上，RJ轴与SJ之间的距离为L。液压活塞缸系统的圆柱接头1，圆柱接头2分别定义为CJ1和CJ2。圆柱接头CJ1和CJ2的移动可分别通过弹簧中心电磁阀操作的比例阀1(PV1)和比例阀2(PV2)的滑阀移动来控制。比例阀PV1、PV2的阀芯运动可以通过来自控制器的指令电压信号e=[e1e2]T来控制。CJ的相对运动方向通过LVDT反馈信号决定的。

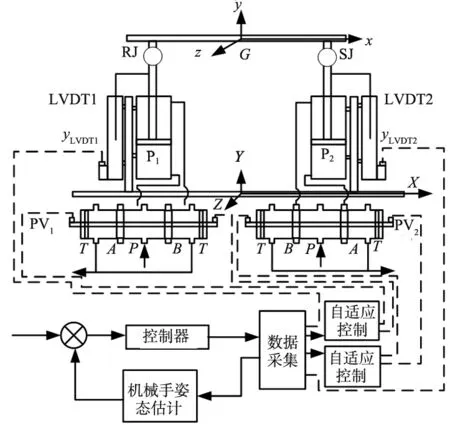
图1 液压驱动并联机械手简图

二自由度并联机械手的运动学图如图2所示。在并联机器人的底座上，将固定坐标系定义为O-XYZ，将机械手顶板坐标系定义为G-xyz。在不同时刻，由于起伏和俯仰运动，并联机械手新的位置也在改变。通过运动定义的G′-x′y′z′坐标系，从而得到顶板重心的新位置。在俯仰运动后，获得板RJ″和SJ″的最终方向，并获得相应的末端执行器拟合坐标系x″y″z″。

图2 并联机械手运动图

末端执行器关节Rj的位置矢量[9]可以表示为：

Rj=RG+rj

(1)

(2)

式中，RG为机械手顶板重心矢量位置；rj为机械手关节相对于xyz坐标系的位置矢量。

机械手在SJ处的位移与升沉和俯仰运动相关，其变化关系式为：

ΔRj=ΔRG+Δrj

(3)

(4)

式中，ΔRj=Rj″-Rj；ΔRG=RG″-RG；Δrj=rj″-rj。

末端执行器关节速度可以表示为：

(5)

式中，ωp为末端执行器顶板的角速度。

末端执行器关节加速度可以表示为：

(6)

式中，αp为末端执行器顶板的角加速度。

垂直固定双作用单杆液压缸立柱为二自由度并联机械手。液压并联机械手的腿为圆柱关节。并联机械手的腿液压执行机构系统的动力学模型可以表示为：

(7)

(8)

式中，yi、vi和ai分别为机械手第i腿运动位移，速度和加速度。

由于机械手的腿被设置为刚性，并联机械手的垂荡和俯仰运动可以通过圆柱关节活塞的运动表示为：

(9)

(10)

式中，h为垂荡位移；θr为执行器的俯仰角。

垂荡速度和加速度可以表示为：

(11)

(12)

顶板的角速度和角加速度可以表示为：

(13)

(14)

末端执行器可以自由移动的区域为机械手的工作空间。执行器的升沉和俯仰极限可由机械手腿的圆柱关节运动的最大和最小测量值来估计，YLVDT1和YLVDT2分别为腿1和2与机械手腿的圆柱关节的轴之间的距离。

1.2 机械手动力学建模

根据牛顿-欧拉方法[10]可知，广义的动力方程可以写成：

(15)

式中，M、N、G和q分别为惯性质量、离心科里奥利力和摩擦力、重力矩阵和位置矢量。

机械手各支腿的动力学方程可以写成：

(16)

Fji=Ffi+Ffpi

(17)

式中，Fji为关节摩擦力；Ffi为圆柱关节摩擦力；Ffp为旋转关节摩擦力或球形关节摩擦力。

机械手顶板的惯性力和外部载荷定义为：

FI=FIr+FIl

(18)

(19)

(20)

(21)

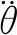
在本系统中，机械手的运动由液压缸活塞的运动获得。液压缸的压力动力学方程可以写成：

(22)

(23)

式中，P1i和P2i分别为气缸室1和2中的压力；Aa1i和Aa2i分别为活塞有杆端和无杆端面积；β为油的体积模量；V10i和V20i分别为1和2液压缸的初始容积；Q1i和Q2i分别为1和2液压缸的流量。

阀门流量与电磁阀激励电压之间关系式为：

(24)

式中，Cl为泄露系数；Cv1、Cv2为阀门主流量系数。

机械手旋转关节或销关节的法向力:

(25)

其中，

(26)

δ=0.01×(1-cosθ)L/2

(27)

(28)

式中，FN为法向力；d1和d2为不同球形的直径；vk为不同接头金属硬度比；Ek为杨氏模量。

关节接触的合力表达式为：

Ffp=Ffjsinθ+FNcosθ

(29)

式中，Ffp为关节接触的合力；Ffj为活塞运动摩擦力；FN为活塞垂直方向的力。

2 控制器设计

2.1 模糊PID控制

传统模糊PID控制过程如图3所示。

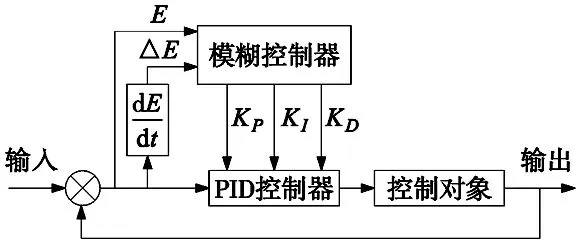
图3 模糊PID控制

根据输入输出误差和误差变化率，对PID控制器参数KP、KI、KD进行调整，使模糊集的论域都能涉及到各个参数变量。模糊集的输入和输出量的论域定义如下：E的范围为[-1,1]，ΔE的范围为[-35,35]，KP的范围为[12,12]，KI的范围为[-4,4]，KD的范围为[-0.1,0.1]。为了使模糊控制精度达到最优，将模糊子集定义为7个语言值，分别为：①负大(NB)；②负中(NM)；③负小(NS)；④零(ZO)；⑤正小(PS)；⑥正中(PM)；⑦正大(PB)。通过模糊集的7个语言值调节PID控制器输出误差。

PID控制调整参数[11]定义为：

(30)

式中，KP(k)、KI(k) 、KD(k)分别为当前PID控制器的比例、积分和微分控制参数；KP0(k-1)、KI0(k-1) 、KD0(k-1)分别为前一刻PID控制器的比例、积分和微分控制参数；ΔKP(k)、ΔKI(k) 、ΔKD(k)为模糊控制器的输出控制参数。

2.2 前馈补偿原理

采用前馈补偿方法可以有效地降低控制系统稳态误差，对外界环境的变化起到抑制作用，其补偿控制原理如图4所示。

图4 前馈补偿简图

在图4中，N(s)为外界环境所干扰的力矩，G1(s)、G2(s)为传递函数，Gn(s)为补偿函数，通过合理的设计Gn(s)，使其对输出函数进行补偿，从而抑制外界环境的干扰对C(s)的影响。

根据补偿控制原理[12]分析可知：外界环境干扰产生的误差变化方程式为：

(31)

随着模糊PID控制参数的变化，Gn(s)也随着改变。定义PID控制器速度调节传递函数表达式为：

(32)

因此，可以推导出Gn(s)传递函数表达式为：

(33)

2.3 模糊前馈PID控制器

本文将自校正前馈模糊PID控制器应用于液压驱动并联机械手的位姿控制，机械手的姿态要求、响应和误差可以表示为：

(34)

通过模糊逻辑来估计PID控制器增益，总电压e可以表示为矩阵形式如下：

(35)

式中，eff为前馈电压；eb为偏压；efp为模糊整定PID电压。

电压信号定义为：

(36)

(37)

二自由度并联机械手采用模糊前馈PID控制流程如图5所示。

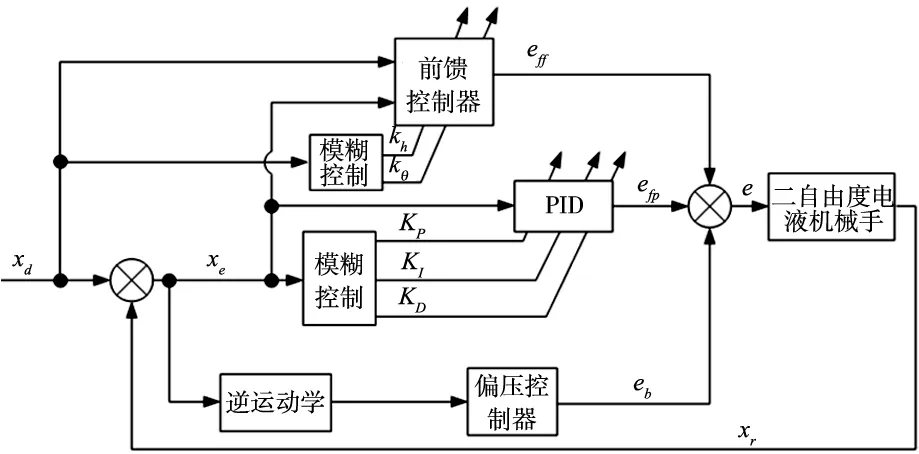
图5 机械手模糊前馈PID控制流程

3 运动仿真

为了比较并联机械手运动误差跟踪效果，采用MATLAB软件对机械手运动位移和角位移跟踪进行仿真。假设机械手期望运动位移和角位移分别如图6、图7所示。仿真参数设置如下：顶板长度L=0.6 m，顶板宽度B=0.3 m，顶板质量mp=100 kg，无杆腔活塞面积Aa1i=1.25×10-3m2，有杆腔活塞面积Aa2i=9.42×10-4m2，活塞质量mai=1.5 kg，油体积模量β=1.4×109Pa，无杆腔初始容积V10i=1.25×10-4m3，有杆腔初始容积V20i=9.42×10-4m3。在外部载荷50 kg干扰下，采用模糊PID控制和模糊前馈PID控制输出的误差分别如图8和图9所示。在外部载荷100 kg干扰下，采用模糊PID控制和模糊前馈PID控制输出的误差分别如图10和图11所示。在外部载荷150 kg干扰下，采用模糊PID控制和模糊前馈PID控制输出的误差分别如图12和图13所示。

根据图8和图9所示，并联机械手在受到外部载荷50 kg干扰下，采用模糊PID控制方法，机械手运动位移和角位移跟踪误差最大值分别为2.3 mm和2.0×10-3°；采用模糊前馈PID控制方法，机械手运动位移和角位移跟踪误差最大值分别为1.1 mm和1.2×10-3°。根据图10和11所示，并联机械手在受到外部载荷100 kg干扰下，采用模糊PID控制方法，机械手运动位移和角位移跟踪误差最大值分别为3.8 mm和2.8×10-3°；采用模糊前馈PID控制方法，机械手运动位移和角位移跟踪误差最大值分别为1.5 mm和1.4×10-3°。根据图12和图13可知，并联机械手在受到外部载荷150 kg干扰下，采用模糊PID控制方法，机械手运动位移和角位移跟踪误差最大值分别为5.3 mm和3.9×10-3°；采用模糊前馈PID控制方法，机械手运动位移和角位移跟踪误差最大值分别为2.2 mm和1.9×10-3°。

因此，并联机械手随着外部干扰载荷的增大，机械手输出的位移和角位移跟踪误差也会增大。但是，采用模糊前馈PID控制方法，机械手在受到不同外载干扰条件下，机械手输出的运动位移误差和角位移误差较小，自适应能力较好，从而抑制外界环境的干扰。

图6 运动位移 图7 运动角位移

图8 运动位移误差(50 kg) 图9 运动角位移误差(50 kg)

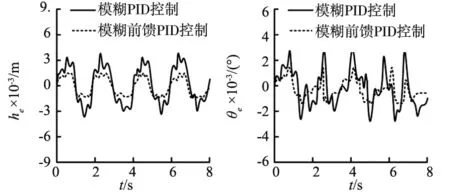
图10 运动位移误差(100 kg) 图11 运动角位移误差(100 kg)

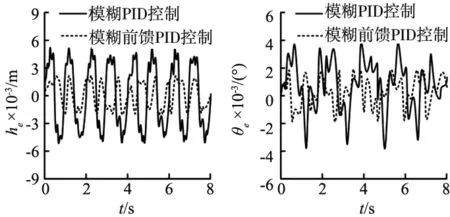
图12 运动位移误差(150 kg) 图13 运动角位移误差(150 kg)

4 结束语

针对并联机械手采用传统模糊PID控制系统输出误差较大问题，设计了自整定模糊前馈PID控制系统，并对并联机械手在不同外部负载条件下进行误差仿真，主要结论如下：

(1)并联机械手采用模糊PID控制系统，其运动位移和角位移输出误差较大，自适应调节能力较弱，而采用模糊前馈PID控制系统，其运动位移和角位移输出误差较小，自适应调节能力较强。

(2)在不同外部负载条件干扰下，随着外部负载力的增大，并联机械手运动位移和角位移跟踪误差也会随着增大，通过MATLAB软件可以对不同外部负载干扰情况进行仿真验证，可以检验跟踪效果。

(3)本文研究的并联机械手运动位移和角位移跟踪误差，在未来企业中具有一定的应用价值，并没有研究机械手力矩跟踪误差，未来可以作为进一步研究对象。