基于WPD-CNN二维时频图像的滚动轴承故障诊断*

陈里里，付志超,凌 静,董绍江

(1.重庆交通大学 a.机电与车辆工程学院；b.城市轨道车辆系统集成与控制重点实验室，重庆 400074;2.重庆市勘测院，重庆 400020)

0 引言

滚动轴承作为旋转机械设备中广泛应用的基本部件，随着对旋转机械速度、载荷的要求越来越高，滚动轴承工作状态直接影响并决定着整个机器的性能安全[1]。同时，滚动轴承故障的发生，不仅会带来巨大的经济损失，甚至会给操作人员带来安全隐患。据统计，在旋转机械中，约30%的机械故障与滚动轴承损坏有关[2]。因此，对滚动轴承进行有效的状态监测具有重要意义，可以尽早诊断出故障，从而降低维护成本，最大程度地减少停机时间并防止灾难性损坏。

目前国内外在对滚动轴承故障诊断的研究过程中, 首先对故障信号进行特征向量的提取, 再通过分类器对不同振动信号的特征向量进行模式识别，可实现不同类型的轴承故障诊断[3]。陈剑等[4]利用基于 IVMD和马田系统的方法实现滚动轴承的故障诊断。汪朝海等[5]提出基于经验模态分解与主成分分析的滚动轴承故障诊断方法。戴洪德等[6]提出一种基于平滑先验分析和排列熵的方法对滚动轴承故障进行了识别诊断。尽管传统的智能方法在滚动轴承故障诊断领域取得了显著成就，但所提取的信号特征属于浅层结构，存在一定的局限性，并且选择的信号特征很大程度上取决于研究人员的先验知识，可能导致有效特征信息的丢失。因此需要使用先进的信号处理技术对故障信号进行特征提取，来代替自适应地手动提取和选择特征。

深度学习(DL)具有自动提取原始数据的分层表示特征的优势，因而在故障诊断领域中显示出良好的前景[7]。Jia F等[8]提出了一种基于堆叠式自动编码器的DNN，用于滚动轴承和行星齿轮箱的故障诊断。Liu RN等[9]将CNN引入故障诊断以直接处理一维振动信号，并取得了良好的效果。Zhang W等[10]构建了一个基于DNN的堆栈去噪自编码器，以较低的信噪比诊断故障信号。在实际应用中，旋转机械的轴承在复杂的环境中连续工作，振动信号不稳定，而故障特征则合并在高噪声环境中。 在这种情况下，如果只是从单一的时域或频域中学习故障特征，使用一维信号进行故障诊断的难度将会增加。

本文提出的方法中，小波包分解能无冗余地提取非平稳信号的时频特征，时频分辨率更加精细，有效解决小波变换高频低分辨率的不足，相较于一维信号，时频图像可以显示更多有效特征[11]。同时卷积神经网络[12]被广泛用于图像处理领域，WPD-CNN模型可以自动提取图像特征并在Softmax分离器实现分类，减少计算复杂度并提高诊断精度。实验表明，在对不同故障类型的滚动轴承的诊断中，所提方法能有效地分类并达到很好的效果。

1 时频图像生成原理

小波包分解能够同时对信号的高频和低频部分进行分解，具有无冗余、无疏漏分解和准确重构的特点[13]，因此本文采用小波包分解将一维轴承信号转换为二维时频图像，通过对信号进行有效的可视化处理，极大地提高了WPD-CNN模型的识别精度。小波包分解可以通过一对低通和高通小波滤波器实现，分别表示为hk和gk。hk是缩放函数的两尺度展开系数，也称为低通滤波器系数。gk是二阶方程的小波展开系数，也称为高通滤波器系数。gk和hk的关系可以表示为：

gk=(-1)k-1h1-k,k∈Z

(1)

小波包分解公式如下：

(2)

(3)

本文对滚动轴承信号H(0，0)进行小波包3层分解，得到23个低频分量和高频分量，从左到右频率依次增高，小波包分解树形结构如图1所示。

图1 小波包分解树

2 WPD-CNN模型原理

2.1 CNN

卷积神经网络被认为是最有效的前馈监督机器学习网络之一[14]。在图像识别领域具有强大的特点和优势，因此本文采用这种端对端的方法，省去人为提取特征的步骤。标准的CNN模型结构如.所示。以三层CNN(即输入层，隐含层和输出层)为例，其中S和N分别是输入和输出向量，隐含的矢量用H表示。前馈方法如下所示：

H=σ(ω1S+β1)

(4)

N=σ(ω2H+β2)

(5)

其中，ω1是输入层和隐含层之间的权重矩阵，ω2是隐含层和输出层之间的权重矩阵。 隐含层和输出层的偏置矢量分别表示为β1和β2。为缩短模型训练时间，避免出现梯度消失的问题，本文采用线性整流函数ReLU作为激活函数，有：

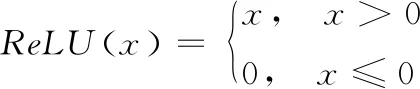
(6)

网络的损失函数如下所示：

(7)

其中，mi代表目标向量，n代表训练样本的数量。 该网络的目标是通过反向传播和梯度下降(GD)来使损失函数FL最小化。 在误差的反向传播过程中，在本文提出的WPD-CNN网络模型中，随机梯度下降法(SGD)被用于调整网络自适应参数。

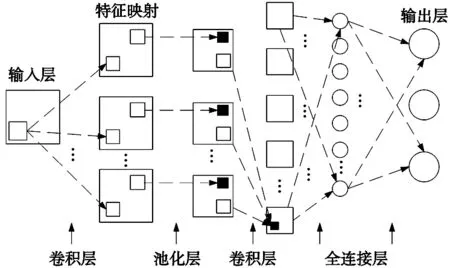
图2 CNN结构模型

2.2 VGG19网络模型

VGG19是由ImageNet数据集训练的深度CNN模型，预训练的VGG19模型可以被应用于许多图像识别任务的特征提取器，并取得了惊人的性能。 VGG19模型结构如图3所示。

图3 VGG19 模型结构

在本文提出的故障诊断模型中，VGG19被用作初始轴承二维时频图像特征提取器。为减少训练时间，通过微调将预训练的VGG19前5层(C1，C2，C3，C4和C5)的参数迁移到WPD-CNN模型中，并进行微调，以适应输入的轴承故障时频图像，从而提高轴承故障诊断的预测效果。特征提取后，将全连接层(Fc8)形成的分布式特征表达输入Softmax分类器进行训练。

3 基于WPD-CNN的轴承故障诊断方法

本文所提出的基于WPD-CNN的轴承故障诊断方法过程如下：首先利用WDP将信号中的时频特征充分展现进行时频图像生成。然后将WPD-CNN网络结构用于时频图像特征提取，避免了人工特征提取的主观性，并减少了计算量。最后用提取的特征进行分类器的训练，完成故障诊断任务。提出方法的流程图如图4所示。其步骤如下：

(1)采集噪声环境下轴承的振动信号，对每一类原始故障数据进行连续截断处理，构造样本矩阵。

(2)应用WPD将截断信号转换为二维时频图像，将其分为训练集和测试集。

(3)将训练集输入WPD-CNN模型进行训练。

(4)输入测试集进行测试，得到分类结果。

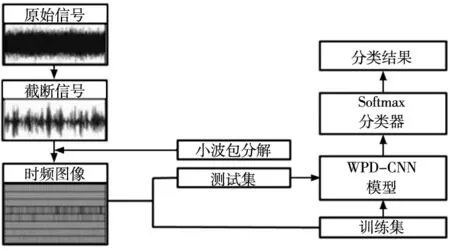
图4 故障诊断流程图

4 轴承实验研究与分析

4.1 实验数据

本文用于验证所提出方法性能的滚动轴承数据来自美国凯斯西储大学(CWRU)。实验数据故障类型分为内圈故障、外圈故障、滚动体故障、正常轴承4种类型，数据采样频率为 12 kHz，电机负载 1 hp，电机转速 1772 r/min。采用制造商SKF的6205-2R型深沟球轴承的驱动端加速度数据，通过放电加工将单点故障引入到测试轴承的内圈，滚动元件和外圈中，其中故障深度为0.011 mm,故障直径分别为 0.007、0.014、0.021 mm共10 类轴承故障类型。滚动轴承数据集具体描述如表1所示。

表1 滚动轴承数据集描述

图5是1 hp 负荷下故障尺寸为 0.07 mm 的轴承部件在不同故障状态下的故障信号的时域波形。从该图中可以看出，仅依靠信号波形图很难判断滚动体的故障类型，因此需要对故障信号进行进一步的时频分析。

(a) 内圈故障 (b) 滚动体故障

图6是图5中不同故障类型对应的小波包分解时频图，由图可知，正常轴承信号主要集中在低频段，而其他类型的故障主要分布在中频段，且在各频段范围内，能量分布特点也存在着明显差异。因此，不同故障信号在小波包分解时频图中，振动信号包含的特征信息得到充分展现。

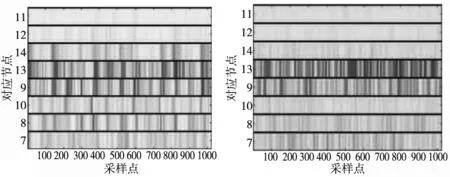
(a) 内圈故障 (b) 滚动体故障

4.2 诊断结果分析

将二维时频图像数据集随机分为两部分：900张训练集和300张测试集。将数据集输入到WPD-CNN模型中，经过特征提取之后，将特征输入到Softmax分类器进行故障分类。混淆矩阵是评估分类算法性能的有效可视化工具。实验得到的混淆矩阵如图9所示。可以看出，除了 B021、IR007、OR014故障类型轴承诊断的正确率没有达到100%外，剩下的 7类故障类型准确率均达到100%。

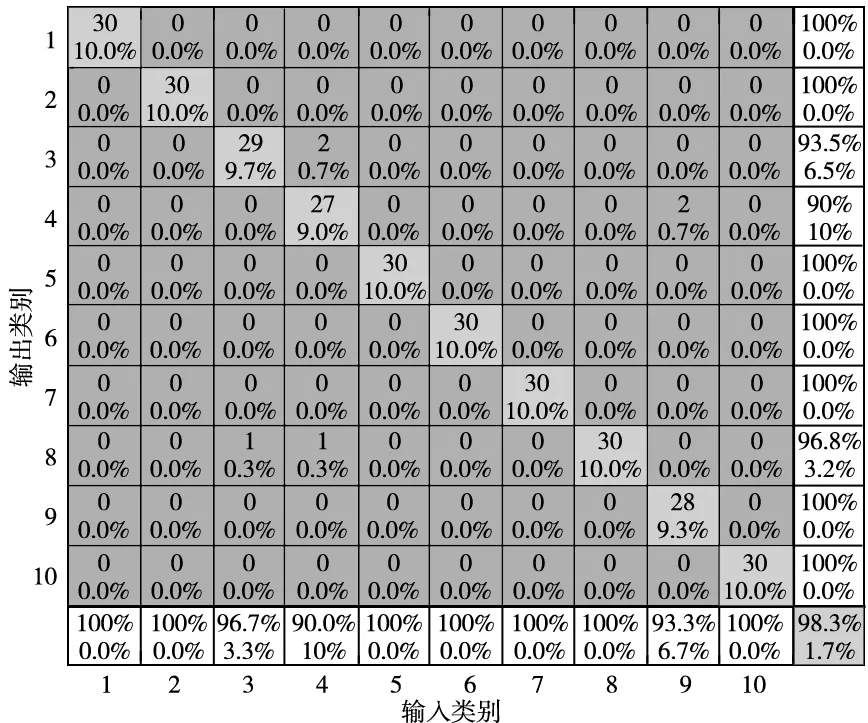
图7 模型混淆矩阵

图8显示了使用WPD-CNN模型在每次迭代中的训练精度和损失值。本文提出的模型在少量迭代中实现了较高的准确性和最小的损失。由于模型在初始权重中使用VGG19模型的权重迁移，训练时间显著减少，并且轴承故障诊断的预测效果得到改善。

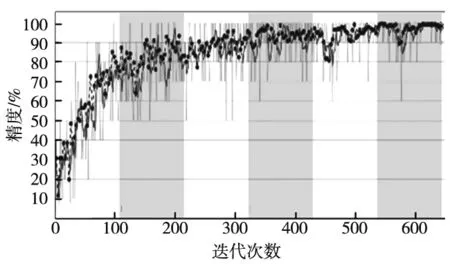
图8 迭代训练损失值和精确率

4.3 模型对比分析

为了对比所提方法的稳定性和诊断的准确性，分别与文献[15]中手动提取特征+支持向量机分类器(FT-SVM)模型，文献[16]中的堆叠自编码器深度模型+Softmax分类器(SAE-SMC)模型作比较。对每种方法进行20次随机试验，每次试验的准确率如图9所示。可以看出，所提方法在20次随机试验中不仅准确率高于传统方法和深度学习分类模型，且稳定性更好。模型诊断结果如表 2所示。WPD-CNN模型的平均正确率均高于 FT-SVM、SAE-SMC模型,且平均正确率达到了98.343%，所以所提方法能够有效作为滚动轴承故障诊断的模型。

表2 不同模型平均准确率

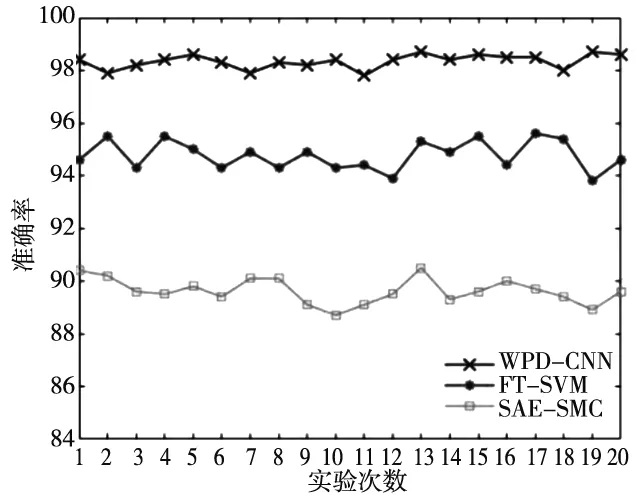
图9 随机实验准确率

5 结论

本文提出了一种基于WPD-CNN二维时频图像的新型滚动轴承故障诊断模型，以检测复杂环境下滚动轴承的故障类型。主要优势包括将传统的一维振动信号特征提取问题转换为二维图像处理问题，有效避免了传统方法中特征选择的不确定性对故障诊断的影响，增强了诊断过程的智能化。实验结果表明，在轴承信号故障诊断领域，本文提出的基于时频图像的诊断模型与传统方法相比具有更好的性能，在凯斯西储大学(CWRU)数据库中的10类不同位置的滚动轴承故障信号测试中，故障识别率均远高于其他先进模型。为提高模型的准确率、收敛性、鲁棒性，在后续研究中，将通过参数寻优和模型训练，继续改进模型。