基于双树复小波和AR谱的滚动轴承故障诊断*

宋玉琴，周琪玮，赵 攀

(西安工程大学电子信息学院，西安 710600)

0 引言

滚动轴承是各种生产设备的重要组成部分且长期在高速、高负载情况下工作，对其故障识别能够大幅降低产品的次品率和减小设备维护造成的经济损失。因此，自动并有效地对滚动轴承故障进行诊断有着重要的意义[1]。

分析滚动轴承振动信号获取滚动轴承的状态信息，为在多种故障信号的情况下准确区分具体故障类型提供帮助。虽然振动信号存在时域非平稳特性和频域非线性特性，但信号处理技术已经日趋成熟，能够高效地揭示振动信号的时域特性、频域特性以及二者之间的联系[2]。

传统时域信号处理方法基于信号自身的时域特性，通过数学计算提取各种信号时域特征。文献[3]分析了滚动轴承故障信号的时域波形和3个时域指标，但时域指标的选择具有经验性。文献[4]使用离散小波变换(DWT)对轴承滚动体故障进行特征提取。特征送入分类器后分类准确率相较于传统方法有着较高的提升，但遗漏采样间隔内的特征信息，变换后的子信号存在频率混叠问题。小波包变换是在小波多分辨分析的基础上发展完善而来，为解决小波分辨率不足、低频段信号时间分辨率不佳等问题[5]。文献[6]利用小波包将信号分解后再求取能量谱，得到稳定性较高的小波包节点能量特征，但依然没有解决采样间隔的信息遗漏和频率混叠。

针对上述问题，本文提出幅频对比算法优化的DTCWT结合AR功率谱的滚动轴承故障诊断方法。DTCWT优异的低频分辨率和改善频率混叠的能力保证了信号特征的完整提取，幅频对比算法进一步削减虚假、错误频率信息，而AR功率谱能深刻、集中体现信号的频率功率分布，有效地提取复杂故障的典型特征信息。

1 幅频对比算法优化的DTCWT

DTCWT是由Kingsbury等人提出，具有近似平移不变性和改善频率混叠等优良特性[7-8]，改善和解决小波变换存在的频率混叠、采样间隔信息丢失等缺陷。

1.1 DTCWT

DTCWT采用二叉树结构的设计方法，两个分支树使用平行但不同的低通和高通滤波器，一路生成实部树，另一路生成虚部树[9]。为获得更好的对称性，一路分支树的滤波器长度为奇数，另一路为偶数。两个分支树滤波器之间延迟一个采样间隔，实部树遗漏的采样值就能被虚部树采集，不会丢失原始信号含有的隐藏信息。

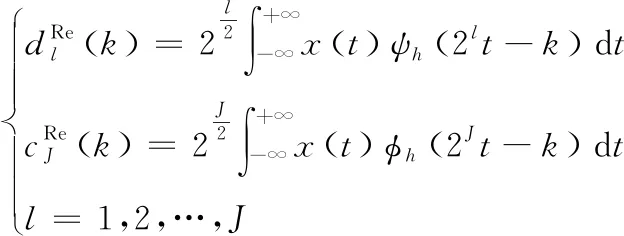
(1)

最终由两树组成的DTCWT输出复合序列如下：

(2)

为确定DTCWT的分解层数和验证改善频率混叠的能力，构造仿真信号进行试验，见式(3)：

y=0.5sin(200πt)+sin(400πt)+

1.3sin(600πt)+0.7sin(800πt)

(3)

式中，时间t为1 s，采样点数为1024，采样频率为2048 Hz，时域波形与频率特性如图1所示。

(a) 时域图

DTCWT分解层数与误差和耗时的关系如图2所示。在仿真信号相同的条件下，消耗时间在分解层数为6层时达到稳定，并不会持续增加；误差不会因为分解层数的增加而持续减小。综合考虑误差和耗时两个因素，选择层数为4层。

图2 DTCWT分解层数与误差和耗时的关系

分解层数确定为4层，分别使用DTCWT和DWT对仿真信号y进行子频带分解和重构，频率特性如图3所示。

(a) DWT (b) DTCWT

图3a中，仿真信号经antoni9_7滤波器4分解后，在第1层频带子信号中除了200 Hz、300 Hz和400 Hz的固有频率外，还出现112 Hz、212 Hz和312 Hz的虚假频率，212 Hz的振幅甚至高于固有频率200 Hz的幅值，在其他层中也出现较多虚假频率和频率混叠现象。图3b中，经长度为9和7的near-symmetric双正交滤波器和长度为14的正交Q-shift-14希尔伯特小波滤波器4层分解后，4层频带子信号频率与仿真信号固有频率一致。滤波器的非理想截止特性使第1、4层出现混叠现象和振幅微弱的虚假频率，但依然验证了它抑制虚假频率、改善频率混叠的能力。

1.2 幅频对比算法

针对DTCWT得到的频带子信号中依然存在的虚假频率和频率混叠的问题，采用幅频对比算法计算幅频特性进行优化，其思想为：

图4 幅频对比算法优化的DTCWT流程图

(1)频带子信号的幅值、频率与原信号的幅值、频率对比，保证固有频率的幅值在子信号中占比最高；

(2)频率标准差(RVF)可以反映频率的分散程度，与频带子信号的离散程度为正比关系，间接表征频带子信号中含有频率值的数量。

快速傅里叶变换(FFT)能够准确分析信号幅频特性[10-11]，是实现此算法基本运算的理想工具。幅频对比算法优化DTCWT的流程如图4所示。

图4中判定条件(a)和(b)如式(4)、式(5)所示：

(4)

(5)

式中，fi和qi分别表示i时刻频谱对应的频率值及幅值；Fi和Qi分别为i时刻原信号频谱对应的频率值及幅值；N为频谱的频率数；fc为平均频率。

2 AR功率谱

原始信号经过频域参数优化的DTCWT后，得到K-1层频带子信号，如果计算各频带子信号的时频域参数会使特征维数升高，增加计算和诊断成本，需引入其他分析方法。AR功率谱充分结合AR模型的线性外推、频率定位准确特性[12]和信号功率信息，得到各层频带子信号的功率和，将其作为特征表征不同信号隐含的典型信息。

AR谱估计的流程为：

(1)对频带子信号建立AR模型，得到AR系数；

(2)利用AR系数建立该频带子信号的线性预测重构信号；

(3)计算重构信号功率谱，得到总功率。

AR模型的一般数学结构如式(6)：

(6)

式中，p为模型阶数；xr(m)是时间m的预测重构信号，与前p个预测值有线性关系；αk表征AR系数；ε(m)为误差项，表征真实值和预测值之间的差别。

AR模型的系数和功率谱的计算方法有多种，例如Yule-Walker，Burg，改进协方差和协方差法[13-14]，分析上述方法后，采用Burg法，无需估计自相关函数，从已知序列求得反射系数，用Levinson递推算法得到AR参数。

3 实验与评价分析

采用美国凯斯西储大学轴承数据中心的滚动轴承加速度振动信号对本文所提方法进行验证。电机驱动端轴承型号为SKF6205，包含9个滚动体。应用电火花技术人为制造不同故障直径，采集轴承在不同故障直径和故障位置的振动信号，采样频率为12 kHz。本实验采用的数据描述如表1所示。

表1 实验数据描述

支持向量机(SVM)是一种广泛应用于的小样本数据分类的分类器，主要是建立一个分类超平面作为决策面，最大限度地扩大正、负分离边的距离，惩罚因子等参数对最终的结果有着很大的影响[15]。参数的选择实质上属于组合优化问题，遗传算法能够自适应地寻找参数组合最优解，很好地解决此类问题，避免认为选择参数的盲目性。因此遗传算法优化的支持向量机(GA-SVM)作为分类器对提取的特征进行分类诊断。

3.1 幅频对比算法优化的DTCWT+AR谱

使用与1.1小节相同的双树复小波滤波器对全部实验信号进行4层分解，得到6400组数据，经过幅频对比算法后，数据量下降到4800组。

随机选取一个正常(Norm)振动信号，其频域特性如图5a，振幅最高的3个固有频率为87.89 Hz、1008 Hz和2000 Hz。图5b是幅频对比算法排除的信号的幅频特性，因为出现4324 Hz和5186 Hz的虚假频率，且振幅分别为2000 Hz的固有频率振幅的83.33%和61.11%，导致虚假频率的功率值在该层子信号中比重很高，若不排除此子信号，会获得错误的特征信息，影响最后的诊断结果。

(a) Norm信号频域图

图6是保留的频带子信号幅频特性，3层子信号将固有频率全部提取且振幅最大，保证功率占比最大，排除微弱频率的干扰。

图6 幅频对比算法保留的频带子信号幅频特性

得到优化的4800组样本后，利用AR模型取得信号的预测重构信号，包含当前时刻和前P个时刻信号的特征。AR模型阶数为10，采用Burg法得出AR系数和功率，将信号每个时刻的功率相加得到信号总功率，不需要复杂的计算和组合过程。

随机抽取所有类别各40组样本，得到的功率特征如图7所示，其中虚线圈中的局部放大如图8所示。

图7 幅频对比算法优化的DTCWT+AR谱的功率特征三维散点图

图8 幅频对比算法优化的DTCWT+AR谱的功率特征三维散点图局部放大

从图7中可以看出第1层子频带总功率为50(db/Hz)的平面分离出IF7、IF21、OF21、OF7与其他类型故障，IF7与OF21仅在小部区域有重叠；图8中，虽然BF21和IF14有个别特征点分散，但不同种类信号的特征类内分布集中，重叠区域仅存在于BF7与BF14之间，上述结果说明AR功率谱准确地提取隐藏在各个信号内部的功率信息，获得能直接、简洁地反映不同信号的总功率特征信息。准确得到总功率特征的前提是DTCWT提取各自信号的正确的频率信息。通过频带子信号与原信号的对比以及频率标准差(RVF)，经过幅频对比算法优化后DTCWT提高了改善信号分解过程中出现的频带子信号的频率混叠和虚假频率的能力，筛选的频带子信号包含了各自信号的正确的频率信息。其次，提取的10种故障类别特征值分布在(0～100)、(0～40)与(0～3)的大范围空间内，三层不同频带子信号总功率相互间的距离差异相差一个数量级，即使有个别特征值出现偏离和分散，也不会造成故障特征之间的混乱和重叠，这一结果表征AR功率谱计算的不同种类故障总功率特征可区分度高，适合作为代表不同故障信号特点的特征值，可以将其应用至滚动轴承故障诊断中。

3.2 DWT+显著时域特征

DWT+时域特征中小波滤波器与1.1小节一致。时域特征种类与诊断正确率不为正比关系，并不是越多越好[16]，文献[16]基于经验模态分解得出显著特征组合，在此基础上，结合DWT分解特性并分析频带子信号后，选择提取峭度(KV)、均方根(RMS)和方差(VAR)作为时域特征参数。

上述3种时域特征分别作为坐标轴，得到的时域特征空间相互关系如图9所示，虚线圈中的局部放大如图10所示。

从图9中得到，IF7、IF21、OF21和OF7故障虽然分离，但相互之间的峭度间隔只有1，方差的分布间隔只有0.4，分散点与其他特征混叠，易混淆不同类型特征。

图9 DWT+显著时域特征三维散点图

图10中6类故障信号的均方根和方差集中在0～0.04，与3.1节方法中分布最窄的第3层子频带信号相比，宽度仅为其1.33%，出现上述结果的原因在于DWT的频率混叠问题严重，分解频率的准确度低于DTCWT方法，使得各级频带子信号的主要频率相互混杂、叠加，振幅相近，没有达到预期的分解效果，造成提取的不同种类故障的时域特征间隔小，差异性低，无法区分代表性频率信息；再者，较多的虚假频率造成同一类故障中部分特征值分散，混淆、掩盖真实频率信息，在不同种类特征间隔很小的前提下，分散的特征值对整体故障诊断会造成较大影响，极易发生故障种类的错误诊断。

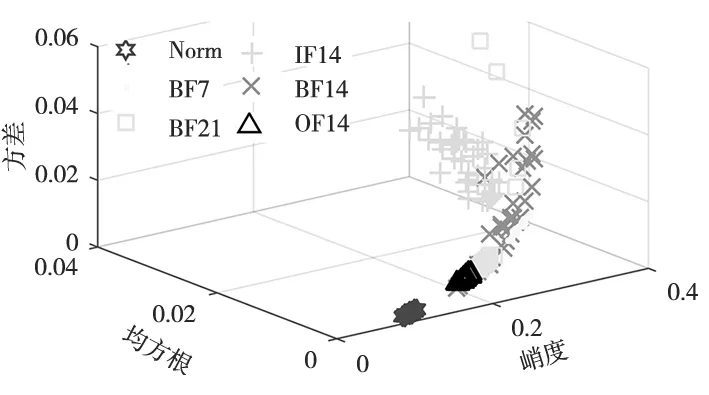
图10 DWT+显著时域特征三维散点图局部放大

3.3 DTCWT+组合时域特征

为与3.2小节使用的显著时域特征区分，在峭度(KV)和方差(VAR)基础上增加方根幅值(RA)和歪度(SKEW)。由于时域特征组合方式过于复杂和繁琐，且具有一定的经验性，故对上述4种时域特征进行适当组合。

第3.1小节方法与DTCWT+组合时域特征的诊断准确率如图11所示。

6种组合时域特征包含1种、2种和3种特征组合，从图11中分析可得：

(1)KV+VAR组合的诊断准确率明显高于SKEW+KV组合与RA+SKEW组合；

(2)KV+VAR组合诊断准确率高于RA+SKEW+KV组合但低于SKEW+KV+VAR组合；

(3)第3.1小节方法的诊断准确率最高。

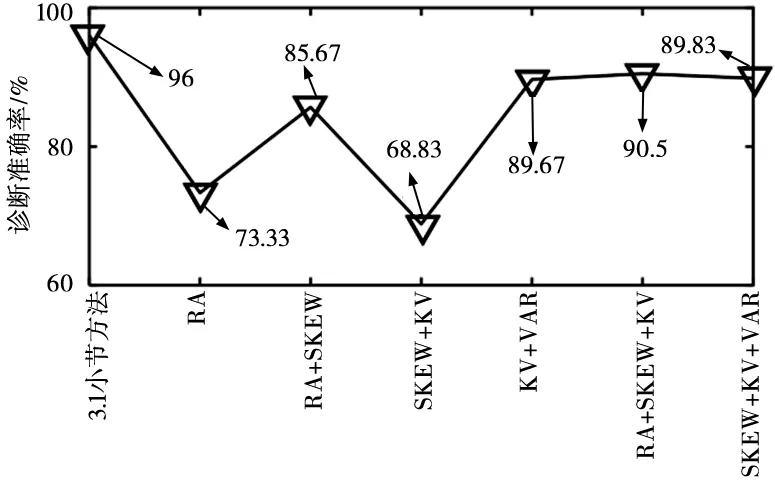
图11 第3.1小节方法与DTCWT+组合时域特征诊断准确率

上述结果表明时域特征种类数量不是越多越好，多种时域特征进行组合缺乏理论指导，穷举法计算复杂，时间成本过高；若将常见时域参数全部作为特征，则特征向量的维度会增加，部分不能体现故障特点的特征成为冗余，给后续诊断造成负担。

此外，相较于3.1小节方法明确地计算功率特征，由于暂时没有统一的选择并组合时域特征的方法，即使时域特征种类相同，诊断结果也会因前期不同的信号处理方法等情况而出现偏差，增加轴承故障诊断的不确定性。

3.4 评价指标分析

为深入分析3.1小节方法与3.2和3.3小节方法对不同特点的信号的特征提取能力。除总体识别率，即表征正确诊断信号种类的能力，再引入内圈、球体和外圈识别率，最终评价结果如表2所示。

表2 评价结果

第3.1小节方法具有最高的总体识别率，能够完美提取3种故障直径的外圈故障特征，具有优秀的提取3种故障直径的内圈故障特征的能力，提取球体故障特征的能力在4种方法中最高，但依然存在上升空间。

4 结论

本文提出了幅频对比算法优化的双树复小波变换结合自回归功率谱的滚动轴承故障诊断方法，对复杂滚动轴承故障提取功率特征，并将其作为遗传算法优化的支持向量机(GA-SVM)的输入，诊断故障类型。通过总体识别率等评价指标验证该方法能够有效区分多种混合故障并得出以下结论：

(1)双树复小波变换的二叉树结构实现对信号无间隔采样，减小因信息丢失造成的分解错误，改善频率混叠问题。

(2)幅频对比算法能够排除带有部分虚假频率和频率混叠严重的频带子信号，进一步提高DTCWT获取特征信息的准确性。

(3)自回归谱的递推思想包含频带子信号前p个时间内的信息，结合频率和功率信息，消除因为特征选择和预处理方法造成的不确定性，降低特征维度和计算成本，获得信号典型特征，具有较高的故障识别率。