杠杆型串联非线性能量阱整星隔振系统的振动控制

李东辉，李 晨，张业伟，臧 健

(1.沈阳航空航天大学 航空宇航学院，沈阳 110136；2.新乡航空工业集团有限公司，河南 新乡 453700)

众所周知，航天器对于其附加质量有严苛的技术要求，而非线性能量阱(nonlinear energy sink,NES)具有附加质量小、可靠性强、鲁棒性强、振动抑制频带宽、无需能源提供等优点[1-2]。

近年来研究人员对非线性能量阱进行了大量的研究。针对离散系统，杨凯等[3]基于非线性输出频率响应函数，对引入了非线性能量阱的单自由度振动系统进行了分析，通过分析非线性能量阱各参数对振动抑制效果的影响，对非线性能量阱进行了动力学参数设计。Boroson等[4]研究了几种并联非线性能量阱的最优设计，获得了更大的平均效率。Dai等[5]研究发现在适当的非线性能量阱参数下，可以有效抑制圆柱涡激振动。Qiu等[6]将锥形弹簧所含有的立方非线性应用到非线性能量阱中，研究发现这种弹簧不会引入新的线性刚度。Xue等[7]研究了具有非线性能量阱的线性系统的非线性行为和减振问题，发现具有非线性能量阱的线性系统在简谐和随机激励下也能实现较大的减振 。熊怀等[8]研究了耦合非线性能量阱的非保守系统的定向能量传递现象，给出了非线性能量阱具有吸振能力时线性振子阻尼的有效范围。

对于连续体系统，Zhang等[9]研究了带有非线性能量阱的轴向运动梁的热激振动抑制问题，通过数值计算结果表明，该结构可以有效抑制热激振动。刘艮等[10]研究了非线性能量阱在悬臂薄板振动抑制中的应用，发现非线性能量阱对结构响应位置较为敏感，并且在位移响应最大位置处减振效果最大。Zhang等[11]提出用非线性能量阱来抑制轴向运动梁的强迫振动，结果表明非线性能量阱与有很好的控制过度振动的潜力。

此外，非线性能量阱也被广泛应用于工程实际中，Guo等[12]用非线性能量阱抑制机翼的极限环振荡(Limit cycle oscillation,LCO)，研究了LCO抑制对气弹性系统的影响。结果表明，结构参数对超临界Hopf分岔系统和亚临界Hopf分岔系统有不同程度的影响。杨凯等[13]研究了空间结构振动抑制的被动非线性消振方法，提出了适用于空间环境的非线性消振器结构及动力学模型。Yang等[14]将非线性能量阱耦合到整星结构的卫星适配器中，分别通过数值、有限元以及试验验证了非线性能量阱对于卫星振动抑制的有效性。孙斌等[15]针对某型民用航空发动机双频带激励特点，建立了单自由度线性振子耦合非线性能量阱的动力学模型，研究发现非线性能量阱对双频带外激励有更好的振动抑制效果。Zhang等[16]提出了一种将非线性能量阱与悬浮磁电式能量采集器相结合的整星能量采集装置。该装置有效地降低了振动，具有比现有系统更强的能量采集能力。Li等[17]将非线性能量阱与压电能量采集装置结合。研究结果表明，这种集成的压电结构可以有效地降低振动，并获得一定的振动能量。

近年来，非线性能量阱的结构设计有了若干发展，Wei等[18]提出并分析了一种并联非线性能量阱的方法，研究发现并联非线性能量阱与传统非线性能量阱相比能跟有效地抑制振动。Zang等[19]提出了一种新型杠杆型非线性能量阱(lever-type nonlinear energy sink,LNES)，研究发现杠杆型非线性能量阱比传统非线性能量的吸振性能更好而且附加质量更小。钟锐等[20]对比研究了单自由度非线性能量阱和两自由度串联非线性能量阱的吸振效能，重点分析了串联NES对高分支响应的抑制作用。Zhang等[21]提出一种新型磁滞非线性能量阱 (hysteresis nonlinear energy sink,HNES)，仿真结果表明新型磁滞非线性能量阱能够有效的对主结构进行振动控制。

本文基于杠杆型非线性能量阱，应用串联非线性能量阱的方法，构成一个带有杠杆型串联非线性能量阱的整星结构。对采用串联非线性能量阱后的杠杆非线性能量阱整星系统进行振动控制研究，对杠杆型串联非线性能量阱与杠杆型并联非线性能量阱的吸振性能进行对比研究。

1 带有杠杆式串联非线性能量阱的整星结构

传统杠杆型非线性能量阱模型如图1所示，本文所研究系统模型如图2所示，质量m1、线性弹簧k1以及线性阻尼c1组成了单自由度整星结构，结构质量m1受到一个外部的谐波激励F=Acos(ωt)。杠杆式串联非线性能量阱由质量m2，m3阻尼c2，c3以及非线性刚度k2，k3组成的两个非线性能量阱串联组成，与一根忽略质量的刚性杆相连。刚性杆的A点与结构的质量相连。D点通过弹簧k2、阻尼c2与m2相连。

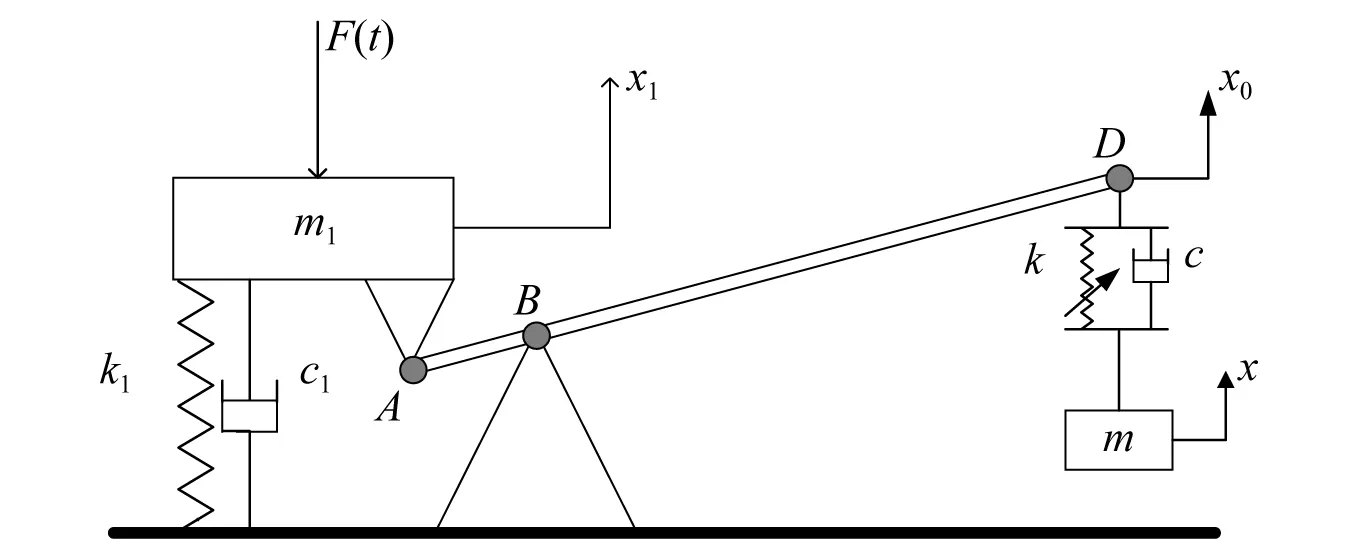
图1 带有传统杠杆式非线性能量阱的整星结构Fig.1 The system model with a traditiona llever-type nonlinear energy sink

图2 带有杠杆式串联非线性能量阱的整星结构Fig.2 The system model with lever-type nonlinear energy sinks

本文假设杠杆的运动幅值较小，因此由牛顿第二定律得到系统的动力学方程

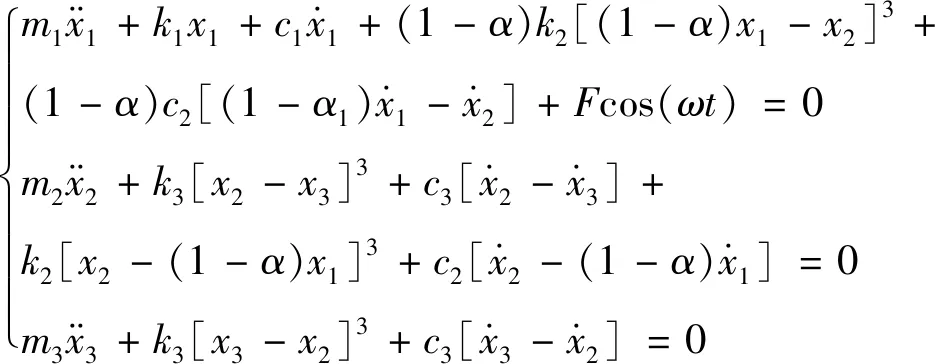
式中：xi为结构mi(i=1，2，3)的位移；x0为D点的位移；A点的位移与结构m1相同；杠杆支点位置用参数α来表示，α为长度AD与AB的比值。

无量纲参数为

(2)

把式(1)进行无量纲处理得

(3)

式中，l为线性弹簧k1在100 N作用下的伸长。

基于谐波平衡法，式(3)的振动响应可以近似为一组有限谐波的叠加。因为系统仅含立方非线性，我们设解响应为1次谐波与3次谐波的叠加。

这里aij和bij(i=1，2，3)，(j=1，2，3)为待确定的谐波系数。将式(4)代入式(3)中，平衡sin(iγτ)与cos(iγτ)(i=1，3)的系数，得到一组非线性代数方程式(5)。

通过结合伪弧长延伸法我们可以得到各阶谐波系数，进而确定幅频特性曲线。为了有效的描述带有高阶系数的幅频特性曲线，在这里我们用均方根值来处理系统的响应。

-a11cos(τγ)γ2-b11sin(τγ)γ2-9a31cos(3τγ)γ2-9b31sin(3τγ)γ2+a11cos(τγ)+b11sin(τγ)+a31cos(3τγ)+

b31sin(3τγ)+ζ1[-a11sin(τγ)γ+b11cos(τγ)γ-3a31sin(3τγ)γ+3b31cos(3τγ)γ]+

λ2[-a12cos(τγ)γ2-b12sin(τγ)γ2-9a32cos(3τγ)γ2-9b32sin(3τγ)γ2]+

λ3[-a13cos(τγ)γ2-b13sin(τγ)γ2-9a33cos(3τγ)γ2-9b33sin(3τγ)γ2]+

(5)

(6)

下面对由谐波平衡法得到的幅频响应进行数值验证，系统参数如表1所示。

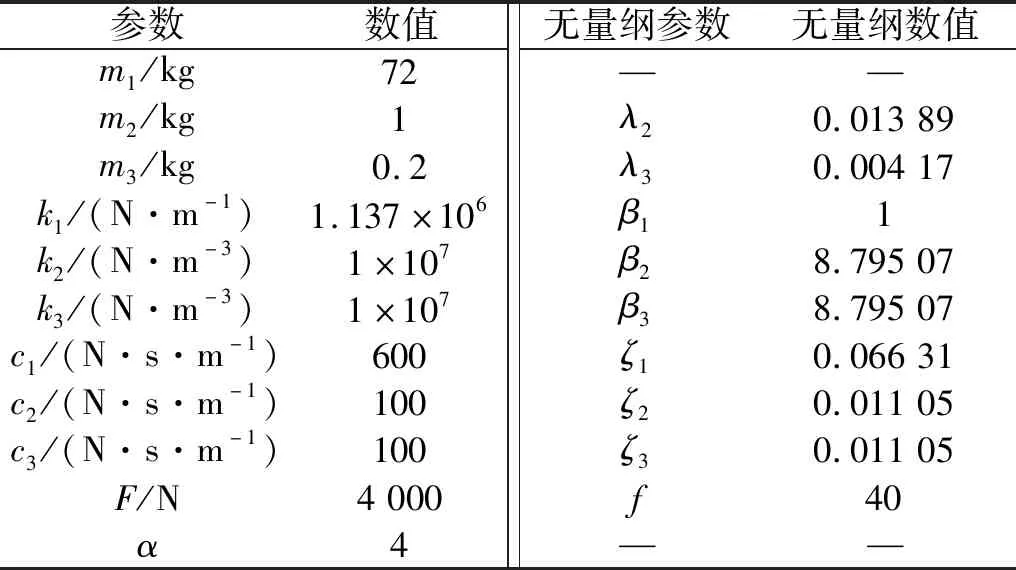
表1 系统参数Tab.1 System parameter

通过比较谐波解析解与数值解发现，总体上，三阶谐波解与数值解已经很吻合了，如图3所示。

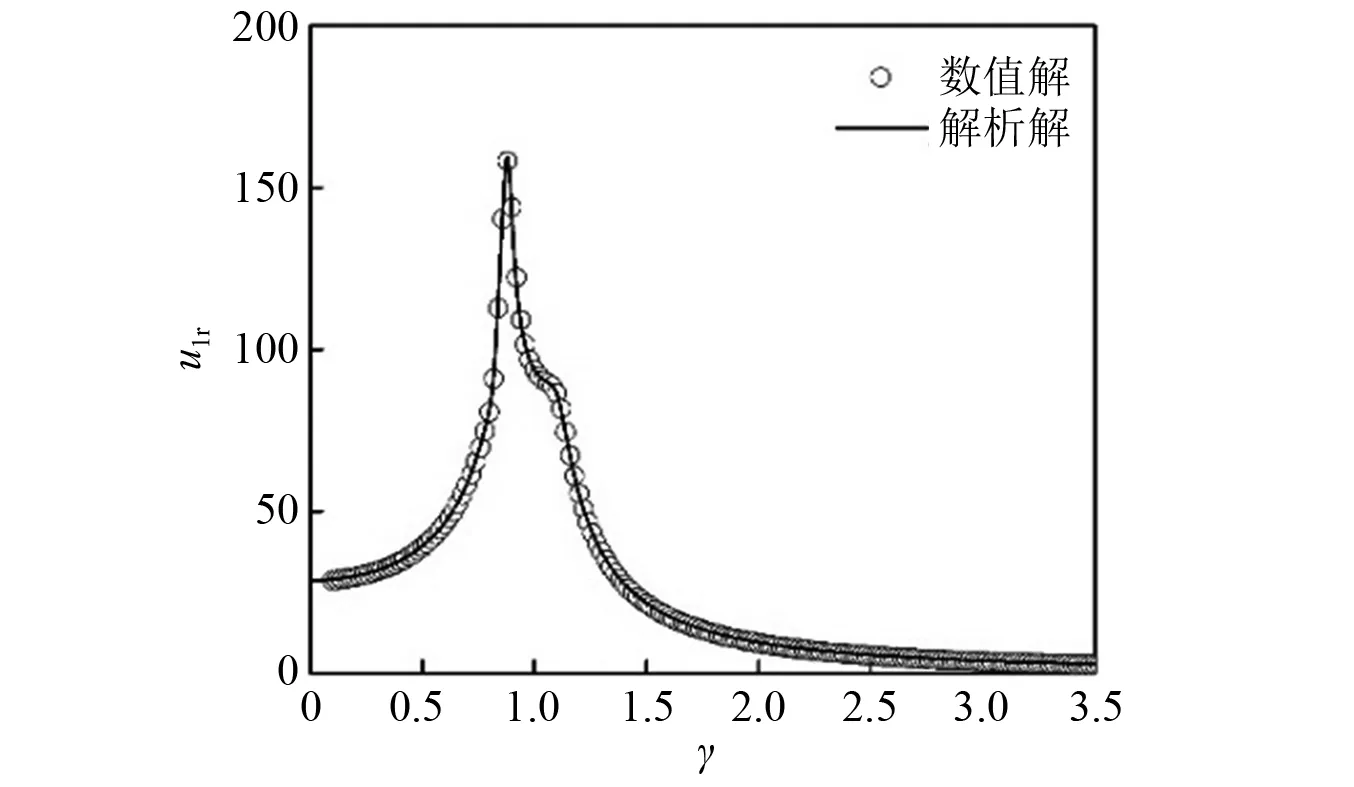
图3 系统幅频响应解析解与数值解的对比Fig.3 Comparison of the amplitude-frequency curve of the energy sink based on the analytical and numerical methods

此外，如图4所示，在不同激振频率下，系统的振动形式始终呈现稳定的周期响应，并无准周期与混沌运动。

图4 不同激励频率对系统响应的影响Fig.4 Influence of different excitation frequencies on system response

2 杠杆型串联非线性能量阱的质量、刚度以及杠杆支点位置对系统幅频响应的影响

2.1 质量对系统幅频响应的影响

下面讨论杠杆串联非线性能量阱的质量λ2和λ3对系统幅频响应的影响。首先讨论质量λ2对系统幅频响应的影响，参数设置如表1所示。质量λ2对系统幅频响应的影响如图5所示。

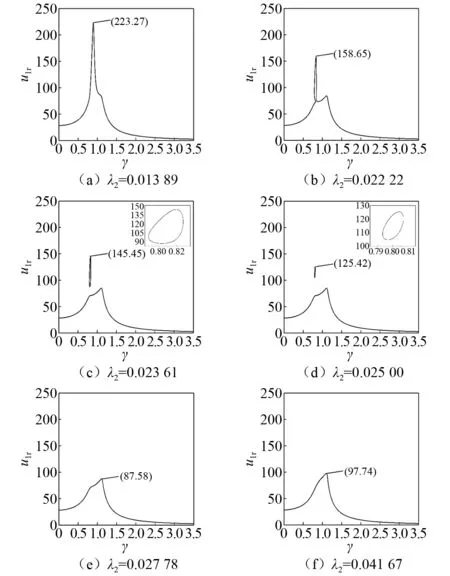
图5 质量λ2对系统幅频特性的影响Fig.5 Amplitude-frequency response curve of the structure varying mass λ2

在质量λ2较小时，随着质量λ2参数的增大，幅频响应曲线的峰值逐渐降低；继续增大质量λ2，系统的幅频响应曲线向右弯曲，弯曲频率大约在0.79～0.81；随着质量λ2的增大，在共振频率附近出现孤立的环状共振响应；伴随着质量λ2的增大，孤立的环状共振响应逐渐远离系统原本的幅频响应曲线，并逐渐减小直至消失。孤立环状响应的出现会使系统幅频响应曲线的峰值极大的增加，为避免孤立环状响应的出现，需要进一步优化参数设置。

将初始参数λ3=0.002 78改为λ3=0.004 17。质量λ2对系统幅频响应的影响如图6所示。从图6中可以看出，在质量λ2参数较小时，随着质量λ2的增大，幅频响应曲线的峰值逐渐降低。当质量λ2=0.020 83变为质量λ2=0.027 78时，幅频响应曲线的峰值由86.10增至89.52，继续增大质量λ2，幅频响应曲线的峰值又开始逐渐增大。图6与图5相比，没有出现孤立的环状共振响应。

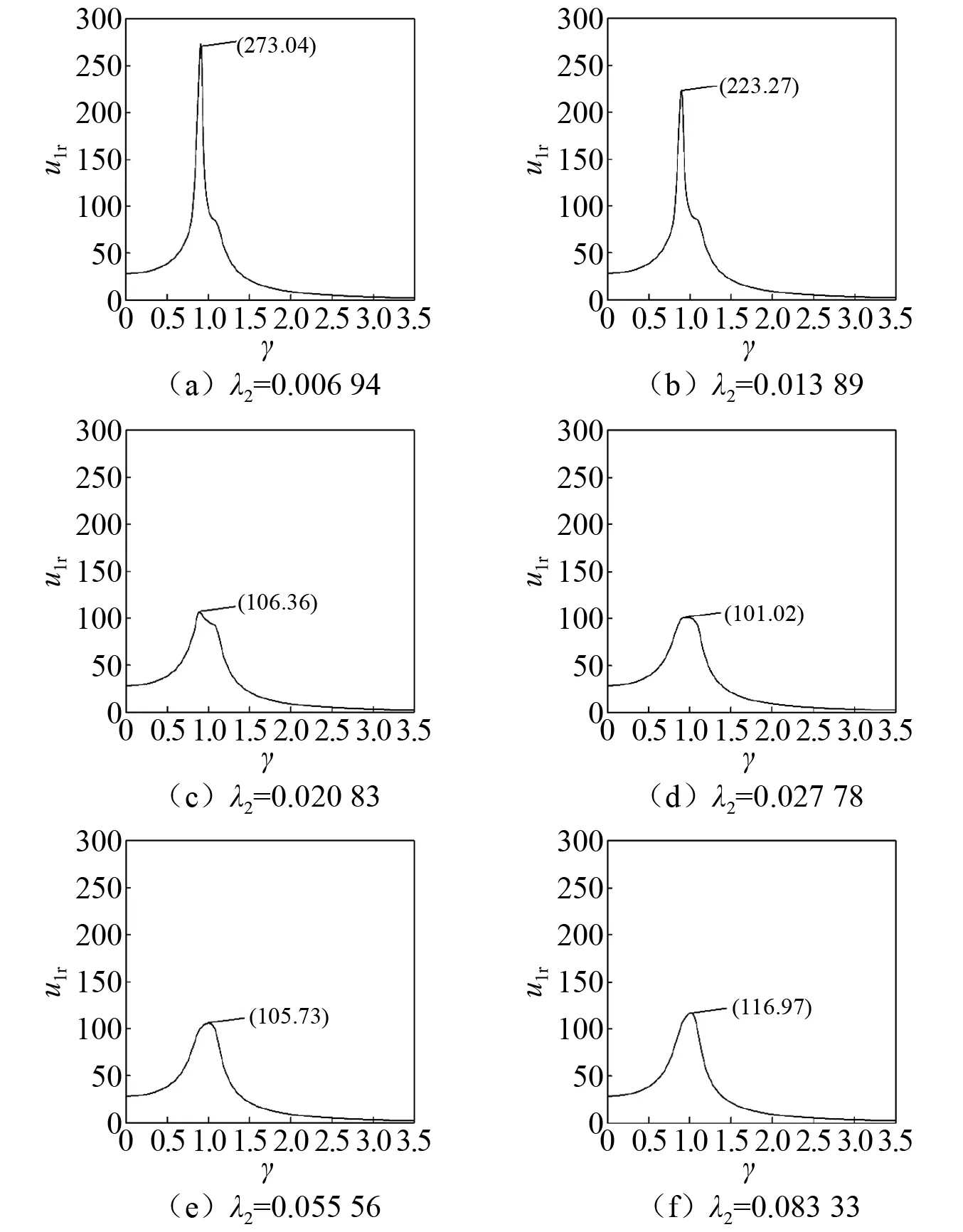
图6 质量λ2对系统幅频特性的影响Fig.6 Amplitude-frequency response curve of the structure varying mass λ2

综上我们可以得出，适当质量的λ2可以有效降低系统的振幅。合适的质量λ3选择，可以避免孤立的环状共振响应的出现。

图7展示了质量λ3对系统幅频响应的影响。

从图7中我们可以看出，在质量λ3较小时，随着质量的增大，幅频响应曲线的峰值逐渐降低，当质量λ3=0.006 94变为λ3=0.008 33时，幅频响应曲线的峰值由101.02上升到105.73，继续增大λ3的质量，幅频响应曲线的峰值开始逐渐上升。综上，一个适当质量的λ3可以有效降低系统的振幅。

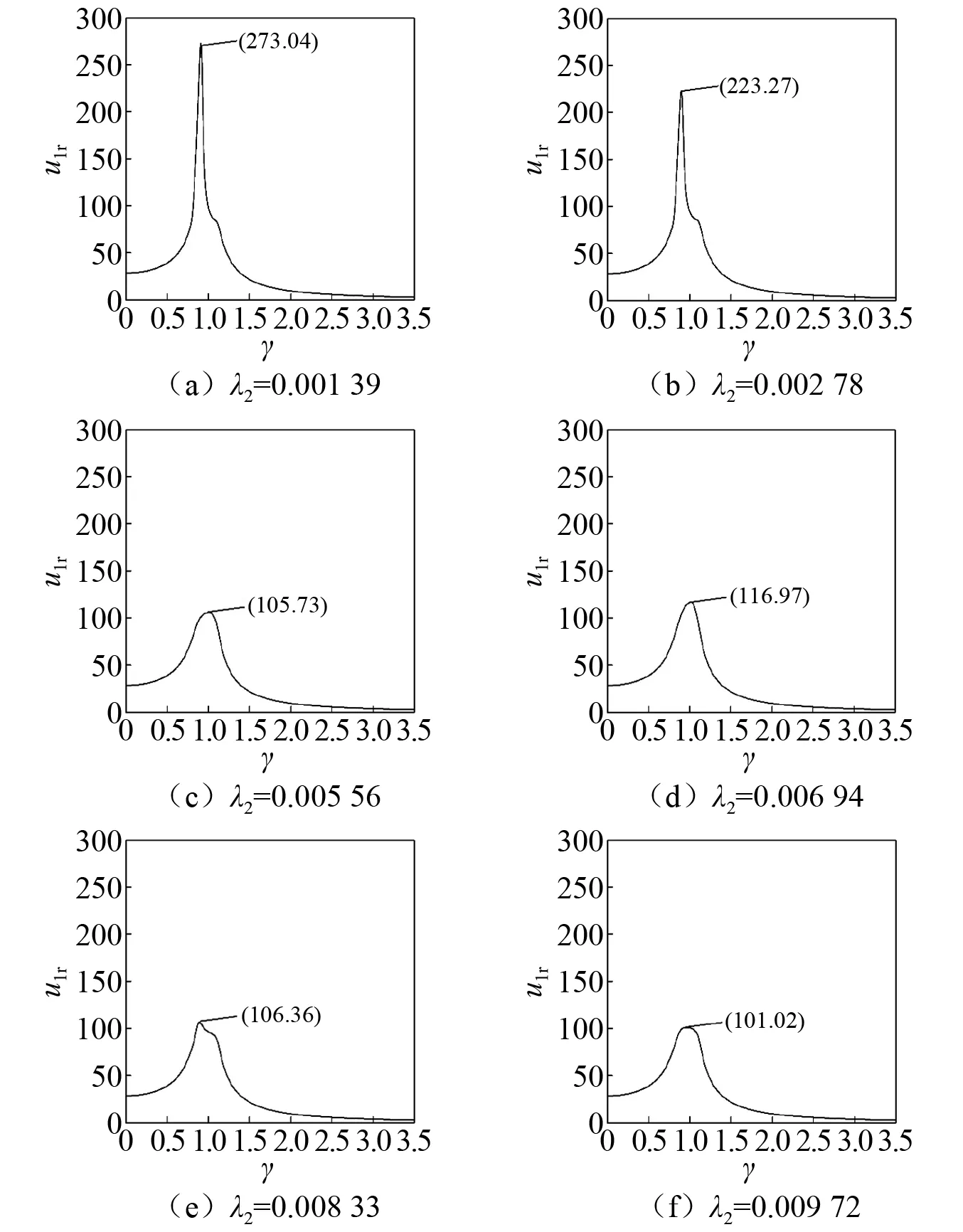
图7 质量λ3对系统幅频响应的影响Fig.7 Amplitude-frequency response curve of the structure varying mass λ3

2.2 非线性刚度对系统幅频响应的影响

下面讨论杠杆型并联非线性能量阱的非线性刚度β2和β3对系统幅频响应的影响。图8展示了非线性刚度β3对系统幅频响应的影响。从图8中可以看出，伴随着非线性刚度β3的增大，系统幅频响应曲线的峰值逐渐降低，这种下降的趋势一直保持到大约在β3=6.156 6时停止；继续增大非线性刚度β3，系统幅频响应曲线的峰值逐渐上升。综上，适当的非线性刚度β3可以小幅降低系统的振幅。

图8 刚度β3对系统幅频响应的影响Fig.8 Amplitude-frequency response curve of the structure varying nonlinear stiffness β3

图9展示了非线性刚度β2对系统幅频响应的影响。从图9中可以看出，在非线性刚度β2较小时，随着β2参数的增大系统幅频响应的峰值逐渐降低；当非线性刚度β2达到大约6.156 55时，下降的趋势开始停止。接着伴随着非线性刚度β2的增大，系统幅频响应曲线的峰值逐渐上升。综上，适当的非线性刚度β2可以有效降低系统的振幅。

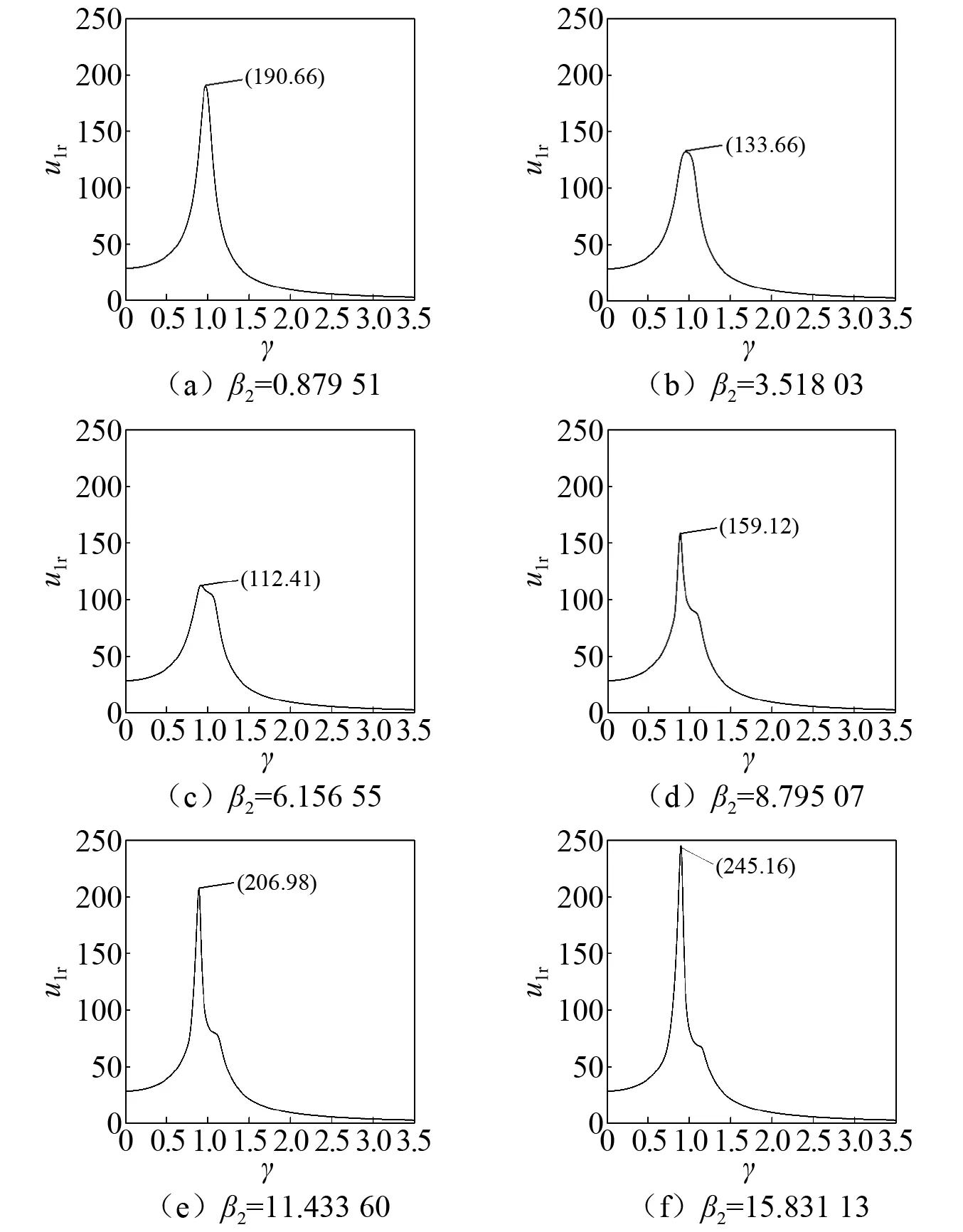
图9 刚度β2对系统幅频响应的影响Fig.9 Amplitude-frequency response curve of the structure varying nonlinear stiffness β2

2.3 支点位置α对系统幅频响应的影响

下面讨论杠杆型并联非线性能量阱的支点位置α对系统幅频响应的影响。图10展示了支点位置α对系统幅频响应的影响。从图10中可以看出，在α较小时，随着α的增大，系统幅频响应的峰值逐渐降低。当α大约为7时，下降的趋势开始停止，接着增大α，系统幅频响应曲线的峰值开始上升。综上，适当的杠杆支点位置可以有效降低系统的振幅。

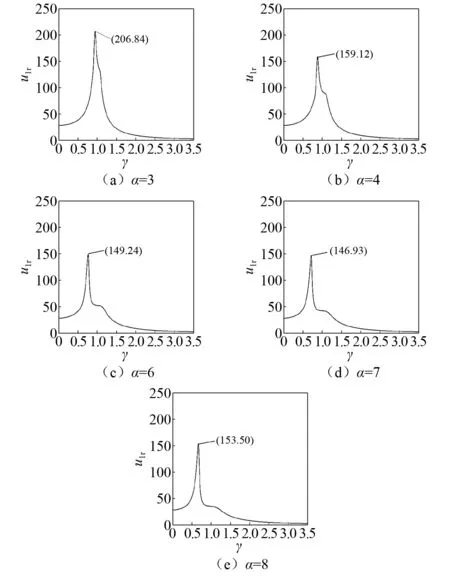
图10 支点位置α对系统幅频响应的影响Fig.10 Amplitude-frequency response curve of the structure varying fulcrum α

3 杠杆型串联非线性能量阱与杠杆型并联非线性能量阱性能的比较

下面我们对杠杆型串联非线性能量阱与杠杆型并联非线性能量阱的吸振性能进行系统比较，将幅频响应曲线的峰值以及总体附加质量作为评价非线性能量阱吸振性能的指标。为了便于比较，我们将整星结构分别耦合杠杆型并联非线性能量阱以及杠杆型串联非线性能量阱。图11为带有杠杆式并联非线性能量阱的整星结构。

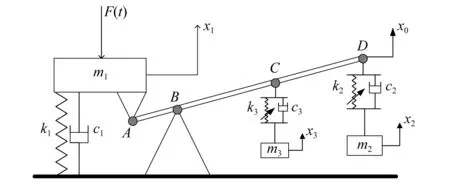
图11 带有杠杆式并联非线性能量阱的整星结构Fig.11 The system model with a lever-type parallel nonlinear energy sink

为保证总体附加质量相同，在调节参数过程中保持λ2=0.013 89不变，通过调节λ3来对比研究并联非线性能量阱与串联非线性能量阱的吸振性能。

如图12所示，当λ3=0.001 39时，串联非线性能量阱与并联非线性能量阱系统幅频响应的峰值分别是273.04和312.78。当λ3=0.002 78时，串联非线性能量阱与并联非线性能量阱系统幅频响应的峰值分别是223.27和309.62。当λ3=0.006 94时，串联非线性能量阱与并联非线性能量阱系统幅频响应的峰值分别是101.02和299.51。当λ3=0.008 33时，串联非线性能量阱与并联非线性能量阱系统幅频响应的峰值分别是105.73和292.41。在总体附加质量参数较小时，串联非线性能量阱系统幅频响应曲线的峰值是低于并联非线性能量阱的。随着总体附加质量参数的增加，两个系统的幅频响应曲线的峰值都开始降低，串联系统下降的幅度要远大于并联系统下降的幅度。继续增大总体附加质量参数，串联系统幅频响应曲线的峰值开始上升，并联系统幅频响应曲线的峰值仍远大于串联系统。这说明，杠杆型串联非线性能量阱的吸振性能是要优于杠杆型并联非线性能量阱的。

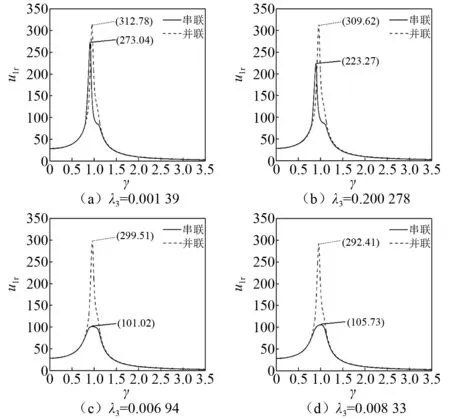
图12 杠杆型并联非线性能量阱与杠杆型单个非线性能量阱吸振性能比较Fig.12 Comparison of vibration absorption performance of the lever-type series NES and the lever-type parallel NES

4 结 论

本文研究了谐波激励下带有杠杆型串联非线性能量阱结构的整星系统的振动控制。基于谐波平衡法结合弧长延伸法确定了系统的幅频响应。通过调节该结构的质量、非线性刚度以及支点位置等参数，对结构的整星振动控制能力进行了系统的分析与评价。最后，对比分析了杠杆型串联非线性能量阱与杠杆型并联非线性能量阱的吸振能力。具体结论如下：

(1)杠杆型串联非线性能量阱结构可以有效的对整星系统进行振动控制。

(2) 在杠杆型串联非线性能量阱下方串联的质量较小时，系统的幅频响应曲线会出现孤立的环状共振响应，导致系统幅频响应曲线的峰值增大。特别指出，串联适当的质量可以避免孤立环状响应的出现。

(3)随着杠杆型串联非线性能量阱的质量、非线性刚度和支点位置参数的逐渐增大，系统的幅频响应曲线的共振峰会逐渐降低至最小值然后再逐渐增大。

(4) 在总体附加质量相同的情况下，杠杆型串联非线性能量阱的吸振性能要优于杠杆型并联非线性能量阱。