海底盾构隧道结构端部效应及抗减震措施研究

赵 凯，卢艺静，王彦臻，李兆焱，陈国兴

(1.中国地震局 工程力学研究所 地震工程与工程振动重点实验室,哈尔滨 150080;2.南京工业大学 岩土工程研究所,南京 210009)

海底盾构隧道受潮汐、水流、波浪等气象水文环境影响小，建成后连续运载能力强，已成为跨海通道建设的首选方案，确保其地震安全性至关重要。小泉淳[1]通过盾构隧道震害调查发现，竖井(如始发竖井、中间竖井和接收竖井)与隧道连接处极易发生破坏，如1985年墨西哥米却肯地震和1995年日本兵库县南部地震中均出现了盾构隧道-竖井节点的地震损坏，而在1989年洛马普塔地震中，某盾构隧道因在与通风竖井连接处安装了柔性接头，而未发现任何震害现象。盾构隧道-竖井节点特殊的几何构型和概念特征使得盾构隧道端部的地震行为和性能与常规隧道段存在很大差异。禹海涛等[2]利用振动台试验研究盾构隧道-竖井连接部位地震响应特征，分析了地震动特性对环间张开量、加速度和径向应变的影响，发现连接部位竖井与管环之间质量和刚度的差异会加剧结构震损，须对连接部位进行特殊抗震设计。因此，开展盾构隧道-竖井节点的地震性能及其抗减震措施研究具有重要的理论意义和工程价值。

竖井的设置以及管环纵向接头地震性能的差异导致盾构隧道结构的刚度沿轴线分布不均匀，显著影响海底盾构隧道的纵向地震反应特性[3-7]。目前，海底长大隧道纵向地震响应分析方法主要有基于位移的简化分析方法，如纵向等效连续化模型和纵向梁-弹簧模型[8]。Anastasopoulos等[9]采用梁-弹簧模型研究了深埋海底隧道的非线性地震反应。刘天添等[10]基于Winkler 地基模型，推导出了地震作用下海底盾构隧道与地基之间的动力相互作用系数以及隧道结构位移表达式，初步研究了高水压对海底盾构隧道地震响应的影响。何川等考虑盾构隧道环间接头的状态非线性力学行为，建立了迭代广义反应位移法，研究了盾构隧道纵向非连续、非线性的纵向地震反应特性。Chen等[11-12]基于广义反应位移法，考虑隧道纵向管环间的螺栓连接，建立了某海底长大盾构隧道纵向梁-弹簧模型，重点研究了强震作用下管环间的张开量。然而，地下结构的地震性能与其几何形状和刚度分布密切相关，盾构隧道在竖井部位的刚度突变会使隧道结构受到差异位移的作用，形成复杂的空间效应。隧道结构的端部约束效应使得弹性地基梁模型的建立存在困难，无法确定端部边界条件。王建宁等[13]通过对土-盾构隧道动力相互作用振动台试验的模拟，研究了隧道结构的端部约束效应。杨林德等[14-16]均开展地铁车站接头的振动台试验和数值模拟，研究了地铁车站结构的端部效应，得出车站结构端部效应的范围，指出区间隧道的存在削弱了车站结构前后端墙的整体抗震性能。然而，海底盾构隧道-竖井节点的地震行为和性能与地铁地下车站接头结构明显不同，在强地震作用下，海底盾构隧道端部存在复杂的上覆海水-海床土体-地下结构体系的动力相互作用效应。目前隧道-竖井节点对于海底盾构隧道产生的端部效应及其抗减震措施，国内外学者却鲜有研究。

针对海底隧道中关键部位进行局部三维精细化模型的地震反应分析，可以考虑复杂的土层分布几何构型，采用适当的动力学本构模型描述海床土体和结构的非线性性能，以及土-结构接触面的性能[17-21]，能够深入全面地揭示海底隧道中关键部位在地震反应中的受力和变形过程及其特点。楼梦麟等指出海底隧道建模过程中需重点关注：①模型范围大小的问题；②上覆海水动水作用的模拟；③时域分析中阻尼矩阵的合理建模及其影响；④地震输入方式的选择与影响等。鉴于此，本文以汕头市苏埃海底隧道工程为研究背景，考虑海床土体的动力非线性特性、盾构隧道管环间纵向螺栓连接以及盾构隧道-竖井柔性接头等因素，建立了盾构隧道-竖井连接区段三维精细化有限元模型，探讨了地震波、盾构隧道-竖井节点结构抗减震措施等因素对盾构隧道结构端部效应的影响，研究结果可为海底盾构隧道-竖井节点的结构抗震设计提供参考依据。

1 工程背景

苏埃海底隧道工程位处汕头市中心城区海湾大桥与礐石大桥之间，联接汕头南北两岸，是国内首条位于Ⅷ度地震烈度区的特长超大直径海底盾构隧道。苏埃海底隧道场址区域内地质构造多变，多条东北向、西北向断裂交织，靠近地震活动强烈的台湾海峡，未来可能遭遇的地震影响将主要来自于海洋区域。近场区域内，距工程场址约54 km处发生过2次7级以上强震；历史上，工程场址多次遭遇地震烈度达Ⅴ～Ⅷ度地震，其中，有3次地震对工程场址的影响烈度达到Ⅷ度。隧道场址区域历史地震及断裂分布如图1所示。海底隧道始发井位于南岸围堰中，盾构隧道单管外径14.5 m，内径13.3 m。苏埃海底盾构隧道竖井长 50 m，宽25 m，埋深30 m，结构外壁厚1.2 m。明挖隧道段截面尺寸近似为40 m×20 m，外壁厚1.3 m。

图1 苏埃海底隧道区域地震构造图Fig.1 Regional tectonic setting and historical earthquake data of the Suai subsea tunnel site

据工程勘察报告，盾构隧道-竖井节点区域水域宽约3.5 km，水深3.0～13.5 m，海底标高一般在-3～-7 m。海床从上到下主要为淤泥、淤泥质土、中粗砂、粉质黏土和花岗岩，各土层厚度依次约18 m，7 m，2 m，8 m和7 m。钻孔土层的剪切波速和P波波速沿深度的分布图和各类土模量比G/Gmax、阻尼比λ与剪应变幅值γ的关系曲线分别如图2、图3所示。

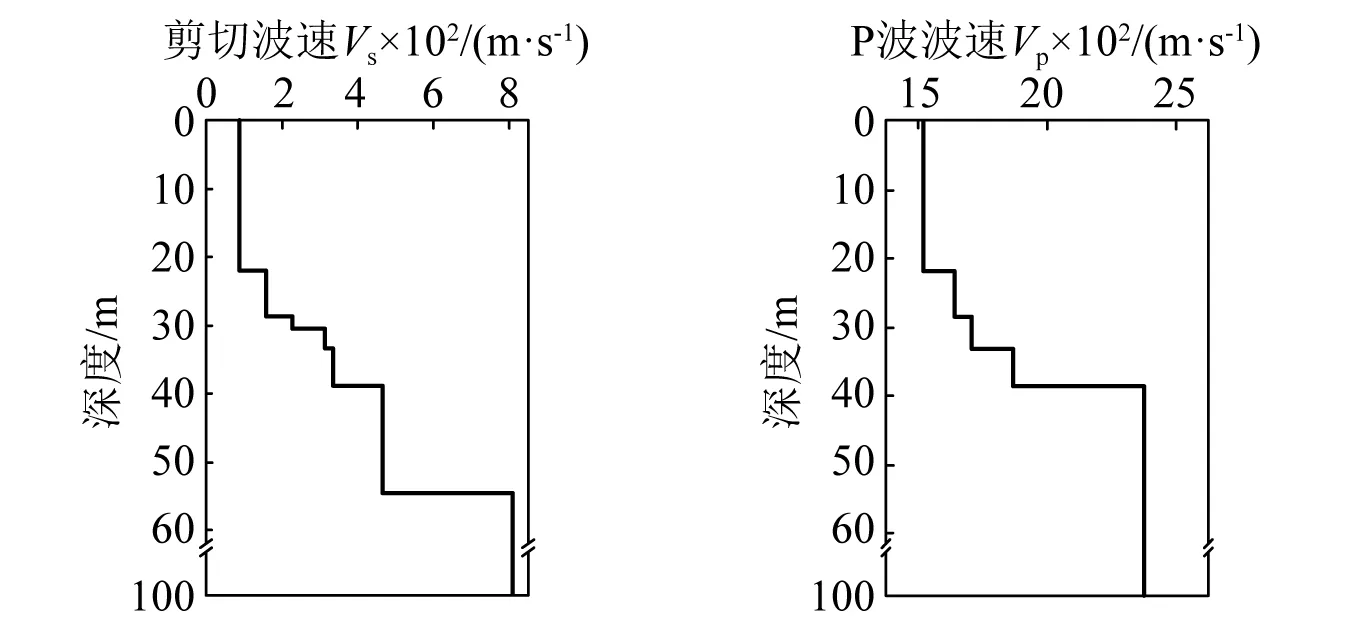
图2 典型钻孔S波和P波波速剖面图Fig.2 Typical S and P wave velocity profiles

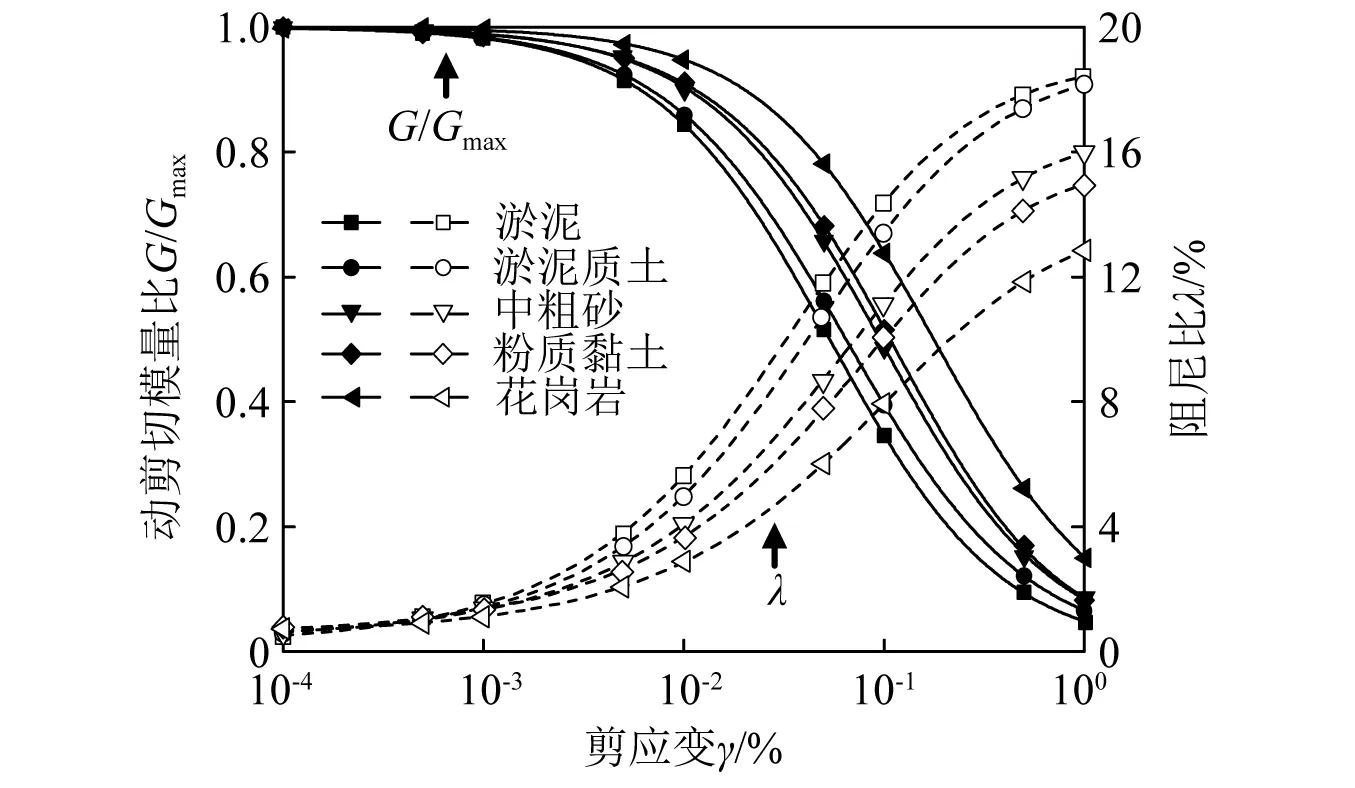
图3 海底隧道场址典型土的G/Gmax-γ和λ-γ试验曲线Fig.3 The G/Gmax-γ and λ-γ curves of typical soils for the subsea tunnel site

2 三维精细化有限元模型

2.1 模型建立

通过ABAQUS有限元分析软件[22]建立苏埃海底隧道工程盾构隧道-竖井连接区段三维精细化有限元模型，如图4所示，将竖井节点处明挖段隧道与盾构隧道均沿隧道轴线向两侧延伸100 m，其中盾构隧道环宽2 m，共50环，模型纵向取225 m，宽度取180 m，取剪切波速不小于500 m/s处且其下不存在更低波速界面作为基岩面，模型计算深度取至100 m。采用拉格朗日实体单元C3D8R模拟结构和土体，结构和土体之间定义接触面，法向采用硬接触，切向摩擦因数取0.3[23]；采用理想流体Us-Up状态方程和欧拉单元EC3D8R描述海水的动力特性：密度ρ=1 000 kg/m3，水中声速V=1 483 m/s，黏性系数η=0.001 kg/(m·s)。利用耦合欧拉-拉格朗日(coupled-euler-lagrange，CEL)技术模拟海水与海床界面的流固耦合作用，即满足法向速度连续和应力连续，且界面切向应力为零条件[24-25]。在模型海床四周和底部边界设置黏弹性人工边界条件，模型海水四周边界设置无反射边界条件。

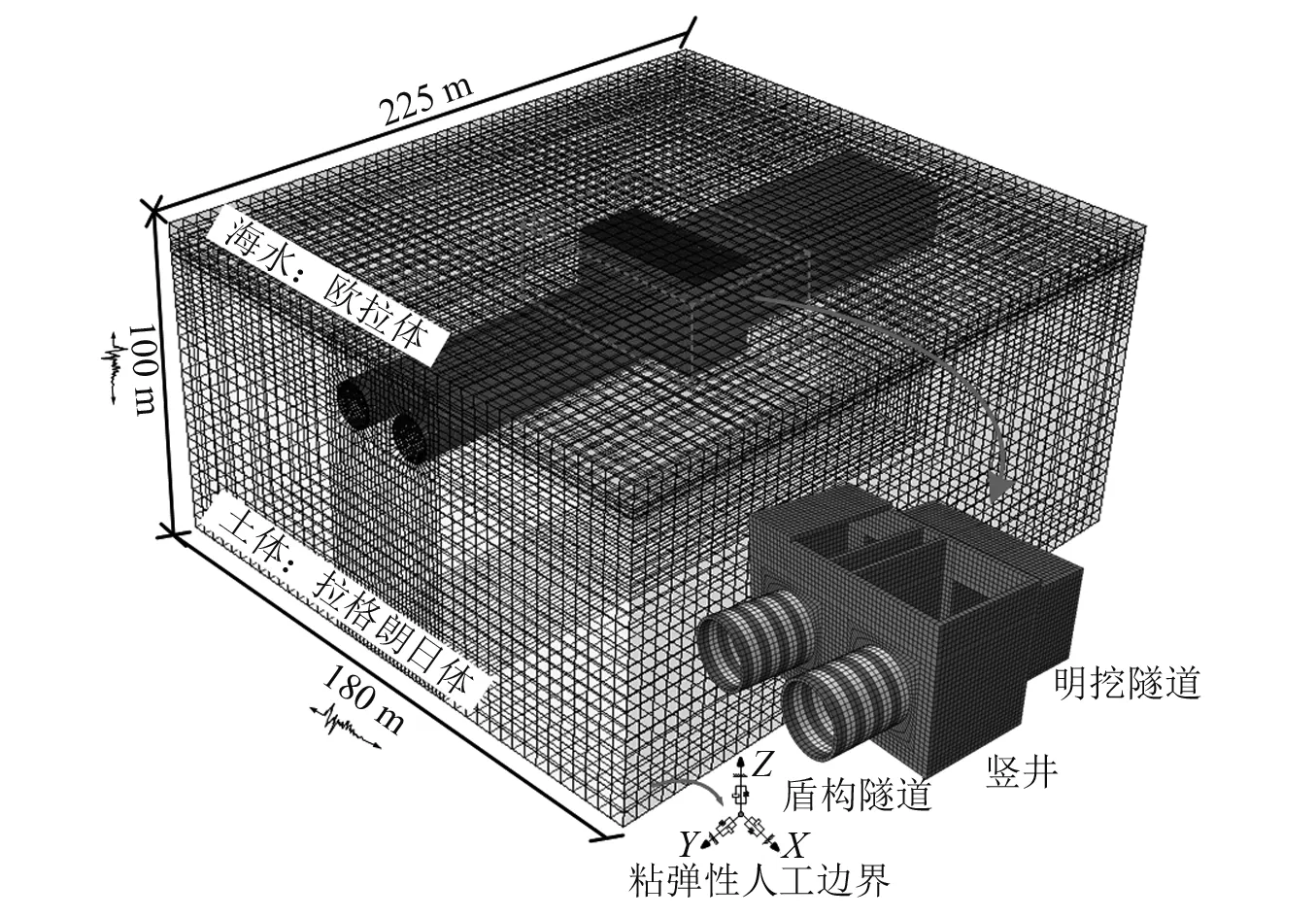
图4 海底盾构隧道-竖井连接部位三维精细化有限元模型Fig.4 3D refined finite element model of the junction between the subsea shaft and the shield tunnel

2.2 材料本构模型及参数

对于海床土体采用总应力法分析，选用陈国兴等[26-27]考虑三维应力空间中不规则加卸载的Non-Masing法则构造的Davidenkov本构模型(DCZ模型)描述海床土体的动力非线性和滞回性，如图5所示。

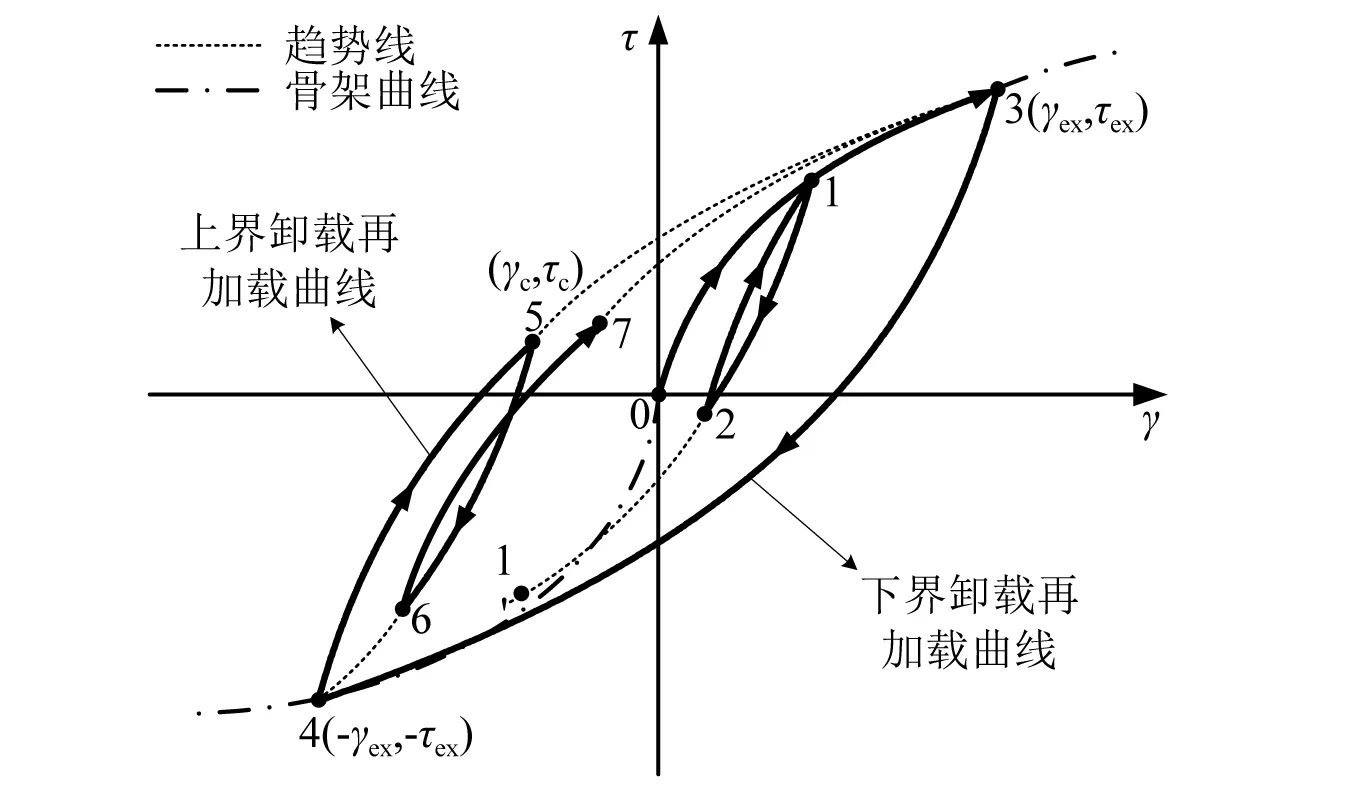
图5 DCZ模型描述的应力-应变关系曲线示意图Fig.5 Stress-strain curves of the DCZ model under irregular loading-unloading-reloading

(1) 初始骨架曲线的表达式为

τ=Gγ=Gmaxγ[1-H(γ)]

(1)

其中，

(2)

(2) 应变反转后，应力-应变路径将沿式(3)定义的滞回曲线前行，并指向记录到的应变最值点。

(3)

其中，

(4)

(5)

(3) 当滞回曲线与骨架曲线重叠时，后续应变路径将沿骨架曲线移动至下一个应变反转点。

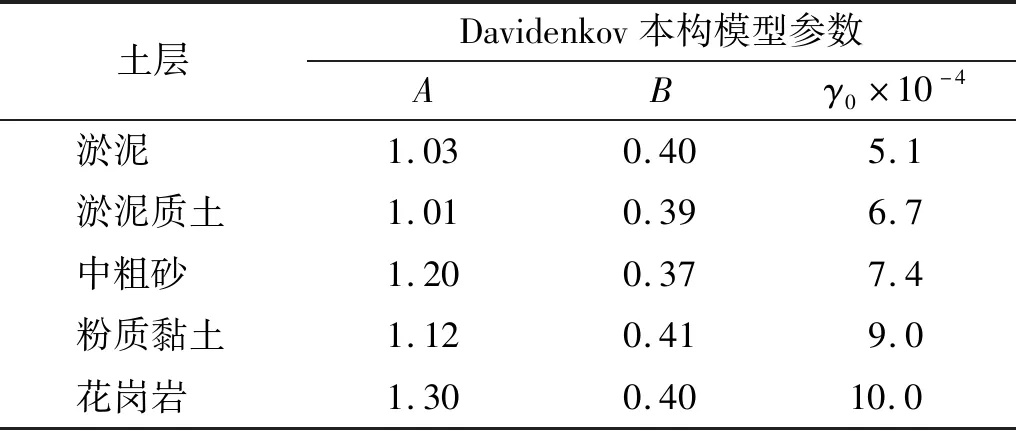
表1 场地土本构模型参数Tab.1 Values of the constitutive parameters for the soils

采用Lubliner等[28]提出的黏塑性动力损伤模型模拟循环荷载作用下混凝土塑性损伤过程和刚度变化。

混凝土强度等级为C60，模型参数如表2所示。

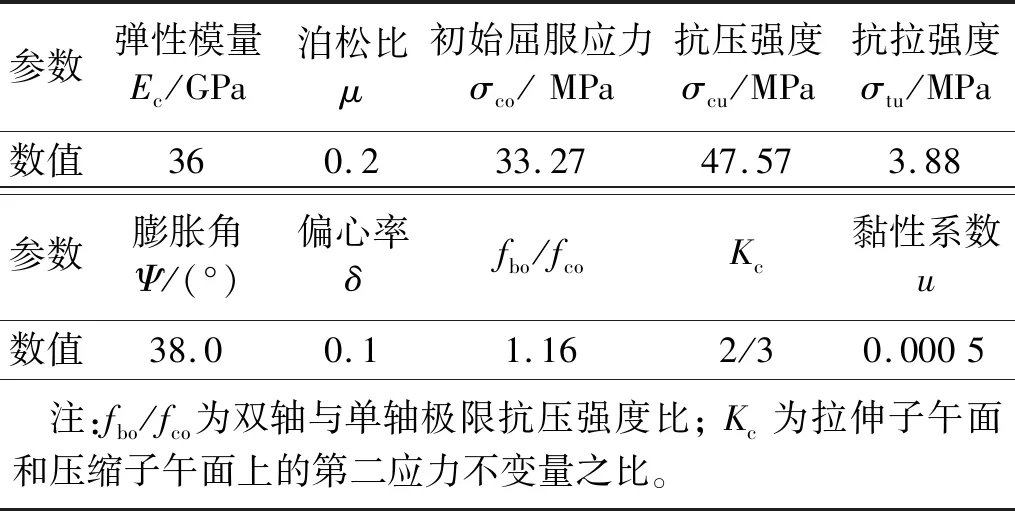
表2 混凝土材料模型参数Tab.2 Model parameters of the concrete material

2.3 盾构管片接头模拟

“管片环+接头”非连续结构形式导致盾构隧道纵向变形行为具有状态非线性特征，本文仅考虑管环之间的纵向连接缝，基于等效连续化模型忽略管片之间的环向连接缝。管片纵向接头由环缝面及连接螺栓构成。假定环缝面受拉区由连接螺栓承担全部拉力，受压区由管片混凝土承担全部压力，暂不考虑螺栓预紧力作用。如图6所示，在管环间设置接触面模拟环缝面及连接螺栓的状态非线性行为，在受压区采用法向硬接触，在受拉区采用黏结模型。依据相邻管环在单向拉伸状态下，相同张开量所受合力相同的原则，将纵向螺栓刚度等效为沿管环圆周连续均匀分布。随环缝张开量的发展，连接螺栓将达到屈服，环缝接头刚度也将衰减。因此，黏结模型的刚度衰减采用应力控制标准，即法向拉应力达到相应限值时刚度开始衰减

图6 相邻管环受力变形特征及其力学描述Fig.6 Deformation characteristics and the relation between the internal forces and deformations between adjacent pipe rings

(6)

(7)

式中：δy为弹性极限变形；δu为极限位移；fy为螺栓屈服应力；fm为螺栓极限应力；l0为螺栓长度；Eb为螺栓弹性模量；α为弹塑性刚度比。螺栓物理力学指标及黏结模型参数参考陈国兴等的研究。相邻管环间设置42根M42型螺栓，张开量允许限值为15 mm。

参照文献[29]，在竖井端墙和盾构隧道端部增设实体连接单元(C3D8R)，纵向宽度取0.2 m。柔性连接环与端墙和盾构隧道均采用节点耦合连接(即节点自由度相一致)，与围岩的接触设置与盾构隧道一致，即结构与土体间增设接触面，法向采用硬接触，切向摩擦因数取0.3。通过降低单元的弹性模量来模拟盾构隧道-竖井柔性接头，如图7所示。

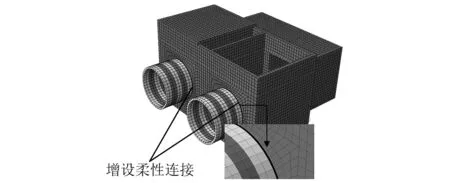
图7 盾构隧道-竖井柔性接头模拟Fig.7 Simulation of the shield tunnel-shaft flexible joint

2.4 输入地震动

由于缺乏工程场址及附近地区强震记录，依据区域地震活动背景，选取震级、震中距与场址邻近区域历史强震相近的国外强震露头基岩记录，选用2008年日本Iwate Ms 7.2级地震IWATE27台站和2010年新西Darfield Ms 7.1级地震Pages Road Pumping台站两组加速度记录作为苏埃海底隧道的基岩输入地震动，地震记录详细信息如表3所示。图8为Darfield记录和Iwate记录加速度时程曲线及傅氏谱。其中：Darfield记录低频成分发育；Iwate记录的中高频成分丰富。将水平向峰值加速度PGA分别调整为0.1g，0.2g和0.4g，对应抗震设计中50年超越概率63%(小震)、10%(中震)和2%(大震)。水平向与竖向PGA比值取为1∶0.65。

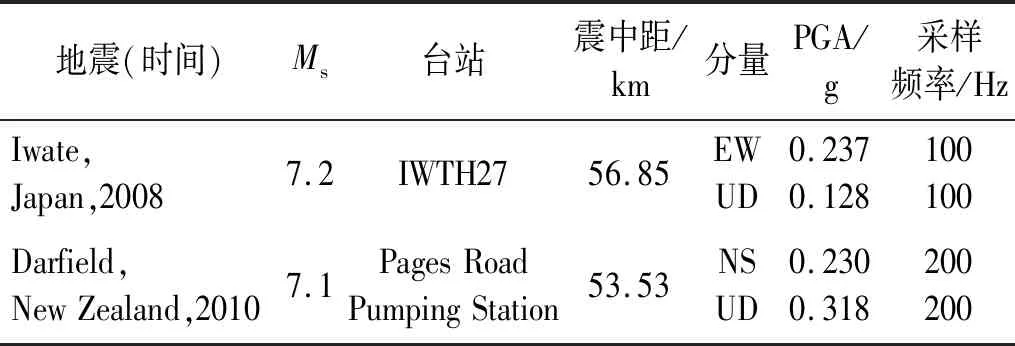
表3 地震记录详细信息Tab.3 Details of ground motion records

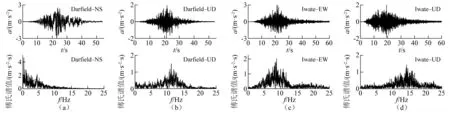
图8 基岩输入地震动加速度时程及其傅氏谱Fig.8 Acceleration time histories and Fourier spectra of the input bedrock motions

2.5 计算工况

为了探究地震波、盾构隧道-竖井节点结构抗减震措施等因素对盾构隧道结构端部效应的影响，确定如表4所示计算工况。已有研究表明：调整螺栓数量和提高螺栓等级可以有效提高海底盾构隧道的纵向抗震性能。如Chen等、谢宏明等[30]分别将苏埃海底盾构隧道环间连接螺栓数量由42根提高至58根和56根，宋仪[31]将管片纵向螺栓由56根M42/6.8级加强为56根M42/8.8级来抵抗地层突变处隧道结构的差异位移作用和地震应力集中。基于此，通过进一步增加盾构隧道-竖井连接环的螺栓数量至64根、82根来提高接头的抗震性能。

表4 计算工况汇总Tab.4 Summary of calculation cases

3 结果与分析

盾构隧道-竖井连接部位是抗震薄弱环节，结构震损、管片环间变形过大会导致严重后果。考虑模型对称性，以B隧道为监测对象，定义图9中盾构隧道与竖井连接环为节点管片环，取如图所示8个监测位置(分别为拱顶、外拱肩、外拱腰、外拱脚、拱底、内拱脚、内拱腰和内拱肩)进行分析。峰值环缝张开量为两个相邻管环位移时程的最大差值的绝对值。

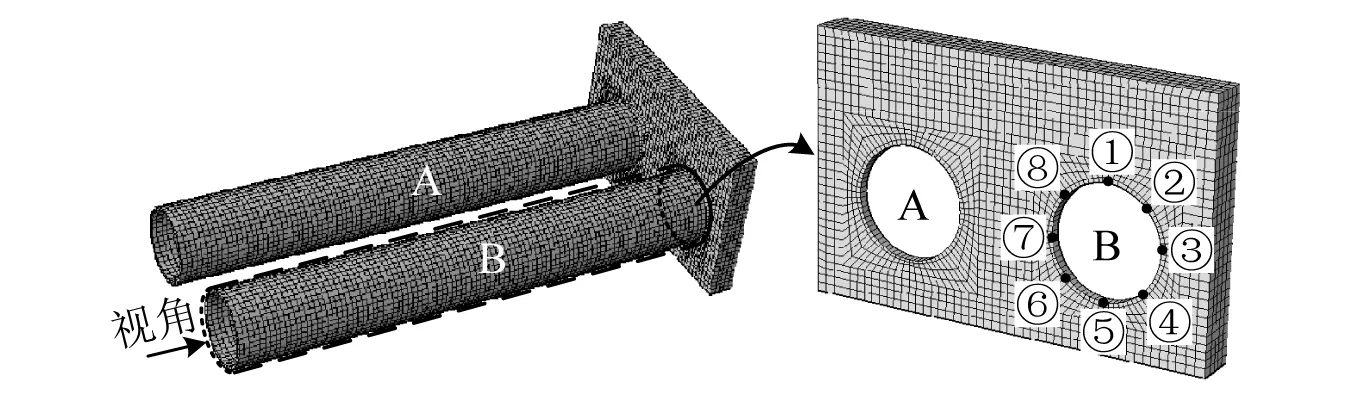
图9 隧道-竖井接头处的监测位置Fig.9 Monitoring positions at the tunnel-shaft junction

参照王建宁等的研究，以远离竖井端墙的隧道截面响应R作为基准值(距竖井端墙80 m)，规定当地震响应比值Ri/R=[0.9,1.1]时可认为该区域不受竖井端墙的影响，其中，Ri为分析隧道截面的响应量，如加速度、层间位移、能量和弯矩。

3.1 盾构隧道结构端部效应

图10给出了输入Darfield波和Iwate波时管片峰值环缝张开量沿隧道轴线分布情况。各工况下，盾构隧道-竖井节点环缝张开量约为常规隧道段的2～5倍，端部效应影响范围约为1.5D(D为隧道直径)，这与陈国兴等研究中振动台试验结论相一致。峰值环缝张开量分布曲线沿隧道轴线方向由陡峭至平缓，即远离竖井端墙盾构隧道端部效应迅速衰减。在0.4gDarfield波作用下距竖井端墙4 m范围内峰值环缝张开量已超出防水限值，应采取相应抗减震措施。

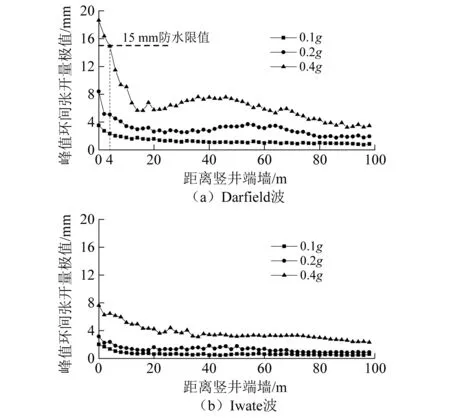
图10 峰值环缝张开量沿隧道轴线方向分布Fig.10 Longitudinal distribution of maximum values of opening widths at the ring segment

图11给出了盾构隧道-竖井节点峰值环缝张开量沿横截面分布情况。由图11可见，各工况下最大峰值环缝张开量位于管环顶部和拱肩处，而管环底部的峰值环缝张开量最小。图12为盾构隧道-竖井节点管环拱肩处环缝张开量的时程曲线。从图12中可以看出，地震作用下管环间反复出现张开和闭合现象，且环缝张开量数值始终为正，这表明管片混凝土未出现受压破碎而相互侵入的现象。随着输入地震动强度增加，各监测点峰值环缝张开量呈非线性增加，在 Darfield 波作用下，峰值环缝张开量的最大相对增量百分比由小震-中震时的109%增至中震-大震时的142%；在Iwate波作用下，峰值环缝张开量的最大相对增量百分比由118%增至163%；说明在强震激励下，螺栓刚度衰退，非线性变形显著。输入0.1g和0.2gDarfield波时，横截面各监测点环缝张开量均满足防水要求；输入0.4gDarfield波时，外拱肩峰值环缝张开量超过15 mm。在0.1g，0.2g和0.4gIwate波作用下，各测点环缝张开量均在防水限值内。综上可以发现：隧道结构端部效应随地震动强度的增大而呈非线性增大趋势，低频发育的Darfield波作用比中高频发育的Iwate波作用时引起更大的管环张开量，这与土体非线性和结构特性密切相关。然而，盾构隧道端部效应影响范围与竖井-盾构节点自身结构特性相关，受地震波类型及幅值影响较小。

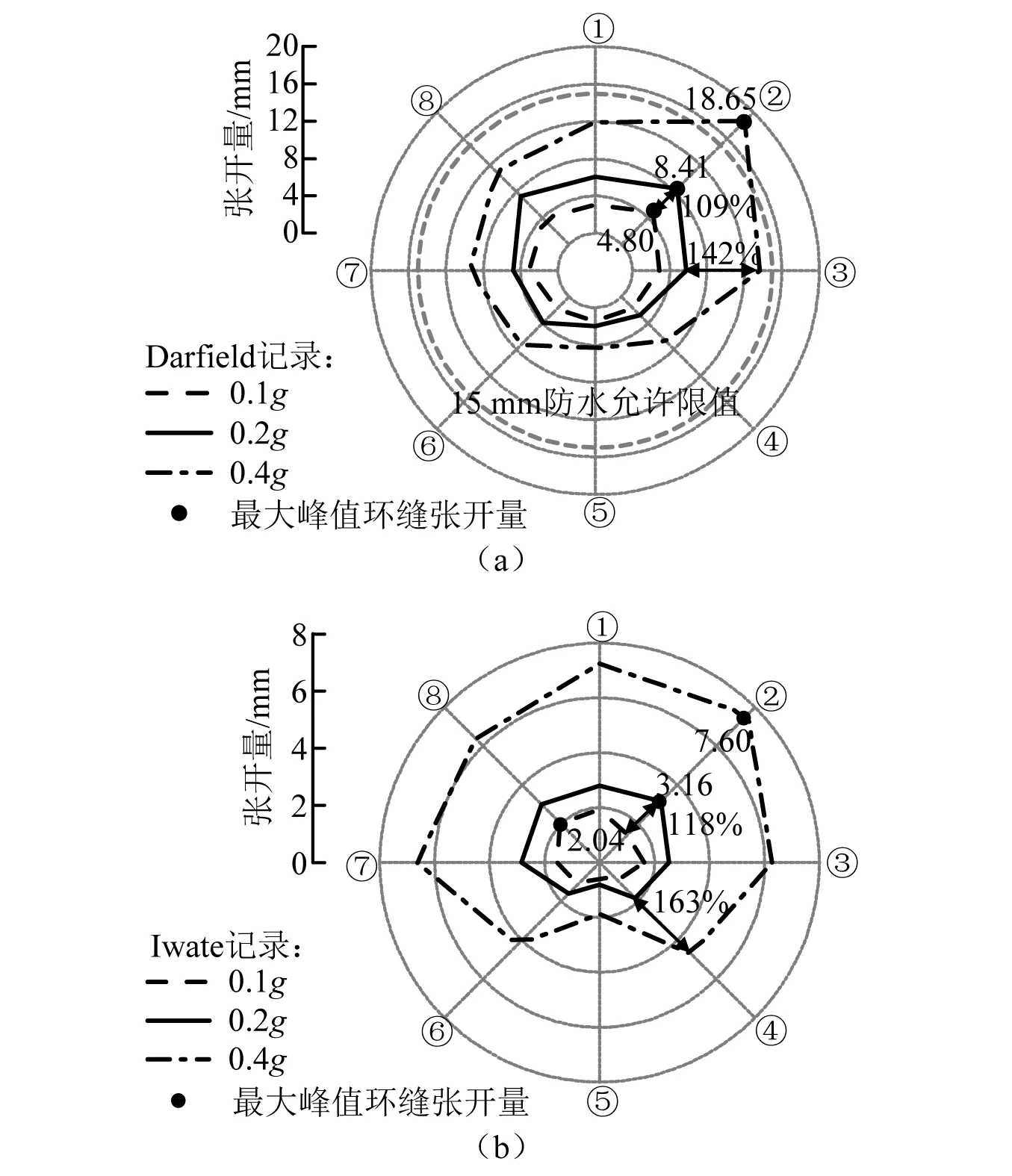
图11 隧道-竖井接头各测点峰值张开量Fig.11 Peak opening widths of monitoring elements at the joint of tunnel-shaft junction

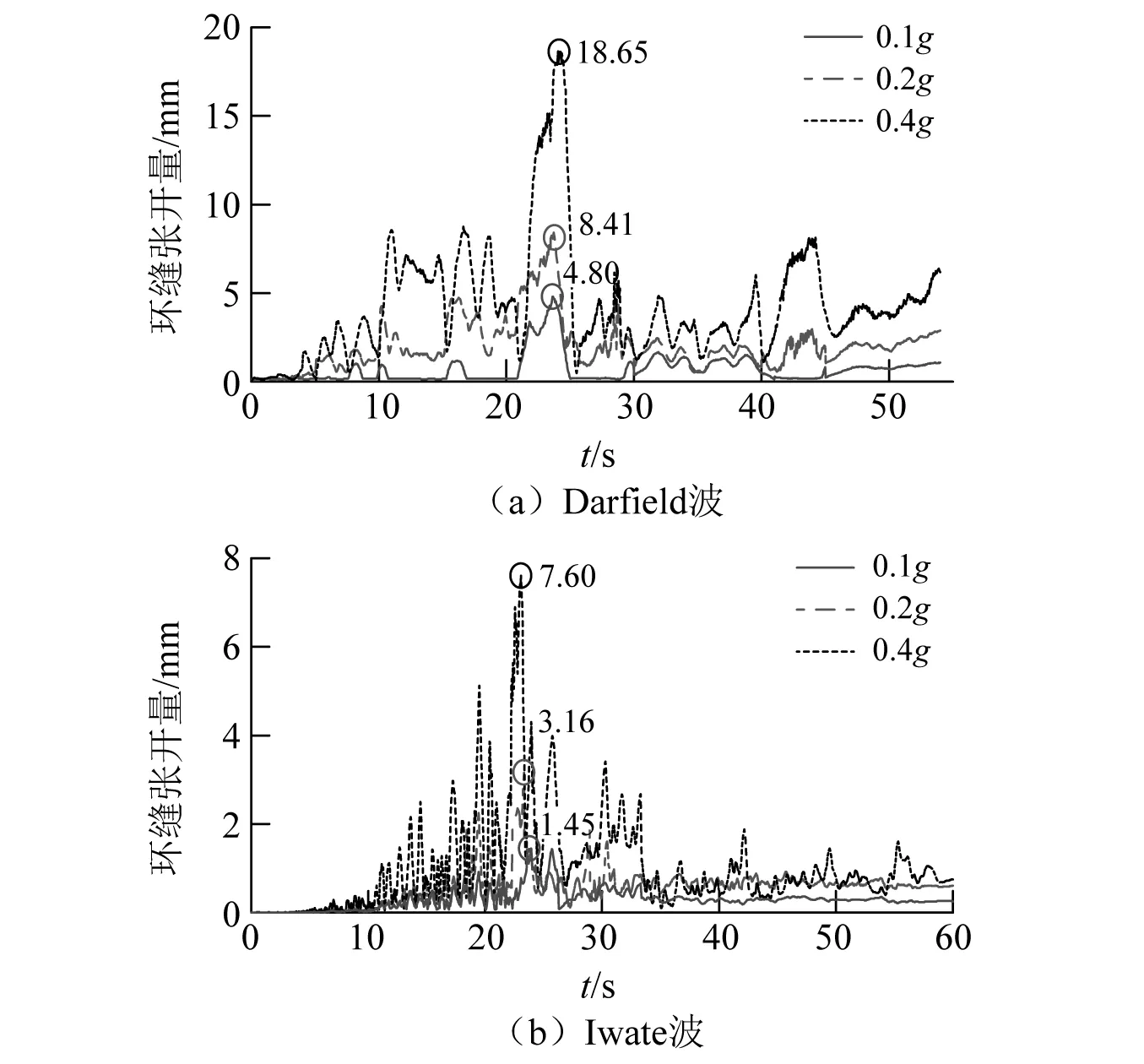
图12 隧道-竖井接头外拱肩处环缝张开量时程Fig.12 Time-histories of opening widths at the spandrel of the joint of tunnel-shaft junction

3.2 盾构隧道-竖井节点抗减震措施分析

3.2.1 峰值环缝张开量

图13为输入0.4gDarfield波时采用不同减隔震措施下峰值环缝张开量沿纵向分布情况。由图13可见，增加盾构隧道-竖井节点环缝连接螺栓数量可以有效降低盾构隧道端部环缝张开量，节点管片环峰值环缝张开量均小于15 mm，距竖井端墙约20 m范围内峰值环缝张开量显著减小，说明通过增加连接螺栓数量可以改善盾构隧道-竖井连接部位的刚度突变，优化盾构隧道纵向刚度分布。增设盾构隧道-竖井柔性连接时，在柔性接头处出现明显的变形集中，峰值环缝张开量急剧增大。柔性接头的消能减震特性，可将地震波传播引起的结构变形诱导至预设的柔性接头上，降低了盾构隧道端部整体的峰值环缝张开量。

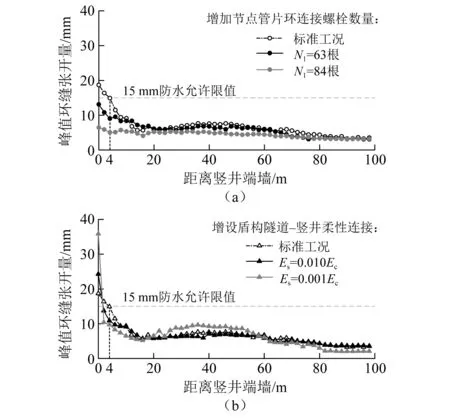
图13 不同抗震措施下环间张开量极值沿纵向分布Fig.13 Longitudinal distribution of maximum values of opening widths at the ring intersegment under different seismic measures

图14 给出输入0.4gDarfield波时不同抗减震措施下，节点管片环最大环缝张开量沿横截面分布情况。图14中可以看出：增加盾构隧道-竖井节点环缝连接螺栓数量可显著降低节点管片环各监测点峰值环缝张开量并将其控制在防水限值内。当Nl=63根时，峰值环缝张开量降至标准工况时(Nl=42根)的70.3 %；当Nl=84根时，峰值环缝张开量降至标准工况时的34.5%。增设盾构隧道-竖井柔性连接时，当Es=0.010Ec和0.001Ec时，节点管片环各监测点峰值环缝张开量大幅度提高，分别为标准工况时的130.7%和182.7%。由于外激励为两向剪切输入，外拱肩处峰值环缝张开量急剧增大，分别达到防水限值的1.63倍和2.27倍，且多个监测位置的峰值环缝张开量超过防水限值。因此，降低盾构隧道端部整体的峰值环缝张开量的同时牺牲的是柔性接头处抗震安全性，柔性接头成为结构抗震薄弱部位，应能满足预期的地震变形要求。

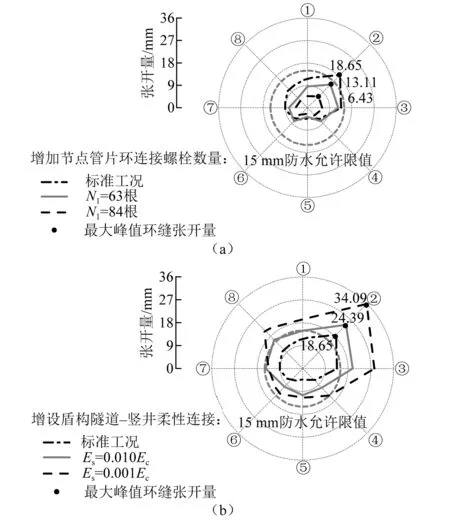
图14 不同抗震措施下隧道-竖井接头各测点峰值张开量Fig.14 Peak opening widths of monitoring elements at the joint of tunnel-shaft junction under different seismic measures

3.2.2 结构地震损伤

图15给出输入0.4gDarfield波时不同减隔震措施下盾构隧道-竖井损伤云图，损伤指数可评价混凝土结构的地震损伤程度，数值介于0(白色：无损伤状态)和1(深灰色：完全损伤状态)之间。由图15可知，提高盾构隧道-竖井接头刚度，即增加节点管片环连接螺栓数量后，放大了竖井端墙和盾构隧道端部的地震作用和损伤程度，如当Nl=84时，靠近竖井端墙的4～5管环混凝土出现贯穿性损伤。增设盾构隧道-竖井柔性接头时端墙和盾构隧道的损伤范围及程度均明显减小，说明柔性连接可以有效改善竖井和盾构隧道连接部位由刚度突变引起的结构差异位移和应力集中。然而各工况下，竖井端墙地震损伤程度均较严重，盾构隧道的存在削弱了竖井端墙整体抗震性能，是抗震设计需重点关注的部位。

图15 不同抗震措施下连接部位结构损伤云图Fig.15 Distribution cloud diagram of the damage index from the junction under different seismic measures

3.2.3 峰值地震应力分布

图16给出了盾构隧道-竖井节点管片环峰值地震应力(Mises应力)沿横截面分布情况。如图16所示，隧道拱肩、拱脚处应力集中明显，显著大于其他部位。结合图11、图14可见，峰值地震应力的分布与峰值环缝张开量分布规律相符，二者存在强相关性，较好地佐证了本文模型能有效模拟连接螺栓空间变形特征。

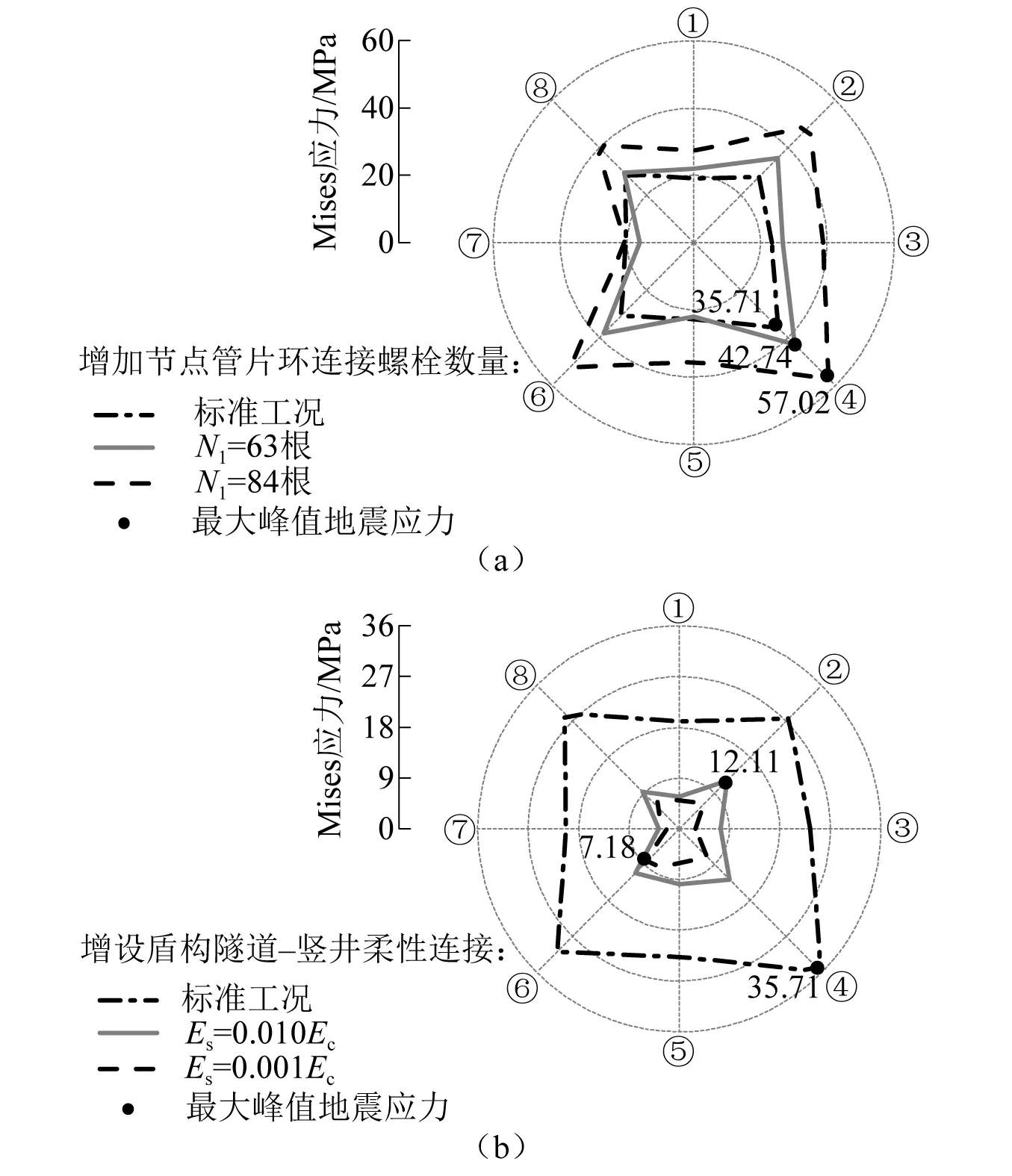
图16 不同抗震措施下隧道-竖井接头各测点峰值地震应力Fig.16 Peak Mises stress of monitoring elements at the joint of tunnel-shaft junction under different seismic measures

图16中，增加节点管环连接螺栓数量使盾构隧道-竖井结构刚度提高，节点管片环峰值地震应力明显增大。当螺栓数量增加至63根和84根时，峰值地震应力最大增幅分别为28.7%和77.1%。增设盾构隧道-竖井柔性接头能有效减小结构的地震应力和应力集中，当柔性接头模量折减至0.010Ec和0.001Ec时，峰值地震应力的最大降幅分别为81.0%和89.3%。

4 结 论

针对盾构隧道-竖井连接部位，本文以苏埃海底隧道工程为背景，考虑海床土体的动力非线性、盾构隧道环间纵向螺栓连接以及盾构隧道-竖井柔性接头等因素，建立了隧道-竖井连接区段三维精细化有限元模型，探究地震波、隧道-竖井接头抗减震措施等因素对隧道结构端部效应的影响，主要结论如下：

(1) 地震作用下盾构隧道具有明显的端部效应，隧道-竖井节点环缝张开量约为常规段的2～5倍，影响范围约为1.5D(D为盾构隧道直径)，环缝张开量峰值沿隧道横截面分布不均匀，最大峰值环缝张开量位于管环顶部和拱肩，而管环底部的张开量最小。盾构隧道的存在削弱了竖井端墙的整体抗震性能。

(2) 隧道结构端部效应随地震动强度增大呈非线性增大趋势，低频发育的Darfield波比中高频发育的Iwate波引起更大的管环张开量，在0.4gDarfield波作用下距竖井4 m范围内张开量极值超限，应采取相应抗震措施。隧道端部效应影响范围与隧道-竖井自身结构特性相关，受地震波类型及幅值影响较小。

(3) 增加盾构隧道-竖井节点环缝连接螺栓数量可以提高结构整体抗弯刚度，有效降低盾构隧道端部环缝张开量，然而增加结构刚度会增大地震作用，导致隧道端部产生显著的应力集中，加剧了竖井端墙和盾构隧道的结构地震损伤范围及程度。

(4) 增设盾构隧道-竖井柔性连接可将地震波传播引起的结构变形诱导至预设的柔性接头上，从而降低隧道结构整体张开量，减轻了隧道端部的地震损伤范围及程度。然而，盾构隧道地震应力减小的同时牺牲的是柔性接头处抗震安全性，柔性接头成为结构抗震薄弱部位，设计应能满足预期的地震变形要求。

需注意的是，增加环间连接螺栓数量属于传统抗震措施，通过增加隧道-竖井节点的整体刚度抵抗地震作用，由于增加结构刚度会放大地震作用，增加构件尺寸和材料强度不仅导致工程造价大幅提高，且由于地震作用的不确定性难以达到预期效果。增设柔性接头通过调整隧道-竖井连接部位结构动力特性，达到消能减震作用，同时结合减震控制技术(如形状记忆合金SMA)可实现隧道-竖井节点震后可恢复性。