基于HB-AFT方法的水电机组转子-轴承系统振动特性研究

张雷克，原 倩，王雪妮，马震岳，唐华林，张金剑

(1.太原理工大学 水利科学与工程学院，太原 030024；2.大连理工大学 建设工程学部 水利工程学院，辽宁 大连 116023)

大型旋转机械是典型的机电耦合系统，在机械和电磁共同作用下转子-轴承结构在运行过程中呈现出复杂的动力学特性。鉴于异常振动对旋转机械的巨大危害，近几十年来，国内外众多学者[1-15]对其开展了广泛而深入的研究，同时取得了丰硕的研究成果。

由于研究对象受多样外激励及系统自身特点形成的运动微分方呈强非线性，利用数值计算或解析计算进行相关研究是常见且普遍的方式。以小参数摄动法、平均法、多尺度法等为代表的解析方法是获取系统周期解的一种手段，该方法求解效率高，可以直接获得系统的稳态响应。然而受小参数条件、可积条件、级数展开条件等限制[16]，其应用局限性较为明显，特别对于具有强非线性特性的微分方程，通常无法得到预期结果。数值方法虽具有精度高、收敛速度快、稳定性强等特点，不过需要指出的是，该方法对初值的依赖性强，无法准确得到系统的非稳态周期解。此外，对于系统失稳位置的附近区域来说，该方法的计算时间较为冗长。四阶Runge-Kutta法是一种典型的数值积分方法，该方法涉及到对时间项的差分或者微分，属于时域方法。HB-AFT为时域与频域相结合方法，因此，HB-AFT方法的求解效率高于四阶Runge-Kutta法，且该方法可直接求得系统周期解的近似表达式。

鉴于数值方法和解析法在求解非线性方程周期解时存在的诸多不便以及业内对转子-轴承系统振动故障诊断要求的日益提升，自20世纪80年代伊始，如何采取更为高效、准确的研究方法来开展相关分析便逐渐进入广大研究者的视野。

Yamauchi[17]于1983年首次提出了一种半解析半数值的隐式谐波平衡法(harmonic balance method with alternating frequency/time domain technique,HB-AFT)。该方法是从经典谐波平衡(harmonic balance,HB)法发展而来，能以三角级数的形式给出周期解。在求解系统周期响应过程中将响应和非线性函数同时设置为谐波解形式，根据系统离散时频特性建立谐波系数之间的关系，进而避免复杂非线性项的级数展开、积分处理等近似过程。随后，一些学者[18-20]对HB-AFT方法进行了完善，并将其逐渐应用于转子-轴承系统的准周期响应求解。Zhang等[21]考虑轴承径向间隙、轴承时变刚度和赫兹接触力等非线性因素建立了变柔度振动下的球轴承-转子系统动力学模型，通过HB-AFT方法研究了系统的周期响应，并尝试对所求周期响应进行Floquet稳定性分析，据此提出了一套周期响应求解及其稳定性分析的快速计算方法。Hou等[22]研究了转子系统在不平衡和不对中共同作用下的非线性动力学响应特性，考虑了滚动轴承的非线性支承力，将HB-AFT 方法与Floquet理论相结合，提出了一种简单的确定单自由度矩阵的策略，并给出了周期解失稳的分析方法。李洪亮等[23]考虑球轴承非线性支承力和联轴器不对中的影响，建立了含套齿联轴器的偏盘转子系统动力学模型，针对考虑非线性支承恢复力和联轴器不对中影响下的带机械套齿联轴器偏盘转子系统的动力学模型，采用HB-AFT方法求得系统的周期解，同样结合Floquet理论分析了系统运行的稳定性，并与数值积分结果进行了对比验证。

由上述介绍可知，半数值半解析时频域转换方法对于求解非线性系统微分方程具有较强的适用性，该方法已成功在时滞网络拥塞控制模型、压电机械系统及球轴承-不对中等模型中陆续得到了应用[24-28]，其在求解周期解时的准确性、高效性等特点也得到了充分的体现。然而，到目前为止国内外鲜有HB-AFT方法在水轮发电机组振动故障诊断方面的报道。

水轮发电机组是水电站核心运转设备，其转子-轴承系统在运行过程中受质量偏心力、不平衡磁拉力、油膜力等机电荷载作用不可避免产生振动，据此所建立的系统运动微分方程具有强非线性。如何从理论与数值两方面有效获取该系统周期解并洞悉其存在规律，从而掌握机组振动的内在机理具有重要的科学意义。

鉴于此，本文以水轮发电机组转子-轴承系统为研究对象，通过建立机组轴系动力学模型，采用HB-AFT方法对系统进行求解，并与数值计算方法得到的结果进行对比，验证了该方法对水轮发电机组振动研究的适用性。同时，以轴颈间隙为控制参数对有无不平衡磁拉力作用下机组的动态响应进行了讨论。

1 水轮发电机组转子-轴承系统模型

图1是在固定直角坐标系O-xyz中所建的转子-轴承系统模型。图1中：O为定子内圆中心；S为轴颈初始中心，当O与S重合时，模型处于静止状态；G为转子的重心；e0=SG为转子的质量偏心；e=OS为大轴旋转偏心。

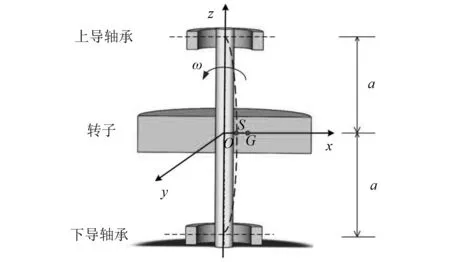
图1 水轮发电机组转子-轴承系统模型图Fig.1 Model diagram of rotor-bearing system for hydro-generator set

为便于分析，对模型作出以下假设：

(1) 将转子简化为一个质量为m1的圆盘，两端采用滑动轴承支撑，且转轴在上、下两端轴承处的集中质量均为m2；

(2) 上、下导轴承对称分布于转子的两侧；

(3) 忽略扭转振动和陀螺力矩，只考虑转子的横向振动。

1.1 不平衡磁拉力

如图2所示，在固定坐标系O-xy内：O′(X,Y)为转子外圆几何中心；δ为任意时刻定转子的气隙长度；δ0为平均气隙长度；α为气隙处与x轴夹角；γ为转子中心旋转角度。

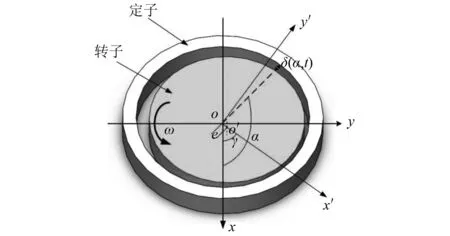
图2 发电机偏心转子气隙示意图Fig.2 Schematic diagram of air gap for generator eccentric rotor

偏心旋转气隙可近似表示为

δ(α，t)≈δ0-ecos(α-γ)

(1)

由文献[29]可知，空载工况下当磁极对数p>3时，根据Maxwell应力积分公式可得到机组不平衡磁拉力(unbalanced magnetic pull,UMP)的解析表达式

(2)

式中：Rr为发电机转子半径；Lr为转子长度；kj为气隙基波磁动势系数；Ij为发电机转子的励磁电流；μ0为空气磁导系数；Λ为气隙磁导Fourier系数。

1.2 非线性油膜力

根据文献[30]，可得非线性油膜力

(3)

(4)

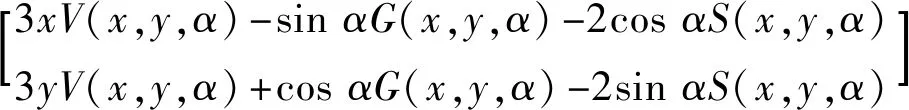
(5)

(6)

(7)

(8)

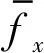
1.3 系统运动微分方程

设轴承轴颈处坐标为(Z,W)，在短轴承支撑假设下导轴承的非线性油膜力为fx及fy，利用Lagrange方程可得系统运动微分方程。为方便计算和讨论，将位移等参量无量纲化

则系统无量纲形式的运动微分方程为

(9)

式中：c1，c2分别为转子及轴承处阻尼；Ke为大轴刚度；e0为转子质量偏心；ω为大轴转速。

2 HB-AFT方法

式(9)为强非线性微分方程，传统的HB方法无法对其进行解析求解。鉴于此，本文通过时域频域转换技术(alternating frequency/time,AFT)对非线性项进行数值形式的Fourier展开，并结合Newton-Raphson迭代方法对方程予以数值求解。

HB-AFT方法在计算时，首先对相关参数进行谐波设解，其次对响应和非线性函数进行谐波平衡化，最后得到其主要使用的方程式。

将X，Y，Z，W和电磁激励及油膜力分别表示为式(10)和式(11)的Fourier级数形式

(10)

式中：ax0，ay0，az0和aw0为常数项；axk，ayk，azk和awk为余弦项系数；bxk，byk，bzk和bwk为正弦项系数；K为所取最大谐波次数。

(11)

式中：cx0，cy0，cz0和cw0为常数项；cxk，cyk，czk和cwk为余弦项系数；dxk，dyk，dzk和dwk为正弦项系数。

将式(10)和式(11)代入式(9)中，经过各阶谐波平衡可得代数关系式g

g(P,Q)=0

(12)

式中：P为由X，Y，Z和W进行Fourier展开后得到的Fourier级数系数所组成的列向量；Q为由非线性力进行Fourier展开后得到的Fourier级数系数所组成的列向量，其表述如式(13)所示

P=[ax0,ay0,az0,aw0,ax1,ay1,az1,aw1,bx1,by1,bz1,bw1,…,axk,ayk,azk,awk,bxk,byk,bzk,bwk]T
Q=[cx0,cy0,cz0,cw0,cx1,cy1,cz1,cw1,

dx1,dy1,dz1,dw1,…,cxk,cyk,czk,cwk,dxk,dyk,dzk,dwk]T

(13)

为获得系统周期解，将Q视为已知，利用不动点迭代方法求解P。本文采用Newton-Raphson方法进行迭代求解

J(i)(P(i+1)-P(i))+g(i)=0

(14)

式中，J为Jacobian矩阵，即J=dg/dP，具体表达为

J=dg(P,Q)/dP=
∂g(P,Q)/∂P+∂g(P,Q)/∂Q·dQ/dP

(15)

由式(13)所得式(15)中的dQ/dP是未知的，需要利用AFT将其变换为已知。

在完成时域信息和频域信息的转换之后，则式(14)中除P以外其余参数均为已知，同时也得到P和Q的关联表达式。在此基础上，可开展相关求解工作。

3 数值模拟及分析

系统主要参数包括：转子质量m1=60 kg，轴颈质量m2=25 kg，转子阻尼c1=4 000 N·s/m，轴承阻尼c2=1 200 N·s/m，转子半径Rr=0.06 m，转子长度Lr=0.15 m，均匀气隙大小δ0=4.5×10-3m，绝对润滑油黏度μ=18×10-3Pa·s，空气磁导系数μ0=4π×10-7H/m，碰摩摩擦因数f=0.01，气隙基波磁动势系数为5.2，励磁电流Ij=4 A，轴承直径Db=50×10-3m；机组转速ω=13 Hz。本文模型主要参数参考文献[31]。

3.1 不考虑UMP时系统周期解

从式(9)可以看出，所研究模型为参数激励系统，T=2π/ω为激励周期。忽略式(9)中电磁激励项Fx_ump和Fy_ump，取谐波次数K=8，时域离散点数N=144，迭代精度设置为10-16。当轴颈间隙cz=1.2×10-3m，长径比Lb/Db=1.0，偏心e0=1.2×10-3m时，利用HB-AFT 方法得到的近似周期解析解为(舍去系数小于10-13的谐波项)

X(t)=0-2.827 999 99×10-2sin(ωt)+
7.345 3×10-13cos(2ωt)+1.926 798×10-11cos(3ωt)-
2.696 9×10-13sin(4ωt)+1.016 16×
10-12cos(5ωt)-1.976 7×10-13sin(6ωt)

(16)

Y(t)=0+2.828 099 99×10-2cos(ωt)+
3.289 1×10-13sin(ωt)-6.719 1×10-13sin(2ωt)-
9.208 6×10-13cos(3ωt)-1.039 88×
10-12sin(4ωt)-3.120 78×10-12sin(5ωt)-
7.096 624×10-13sin(6ωt)

(17)

式中，X(t)，Y(t)为系统受外激励作用得到的周期解。

给定初始迭代值P，通过少量迭代便可得到HB-AFT 的计算结果，如图3所示。从图3中可以看出，其与四阶Runge-Kutta法得到的数值解具有非常高的吻合度，HB-AFT计算准确的特点得以体现。

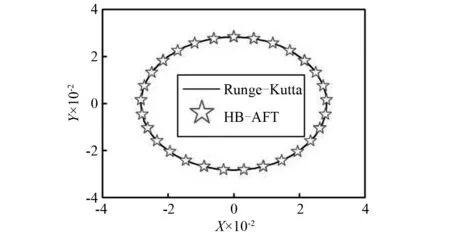
图3 HB-AFT法与Runge-Kutta法计算结果(轴心轨迹)对比Fig.3 The comparison of calculated results (axis trajectory) between HB-AFT method and Runge-Kutta method

当e0=1.2×10-3m，Lb/Db=1.0时以轴颈间隙为控制参数，不考虑UMP作用下转子系统响应分岔图，如图4所示。从图4中可以看出，随着轴颈间隙的增加，系统响应始终保持周期一运动。基于HB-AFT方法，对于系统处于周期一运动的情况，均可以得到类似式(16)、式(17)的周期解，相应其运动轨迹均与Runge-Kutta方法计算结果一致。观察式(16)、式(17)可以看出，系统1倍频值为主要成分，相比之下，其余频谱占比均较为微弱。不过，式中各频谱成分的存在从总体上反映了系统的频域响应特征，故不能对非主导项予以忽略，应从整体层面看待并分析系统的周期解固有属性。而上述结果则证明了HB-AFT在求解水轮发电机组转子-轴承系统周期解的有效性。

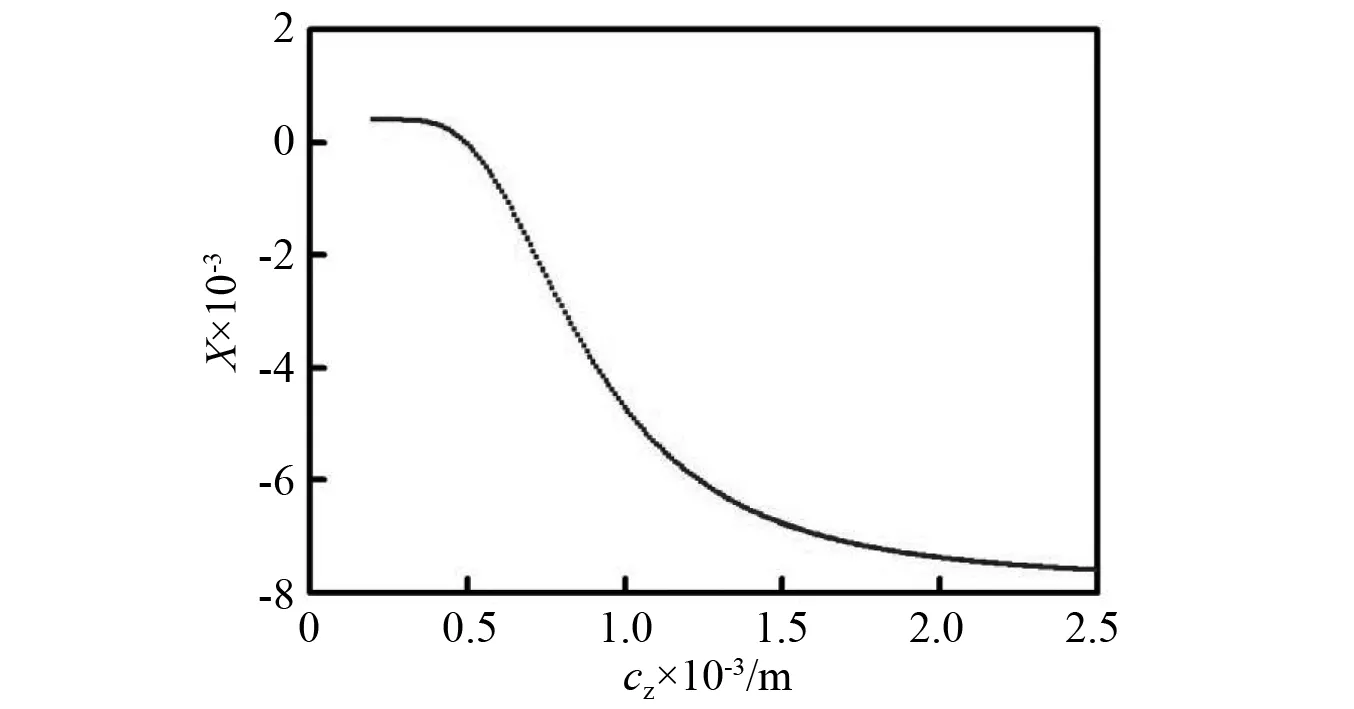
图4 以轴颈间隙为控制参数，不考虑UMP时转子分岔图(e0=1.2×10-3 m，Lb/Db=1.0)Fig.4 The bifurcation diagram of cz on the response of rotor system without UMP (e0=1.2×10-3 m,Lb/Db=1.0)

3.2 考虑UMP时系统周期解

不平衡磁拉力是水轮发电机组的核心外激励之一，在实际运行中会对机组振动产生较大的影响。相同参数设置下考虑UMP后转子随轴径间隙变化分岔图，如图5所示。从图5中可以看出，由于UMP的加入，系统呈现出除周期一外的其他运动形式。当cz=[0.1,0.21]×10-3m时，系统处于周期一运动；随着cz增至0.22×10-3m后，系统变为拟周期运动状态并一直保持，其转子运动轨迹呈现规则形状，映射图吸引子为一封闭圆环，如图6所示。

图5 以cz为控制参数的考虑UMP的系统分岔图(e0=1.2×10-3 m，Lb/Db=1.0)Fig.5 The bifurcation diagrams of cz on the response of rotor system with UMP (e0=1.2×10-3 m,Lb/Db=1.0)

图6 当cz=0.8×10-3 m时考虑UMP后转子轨迹图和庞加莱映射图(e0=1.2×10-3 m，Lb/Db=1.0)Fig.6 Trajectory and Poincaré maps of system with UMP when cz=0.8×10-3 m(e0=1.2×10-3 m,Lb/Db=1.0)

当cz=2.1×10-3时，转子的响应情况如图7所示。

同样取K=8，N=144，迭代精度为10-16，利用HB-AFT 方法得到X与Y方向运动近似解析解为(舍去系数小于10-8的谐波项)

X(t)=2.585 915 47×10-8+2.776 9×
10-8cos(1/5ωt)-4.249 182 94×10-1sin(1/5ωt)-
4.184 94×10-8cos(2/5ωt)-3.489 8×
10-8sin(2/5ωt)-1.517 62×10-8cos(3/5ωt)-
2.476 494 4×10-7sin(3/5ωt)-3.375 225 78×
10-8cos(4/5ωt)-3.513 8×10-8sin(4/5ωt)-
4.258 6×10-7cos(5/5ωt)+3.634 21×
10-8cos(6/5ωt)-2.123 4×10-8sin(6/5ωt)

(18)

Y(t)=1.695 985 15×10-8+4.241 067 045×
10-1cos(1/5ωt)+2.408 747 512×10-7cos(3/5ωt)-
1.667 398 84×10-8cos(4/5ωt)+1.229 599 62×

10-7sin(5/5ωt)+1.065 632 86×10-8sin(6/5ωt)

(19)

从式(18)和式(19)可以看出，与系统处于周期一运动状态时的倍频及多倍频成分叠加(式(16)、式(17))所不同的是，当考虑UMP后，系统呈现以1/5为基础频率及其整数倍成分累加的组合形式。从图7(c)可以看出，频谱图中约0.207 52倍频率占据主导，1.007 08倍频率次之，而0.610 35等频率相比之下由于数值较小未能予以展现，这与式(18)和式(19)在频域方面的表述基本是吻合的。不过，图7(a)的轨迹图不再像周期一运动那般为单一封闭环状，其形状呈相近多圆环缠绕形式，同时观察图7(b)的庞加莱映射图可知，其运动形式为拟周期运动，而利用HB-AFT方法得到的近似解析解(如图7(d)中星型部分所示)虽能在轨迹运行趋势上与图7(a)接近，但该结果仅可近似反映拟周期运动其中一解，对于该解所处具体轨道以及结果的稳定性还需进一步探究。然而，需要指出的是，如仅考虑轨迹的大致变化方向，通过HB-AFT方法获得的结果可为初步预判提供有益借鉴。

图7 当cz=2.1×10-3 m时所得到的响应图Fig.7 The response graphs of rotor system when cz=2.1×10-3 m

4 结 论

本文针对不平衡磁拉力、偏心力和非线性油膜力引起的水轮发电机组转子-轴承系统横向振动问题，通过构建其轴系振动模型，采用半解析半数值谐波平衡-频时转换方法对其周期和拟周期运动进行了分析，并通过数值计算方法对结果的准确性与方法适用性进行了验证。所得结论如下：

(1) 有无UMP作用系统动态特性差异性较为明显。如忽略UMP影响，随轴径间隙变化，转子始终保持周期一运动，利用HB-AFT方法可以从解析层面准确复现系统运动形态。

(2) 当计及UMP后，除周期一运动外拟周期运动得以显现，通过HB-AFT方法虽仅能近似展现非稳态响应其中一解，但可据此判断系统运动大致趋势并基本反映振动响应成分，可为水电机组故障诊断预测提供必要参考。