基于对偶神经网络的动力方程精细积分法

杨 永，李海滨,2

(1.内蒙古工业大学 理学院，呼和浩特 010051；2.内蒙古工业大学 工程训练教学部，呼和浩特 010051)

1994年，钟万勰[1-2]将运动方程转入Hamilton体系，在时域上给出了运动方程以积分形式的解，同时针对该解中的矩阵指数函数提出了精细积分算法，该方法避免了计算机中的截断误差，将矩阵指数的计算精度提高到了计算机的精度。但是由于非齐次项的任意性，如何有效处理精细积分法解中的积分是一个需要解决的问题。Zhong等[3-4]将非齐次项在每个积分区段进行线性化近似，提出了精细时程法，但是精确的递推格式需要对系统矩阵求逆，并且当步长较大时，线性化的假设会导致计算误差增大。为解决这一问题，顾元宪等[5]提出了增维精细积分算法，将非齐次项看做状态变量纳入求解过程中，从而将非齐次项方程转化为齐次方程，保证了计算精度。但是此类算法对非齐次项的形式有一定的要求，只适用于荷载项为几种特殊项的情况。高小科等[6-10]将精细积分与数值积分法相结合，直接对积分解中的积分项进行求解，避免了矩阵的求逆，常用的数值方法有辛普森、科茨、高斯等方法，但由于需要选择积分点，所以需要额外计算积分点的矩阵指数。富明慧等[11-12]利用递推算法和矩形积分公式，提出了广义精细积分算法(generalized precise time step integration method,GPTSIM)，在非齐次项为多项式、指数函数以及三角函数情况下，具有优越的计算性能。但对于其他形式的非齐次项，需要先对非齐次项进行拟合，此时数值解的精度主要取决于非齐次项拟合的精度。王海波等[13]在广义精细积分算法的基础上，结合泰勒级数对其进行了推广，但是实质仍是采用多项式拟合非齐次项。同时，在现有的积分计算方法中，步长对结果的影响较大。选择合适的步长往往较为困难。

本文将精细积分法与神经网络相结合，提出一种基于对偶神经网络的积分算法。不同于其他的数值积分方法，该方法分别利用一组神经网络A和B逼近被积函数和原函数，利用神经网络对任意非线性函数逼近的能力，实现对任意复杂形式函数的积分。本文采用对偶神经网络对精细积分解中的积分项进行计算，在保证高精度的同时，不对非齐次项的形式进行任何假定，同时避免了对矩阵求逆。通过算例，验证了本文方法在任意荷载形式下均有良好的计算精度。

1 精细积分法

在结构动力分析中，一般动力学方程为

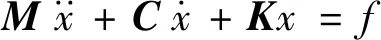
(1)

式(1)的初始条件为

(2)

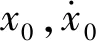
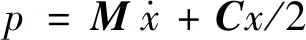
(3)

得

代入式(1)得

(4)

式(4)可以写为

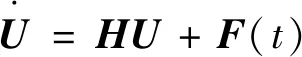
(5)

其中，

此时，式(5)的解可以写为

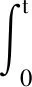
(6)

式(6)为动力方程的解，对其进行离散化处理，记时间步长为Δt，有

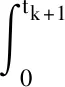
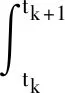
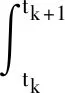
(7)

令T=exp(H·Δt)，得

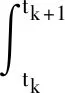
(8)

式中，T为传递矩阵，可利用加法定理精确算得

T=exp(H·Δt)=[exp(H·Δt/m)]m]

(9)

令Δτ=Δt/m，取m=2N,当N取20时，Δτ很小，由泰勒级数可得

exp(H·Δτ)≈I+H·Δτ+(H·Δτ)2/2=I+Ta

(10)

从而

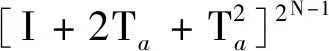
(11)

(12)

由于exp(-x)的存在，上述的积分计算困难。除常用的数值计算方法外，富明慧提出了一种广义积分算法，在式(12)中f(x)为多项式、指数函数和三角函数情况下，广义积分算法可以直接使用。但在实际应用中，荷载项的形式往往很复杂，本文提出一种对偶神经网络积分算法，能够适用于任意形式的荷载项。

2 对偶神经网络积分法的原理

一个对偶神经网络包含A、B两个前向型BP神经网络。其中，神经网络A用来学习积分算式中的被积函数，另一个神经网络B，会通过与神经网络A在权值和激活函数上的特定联系，由神经网络A来确定，用于构建积分被积函数的原函数。神经网络B的结构框图如图1所示。

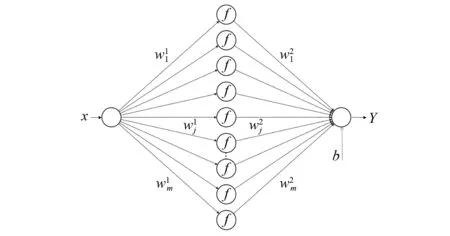
图1 神经网络B原函数示意图Fig.1 Schematic diagram of original function of neural network B

神经网络B中网络输出和输入变量间函数关系如式(13)所示

(13)

对神经网络B确定的函数关系式(13)左右两侧同时对变量x进行求导数，得到式(14)

(14)

令

(15)

则式(14)可以改写为

(16)

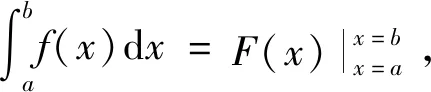
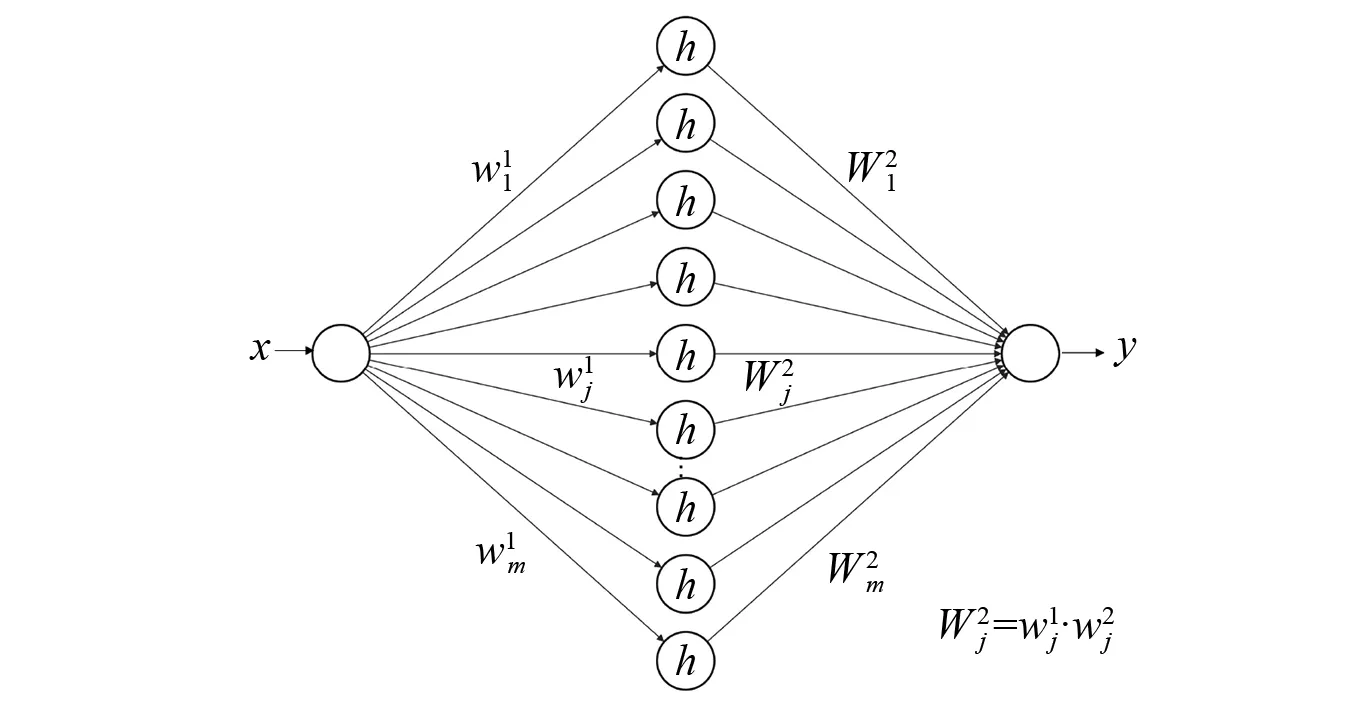
图2 神经网络A被积函数示意图Fig.2 Schematic diagram of integrand function of neural network A

(17)

神经网络A与神经网络B为一对关于变量的积分对偶神经网络，简称对偶神经网络。

式(17)中

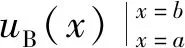
(18)

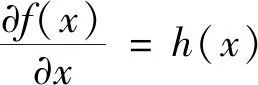
由上述可知，通过训练被积函数样本点集合，则可以通过对偶神经网络方法获得被积函数的原函数，在此基础上，可以根据牛顿莱布尼茨公式得出积分值，至此实现了积分的计算。

3 对偶神经网络求解积分项

对于计算结果中需要进行积分的式(8)

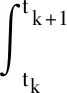
式中，T可由精细算法算得。

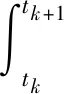
设积分项的被积函数为yk(τ)=exp[H(tk+1-τ)]·F(τ)，其中，H为n×n矩阵，F(τ)为n×1矩阵，输出yk(τ)为n×1矩阵。

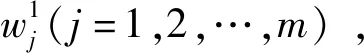
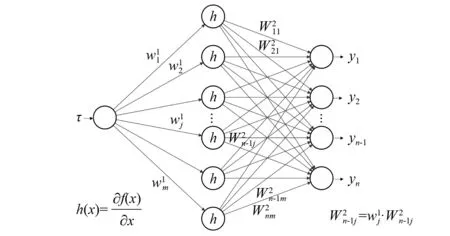
图3 被积函数网络结构示意图Fig.3 Schematic diagram of integrand function network structure

y(τ)=NETAk(τ)

(19)

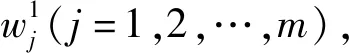
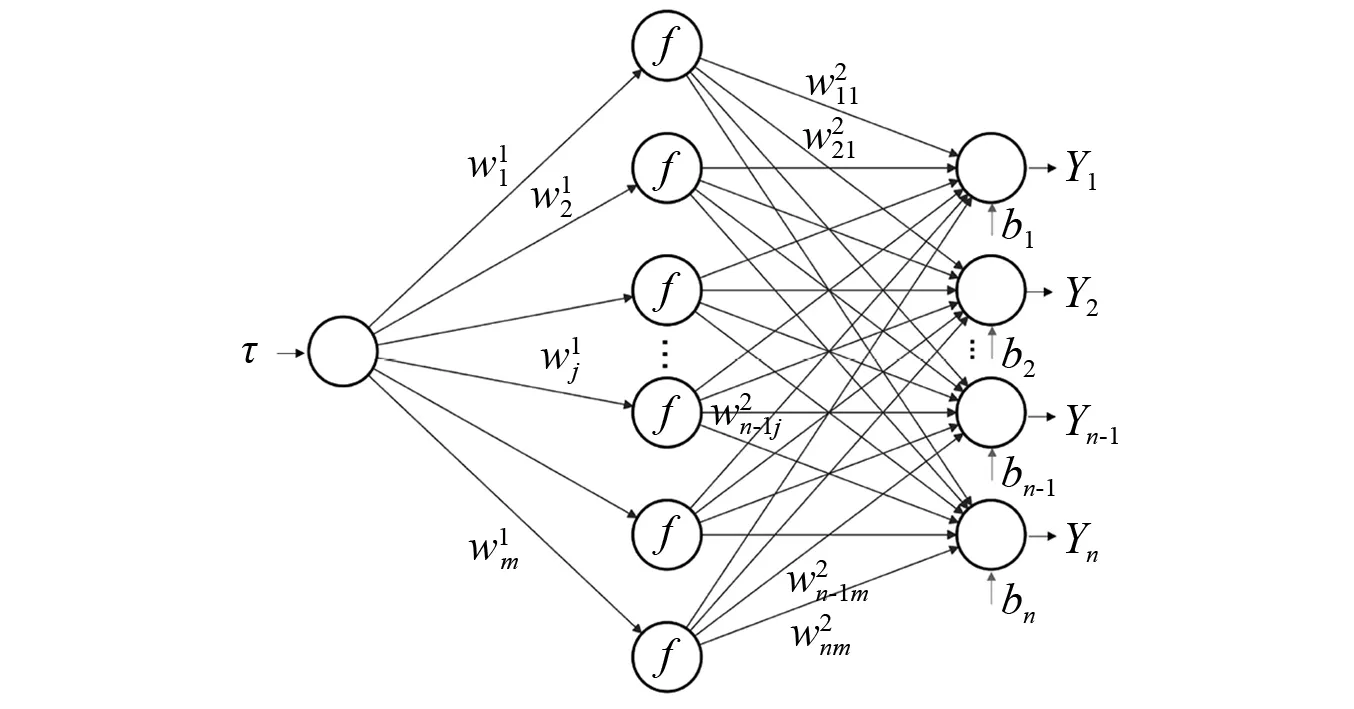
图4 原函数网络结构示意图Fig.4 Schematic diagram of original function network structure

Y(τ)=NETBk(τ)

(20)

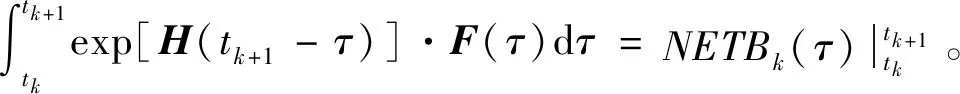
至此，式(8)可以写成

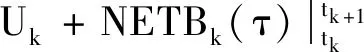
(21)

由上述计算过程可知，对偶神经网络积分法保留了数值积分的特点，在计算过程中只需要各时间点的荷载值，对函数的形式并无任何要求，因此能够适用于任意荷载形式。

4 算 例

算例一

通过上述积分来检验本文算法的精度，同时与富明慧等研究中的广义积分算法进行比较。

广义积分算法选用不同幂级数阶次在t=0处拟合函数ln(1+t)，K为选用幂级数的阶数。

对偶神经网络计算步骤如下：

步骤1构建神经网络A学习被积函数etln(1+t)，隐层和输出层的激活函数分别为sigmoid、purelin，神经网络层数为3层，隐层单元个数为30，输入层单元个数为1，输出层单元个数为1。

步骤2将t的取值范围[0,0.1]进行50等分取值构成网络A输入样本，计算函数etln(1+t)的值做为网络A的输出样本。

步骤3训练神经网络A，训练误差设置为1×10-6，最大训练步数2 000。训练完成后，由式(15)即可得到原函数网络B，神经网络B的隐层和输出层激活函数分别为softplus、purelin。

计算结果如表1所示(表中结果加粗字体部分为与精确解不同部分)。

表1 神经网络积分法和广义积分法结果与精确解比较Tab.1 Comparison of the results of neural network integration method and GPTSIM with the exact solution

由表1中数据可以看出，广义积分法在幂级数阶数较低的时候精度较差，随着幂级数拟合阶数的提高，精度逐步提高。这是因为广义积分法中需要先采用幂级数对积分项进行拟合，然后利用递推格式得到积分结果。而一些复杂函数在幂级数拟合过程会产生较大的误差，所以广义积分法的精度取决于拟合精度。而对偶神经网络积分法采用一个神经网络A拟合积分项，根据万能逼近原理，一个三层神经网络能够逼近任意函数，在神经网络A无限逼近被积函数的同时，神经网络B无限逼近原函数。通过调整隐层单元的个数，对偶神经网络积分法能够达到高精度。通过对比，神经网络在拟合样本容量为50的情况下就已经达到与五阶广义积分法解的同等精度，表明了本文对偶神经网络积分具有较高精度。同时，通过提高样本容量，也能进一步提高对偶神经网络的积分精度。

算例二

运动方程

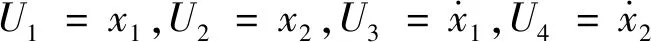
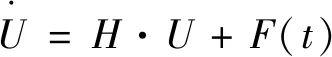
其中，

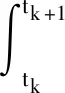
步骤1构建神经网络A学习被积函数exp[H(tk+1-τ)]·F(τ)，由于H为4×4矩阵，F(τ)为4×1矩阵，因此设置神经网络A的输出层单元个数为4，其输入层单元个数为1，隐藏层单元个数为30，隐层和输出层激活函数分别为sigmoid、purelin。

步骤2将τ在区间[tk,tk+1]范围内100等分取值构成神经网络A输入样本，计算函数exp[H(tk+1-τ)]·F(τ)的值做为神经网络A的输出样本。

步骤3训练神经网络A，训练误差设置为1×10-6，最大训练步数2 000。训练完成后，由式(15)即可得到原函数网络B，神经网络B的隐层和输出层激活函数分别为softplus、purelin，神经网络B的网络权值由神经网络A确定。

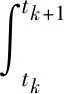
为便于比较，取与解析精细积分法相同步长0.28。计算结果如表2所示(表中结果加粗字体部分为与精确解不同部分)。

表2 x1,x2位移Tab.2 Displacement of x1,x2

从表2中数据可以看出，在荷载为常数荷载时，精细时程积分的计算结果与精确解在有效位数内完全一致，具有足够的计算精度。这是因为精细时程积分法假设非齐次项在步长[tk,tk+1]范围内是线性的，当荷载项为常数时，由于步长时间较小，精细时程积分的线性化假设对计算结果影响较小。但是精细时程积分法在计算中需要对矩阵H求逆，限制了精细时程积分法的应用范围。而对偶神经网络积分法对积分项进行直接积分，使用神经网络对积分函数进行逼近，因此不涉及矩阵求逆，同时可以看出，神经网络积分法的计算结果在有效位数内与精细时程积分完全一致，说明了对偶神经网络积分在避免矩阵求逆的同时也保证了精度。而威尔逊-θ法随着时间的增长，误差不断增大。

算例三

运动方程

本算例的荷载为非线性正弦荷载，其解析解为

分别采用精细时程积分以及直接积分法中的科茨公式、高斯公式和GPTSIM与本文对偶神经网络积分法进行对比。GPTSIM采用泰勒级数展开形式下的广义精细积分法，并经过精度修正。

由于对偶神经网络计算积分对函数形式没有要求，因此算例三对偶神经网络积分法的网络结构参数与算例二相同，神经网络A的输出层单元个数为4，输入层单元个数为1，隐藏层单元个数为30，训练误差设置为1×10-9，最大训练步数5 000。计算步骤也与算例二相同。

计算结果如表3所示(为方便比较，列出x1的值，表中结果加粗字体部分为与精确解不同部分)。

表3 x1位移Tab.3 Displacement of x1

算例3的激励为正弦荷载，具有振荡性。由表3数据可以看出，不同于常数荷载，在非线性荷载情况下，精细时程积分法的计算结果随着时间的增加，精度明显降低，这是因为时程积分在对时间域内的荷载进行了线性化假设，而非线性荷载线性化产生的误差会随着时间增长不断累积，导致计算结果误差也不断增大。科茨公式、高斯公式在正弦荷载情况下给出了较高精度的解，说明了传统的数值积分方法仍是保证动力方程精细积分高精度的有效积分算法。GPTSIM和对偶神经网络算法在6位有效数字内都与精确解一致，GPTSIM是在荷载为多项式、三角函数、指数函数情况下归纳出的一种递推算法，因此本算例中GPTSIM精度较高，对于其他形式的荷载，需要先拟合成三次样条函数、傅里叶级数、泰勒级数等形式。因此与精细时程积分法类似，GPTSIM的误差除了计算误差外，还来源于拟合误差。而对偶神经网络对荷载形式没有任何要求，同时还保证了计算的高精度。

5 结 论

(1)本文基于精细积分法和神经网络，提出了一种用于求解动力方程的计算方法。该方法针对动力方程在哈密顿体系下得到的积分形式的解，利用一组神经网络同时逼近被积函数和原函数，从而实现解中积分项的求解。计算过程中避免了矩阵求逆，具有对步长不敏感、不用对非齐次项进行假设等优点。最后通过算例表明，本方法是神经网络与精细积分的有效结合，是一个精准有效的算法。

(2)本文方法是对精细积分法的一种拓展，利用对偶神经网络方法对动力方程哈密顿体系下积分解中的涉及到的积分进行求解，将精细积分法的应用范围拓展到线性荷载、简谐荷载以外的任意非齐次项形式。同时，对偶神经网络积分法本质是一种数值积分计算方法，能够适用于大部分积分问题，具有广阔的应用前景。