基于声学虹吸效应的水下低频大宽带吸声机理研究

马承志，王立博，吴 晓，吴九汇

(1.西安交通大学 机械工程学院，西安 710049；2.西安交通大学 机械结构强度与振动国家重点实验室，西安 710049)

近年来，声学超材料因其对低频声的良好吸声性能而得到迅速发展。与传统材料相比[1-5]，如多孔材料、穿孔或微穿孔板，超材料能够实现以更小的结构尺寸达到更高的能量耗散效率。到目前为止，已经获得了一系列新的超材料，其中大部分能够以亚波长厚度实现声音近乎100%的吸声，包括膜型超材料[6-11]，声学超材料[12-18]，缠绕空间超材料[19-22]，慢波超材料[23-26]，亥姆霍兹谐振器[27-28]。目前，空气声吸声材料已经逐步趋于成熟，水下吸声材料也有不错的研究进展[29-40]，但水下全频段的吸声尤其是低频段仍需进一步研究突破。因此，实现水下低频高效吸声成为当前的研究热点和科学挑战之一。

在前人工作和研究的基础上，我们提出了一种水下薄板型超材料，该超材料具有多个元胞可以具有多个低频吸声峰。在该多元胞结构作用下其同一位置处共振峰值频率较单个元胞结构略微变化，但吸声性能仍能保持较高的水平。更具体地说，在压差声汇机理作用下，整个入射声能被迫从周围元胞流向某一元胞，从而提高了元胞的振动强度，振动幅值大大提高，进而将声能转化为弹性应变能在结构阻尼的作用下实现了能量的耗散，表现出良好的吸声效果。在声学虹吸效应作用下单个元胞的自振特性基本没有改变，因此峰值频率大体上保持不变或略微变化。此外，通过深入研究该效应作用下的吸声机理及其对吸声性能的影响，本文正式提出基于声学虹吸效应的低频大宽带吸声机理，为超材料设计提供更好的物理解释。

论文结构如下:第一部分，介绍了基于声学虹吸效应的低频大宽带吸声机理的薄板型超材料；第二部分，通过压差声汇机理、声阻抗匹配机理及等效负动态质量密度机理验证了该薄板型超材料的低频大宽带吸声性能；第三部分，详细研究了面积比及主要参数对薄板型超材料吸声性能的影响；第四部分，对薄板型超材料的各项参数进行合理设计优化，实现了水下100～500 Hz的低频大宽带吸声效果；第五部分，进行了总结。

1 薄板型超材料有限元模型

1.1 模型建立情况

为了说明低频大宽带吸声机理，给出了两种模型，单元胞结构(元胞一)如图1(a)所示和元胞一元胞二组合的双元胞结构如图1(b)所示，元胞二是通过改变元胞一的参数而得到的新元胞。该单元胞结构由三部分组成:一块矩形的薄板，薄板由复合钢板[41-46]构成，两个相同的半圆形铅块和一个声学刚性框架。计算中使用的材料参数如表1所示。元胞一是将两个直径d1=104 mm、高度均为h1=37.5 mm、间距D1=104 mm的半圆块分别对称固定在薄板上，薄板的宽度W=150 mm、长度L=300 mm、厚度S=1.2 mm。薄板的边界固定在声学刚性框架上，该框架为上下贯通的通腔，壁厚t=3 mm。元胞二是在元胞一的基础上对部分参数进行了调整，半圆块直径d2=110 mm、高度h2=105 mm、间距D2=110 mm，其他参数均与元胞一相同。

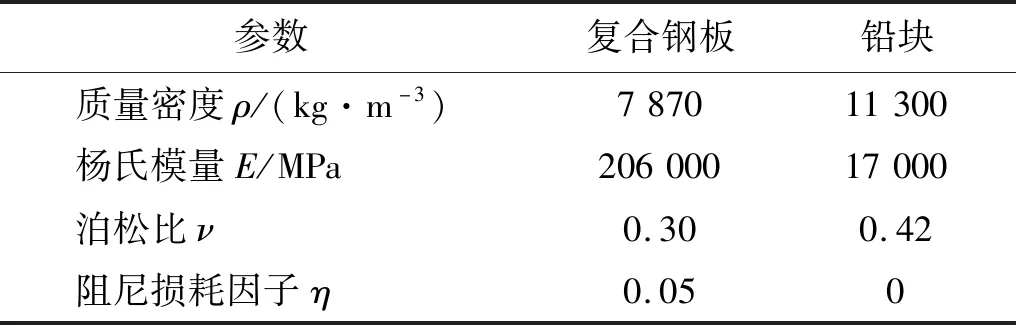
表1 计算所用到的材料参数Tab.1 Calculate the material parameters used

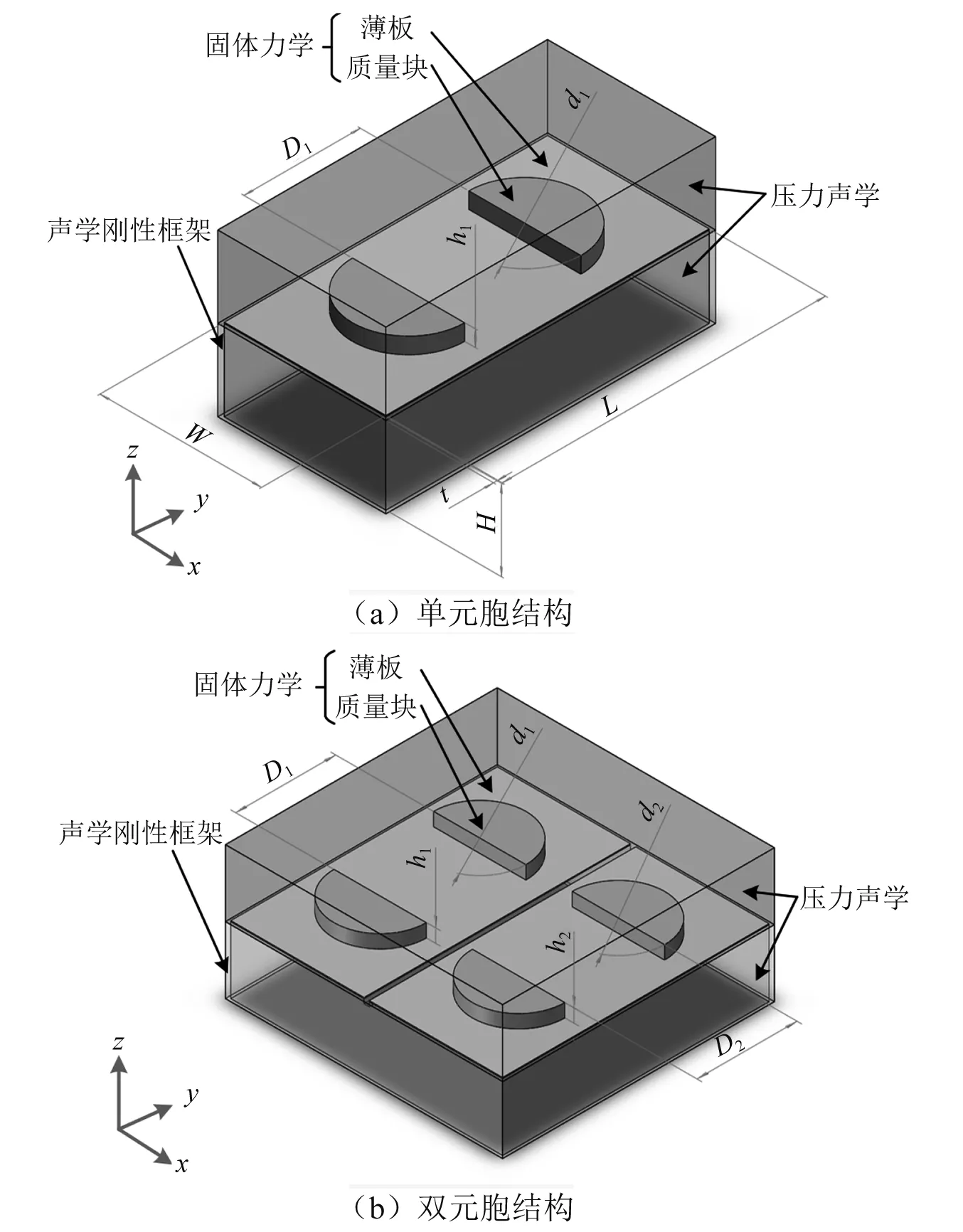
图1 仿真模型Fig.1 Simulation structure

为了获得该超材料的吸声性能，利用商用有限元软件COMSOL MultiphysicsTM 5.6建立了声-固耦合的有限元仿真模型。薄板、质量块被定义为固体域，其余部分被定义为声学域；沿z轴负方向，将平面入射波P=10 Pa垂直地施加于该超材料表面；边界条件设置为固定约束，该约束施加在每个元胞薄板的外边缘；材料参数和几何尺寸与上述参数保持一致。此外，水的密度和水中的声速分别为ρ0=1 000 kg/m3和c0=1 500 m/s。

根据能量守恒定理，入射声波Ii的能量转化为以下三部分组成：反射声波Ir的能量、透射声波It的能量以及声能转化为结构共振后所耗散的能量Iα。因此，该超材料所耗散的能量Iα可以表示为

Iα=Ii-Ir-It

(1)

声强吸声系数α定义为Iα和Ii的比值

(2)

式中：RI为声强反射系数；TI为声强透射系数[47]。

在不考虑声波传播过程中媒质损耗问题情况下，薄板质量块吸声结构其吸声系数α≤50%[48]

(3)

式中，pia和pta分别为入射声波和透射声波的声压幅值。

1.2 共振模态分析

薄板型超材料的吸声是声能转化为弹性应变能在结构阻尼作用下来实现能量耗散的结果，共振时，可以实现最大的能量耗散。图2给出了单元胞结构(元胞一、元胞二)及双元胞结构的吸声系数及共振模态。通过对比可以看出，在双元胞结构下元胞一具有一个吸声峰，对应451 Hz处的共振模态:半圆质量块直边的平移、扭转运动加上薄板中心的剧烈振动；元胞二具有两个吸声峰，分别对应143 Hz和312 Hz处共振模态，从而使得双元胞结构获得了三个吸声峰。值得注意的是，与单元胞结构的吸声峰相比较，双元胞结构在对应频率处的振动模态基本上不发生改变，质量块的主要振型不会发生大的改变，但振动幅值增加，吸声峰值频率略微改变，仍然具有很好的吸声效果。在第一个吸声峰和第二个吸声峰之间有一个比较小的峰值，主要是因为当该频率的声波入射到双元胞结构表面时，该双元胞结构在此频率处产生了一个新的微小的共振，该共振与其他频率处的强烈共振相比较较为微弱，该结构主要是通过结构共振在结构阻尼的作用下耗散能量进行吸声，所以达不到很好的吸声效果，出现了一个比较小的峰值。

图3(a)和图3(b)显示了声能量流在吸声频率为451 Hz时双元胞结构中的分布，从图中可以看出，在元胞一和元胞二之间的表面压差作用下，使得大部分入射能量从周围区域流向元胞一。如图2(b)和图2(g)所示，元胞一的振动幅值从47×10-6mm 提高到8×10-5mm，与单元胞结构(元胞一)相比，双元胞结构的声学虹吸效应增强了单元胞结构(元胞一)质量块的振动。特别是图2(h)所示的总弹性应变能，在共振频率处，双元胞结构的总弹性应变能约为单元胞结构的两倍多。所以当吸声面积是入射面积的一半时，双元胞结构仍然具有有较高的吸声系数。总而言之，声学虹吸效应虽然增强了振动，但主要共振元胞的固有振动特性基本保持不变，并且其他元胞相较于共振元胞来说，振动振幅很小或基本保持不动，使得整体结构对应的峰值频率变化不大只是略微进行了移动，具有很好的吸声效果。该研究表明在多元胞情况下，入射能量增大，在某一元胞的作用下将周围的声能量抽吸过来，使得该元胞处的能量增强，进而振动的能量增强，质量块振动的幅值增大，元胞结构的弹性应变能增大，从而将声能转化为弹性应变能在结构阻尼作用下进行耗散，在面积变大的多元胞结构中仍然具有很好的吸声效果。在后面的章节中，将具体讨论该超材料吸声的物理机理，同时为了排除其他因素的干扰，更好地体现面积比对该薄板型超材料吸声的影响，我们对不同面积比情况下单元胞的吸声性能也进行了相应的研究。

图2 结构的吸声及振动情况Fig.2 Sound absorption and vibration of the structure

2 薄板型超材料吸声的多重物理机理分析

2.1 压差声汇机理

本节以薄板型超材料的双元胞结构为例，通过理论分析来解释压差声汇机理。

双元胞结构如图1(b)所示，假设吸声结构由两个元胞组成:元胞一和元胞二，其中两元胞表面声阻抗率分别为Zs1，Zs2。

(4)

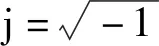
当平面波从z<0区域垂直作用于元胞表面时，入射声压场Pi和反射声压场Pr可表示为

(5)

式中：pia为入射声压振幅；ω为角频率；k为波数；γ为反射声压幅值的放大系数；σπ为入射波和反射波之间的相位差。

因此，总声压场P为

P=piaexp(jωt)[exp(-jkz)+γexp(jkz+σπ)]

(6)

水中粒子速度为

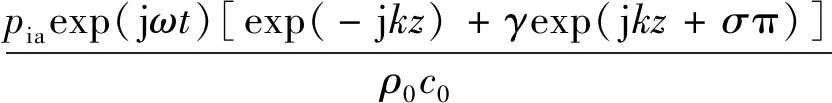
(7)

式中，ρ0c0为水的特征阻抗。

由式(6)和式(7)可得结构表面声阻抗率，并由此获得在z=0处的声阻抗率

(8)

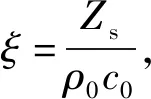
(9)

因为Zs=Rs+jXs,Rs和Xs分别为声阻率、声抗率，所以声阻抗率比还可表示成

ξ=xs+jys

(10)

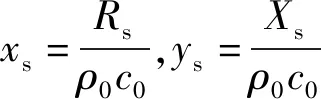
(11)

元胞一和元胞二的表面压力表示为

(12)

最后，给出两元胞之间的表面声压差Δp

Δp=piaexp(jωt)[γ2exp((σπ)2)-
γ1exp((σπ)1)]

(13)

正是阻抗不匹配引起的表面压差导致了声能量在水中运动，产生了声学虹吸效应，如图3(a)和图3(b)所示。

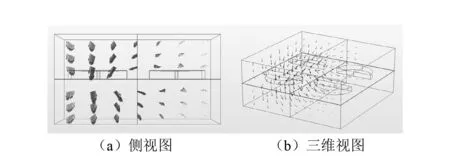
图3 声能量情况Fig.3 The case of sound energy

以双元胞结构为例，我们可以看出当312 Hz的声波入射时，此时的吸声效果及阻抗匹配情况是最为理想，元胞二几乎满足阻抗匹配条件xs2≈1和ys2≈0；元胞一则可以看作是xs1≈∞ 和ys1≈1，入射波几乎完全反射。据此得到元胞一与元胞二之间的表面压差方程式为

Δp=-piaexp(jωt)

(14)

在这种压差作用下，入射能量被迫从周围区域流到双元胞的元胞二，更多的能量被增强的振动吸收。

2.2 声阻抗匹配机理及等效负动态质量密度机理

声阻抗匹配机理是指多元胞情况下整体声阻抗Z0对吸声面积比η的变化不敏感，当吸声面积比降低时，整体结构的声阻抗没有成比例增强。具体分析如下:

对单个元胞阻抗的理论模型进行了分析，简化的原理图如图4(a)所示。单个元胞的声阻抗是ZM，这里的薄板-质量块系统可以等效于质量-弹簧系统[50]，其声阻抗为

(15)

式中：R为由振动强度决定的薄板的等效阻尼；M1取决于质量块的质量；K1取决于薄板的刚度。

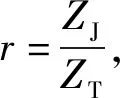
(16)

可见随着面积比的减小，多元胞中的声阻抗并没有成比例变大。根据声阻抗匹配机理，100%的吸声只能通过Zrc=ρ0c0，Zim=0。其中Zre和Zim分别是Z0的实部和虚部。即在共振频率处，具有较好的吸声效果。

声学虹吸效应可以使得多元胞结构具有较为匹配的声阻抗，因而具有较好的吸声效果，这对设计具有宽带吸声效果的紧凑结构具有重要的研究价值。

等效负动态质量密度机理指的是该结构的等效质量密度在吸声系数峰值所对应的频率处为零，如图4(c)所示，由牛顿第二定律，可以看出当系统处于零等效质量状态时，结构受力时自身会产生一个很大的加速度，系统会产生很大的响应，形成共振。在该结构中我们可以把该薄板-质量块系统等效于三组元振子模型[51]如图4(b)所示，其等效质量密度为

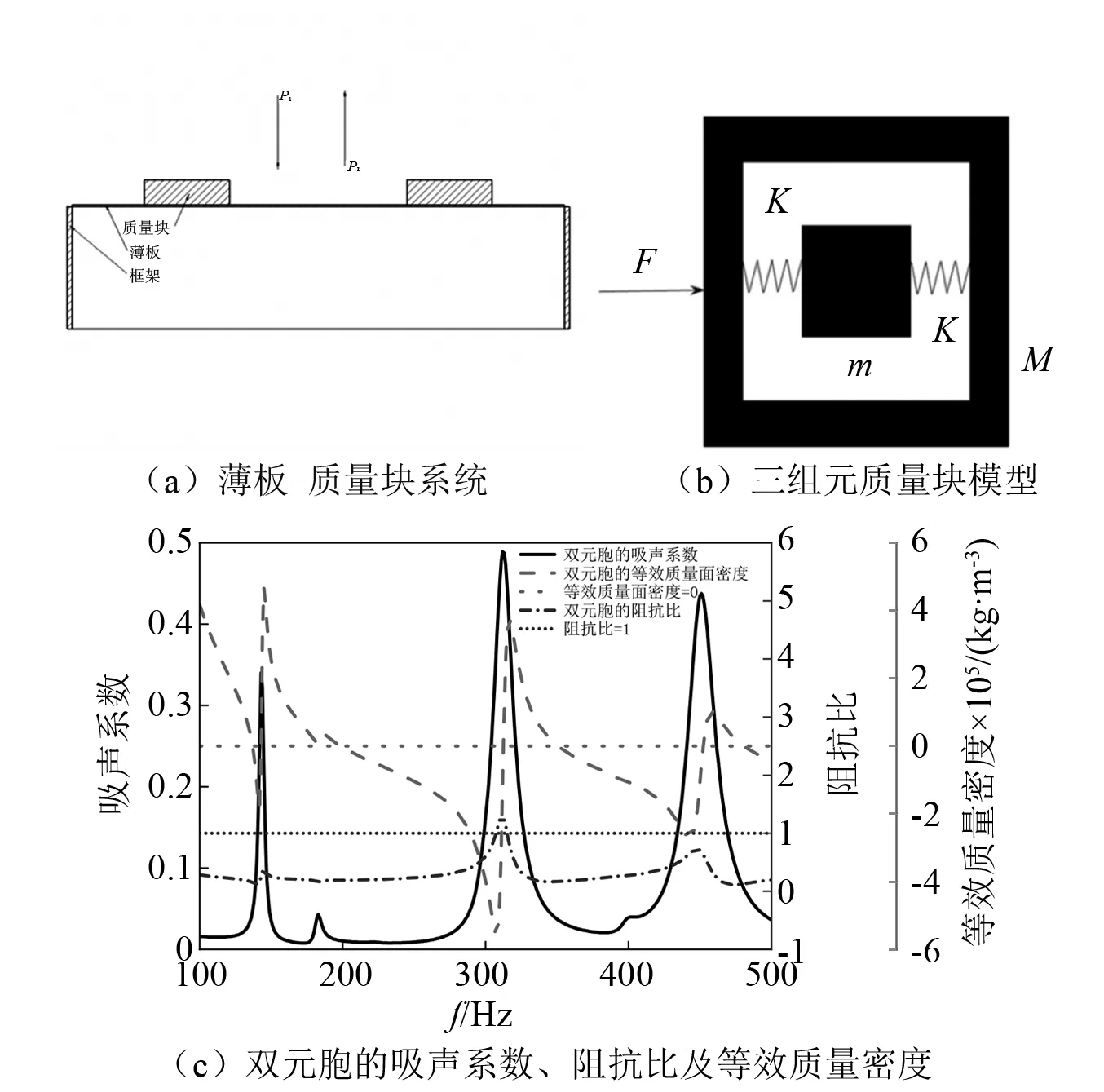
图4 系统模型情况Fig.4 The case of the system model

(17)

式中：M2由复合钢板的质量决定；m由振子的质量决定；K2取决于薄板的刚度。

薄板类声学超材料的吸声特性也是基于零等效质量效应，通过系统的共振模式产生大量的能量耗散从而增强结构的吸声性能。

3 面积比及主要参数对吸声性能的影响

本节详细研究了该薄板型超材料在不同面积比下的吸声性能，为后续的宽带吸声结构设计提供指导；同时对该结构的主要影响参数进行了研究。

3.1 不同吸声面积比的吸声性能

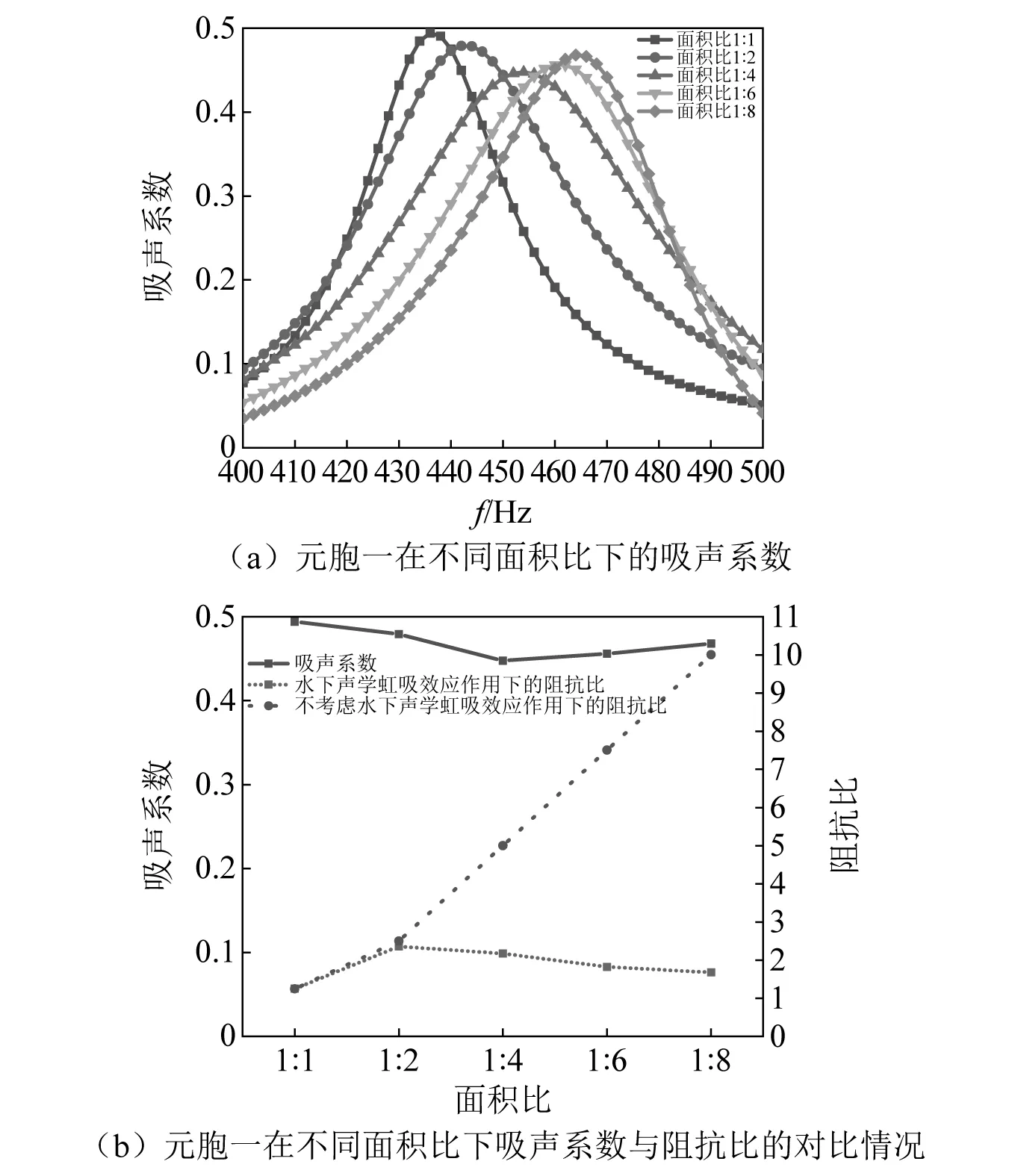
图5 面积比对吸声情况的影响Fig.5 The effect of area ratio on sound absorption

3.2 主要参数对吸声性能的影响

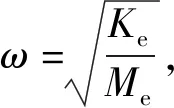
下面我们分别研究了在吸声面积比为η=1情况下单元胞结构(元胞一)的薄板厚度S和质量块高度h1对吸声性能的影响。

图6(a)为不同薄板厚度S对元胞一结构吸声性能的影响，S依次为1.0 mm，1.1 mm，1.2 mm，1.3 mm，1.4 mm。可以发现，随着S从1.0 mm增大到1.4 mm，吸声峰值频率逐渐向高频移动，仍然具有很好的吸声效果。

图6(b)为不同质量块高度h1对元胞一结构吸声性能的影响，在这里h1分别取元胞一原质量块高度的0.8倍、1.0倍、1.2倍、1.4倍和1.6倍。可见质量块的高度对峰值频率有较大的影响。随着质量块高度的增加，吸声峰值频率逐渐向低频移动，同样具有很好的吸声效果，这为我们向低频吸声的调节打下了良好的基础。

图6 主要参数对吸声性能的影响Fig.6 Influence of main parameters on sound absorption performance

4 基于声学虹吸效应的水下低频大宽带超材料

基于上述分析，图7(a)给出了一种由单元胞结构平行排列组成的薄板型超材料，具体来说，薄板型超材料的整体尺寸分别为W=150 mm，L=200 mm，H=49 mm。

通过对每个元胞结构的大小进行合理设计，使得每个元胞结构尽可能利用声学虹吸效应，同时通过对每个元胞结构的薄板厚度以及质量块的大小、位置、高度的调节，使得每个质量块在共振频率处对应一个吸声峰值，最终实现了100～500 Hz的低频大宽带吸声效果如图7(b)所示。

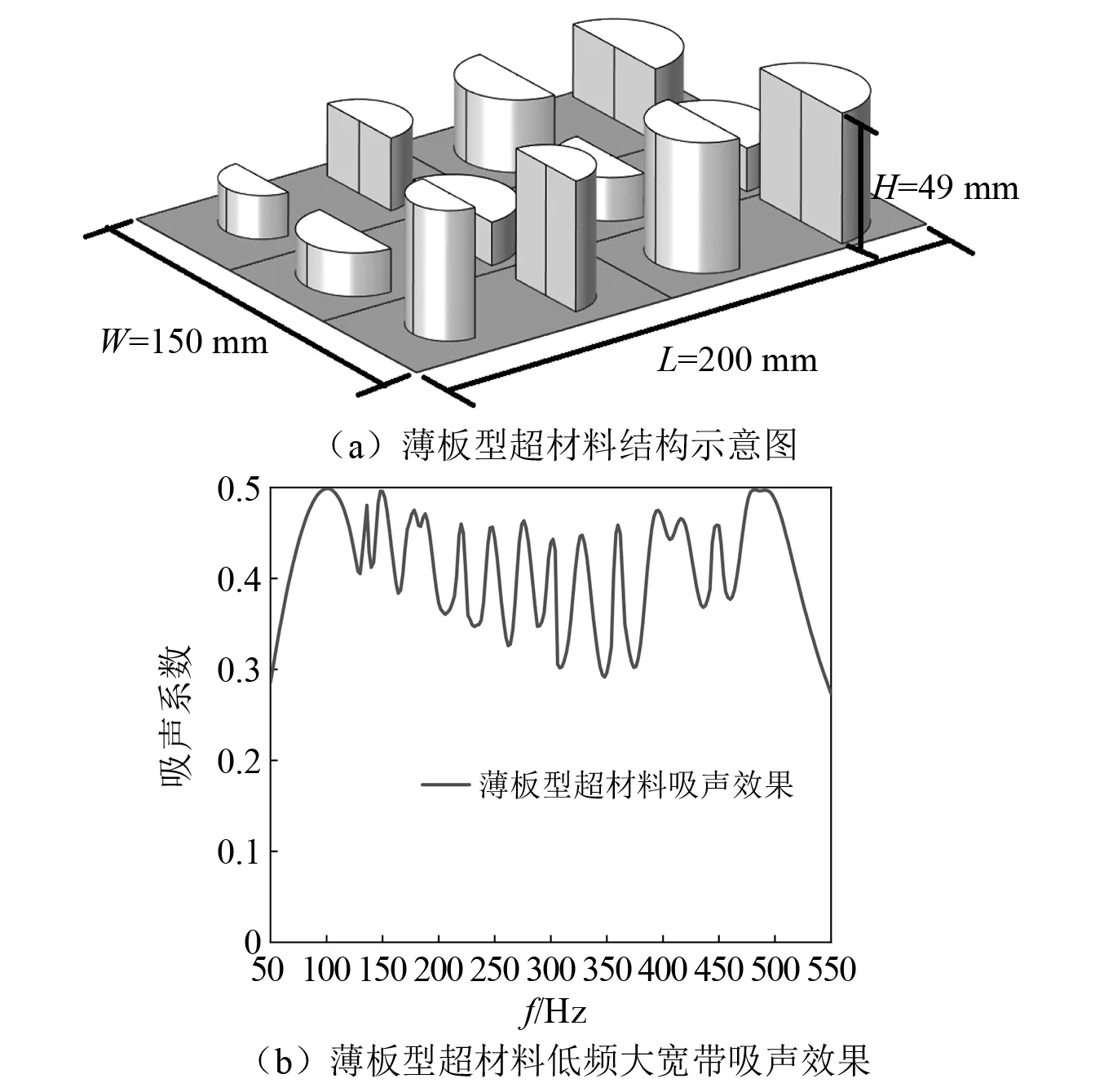
图7 低频大宽带吸声Fig.7 Low-frequency and wide-band sound absorption

5 结 论

在本研究中，我们提出并详细研究了基于声学虹吸效应的水下低频大宽带吸声机理，在声学虹吸效应的作用下，不同面积比下的吸声元胞可以使几乎所有的入射声能量通过元胞的振动被耗散掉，使得整体仍然保持着较好的吸声性能。我们详细分析了该超材料的压差声汇机理、声阻抗匹配机理、等效负动态质量密度机理，验证了该超材料的低频大宽带吸声性能。同时研究了主要参数对吸声元胞性能的影响，得出了非常重要的规律。因此，在不受试验条件限制的情况下，采用一定多的元胞可以进一步提高吸声性能，实现大宽带吸声。总之，本研究将为水下低频大宽带吸声的设计提供有效的指导，并显示出巨大的水下声波控制潜力。