基于隐式Adams方法的螺旋曲面铣削系统稳定性预测研究

杨赫然，耿超绪，孙兴伟，董祉序

(沈阳工业大学 机械工程学院，沈阳 110870)

加工过程的振动及抑制策略直接影响螺杆转子铣削加工质量和加工精度，并可对机床及刀具产生严重损害[1]。加工过程中的振动形式主要有再生颤振和强迫振动两种[2]。再生颤振是一种强烈的自激振动，亦是高性能机床在加工过程中必须控制的主要振动形式[3]。按照产生机理[4]，颤振可以分为再生型颤振、振型耦合型颤振、摩擦型颤振、力-热耦合型颤振等。

其中，再生型颤振往往先于其他形式发生，也是金属切削过程中主要的颤振形式[5]。

为了防止螺旋曲面铣削加工过程中再生颤振对加工的影响，加工前有必要对螺旋曲面铣削稳定性进行预测，以保证加工时能够延长刀具的使用寿命并且获得较高的表面质量[6-7]。

针对再生型颤振对精工的影响，通常用线性时滞微分方程来表示再生型颤振影响的铣削加工动力学模型[8]。所以如何能够获取时滞微分方程精确的解，且获得稳定性叶瓣图，是预测螺旋曲面铣削系统稳定性的关键。

到目前为止，预测铣削稳定性的方法有很多种，主要分为时域法、频域法和试验方法。

时域法包括半离散法、全离散法和时间有限元方法等。Insperger等[9-11]提出半离散法，该方法对时滞微分方程中的时滞项进行离散，其算法的精度与离散步长呈正相关，基于半离散法，又提出改进半离散法以及高阶半离散法。Niu等[12]提出基于Runge-Kutta的分析方法。Li等[13]提出了另一类全离散法，该方法离散了所有时间相关项，利用数值迭代方法得到迭代公式，从而得到Floquet转移矩阵。Ding等[14]基于时间有限元法，以积分方程技术求解铣削动态系统响应，提出数值积分法，并将其发展为具有指数收敛阶的谱方法和针对多时滞工况的变步长法[15]。Ding等[16-17]提出全离散方法，包括一阶全离散法和二阶全离散法，一阶全离散是通过线性插值对状态项和时滞项进行离散，二阶全离散法是通过Lagrange插值对状态项进行离散，通过线性插值对时滞项进行离散。Guo等[18]通过牛顿插值提出了三阶全离散法，能够得到更高的计算精度和更快的计算效率。Zhang等[19]基于Simpson公式提出了一种全新的方法预测铣削稳定性。

频域法一般为将颤振模型的时滞微分方程组利用傅里叶变换转到频域表示，基于控制理论，解析计算铣削稳定边界。Budak等[20-21]提出了频域法求解铣削动力学方程，但这种方法的计算精度无法满足小径向切深。Merdol等[22]提出了多频率法，该方法考虑了定向因子的高次谐波，然而在计算过程中需要迭代搜索颤振频率，需求解多个特征值。Bachrathy等[23]将多频率法扩展到适用于所有刀具结构的稳定性预测，包括可引入分布时滞的复杂刀具结构，将扩展多频率法和多维二分法结合以提高计算效率，并证明了在所测频响函数质量较差的情况下，扩展多频率法依然可以得到可靠的稳定预测结果。

综上所述，众多学者针对铣削加工过程的稳定性预测进行了较深入的研究，然而随着新算法的涌现，在预测精度及速度上仍有较大的提升空间，且针对不同动力学系统的适应性有进一步探究的必要。

Adams作为典型的线性多步法代表，当插值区间较大，计算步数较多时，由于其参与运算的函数个数较其他算法少，因此在计算效率方面具有明显优势。智红英等[24]针对单自由度及双自由度高速铣削系统进行预测研究，也表明该方法在效率及精度方面优势明显。螺杆转子铣削动力学模型为三自由度动力学模型，需要在保证预测精度的同时提高预测速度，因此，本文基于隐式Adams方法对螺旋曲面铣削系统的稳定性进行预测，探究隐式Adams方法对螺杆转子铣削动力学模型的适用性，为螺旋曲面铣削加工稳定性预测提供理论依据。

1 动力学模型建立

对于多自由度系统，预测铣削稳定性的再生颤振动力学模型，可以用时滞微分方程进行表示，如式(1)所示

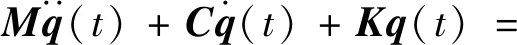
(1)

式中：M为模态质量矩阵；C为模态阻尼矩阵；K为模态质刚度矩阵；q(t)为模态坐标矩阵；H(t)为周期系数矩阵；Tc为刀齿周期(时滞量)，Tc=60/(Nn)；N为刀具齿数；n为主轴转速；ap为切削深度。

1.1 三维铣削力模型

在铣削螺杆转子曲面时，由于数控系统中给出的进给量沿着工件Zw轴方向，而刀具沿着Xc轴上下移动，且刀具存在摆角，所以总的进给量由Zw向及Xc轴复合而成。因此，首先要建立铣削力模型，如图1所示[25]。

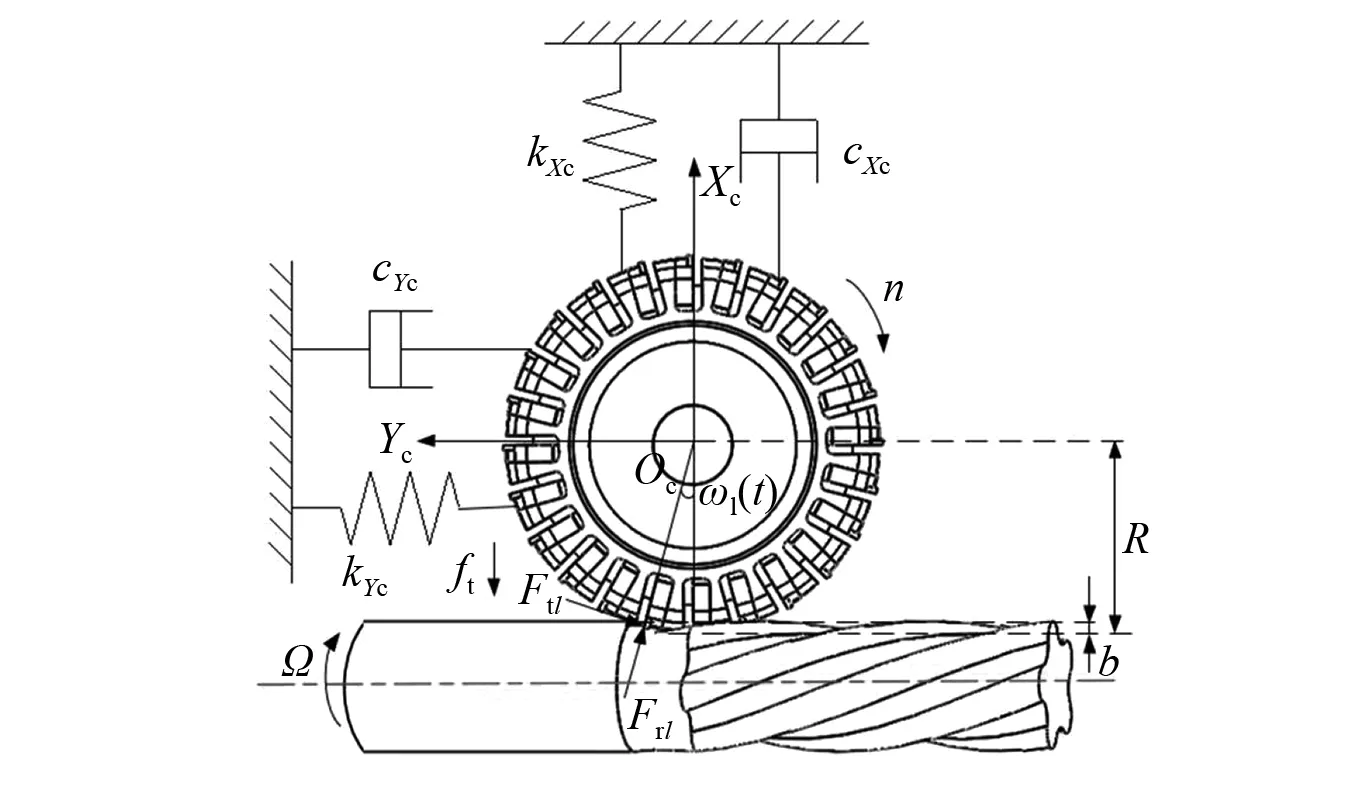
图1 铣削力模型Fig.1 Milling force model

以瞬时刚性切削理论为依据，铣削过程中的瞬时切削厚度、切向铣削力，径向铣削力、轴向铣削力的表达式如式(2)和式(3)所示

(2)

(3)

式中：ΔXc，ΔYc和ΔZc分别为Xc，Yc和Zc方向上盘铣刀铣削螺杆转子曲面时产生的动态位移；ft为横向进给率；fT为轴向进给率。由于决定铣削稳定性的是动态铣削力，所以忽略静态铣削力，将切向铣削力Ftl、径向铣削力Frl和轴向铣削力Fal分别映射到刀具坐标的Xc，Yc，Zc，可以得到三个方向的力如式(4)所示

(4)

1.2 三自由度动力学模型

随后在建立三自由度力学模型的-基础上建立动力学模型，如图2所示。

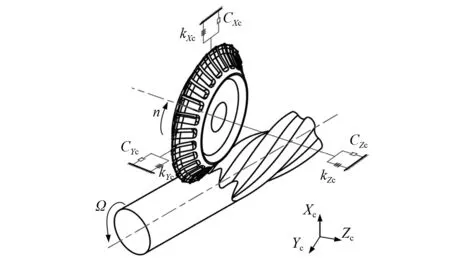
图2 三自由度动态铣削动力学模型Fig.2 Three-degree-of-freedom dynamic milling dynamic model

则铣削动力学模型可以由下列方程进行表示

(5)

式中：mtx，mty和mtz为刀具Xc，Yc和Zc方向的模态质量；ξx，ξy和ξz为Xc，Yc和Zc方向的阻尼比；ωnx，ωny和ωnz为Xc，Yc和Zc方向的固有圆频率。

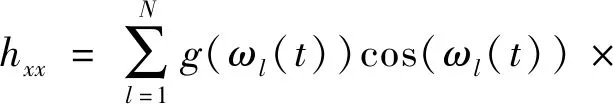
(6)

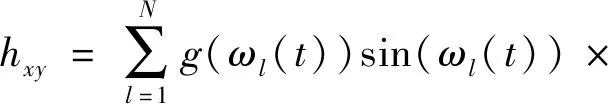
(7)

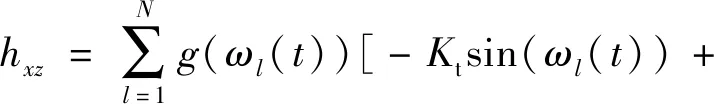
(8)

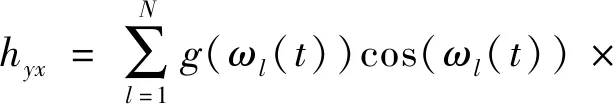
(9)

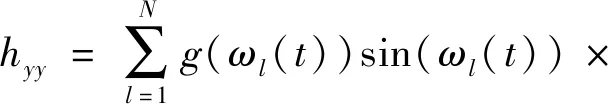
(10)

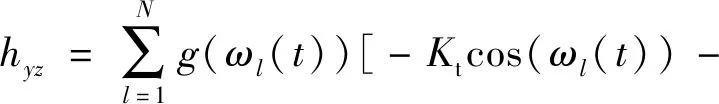
(11)

(12)

(13)

(14)

式中：Kt为切向切削力系数；Kr为径向切削力系数；Ka为轴向切削力系数；ωl(t)为第l个刀齿的位置角。

(15)

式中：ωst为刀具的切入角；ωex为刀具的切出角。对于顺铣ωst=arccos(2b/D-1)，ωex=π；对于逆铣，ωst=0，ωex=arccos(1-2b/D)，其中b/D为径向切深和直径的比值。

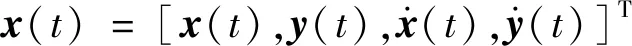
(16)

其中，

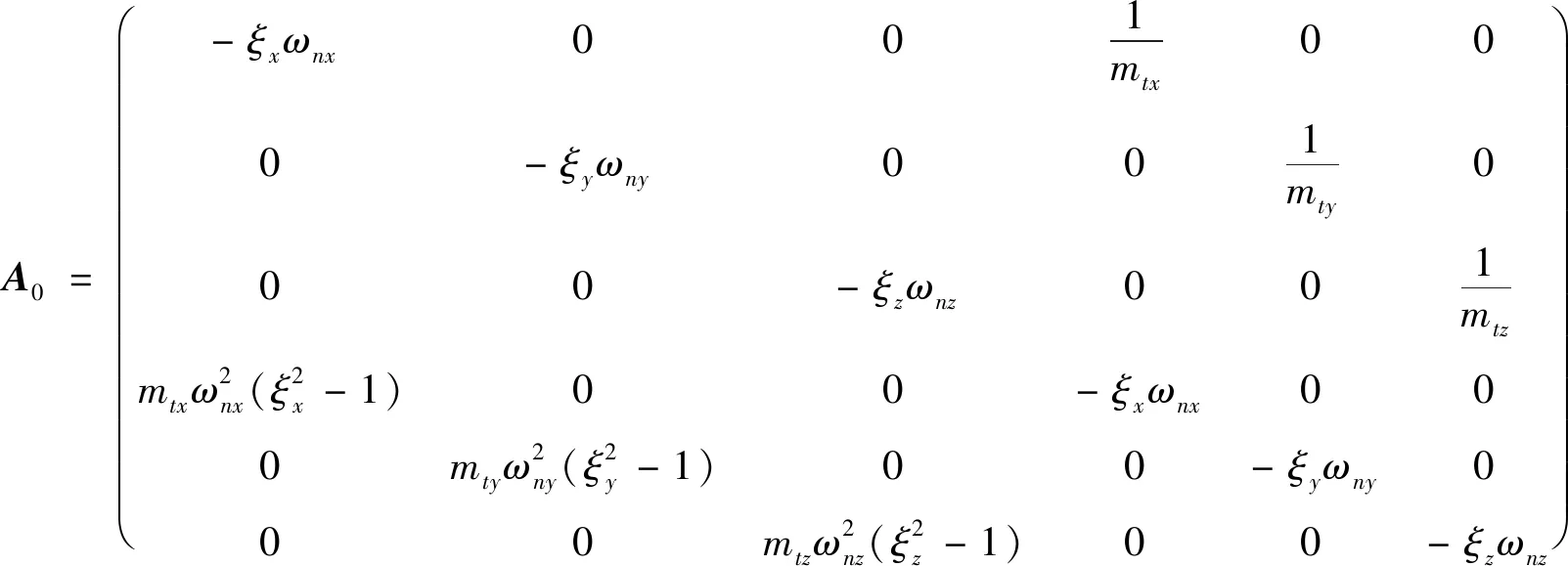
(17)

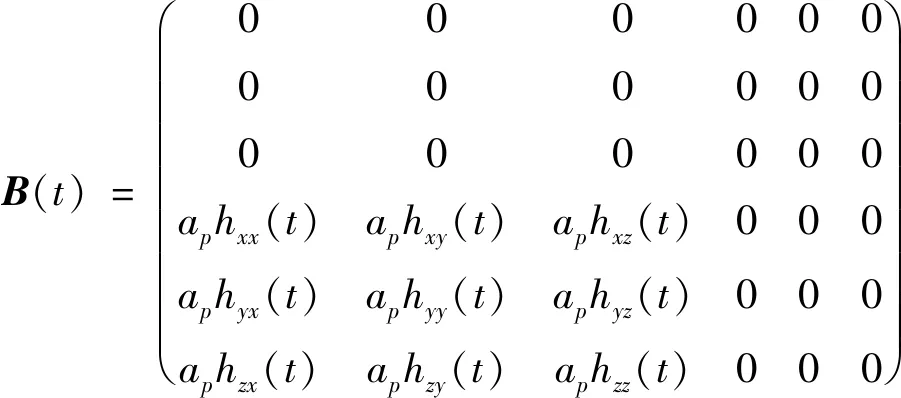
(18)

2 参数识别

若要精确的求解动力学模型，需要获取盘铣刀的模态参数，介于盘铣刀结构特点，仅通过试验不易获得三个方向的模态参数，因此本章采用模态试验与仿真结合的方法，获取盘铣刀的模态参数。对装配状态下的盘铣刀进行模态分析，获得各阶振型。

2.1 盘铣刀装配状态下的模态仿真分析

为精确分析盘铣刀动态特性，采用有限元分析软件对装配状态下的盘铣刀部件进行模态分析，得到其前六阶振型，其中前两阶如图3所示。前六阶振型的变形方向均围绕Z轴，且X、Y、Z向模态参数相同。

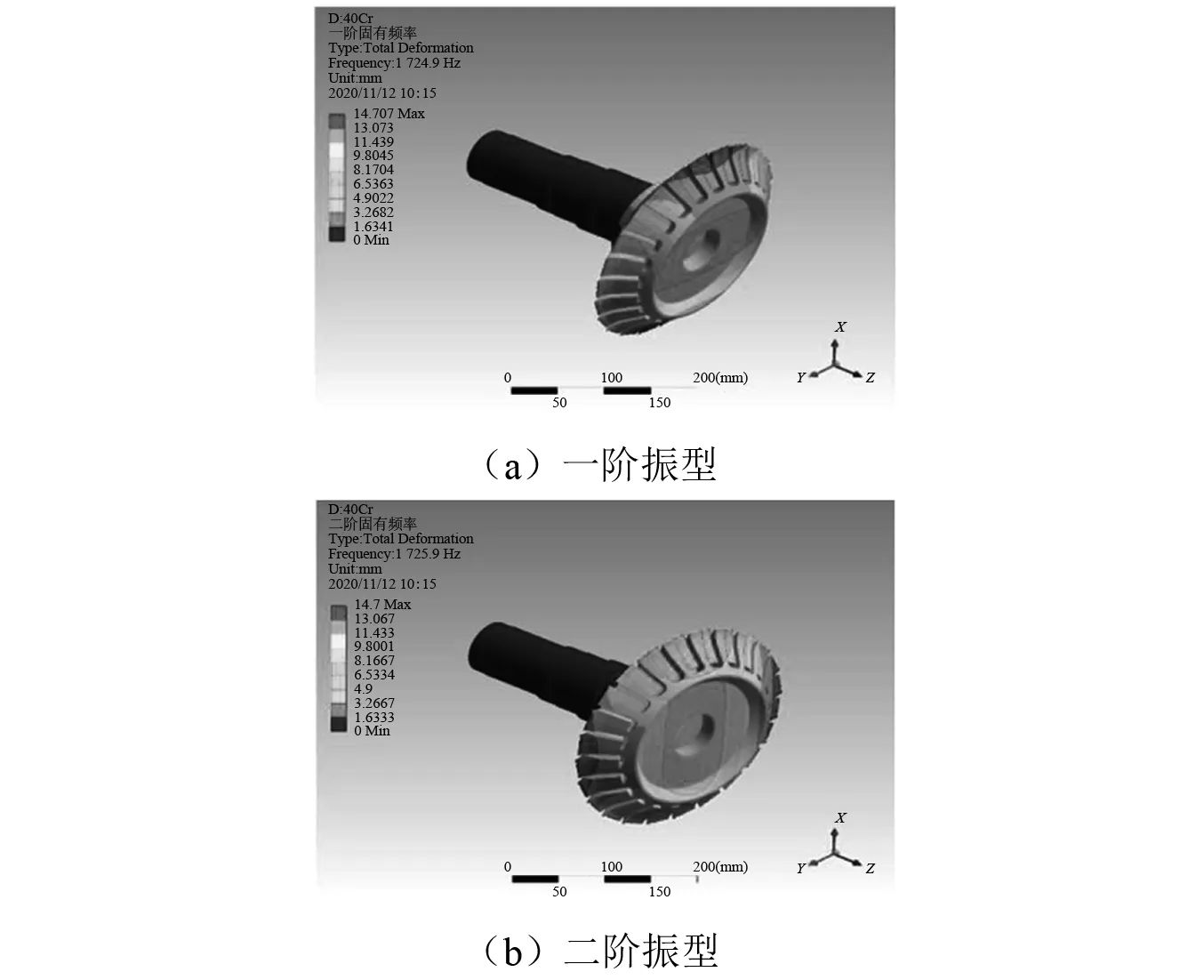
图3 装配状态下的盘铣刀前两阶模态振型Fig.3 Mode shape of disc milling cutter in assembly state

2.2 盘铣刀装配状态的谐响应分析

在模态仿真分析的基础上进行谐响应分析可获取其位移响应所集中的位置，同时为模态试验提供支撑依据。根据振型图，在盘铣刀形变位移最大的位置，选取三个位置分别施加300 N的简谐作用力，方向沿着刀具Z轴负方向。将谐响应分析求解的最大频率范围设置为10 000 Hz，求解间隔设置为400，基于2.1节模态分析进行求解，得到盘铣刀的时间位移响应，如图4所示。

通过图4可知，Xc方向的响应频率峰值出现在1 725 Hz，3 925 Hz和4 400 Hz附近，Yc方向的响应频率峰值出现在1 725 Hz，1 800 Hz，3 925 Hz和4 400 Hz附近，Zc方向的响应频率峰值出现在1 725 Hz，3 925 Hz和4 400 Hz附近。由模态分析得到的盘铣刀装配状态下1阶～6阶的固有频率分别为：1 724.9 Hz，1 725.9 Hz，1 788.7 Hz，3 919.6 Hz，4 430.5 Hz和4 432.2 Hz，由于盘铣刀存在重根模态的影响，故会出现重复频率。因此在盘铣刀装配状态下谐响应分析0～10 000 Hz频率范围内，盘铣刀装配状态下1阶～6阶固有频率容易激发。

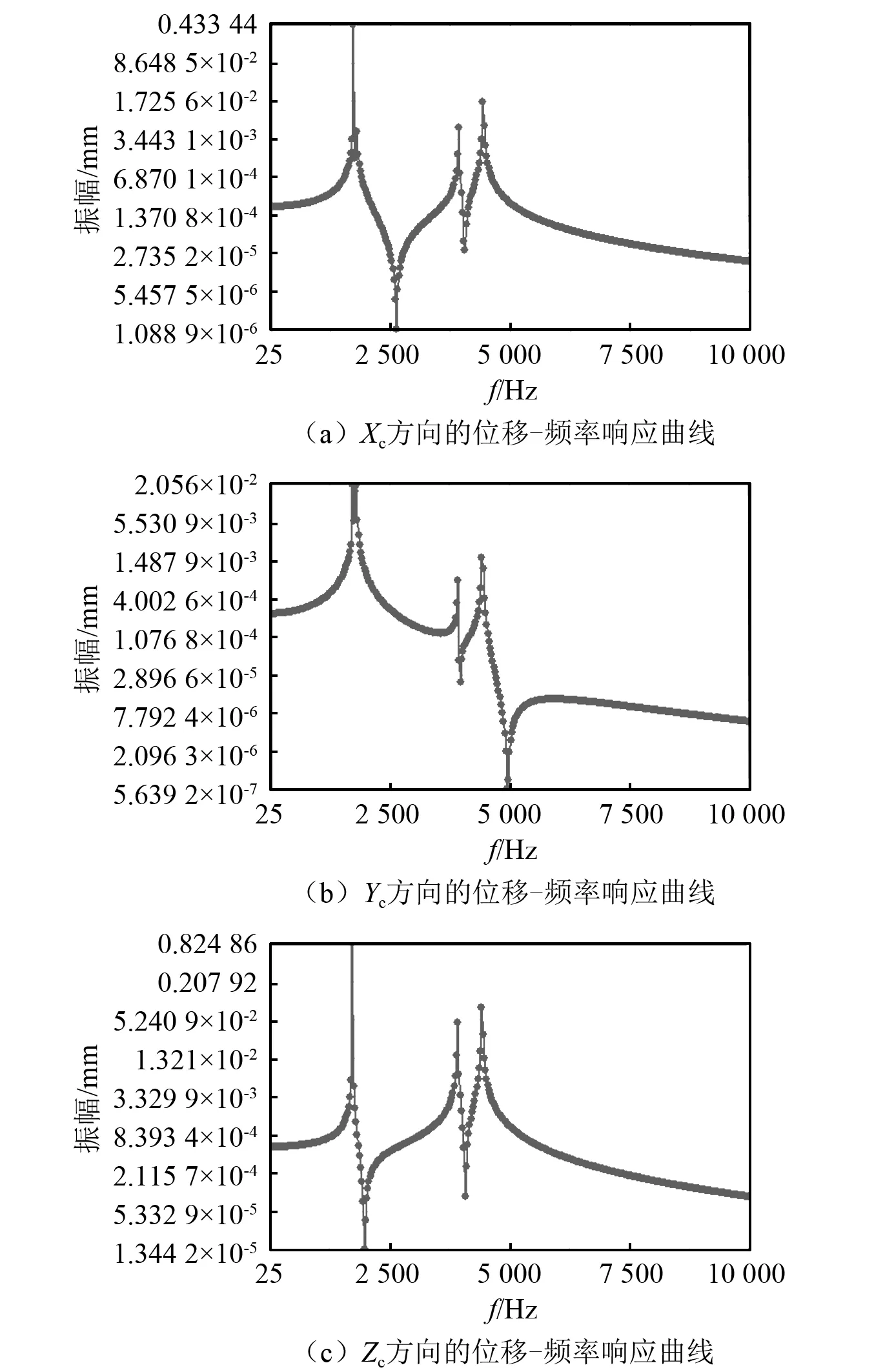
图4 Xc，Yc，Zc位移-频率响应曲线Fig.4 Frequency response curve in Xc,Yc and Zc directions of the assembled state of disc milling cutter

2.3 模态参数获取试验

本次试验采用锤击法获取盘铣刀的刀尖频响函数曲线，试验采用DEWEsoft公司的SIRIUS-ACC数据采集器，力锤和加速度传感器采用IEPE型，试验过程采用移动力锤法。根据模态仿真分析可知，盘铣刀在装配状态下前6阶的模态振型不同且出现重根模态，根据模态振型位移最大位置布置传感器。传感器在盘铣刀的布置点以及试验台布局分别如图5和图6所示。图5中，按顺时针方向对传感器进行编号分别为1号、2号、3号和4号传感器，根据传感器布点位置，力锤敲击产生振动后即可获得所关心频率范围内的传递函数。

图5 传感器布置示意图Fig.5 Schematic diagram of sensor arrangement

图6 试验装置示意图Fig.6 Schematic diagram of experimental device

由频响函数参数估计的基本方程中留数和模态振型之间的关系和模态振型矩阵的互易性可知，矩阵的每一列元素，都包含模态振型的信息，因此只要模态振型在Xc，Yc和Zc方向存在与参考自由度相关的振型，则测量数据就能观察到模态信息。

每隔一个刀齿选取一个锤击点，尽可能多的选取锤击点数，试验采样频率设置为10 000 Hz，谱线数设置为8 192条，根据Nyquist理论，所能获取的频率窗口长度为采样频率的一半，经计算得采样频率的分辨率为0.61 Hz。根据传感器布点，试验获取的传递函数曲线及相干性曲线如图7和图8所示。通过图7的幅频特性曲线可以获取模态的固有频率以及阻尼比等模态参数信息。模态试验获取的相干性曲线，反应了响应是否和激励相关，当响应是由激励引起时，相干性曲线的值接近1，则说明两者相关。反之，则不相关。

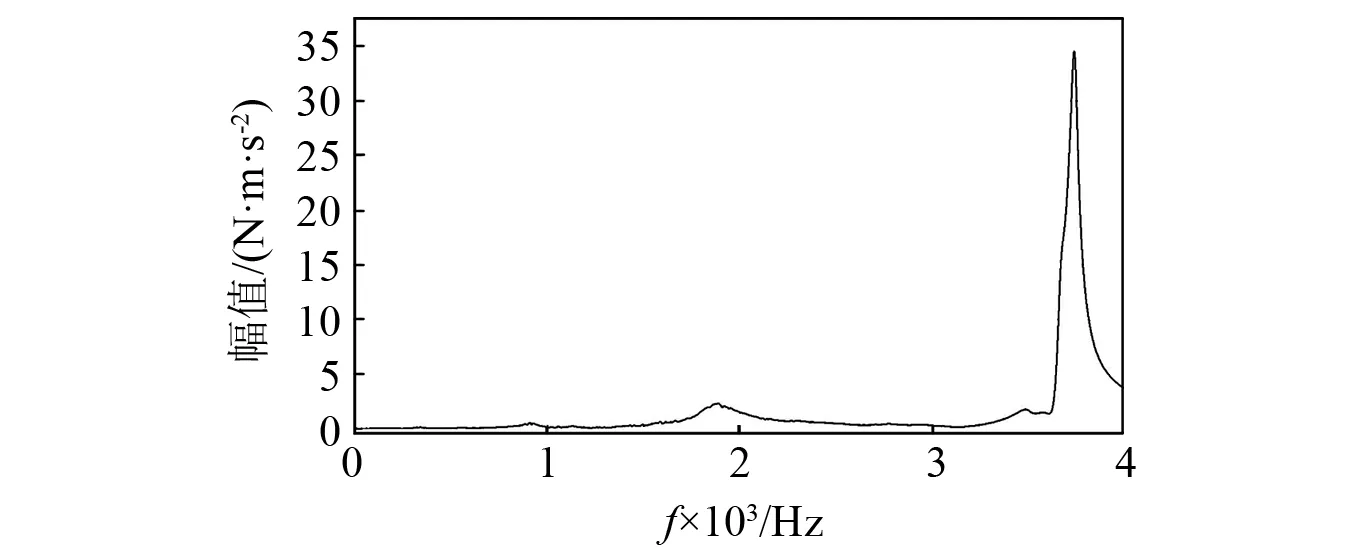
图7 传递函数幅频特性曲线Fig.7 Amplitude-frequency characteristic curve of transfer function

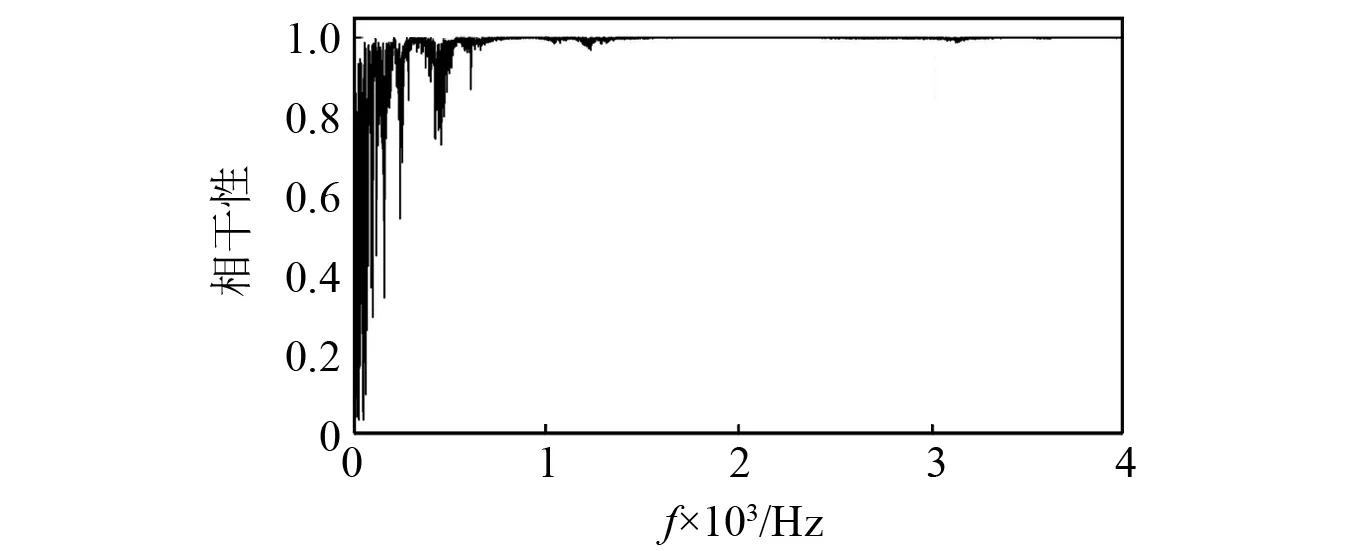
图8 相干性曲线Fig.8 Coherence curve

根据模态仿真分析结果、模态试验数据以及传感器布点位置综合分析可知，试验数据中的一阶频率对应模态仿真中的第三阶固有频率，其中的二阶频率对应模态仿真分析中的第四阶固有频率。

除1号和2号传感器测量的数据外，3号和4号传感器的数据分别与1号和2号的数据非常接近，说明盘铣刀具有良好的对称性，但动态特性又稍有区别，并非完全对称。将试验数据与模态仿真数据进行对比分析可知，两者的误差均在10%以内，如表1所示。由此可知仿真结果具有较高可信度。

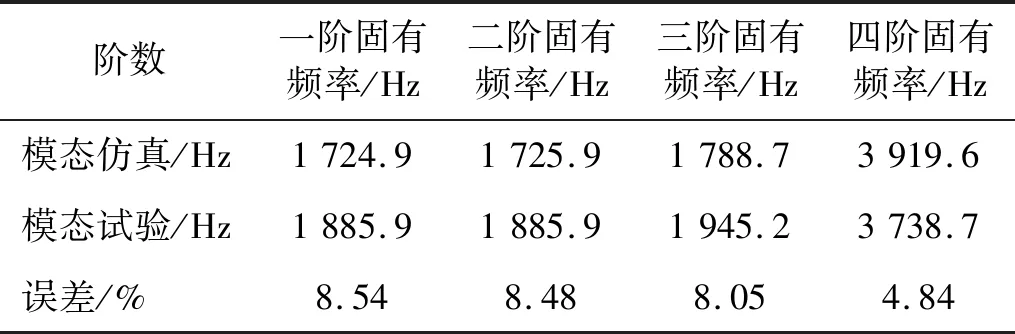
表1 盘铣刀装配状态模态试验与模态仿真结果对比Tab.1 Comparison of assembly state modal experiment and simulation results of disc milling cutter

2.4 基于导纳圆拟合法的模态参数识别

导纳圆拟合法是一种比较直观的方法，可以在数据质量稍低时，在一定数据范围内搜索出峰值，拟合出峰值频率。

根据传递函数幅频特性曲线以及相干性曲线，可以判断出本次试验数据良好。根据模态试验数据以及导纳圆拟合方法分析得到的数据如表2所示，表2中固有频率、阻尼比、模态质量和模态刚度对应仿真数据中的第一、第二和第四阶模态信息。由模态仿真分析可知，盘铣刀X、Y、Z三向的模态质量、模态阻尼及模态刚度分别对应相等，因此以表2中的一阶模态参数作为后续稳定性预测的计算数据。

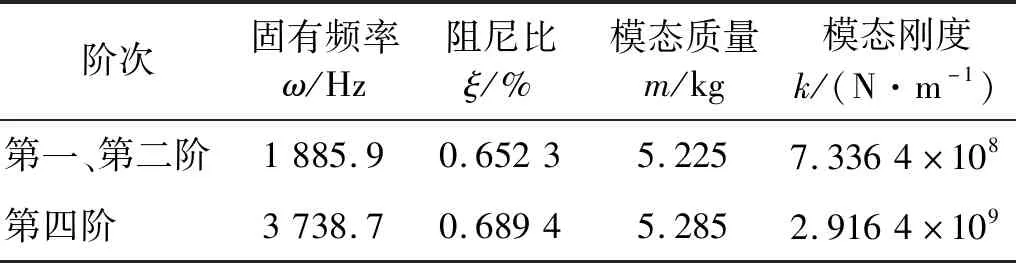
表2 盘铣刀试验模态参数Tab.2 Test modal parameters of disk milling cutter

2.5 平均切削力系数识别

刀齿在一个铣削周期的平均铣削力可以表示为

(19)

由于颤振和表面粗糙度等因素的影响，使刀具的每个旋转周期测得的力都存在一定差值，因此选取刀具切削螺杆转子1/5的切削力，即5头螺杆切削过程的1/5部分所测得的瞬时铣削力数据的平均值作为平均铣削力，使用定积分计算不同的铣削加工参数下的平均铣削力数据，50 mm棒料作为试验材料，试验加工参数由正交试验法获得，如表3所示。

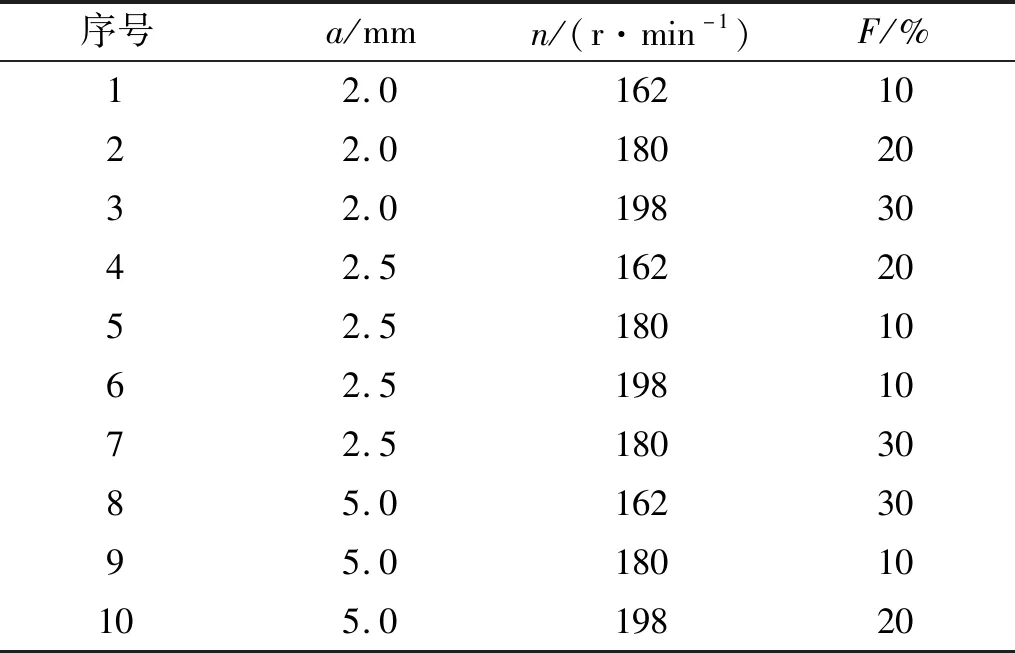
表3 螺杆转子曲面铣削试验方案Tab.3 Experimental plan for screw rotor milling

由正交试验表1可知，需进行10组螺杆转子铣削试验。其中：a为盘铣刀每加工一个截面沿工件Zw方向的位移量；n为盘铣刀转速；F为加工倍率。根据试验方案，测得不同铣削参数下的铣削力试验数据，使用坐标变换式将铣削力投影到刀具坐标下，得到刀具坐标系Oc-XcYcZc下三个方向所受的平均铣削力，如表4所示。

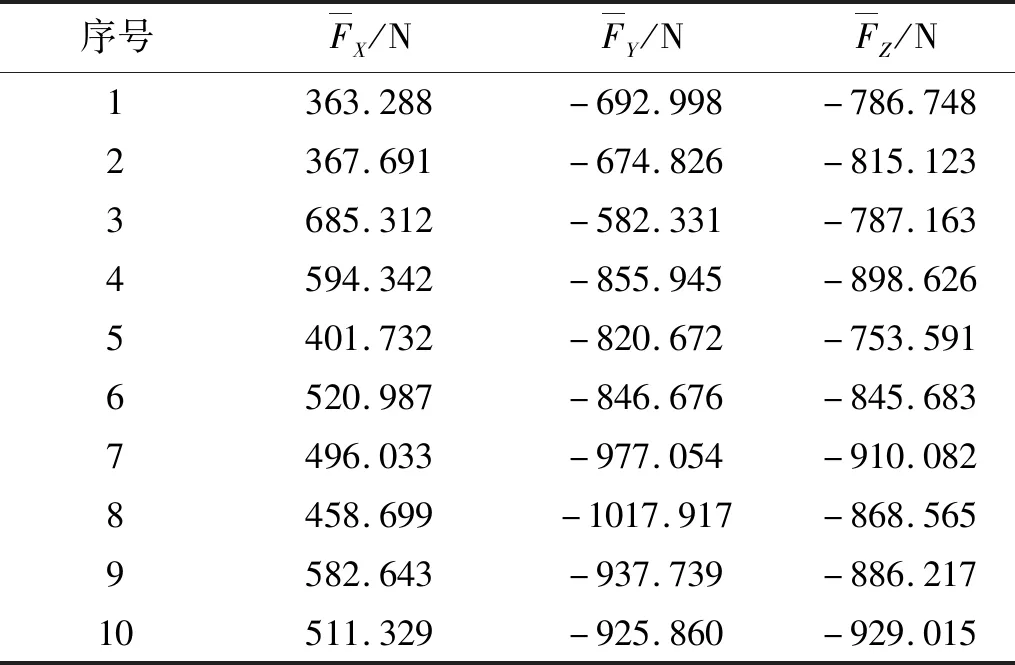
表4 刀具平均切削力Tab.4 Average cutting force of tool

将表4所示的平均铣削力带代入式(19)中，分别计算出中各组铣削参数下的平均铣削力系数如表5所示,系数中的负号表示该方向的铣削力与文中规定的正方向相反。

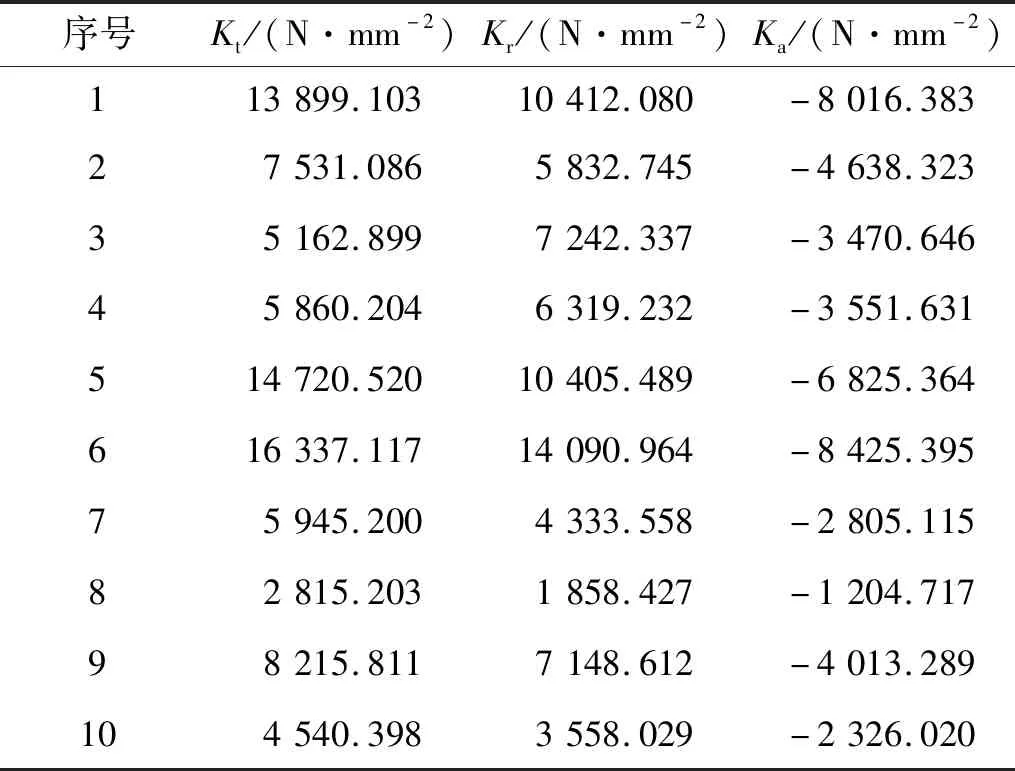
表5 螺杆转子平均铣削力系数计算结果Tab.5 Calculation result of average milling force coefficient of screw rotor

通过多元非线性回归求得切向、径向和轴向的模型，如式(20)、式(21)和式(22)所示

Kt=82 488.861+6 057.801a-745.850n-

1 552.520F-1 040.347a2+2.161n2+28.378F2

(20)

Kr=164 592.802+3 842.936a-1 717.104n-

1 184.012F-722.357a2+4.932n2+22.163F2

(21)

Ka=-84 180.568+995.286a+782.904n+

667.366F-5.972a2-2.212n2-11.324F2

(22)

3 数值求解

3.1 基于隐式Adams方法的数值分析

基于隐式Adams方法的稳定性预测判断流程如图9所示。

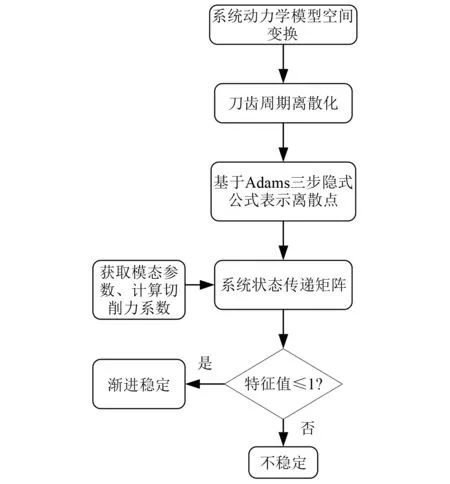
图9 稳定性预测流程图Fig.9 Flow chart of stability prediction

将式(1)进行状态空间变换，令初始时刻为t0，可以通过求解获得

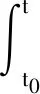
(23)

刀齿周期Tc可以分为两个阶段，自由振动时间间隔tz和强迫振动时间间隔Tc-tz。当刀具处于自由振动时刻t，即t∈[t0,t0+tz]，则可以得到

x(t)=e(A(t-t0))x(t0)

(24)

加工过程中，当刀具处于强迫振动时刻t时，即t∈[t0+tz,Tc]，将强迫振动的切削时间Tc-tz进行离散，平均分成m个时间间隔，则每个时间间隔可以表示为h=(Tc-tz)/m，则相应的离散点可以表示为

ti=t0+tz+(i-1)h,i=1,2,…,m+1

(25)

当t∈[ti,ti+1]时，代入式(23)可以得到

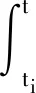
(26)

当i=1时，将式(25)代入式(24)可以得到状态量x(t1)和时滞量x(tm+1-Tc)的关系，如式(27)所示

x(t1)=x(t0+tz)=e(Atz)x(t0)=

e(Atz)x(tm+1-Tc)

(27)

通过隐式Adams方法表示其他离散点，为了简化表达式，将B(ti)表示为Bi，将x(ti)表示为xi，x(ti-Tc)表示为xi-T。

19e(Ah)Bi(xi-xi-T)-5e(2Ah)Bi-1(xi-1-xi-1-T)+

e(3Ah)Bi-2(xi-2-xi-2-T)]

(28)

简化式(28)得到

Hi-2xi-2+Hi-1xi-1+(-e(Ah)+Hi)xi+(I+Hi+1)=
Hi-2xi-2-T+Hi-1xi-1-T+Hixi-T+Hi+1xi+1-T

(29)

联立式(27)和式(29)可得

(30)

其中，

(31)

(32)

通过IAM法求得系统的状态传递矩阵Φ为

Φ=M-1N

(33)

根据Floquet理论，当传递矩阵Φ的特征值等于1时，系统处于稳定边界；当传递矩阵Φ的特征值小于1时，系统处于渐进稳定状态；当传递矩阵Φ的特征值大于1时，系统会进入颤振状态。

3.2 稳定性分析

切向切削力系数、径向切削力系数和轴向切削力系数可通过回归模型式(20)、式(21)和式(22)计算得出。设置切向切削力系数Kt=10 499.441 N/m2，径向切削力系数Kr=7 988.942 N/m2，轴向切削力系数Ka=-2 332.002 N/m2。将模态参数设置为表1中第一行参数，从安全性范围考虑将主轴转速范围设置在常用的加工参数，主轴转速n从150～230 r/min，并设置200个等间距的转速；切削深度ap从0～4 mm，并设置200个等间距切削深度，稳定性叶瓣图构成了200×200的网格。设置离散数m为40，使用计算机软件进行数值仿真结果如图10所示。

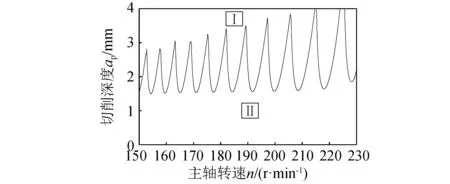
图10 螺杆转子铣削稳定性叶瓣图Fig.10 Milling stability lobe diagram of screw rotor

如图8所示，在稳定性叶瓣图中，曲线以下部分代表稳定区域，即区域Ⅱ，在曲线以上的部分代表不稳定区域，即区域Ⅰ。稳定性叶瓣图中存在多个叶瓣，所有叶瓣的最低点连成线所构成的稳定区域为绝对稳定区域。可以为下一步的切削试验提供依据。

4 铣削试验

为验证本文提出的稳定性预测方法，进行螺杆转子铣削试验。试验所用铣床为LXK300G螺旋槽数控铣床，盘铣刀直径为290 mm。被加工工件材料为45号钢，直径为50 mm，工件通过顶针和三爪卡盘固定，采用三个加速度传感器多点布置，以保证采集振动信号的质量，如图11所示。

图11 试验现场Fig.11 Test site

试验的加工参数为：螺杆为左旋，导程为400 mm，螺旋角为18.511°，出于安全性考虑，主轴转速设定为160 r/min，170 r/min，180 r/min，190 r/min，200 r/min，210 r/min，Zc方向的间歇位移量为常用的加工范围，将其设置为2.0 mm，2.5 mm，3.0 mm，3.5 mm，4.0 mm，4.5 mm，5.0 mm。将间歇位移量经螺旋角转换后得到切削深度如表6所示，将其反映到稳定性叶瓣图中，如图12所示。

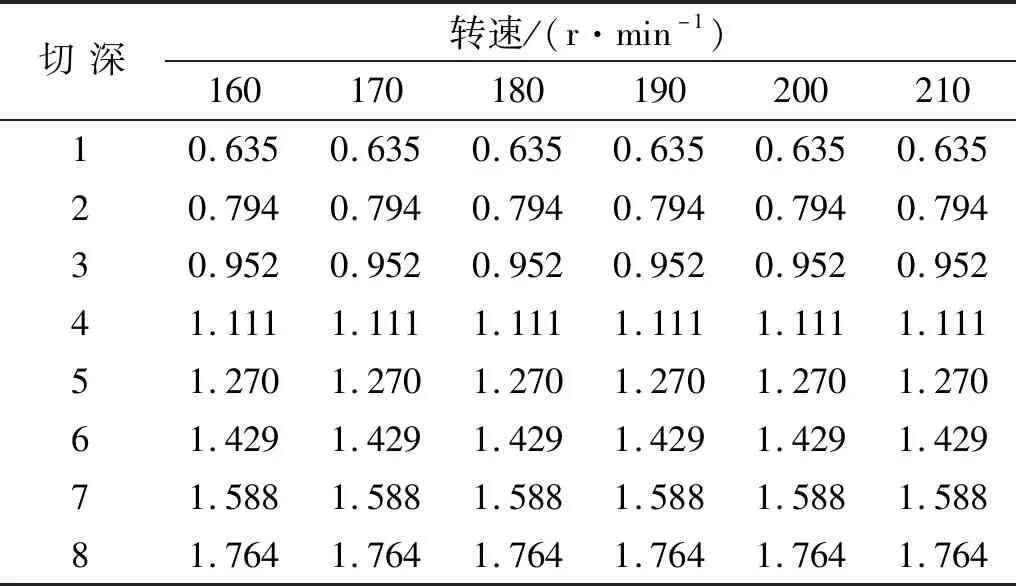
表6 铣削稳定性试验参数Tab.6 Parameters for milling stability experiment

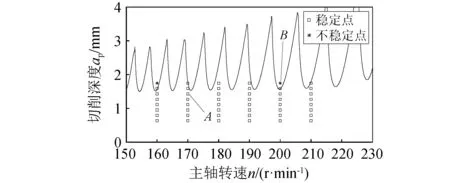
图12 铣削稳定性验证试验参数Fig.12 Experimental parameters for milling stability verification

选取不同的主轴转速和切削深度进行切削，利用DEWE Soft公司的SIRIUS-ACC数据采集器搜集振动信号，并根据统计理论获得不稳定点和稳定点。稳定点A的时域图及频谱图如图13所示。不稳定点B的时域图及频谱图如图14所示。

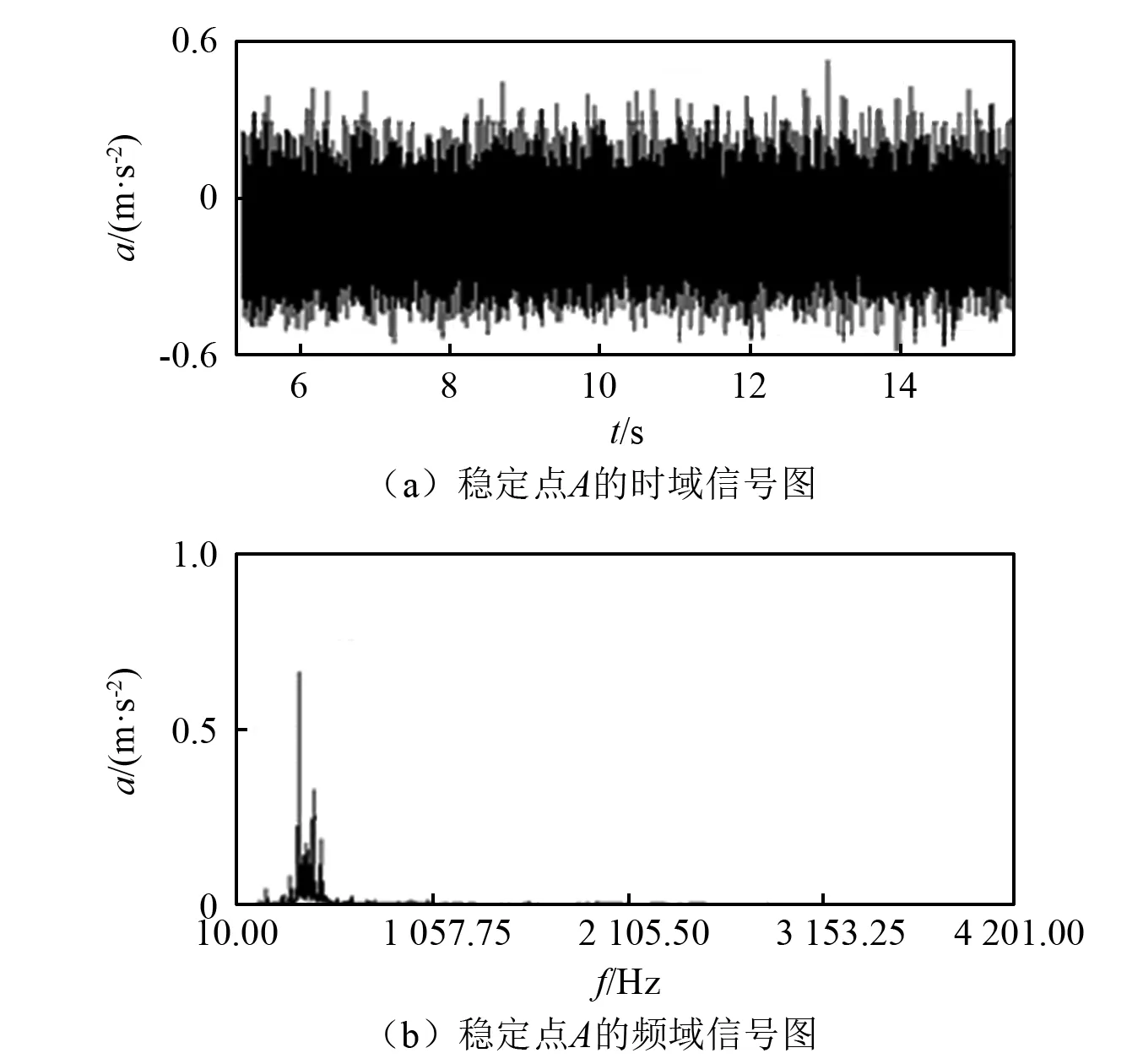
图13 稳定点A的信号图Fig.13 Signal diagram of stable point A

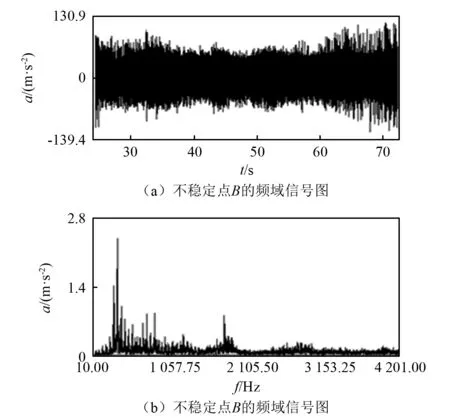
图14 不稳定点B的信号图Fig.14 Signal diagram of unstable point B

由图13和图14可以看出，稳定加工状态和不稳定加工状态时域的振动信号图中幅值相差近200倍，点A和点B的频域特征均存在振动，该振动信号是由于测点布置、工件之间结合部和加工过程盘铣刀径向切入量的变化导致的，除稳定点A和不稳定点B的共同特征外，在不稳定点B的频域信号中存相似明显的颤振频率，表明在螺杆转子铣削过程中存在颤振现象，与解析结果吻合良好。对其他组测试数据分析可以得到类似结果。隐式Adams方法的计算机求解结果和试验结果吻合良好，且适用于三自由度螺旋曲面铣削系统，能够准确的预测切削稳定性。在计算效率方面，与全离散法进行了对比，采用CPU为I5-4200U、内存为12 G的便携式计算机进行计算，取离散度为40，全离散法耗时1 621.010 s，而隐式Adams方法耗时为682.128 s，耗时约为全离散方法的42%。

5 结 论

本文针对螺旋曲面铣削系统在加工过程中产生的振动现象，基于隐式Adams方法来预测螺旋曲面铣削加工过程的稳定性，得到如下结论：

(1)通过分析螺旋曲面加工系统特性，建立了三自由度螺旋曲面铣削系统动力学模型。采用模态试验，利用锤击法获取传递函数幅频特性曲线，并应用导纳圆拟合法提取稳定性预测所需要的模态参数。

(2)提出基于隐式Adams的三自由度螺旋曲面铣削动力学系统稳定性预测方法，并通过铣削试验进行验证。试验结果表明，数值求解结果与试验结果相吻合，即该方法适用于螺旋曲面铣削系统的稳定性预测。